第432场周赛:跳过交替单元格的之字形遍历、机器人可以获得的最大金币数、图的最大边权的最小值、统计 K 次操作以内得到非递减子数组的数目
Q1、跳过交替单元格的之字形遍历
1、题目描述
给你一个 m x n 的二维数组 grid,数组由 正整数 组成。
你的任务是以 之字形 遍历 grid,同时跳过每个 交替 的单元格。
之字形遍历的定义如下:
- 从左上角的单元格
(0, 0)开始。 - 在当前行中向 右 移动,直到到达该行的末尾。
- 下移到下一行,然后在该行中向 左 移动,直到到达该行的开头。
- 继续在行间交替向右和向左移动,直到所有行都被遍历完。
**注意:**在遍历过程中,必须跳过每个 交替 的单元格。
返回一个整数数组 result,其中包含按 顺序 记录的、且跳过交替单元格后的之字形遍历中访问到的单元格值。
2、解题思路
-
方向交替:
- 遍历过程中,偶数行从左到右,奇数行从右到左。可以使用
reverse方法在遍历奇数行时反转数组。
- 遍历过程中,偶数行从左到右,奇数行从右到左。可以使用
-
跳过单元格:
-
通过布尔变量
flag来控制是否访问当前单元格。 -
每访问一个单元格后,将
flag取反,跳过下一个单元格。
-
-
结果记录:
- 将每次访问到的单元格值存入结果数组
ret中。
- 将每次访问到的单元格值存入结果数组
3、代码实现
class Solution {
public:vector<int> zigzagTraversal(vector<vector<int>>& grid) {vector<int> ret; // 存储最终结果数组bool flag = true; // 标记是否访问当前单元格, 初始为访问// 遍历每一行for (int i = 0; i < grid.size(); ++i) {// 当前行的引用, 便于操作auto& row = grid[i];// 奇数行需要反转以实现从右到左的遍历if (i % 2 == 1) {ranges::reverse(row); // 使用 C++20 的 ranges::reverse 反转行}// 遍历当前行的所有元素for (int x : row) {// 如果标记为 true, 则访问当前单元格if (flag) {// 将当前单元格值加入结果数组ret.push_back(x);}// 取反标记, 跳过下一个单元格flag = !flag;}}return ret; // 返回最终结果}
};

4、复杂度分析
时间复杂度分析
- 行遍历:
- 外层
for循环遍历所有m行。
- 外层
- 行内遍历:
- 每行遍历 n 个元素,共访问 m × n m\times n m×n 个单元格。
- 奇数行反转操作的复杂度为
O(n)。
总时间复杂度: O ( m × n ) O(m \times n) O(m×n)
空间复杂度分析
- 额外空间:
- 结果数组
ret存储跳过单元格后的值,大小最多为 ⌈ m × n / 2 ⌉ \lceil m \times n / 2 \rceil ⌈m×n/2⌉。 - 反转操作在原地完成,不需要额外空间。
- 结果数组
总空间复杂度: O ( m × n ) O(m \times n) O(m×n)(存储结果数组的空间)
Q2、机器人可以获得的最大金币数
1、题目描述
给你一个 m x n 的网格。一个机器人从网格的左上角 (0, 0) 出发,目标是到达网格的右下角 (m - 1, n - 1)。在任意时刻,机器人只能向右或向下移动。
网格中的每个单元格包含一个值 coins[i][j]:
- 如果
coins[i][j] >= 0,机器人可以获得该单元格的金币。 - 如果
coins[i][j] < 0,机器人会遇到一个强盗,强盗会抢走该单元格数值的 绝对值 的金币。
机器人有一项特殊能力,可以在行程中 最多感化 2个单元格的强盗,从而防止这些单元格的金币被抢走。
**注意:**机器人的总金币数可以是负数。
返回机器人在路径上可以获得的 最大金币数 。
2、解题思路
我们可以使用动态规划 (Dynamic Programming, DP) 来解决问题。采用一个三维 dp 数组,其中 dp[i][j][k] 表示机器人到达网格单元 (i, j) 时,感化了 k 个强盗后能够获得的最大金币数。
动态规划转移方程
-
定义状态
dp[i][j][k]:到达单元(i, j),感化了k个强盗后的最大金币数。k的范围为[0, 2],表示机器人最多能感化 2 个强盗。
-
状态转移
- 假设当前单元格的金币值为
coins[i][j]:- 如果从 上方
(i-1, j)转移到(i, j):- 如果不感化强盗,
dp[i][j][k] = max(dp[i][j][k], dp[i-1][j][k] + coins[i][j])。 - 如果感化强盗(即
coins[i][j] < 0且剩余感化次数k > 0),dp[i][j][k] = max(dp[i][j][k], dp[i-1][j][k-1])。
- 如果不感化强盗,
- 如果从 左侧
(i, j-1)转移到(i, j):- 与从上方的情况类似。
- 如果从 上方
- 假设当前单元格的金币值为
-
初始条件
- 对于起点
(0, 0):- 如果
coins[0][0] >= 0,金币数为coins[0][0]。 - 如果
coins[0][0] < 0且感化强盗次数k > 0,金币数为0(感化该强盗)。
- 如果
- 对于起点
-
最终结果
-
机器人到达右下角
(m-1, n-1)时,可能感化了 0、1 或 2 个强盗。最终答案为:max(dp[m-1][n-1][0], dp[m-1][n-1][1], dp[m-1][n-1][2])
-
3、代码实现
class Solution {
public:int maximumAmount(vector<vector<int>>& coins) {int m = coins.size(); // 网格的行数int n = coins[0].size(); // 网格的列数// 定义 DP 数组: dp[i][j][k] 表示到达 (i, j) 感化了 k 个强盗后的最大金币数vector<vector<vector<int>>> dp(m, vector<vector<int>>(n, vector<int>(3, INT_MIN)));// 初始化起点for (int k = 0; k <= 2; ++k) {dp[0][0][k] = (coins[0][0] < 0 && k > 0) ? 0 : coins[0][0];}// 动态规划填表for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {// 遍历感化强盗的次数 kfor (int k = 0; k <= 2; ++k) {// 跳过起点if (i == 0 && j == 0) {continue;}int coinValue = coins[i][j]; // 当前单元格的金币值// 从上方到达当前单元格 (i, j)if (i > 0) {if (coinValue >= 0) {// 当前单元格是正值, 直接加金币dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j][k] + coinValue);} else {// 当前单元格是负值, 分两种情况讨论dp[i][j][k] =max(dp[i][j][k], dp[i - 1][j][k] + coinValue); // 不感化强盗if (k > 0) {dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j][k - 1]); // 感化强盗}}}// 从左侧到达当前单元格 (i, j)if (j > 0) {if (coinValue >= 0) {dp[i][j][k] = max(dp[i][j][k], dp[i][j - 1][k] + coinValue);} else {dp[i][j][k] = max(dp[i][j][k], dp[i][j - 1][k] + coinValue);if (k > 0) {dp[i][j][k] = max(dp[i][j][k], dp[i][j - 1][k - 1]);}}}}}}// 返回到达右下角时感化最多 2 个强盗的最大金币数return max({dp[m - 1][n - 1][0], dp[m - 1][n - 1][1], dp[m - 1][n - 1][2]});}
};

4、复杂度分析
时间复杂度
- 三重循环:外层遍历网格的每个单元格,两层内循环遍历感化次数
k,总复杂度为 O ( m × n × 3 ) = O ( m × n ) O(m \times n \times 3) = O(m \times n) O(m×n×3)=O(m×n)。
空间复杂度
- 使用了一个三维数组
dp,大小为 O ( m × n × 3 ) O(m \times n \times 3) O(m×n×3)。
Q3、图的最大边权的最小值
1、题目描述
给你两个整数 n 和 threshold ,同时给你一个 n 个节点的 有向 带权图,节点编号为 0 到 n - 1 。这个图用 二维 整数数组 edges 表示,其中 edges[i] = [Ai, Bi, Wi] 表示节点 Ai 到节点 Bi 之间有一条边权为 Wi的有向边。
你需要从这个图中删除一些边(也可能 不 删除任何边),使得这个图满足以下条件:
- 所有其他节点都可以到达节点 0 。
- 图中剩余边的 最大 边权值尽可能小。
- 每个节点都 至多 有
threshold条出去的边。
请你返回删除必要的边后,最大 边权的 最小值 为多少。如果无法满足所有的条件,请你返回 -1
2、解题思路
本题本质上是一个 图的最短路径问题,但有多个限制条件。我们可以通过以下步骤来思考并解决问题:
-
反向图构建
我们需要从每个节点到达节点0,所以我们构建图的 反向图。反向图中,原本从Ai到Bi的边变为从Bi到Ai的边。这样,我们只需要考虑从节点0到其他节点的路径即可。 -
最大边权最小化
为了确保所有的节点都能到达节点 0,且最大边权最小,我们需要使用 最短路径算法。这里的最短路径的定义是:我们要求路径中的 最大边权最小,这和普通的最短路径问题有些不同。我们可以使用 Dijkstra 算法 来解决这个问题。Dijkstra 算法通常用于找到从起点到所有其他节点的最短路径,而在这个问题中,我们可以将路径的 “最短” 定义为 “最大边权最小”。
-
满足
threshold条件
限制每个节点至多有threshold条出去的边,意味着我们需要在考虑边的同时,保持每个节点的出度不超过threshold。这个限制可以通过构建图时进行检查。 -
最终返回
经过 Dijkstra 算法,我们能够找到从节点 0 到其他所有节点的最大边权。如果所有节点都能到达节点 0,则返回最大边权中的最小值;如果有节点无法到达节点 0,则返回 -1。
3、代码实现
class Solution {
public:int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {// 如果边小于 n-1, 直接返回 -1 (无法构成连通图)if (edges.size() < n - 1) {return -1;}// 构建反向图vector<vector<pair<int, int>>> g(n);// g[y] 包含 (x, w), 表示 x -> y 的边权为 wfor (const auto& edge : edges) {int x = edge[0], y = edge[1], w = edge[2];g[y].emplace_back(x, w);}// 初始化距离数组, 初始时所有节点的距离为正无穷const int INF = numeric_limits<int>::max();vector<int> dis(n, INF);dis[0] = 0; // 起点到自身的最大边权为 0// 最小堆, 存储 (最大边权, 节点编号)priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;pq.emplace(0, 0); // 起点while (!pq.empty()) {auto [d, x] = pq.top();pq.pop();// 如果当前距离大于记录的最小距离, 跳过if (d > dis[x]) {continue;}// 遍历当前节点的所有入边for (const auto& [y, w] : g[x]) {int new_d = max(d, w); // 更新最大边权// 如果找到更优的路径if (new_d < dis[y]) {dis[y] = new_d;pq.emplace(new_d, y);}}}// 找到所有节点到达 0 的最大边权值int ret = *max_element(dis.begin(), dis.end());return ret == INF ? -1 : ret; // 如果节点无法到达, 返回 -1, 否则返回答案}
};

4、复杂度分析
时间复杂度
- 图的构建:
O(E),其中E是边的数量。 - Dijkstra 算法:
O((E + V) log V),其中E是边数,V是节点数。使用优先队列实现 Dijkstra,时间复杂度为O((E + V) log V)。
因此,整体时间复杂度为 O((E + V) log V)。
空间复杂度
- 使用了
O(V + E)的空间来存储图和优先队列。
Q4、统计 K 次操作以内得到非递减子数组的数目
1、题目描述
给你一个长度为 n 的数组 nums 和一个整数 k 。
对于 nums 中的每一个子数组,你可以对它进行 至多 k 次操作。每次操作中,你可以将子数组中的任意一个元素增加 1 。
注意 ,每个子数组都是独立的,也就是说你对一个子数组的修改不会保留到另一个子数组中。
请你返回最多 k 次操作以内,有多少个子数组可以变成 非递减 的。
如果一个数组中的每一个元素都大于等于前一个元素(如果前一个元素存在),那么我们称这个数组是 非递减 的。
2、解题思路
我们需要通过合理的算法找到最多 k 次操作可以使得多少个子数组变为非递减的。对于每一个子数组,考虑以下步骤:
- 单调队列:
- 我们可以通过滑动窗口和单调队列来优化子数组的判断过程。
- 在滑动窗口中,每次考虑将窗口的某一段变成非递减的子数组。
- 修正次数计算:
- 对于每个子数组,我们计算需要多少次操作使得它变为非递减。具体来说,如果
nums[i] > nums[i+1],我们需要进行nums[i] - nums[i+1]次操作才能使得nums[i]小于或等于nums[i+1]。
- 对于每个子数组,我们计算需要多少次操作使得它变为非递减。具体来说,如果
- 左边界和右边界的维护:
- 对于每个子数组,我们维护左右边界,确保在窗口内的操作次数不超过
k。 - 如果窗口内的操作次数超过
k,则我们调整窗口的左边界。
- 对于每个子数组,我们维护左右边界,确保在窗口内的操作次数不超过
- 栈和单调队列的配合:
- 使用栈来维护每个元素的左边界和右边界,栈的作用是帮助我们快速找到某个元素的最近的一个较小元素。
- 单调队列用于保持当前窗口内的元素的单调性,从而帮助我们高效地计算每个子数组的操作次数。
3、代码实现
class Solution {
public:long long countNonDecreasingSubarrays(vector<int>& nums, int k) {int n = nums.size();vector<int> left(n), right(n);vector<int> s = {-1}; // 栈, 初始化为 -1// 构造 left 和 right 数组for (int i = 0; i < n; ++i) {while (s.size() > 1 && nums[i] >= nums[s.back()]) {right[s.back()] = i; // 更新右边界s.pop_back();}left[i] = s.back(); // 栈顶是左侧 > nums[i] 的最近元素s.push_back(i);}for (int i : s) {if (i != -1) {// 栈中剩余元素的右边界为 nright[i] = n;}}// 记录每个 i 右侧有哪些位置的 left 是 ivector<vector<int>> g(n);for (int w = 0; w < n; ++w) {if (left[w] >= 0) {g[left[w]].push_back(w);}}// 滑动窗口 + 单调队列long long ret = 0;// 当前窗口内的修正次数int cnt = 0;// 窗口的左边界int l = 0;// 单调队列, 维护窗口最大值的下标deque<int> q;for (int r = 0; r < n; ++r) {int x = nums[r];// 计算窗口内最大值与当前值的差距if (!q.empty()) {cnt += max(nums[q.front()] - x, 0);}// 单调队列入队, 维持单调性while (!q.empty() && nums[q.back()] <= x) {q.pop_back();}q.push_back(r);// 调整窗口右边界, 直到满足修正次数的限制while (cnt > k) {int out = nums[l];for (int w : g[l]) {if (w > r) {break;}cnt -= (out - nums[w]) * (min(right[w] - 1, r) - w + 1);}++l;// 单调队列出队if (!q.empty() && q.front() < l) {q.pop_front();}}// 计算窗口内的子数组个数ret += r - l + 1;}return ret;}
};

4、复杂度分析
栈的处理:栈的操作复杂度是 O(n)。
滑动窗口和单调队列:每次右边界 r 只会被访问一次,因此整体时间复杂度为 O(n)。
总时间复杂度:由于主要的操作是 O(n),因此整体时间复杂度为 O(n)。
相关文章:

第432场周赛:跳过交替单元格的之字形遍历、机器人可以获得的最大金币数、图的最大边权的最小值、统计 K 次操作以内得到非递减子数组的数目
Q1、跳过交替单元格的之字形遍历 1、题目描述 给你一个 m x n 的二维数组 grid,数组由 正整数 组成。 你的任务是以 之字形 遍历 grid,同时跳过每个 交替 的单元格。 之字形遍历的定义如下: 从左上角的单元格 (0, 0) 开始。在当前行中向…...

RK3399开发板Linux实时性改造
本次测试基于NanoPC-T4开发板(国产化处理器RK3399),4.19.111内核Xenomai实时性改造测试。 Xenomai下载网站:https://xenomai.org/downloads/ NanoPC-T4网站:https://wiki.friendlyarm.com/wiki/index.php/NanoPC-T4/z…...

青少年编程与数学 02-006 前端开发框架VUE 22课题、状态管理
青少年编程与数学 02-006 前端开发框架VUE 22课题、状态管理 一、状态管理二、Vuex1. 安装Vuex2. 创建Vuex Store3. 在Vue应用中使用Store4. 在组件中使用状态5. 模块化Store 三、Vuex应用示例1. 创建项目2. 安装Vuex3. 设置Vuex Store4. 在主项目中使用Store5. 创建组件6. 更新…...

Linux 内核中的 netif_start_queue 函数:启动网络接口发送队列的关键
在 Linux 内核的网络子系统中,netif_start_queue 函数扮演着至关重要的角色。这个函数的主要功能是启动(或启用)网络接口的发送队列,标志着网络接口已经准备好开始发送数据包。本文将深入探讨 netif_start_queue 函数的用途、工作原理以及在实际网络驱动代码中的应用。 函…...

数据结构之顺序结构二叉树(超详解)
文章目录 1 树1.1 树的概念与结构1.2 相关术语1.3 树的表示与运用场景1.3.1 运用场景 2. 二叉树2.1 概念与结构2.1.1 满二叉树2.1.2 完全二叉树 3. 顺序结构二叉树3.1 堆的引入3.1.1 概念与结构 3.2 功能实现3.2.1 堆的结构3.2.2 初始化、销毁 3.3 堆的插入数据3.3.1 向上调整算…...

acwing_5722_十滴水
acwing_5722_十滴水 下面这篇大佬的题解属实是把指针用明白了,可以好好理解一下: 原题解连接:AcWing 5722. 一个简单模拟实现 - AcWing map/unordered_map的用法:见收藏夹 #include<iostream> #include<unordered_map> #incl…...

acwing-3194 最大的矩形
acwing-3194 最大的矩形 这个题程序设计课上有讲过, 平民算法,时间复杂度在 O ( n 2 ) O(n^2) O(n2) // // Created by HUAWEI on 2024/10/28. // #include<iostream>using namespace std;const int Max_size 1e4 20;int N; int h[Max_size];…...
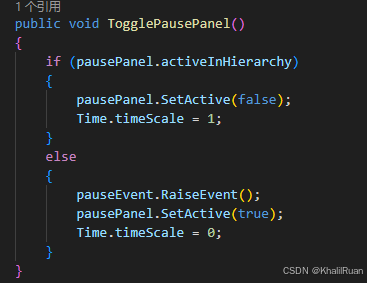
UnityDemo-TheBrave-制作笔记
这是我跟着b站up主MStudio的视频学习制作的,大体上没有去做一些更新的东西,这里只是一个总的总结。在文章的最后,我会放上可以游玩该游戏的链接和exe可执行文件,不过没有对游戏内容进行什么加工,只有基本的功能实现罢了…...

玩转 JMeter:Random Order Controller让测试“乱”出花样
嘿,各位性能测试的小伙伴们!今天咱要来唠唠 JMeter 里超级有趣又超实用的 Random Order Controller(随机顺序控制器),它就像是性能测试这场大戏里的“魔术棒”,轻轻一挥,就能让测试场景变得千变…...

VTK知识学习(33)-交互问题2
1、前言 主要是针对前面有过实现不了交互的情况进行说明,经过一些尝试和分析调用API,总算实现RenderWindowControl函数回调正常串接,当然这个移动处理事件的效果目前也没有确认。 2、使用 vtkImageReslice reslice vtkImageReslice.New();p…...

Centos9-SSH免密登录配置-修改22端口-关闭密码登录-提高安全性
Centos9-SSH免密登录配置-修改22端口-关闭密码登录 生成秘钥对将公钥信息存进authorized_keys测试登录查询访问记录、比对指纹更换22访问端口关闭账号密码登录生成秘钥对 生成密钥对,指定 备注 和 文件目录命令执行后,默认两次回车,不设置秘钥使用密码ssh-keygen -t rsa -b …...

SqlServer: An expression services limit has been reached异常处理
在工作中遇到一个问题,因为项目很老,代码很不规范,出现一种场景: 查询所有客户(5w条以上),然后根据客户Id,再去其他表查询,代码中是直接将customerId拼接到sql中去查询,形成的sql如…...

CentOS下安装Docker
Docker 必须要在Linux环境下才能运行,windows下运行也是安装虚拟机后才能下载安装运行,菜鸟教程 下载安装 linux 依次执行下边步骤 更新 yum yum update 卸载旧的Docker yum remove docker docker-client docker-client-latest docker-common doc…...

WPF控件Grid的布局和C1FlexGrid的多选应用
使用 Grid.Column和Grid.Row布局,将多个C1FlexGrid布局其中,使用各种事件来达到所需效果,点击复选框可以加载数据到列表,移除列表的数据,自动取消复选框等 移除复选框的要注意!!!&am…...

Jenkins-持续集成、交付、构建、部署、测试
Jenkins-持续集成、交付、构建、部署、测试 一: Jenkins 介绍1> Jenkins 概念2> Jenkins 目的3> Jenkins 特性4> Jenkins 作用 二:Jenkins 版本三:DevOps流程简述1> 持续集成(Continuous Integration,CI࿰…...

高级第一次作业
1、shell 脚本写出检测 /tmp/size.log 文件如果存在显示它的内容,不存在则创建一个文件将创建时间写入。 2、写一个 shel1 脚本,实现批量添加 20个用户,用户名为user01-20,密码为user 后面跟5个随机字符。 3、编写个shel 脚本将/usr/local 日录下大于10M的文件转移到…...

Copula算法原理和R语言股市收益率相依性可视化分析
阅读全文:http://tecdat.cn/?p6193 copula是将多变量分布函数与其边缘分布函数耦合的函数,通常称为边缘。在本视频中,我们通过可视化的方式直观地介绍了Copula函数,并通过R软件应用于金融时间序列数据来理解它(点击文…...

反弹SHELL不回显带外正反向连接防火墙出入站文件下载
什么是反弹shell 正向连接正向连接(Forward Connection):正向连接是一种常见的网络通信模式,其中客户端主动发起连接到服务器或目标系统。正向连接通常用于客户端-服务器通信,客户端主动请求服务或资源,例如…...

后盾人JS--JS值类型使用
章节介绍与类型判断 看看构造函数 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</t…...

1月11日
[WUSTCTF2020]CV Maker 可以看到有个注册页面,尝试注册一个用户登进去看看 进来后第一眼就看到文件上传,尝试上传,上传php后返回了 文件上传后端检测exif_imagetype()函数 他提示不是image,也就是需要我们构造一个文件头为图像类…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...
