C++滑动窗口技术深度解析:核心原理、高效实现与高阶应用实践
目录
一、滑动窗口的核心原理
二、滑动窗口的两种类型
1. 固定大小的窗口
2. 可变大小的窗口
三、实现细节与关键点
1. 窗口的初始化
2. 窗口的移动策略
3. 结果的更新时机
四、经典问题与代码示例
示例 1:和 ≥ target 的最短子数组(可变窗口)
示例 2:无重复字符的最长子串(哈希表辅助)
五、边界条件与易错点
1. 数组越界
2. 初始值的设置
3. 哈希表的使用
4. 循环条件错误
六、时间复杂度分析
七、滑动窗口的适用场景
八、滑动窗口的扩展
1. 结合前缀和
2. 结合单调队列
总结
一、滑动窗口的核心原理
滑动窗口(Sliding Window) 是一种基于 双指针(Two Pointers) 的算法设计范式,核心思想是通过维护一个 动态窗口区间([left, right]),在遍历过程中调整窗口的左右边界,避免重复计算,从而将时间复杂度优化到 O(n)。
-
核心逻辑:
-
窗口扩张:
right指针向右移动,扩大窗口,直到满足某个条件。 -
窗口收缩:一旦满足条件,
left指针向右移动,缩小窗口,直到不满足条件。 -
更新结果:在窗口调整过程中,记录最优解。
-
二、滑动窗口的两种类型
1. 固定大小的窗口
-
特点:窗口长度固定为
k,通过滑动窗口的起始位置遍历所有可能的子区间。 -
典型问题:
-
求长度为
k的子数组的最大平均值 -
长度为
k的子字符串的排列匹配
-
C++ 代码模板:
int fixedWindow(vector<int>& nums, int k)
{int sum = 0, max_sum = 0;// 初始化窗口for (int i = 0; i < k; ++i) sum += nums[i];max_sum = sum;// 滑动窗口for (int right = k; right < nums.size(); ++right) {sum += nums[right] - nums[right - k]; // 窗口右移,更新和max_sum = max(max_sum, sum);}return max_sum;
}2. 可变大小的窗口
-
特点:窗口大小不固定,根据问题条件动态调整
left和right指针。 -
典型问题:
-
无重复字符的最长子字符串
-
和大于等于
target的最短子数组
-
C++ 代码模板:
int variableWindow(string s)
{unordered_map<char, int> window;int left = 0, max_len = 0;for (int right = 0; right < s.size(); ++right) {char c = s[right];window[c]++; // 窗口扩张// 窗口收缩条件:出现重复字符while (window[c] > 1) {char d = s[left];window[d]--; // 移出左边界字符left++;}max_len = max(max_len, right - left + 1); // 更新结果}return max_len;
}三、实现细节与关键点
1. 窗口的初始化
-
初始指针位置:通常
left = right = 0。 -
状态变量:如窗口内的和(
sum)、哈希表(记录字符频率)等。
2. 窗口的移动策略
-
扩张条件:一般通过
for循环逐步移动right。 -
收缩条件:在满足特定条件时,通过
while循环移动left,直到条件不满足。
3. 结果的更新时机
-
固定窗口:每次窗口滑动后更新结果。
-
可变窗口:在窗口收缩后或扩张过程中更新结果。
四、经典问题与代码示例
示例 1:和 ≥ target 的最短子数组(可变窗口)
int minSubArrayLen(int target, vector<int>& nums)
{int left = 0, sum = 0;int min_len = INT_MAX;for (int right = 0; right < nums.size(); ++right) {sum += nums[right]; // 窗口扩张while (sum >= target) { // 窗口收缩条件min_len = min(min_len, right - left + 1);sum -= nums[left++]; // 窗口收缩}}return min_len == INT_MAX ? 0 : min_len;
}示例 2:无重复字符的最长子串(哈希表辅助)
int lengthOfLongestSubstring(string s)
{unordered_map<char, int> last_pos; // 记录字符最后出现的位置int left = 0, max_len = 0;for (int right = 0; right < s.size(); ++right) {char c = s[right];// 若字符 c 已存在且在窗口内,移动 left 到 last_pos[c] + 1if (last_pos.count(c) && last_pos[c] >= left) {left = last_pos[c] + 1;}last_pos[c] = right; // 更新字符位置max_len = max(max_len, right - left + 1);}return max_len;
}五、边界条件与易错点
1. 数组越界
-
在固定窗口中,需确保
right - k >= 0。 -
在可变窗口中,需检查
left是否超过right。
2. 初始值的设置
-
最小值初始化为
INT_MAX,最大值初始化为INT_MIN。
3. 哈希表的使用
-
在字符频率统计中,需确保哈希表的键存在性(如用
count()检查)。
4. 循环条件错误
-
错误:在收缩窗口时使用
if而非while,导致窗口未完全收缩。 -
正确:使用
while循环确保窗口收缩到条件不满足。
六、时间复杂度分析
-
固定窗口:O(n),每个元素被访问一次。
-
可变窗口:O(n),每个元素最多被
left和right各访问一次。
七、滑动窗口的适用场景
-
连续子数组/子字符串问题
-
最短/最长满足条件的子数组
-
子数组的和/乘积/频率统计
-
-
优化暴力解法
-
将 O(n²) 的暴力枚举优化为 O(n)
-
-
数据流处理
-
实时处理数据流中的窗口统计量(如移动平均值)
-
八、滑动窗口的扩展
1. 结合前缀和
-
用于处理负数数组或更复杂的条件(如子数组和为
k)。 -
示例代码:
int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> prefix_sum; // 前缀和 -> 出现次数prefix_sum[0] = 1;int sum = 0, count = 0;for (int num : nums) {sum += num;if (prefix_sum.count(sum - k)) {count += prefix_sum[sum - k];}prefix_sum[sum]++;}return count; }
2. 结合单调队列
-
用于维护窗口内的最大值/最小值(如滑动窗口最大值问题)。
-
示例代码:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {deque<int> dq; // 存储下标,按值单调递减vector<int> res;for (int i = 0; i < nums.size(); ++i) {// 移除超出窗口的元素if (!dq.empty() && dq.front() == i - k) dq.pop_front();// 维护单调队列while (!dq.empty() && nums[i] >= nums[dq.back()]) dq.pop_back();dq.push_back(i);// 记录窗口最大值if (i >= k - 1) res.push_back(nums[dq.front()]);}return res; }
总结
滑动窗口的核心在于 双指针的协同移动 和 窗口状态的动态维护。掌握以下要点:
-
明确窗口的 扩张与收缩条件。
-
合理选择 数据结构(如哈希表、单调队列)维护窗口状态。
-
注意 边界条件 和 初始值设置。
-
灵活结合其他算法(如前缀和、单调队列)解决复杂问题。
相关文章:

C++滑动窗口技术深度解析:核心原理、高效实现与高阶应用实践
目录 一、滑动窗口的核心原理 二、滑动窗口的两种类型 1. 固定大小的窗口 2. 可变大小的窗口 三、实现细节与关键点 1. 窗口的初始化 2. 窗口的移动策略 3. 结果的更新时机 四、经典问题与代码示例 示例 1:和 ≥ target 的最短子数组(可变窗口…...

基于构件的软件开发方法
摘要: 本人在2023年1月参与广东某公司委托我司开发的“虚拟电厂”项目,主要负责整体架构设计和中间件的选型,该项目为新型电力存储、电力调度、能源交易提供一整套的软件系统,包括设备接入、负载预测、邀约竞价、用户设备调控等功能。本项目以“虚拟电厂”项目为例,讨论基…...

网站快速收录:如何设置robots.txt文件?
本文转自:百万收录网 原文链接:https://www.baiwanshoulu.com/34.html 为了网站快速收录而合理设置robots.txt文件,需要遵循一定的规则和最佳实践。robots.txt文件是一个纯文本文件,它告诉搜索引擎爬虫哪些页面可以访问ÿ…...
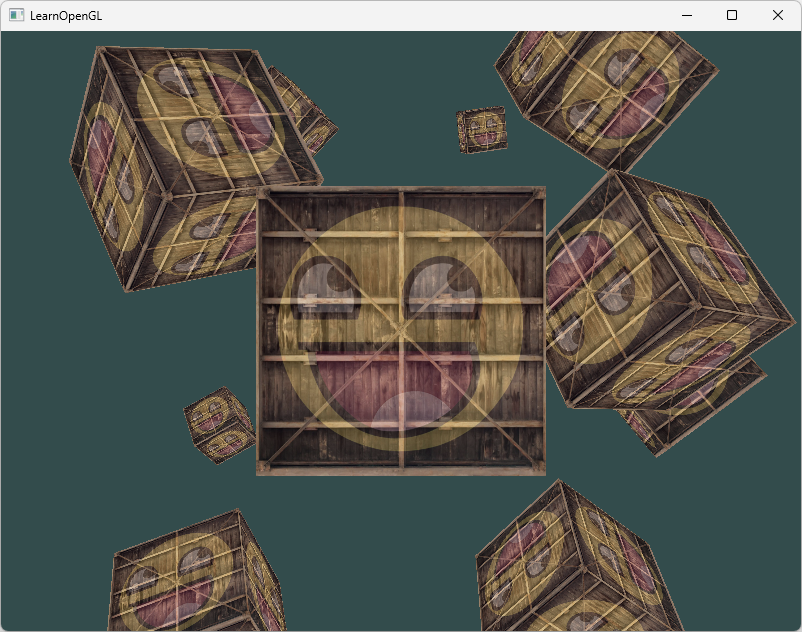
OpenGL学习笔记(六):Transformations 变换(变换矩阵、坐标系统、GLM库应用)
文章目录 向量变换使用GLM变换(缩放、旋转、位移)将变换矩阵传递给着色器坐标系统与MVP矩阵三维变换绘制3D立方体 & 深度测试(Z-buffer)练习1——更多立方体 现在我们已经知道了如何创建一个物体、着色、加入纹理。但它们都还…...

8.攻防世界Web_php_wrong_nginx_config
进入题目页面如下 尝试弱口令密码登录 一直显示网站建设中,尝试无果,查看源码也没有什么特别漏洞存在 用Kali中的dirsearch扫描根目录试试 命令: dirsearch -u http://61.147.171.105:53736/ -e* 登录文件便是刚才登录的界面打开robots.txt…...

【优先算法】专题——位运算
在讲解位运算之前我们来总结一下常见的位运算 一、常见的位运算 1.基础为运算 << &:有0就是0 >> |:有1就是1 ~ ^:相同为0,相异位1 /无进位相加 2.给一个数 n,确定它的二进制表示…...

qt.qpa.plugin: Could not find the Qt platform plugin “dxcb“ in ““
个人博客地址:qt.qpa.plugin: Could not find the Qt platform plugin "dxcb" in "" | 一张假钞的真实世界 我遇到的场景是,在Deepin系统终端中运行PySide应用时,没有错误提示,但在VS Code中运行时ÿ…...

1-刷力扣问题记录
25.1.19 1.size()和.length()有什么区别 2.result.push_back({nums[i], nums[left], nums[right]});为什么用大括号? 使用大括号 {} 是 C11 引入的 初始化列表 语法,它允许我们在构造或初始化对象时直接传入一组值。大括号的使用在许多情况下都能让代码…...

物联网 STM32【源代码形式-使用以太网】连接OneNet IOT从云产品开发到底层MQTT实现,APP控制 【保姆级零基础搭建】
物联网(IoT)是指通过各种信息传感器、射频识别技术、全球定位系统、红外感应器等装置与技术,实时采集并连接任何需要监控、连接、互动的物体或过程,实现对物品和过程的智能化感知、识别和管理。物联网的核心功能包括数据采集与监…...
)
【单层神经网络】基于MXNet的线性回归实现(底层实现)
写在前面 基于亚马逊的MXNet库本专栏是对李沐博士的《动手学深度学习》的笔记,仅用于分享个人学习思考以下是本专栏所需的环境(放进一个environment.yml,然后用conda虚拟环境统一配置即可)刚开始先从普通的寻优算法开始ÿ…...

unity中的动画混合树
为什么需要动画混合树,动画混合树有什么作用? 在Unity中,动画混合树(Animation Blend Tree)是一种用于管理和混合多个动画状态的工具,包括1D和2D两种类型,以下是其作用及使用必要性的介绍&…...

《基于deepseek R1开源大模型的电子数据取证技术发展研究》
《基于deepseek R1开源大模型的电子数据取证技术发展研究》 摘要 本文探讨了基于deepseek R1开源大模型的电子数据取证技术发展前景。随着人工智能技术的快速发展,AI大模型在电子数据取证领域的应用潜力日益凸显。本研究首先分析了电子数据取证的现状和挑战…...

Potplayer常用快捷键
Potplayer是一个非常好用的播放器,功能强大 功能快捷键播放/暂停空格键退出Esc下一帧F上一帧D快进10秒→快退10秒←快进30秒Ctrl →快退30秒Ctrl ←快进1分钟Alt →快退1分钟Alt ←增加播放速度C减少播放速度X恢复正常速度Z增加音量↑减少音量↓静音M显示/隐藏字幕Ctrl A…...

C++ Primer 自定义数据结构
欢迎阅读我的 【CPrimer】专栏 专栏简介:本专栏主要面向C初学者,解释C的一些基本概念和基础语言特性,涉及C标准库的用法,面向对象特性,泛型特性高级用法。通过使用标准库中定义的抽象设施,使你更加适应高级…...

35.Word:公积金管理中心文员小谢【37】
目录 Word1.docx Word2.docx Word2.docx 注意本套题还是与上一套存在不同之处 Word1.docx 布局样式的应用设计页眉页脚位置在水平/垂直方向上均相对于外边距居中排列:格式→大小对话框→位置→水平/垂直 按下表所列要求将原文中的手动纯文本编号分别替换…...

北京钟鼓楼:立春“鞭春牛”,钟鼓迎春来
仁风导和气,勾芒御昊春。“钟鼓迎春”立春鞭春牛民俗体验活动于立春当日在北京钟鼓楼隆重举办。此次活动由北京市钟鼓楼文物保管所主办,京睿文(北京)文化科技有限公司承办,通过礼官报春、击鼓鸣钟、春娃喊春、中国时间文化角色巡游、鞭春牛等一系列精彩的活动环节,为观众呈现了…...

股票入门知识
股票入门(更适合中国宝宝体制) 股市基础知识 本文介绍了股票的基础知识,股票的分类,各板块发行上市条件,股票代码,交易时间,交易规则,炒股术语,影响股价的因素…...

Java自定义IO密集型和CPU密集型线程池
文章目录 前言线程池各类场景描述常见场景案例设计思路公共类自定义工厂类-MyThreadFactory自定义拒绝策略-RejectedExecutionHandlerFactory自定义阻塞队列-TaskQueue(实现 核心线程->最大线程数->队列) 场景1:CPU密集型场景思路&…...

Git的安装步骤详解(复杂的安装界面该如何勾选?)
目录 一、下载与安装 1.官网下载git 2、下载完成之后,双击下载好的exe文件进行安装 3、选择Git的安装路径 4、选择在安装 Git 时要包含的组件和功能 5、选择 Git 快捷方式在 Windows 开始菜单中的位置。 6、选择 Git 使用的默认编辑器 7、调整新仓库中初始分…...

文本预处理
一、文本的基本单位 1、Token 定义:文本的最小单位,例如单词、标点符号。 示例: 原句: "I love NLP." 分词结果: [I, love, NLP, .] 2、语法与语义 语法:词的结构和句子的组合规则。 语义&a…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...
