一学就会:A*算法详细介绍(Python)
📢本篇文章是博主人工智能学习以及算法研究时,用于个人学习、研究或者欣赏使用,并基于博主对相关等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在👉启发式算法专栏:
【人工智能】- 【启发式算法】(6)---《一学就会:A*算法详细介绍(Python)》
一学就会:A*算法详细介绍(Python)
目录
A*算法介绍
A*算法的核心概念
A*算法的特点
A*算法示例:迷宫
执行步骤
第1步:初始化
第2步:扩展当前节点(起始节点)
第3步:选择下一个节点(最低 f(n))
第4步:处理当前节点 (0,1)
第5步:继续探索
重点说明
最终结果
A*算法与其他相关算法的比较
[Python] A*算法实现
[Results] 运行结果
[Notice] 注意事项
适用场景
实现建议
A*算法介绍
A*算法是一种高效的路径搜索算法,广泛应用于人工智能、机器人技术、游戏开发等领域。它由Peter Hart、Nils Nilsson和Bertram Raphael于1968年首次提出。A算法结合了Dijkstra算法的系统性搜索和启发式搜索的优点,通过使用启发式函数来减少搜索空间,同时保证找到最短路径。
A*算法的核心概念
A*算法是一种最佳优先搜索算法,它通过以下三个关键函数来评估路径:
-
g(n):从起点到当前节点的实际代价。
-
h(n):从当前节点到目标节点的启发式估算代价。
-
f(n) = g(n) + h(n):通过当前节点到达目标的总估算代价。
在每次迭代中,A*算法会选择具有最低f(n)值的节点进行扩展,并更新其邻居节点的代价。如果邻居节点的试探性代价低于之前记录的值,则会更新该节点的代价,并将其添加到开放集合中。这一过程会持续进行,直到找到目标节点或确定路径不存在。
A*算法的特点
-
最优性:当使用可接受的启发式函数时,A*算法能够找到最短路径。
-
效率:启发式函数的引导使得A*算法比Dijkstra算法探索更少的节点。
-
灵活性:启发式函数可以根据不同场景进行定制。
-
完整性:如果存在解决方案,A*算法将找到它。
A*算法示例:迷宫
以下是使用A*算法在一个示例迷宫中寻找路径的详细步骤说明:
假设有以下10x10的迷宫:
S 0 0 0 0 0 0 0 0 0
0 1 1 0 1 1 0 1 1 0
0 1 0 0 0 0 0 0 1 0
0 1 1 1 1 1 0 1 1 0
0 0 0 0 1 0 0 0 0 0
0 1 1 0 1 1 1 1 1 0
0 1 0 0 0 0 0 0 0 0
0 1 1 1 1 1 1 1 1 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 E其中,S 表示起点 (0,0),E 表示终点 (9,9),0 表示可以通行的路径,1 表示障碍物.
执行步骤
第1步:初始化
-
起始节点:
(0,0),初始化其g(n)=0,h(n)由直线距离计算,f(n)=0+13.416=13.416。 -
开放列表:未被选择的节点。
-
封闭列表:已被选择的节点。
-
当前节点:起始节点。
第2步:扩展当前节点(起始节点)
-
邻节点:
(0,1),(1,0)。 -
检查范围:确保邻节点在迷宫范围内。
-
障碍物检查:
(0,1)是0,(1,0)是0。 -
计算邻节点
g(n):-
(0,1):起始节点的g(n)=0+1=1。 -
(1,0):起始节点的g(n)=0+1=1。
-
-
计算邻节点
h(n):-
(0,1)的h(n)=sqrt((9-0)^2 + (9-1)^2)= sqrt(81+64)=11.401。 -
(1,0)的h(n)=sqrt((9-1)^2 + (9-0)^2)=sqrt(64+81)=11.401。
-
-
计算邻节点
f(n):-
(0,1)的f(n)=1+11.401=12.401。 -
(1,0)的f(n)=1+11.401=12.401。
-
-
在开放列表中添加邻节点:
-
(0,1)和(1,0)添加到开放列表。
-
第3步:选择下一个节点(最低 f(n))
开放列表中有 (0,1) 和 (1,0),它们的 f(n) 都是 12.401。可以选择其中任意一个:
选择 (0,1) 作为当前节点。
第4步:处理当前节点 (0,1)
-
邻节点:
(0,0)(起点,已在封闭列表),(0,2),(1,1)。 -
障碍物检查:
-
(0,2)是0。 -
(1,1)是1(障碍物)。
-
-
生成有效邻节点:
(0,2)。 -
计算
(0,2)的g(n):-
来自
(0,1),g(n)=1+1=2。
-
-
计算
(0,2)的h(n):-
sqrt((9-0)^2 + (9-2)^2)= sqrt(81+49)=10.630。
-
-
计算
(0,2)的f(n):-
2+10.630=12.630。
-
-
将
(0,2)添加到开放列表:-
开放列表现在包含
(1,0), (0,2)。
-
第5步:继续探索
重复步骤,选择开放列表中 f(n) 最低的节点,继续扩展并更新邻节点的 g(h,f) 值,直到到达目标节点 (9,9)。
重点说明
-
扩展当前节点:每次从开放列表中取出
f(n)最低的节点,生成其邻节点。 -
更新邻节点信息:
-
如果邻节点未被访问过,计算其
g(h,f)并加入开放列表。 -
如果邻节点已在开放列表中,需要比较新的
g(n)是否更小。如果更小,更新父节点和g(n)。
-
-
终止条件:
-
当前节点是目标节点,回溯路径。
-
开放列表为空,没有路径。
-
最终结果
经过反复的节点扩展和评估,A* 算法最终找到从起点 (0,0) 到终点 (9,9) 的最短路径。路径将避免迷宫中的所有障碍物,确保每一步都是经过成本最低的选择。
A*算法与其他相关算法的比较
| 算法 | 与A*的关系 | 关键差异 | 优缺点 |
|---|---|---|---|
| Dijkstra算法 | A*是Dijkstra算法的扩展 | A*使用f(n)=g(n)+h(n),Dijkstra仅使用g(n) | A*在有启发式函数时性能更好,Dijkstra无需启发式函数 |
| Bellman-Ford算法 | 基于边的松弛 | Bellman-Ford支持负边权重,A*通常更快 | Bellman-Ford适用于有负权重的图,A*需要启发式函数 |
| Floyd-Warshall算法 | 解决所有点对最短路径问题 | Floyd-Warshall使用动态规划,A*是增量搜索 | Floyd-Warshall适合密集图,A*适合实时路径搜索 |
[Python] A*算法实现
项目代码我已经放入下面链接里面:🔥
A*算法实现
若是下面代码复现困难或者有问题,也欢迎评论区留言。
"""《A*算法实现》时间:2025.02.27环境:迷宫作者:不去幼儿园
"""
import heapq
import matplotlib.pyplot as plt
import numpy as npclass Node:"""节点类表示搜索树中的每一个点。"""def __init__(self, parent=None, position=None):self.parent = parent # 该节点的父节点self.position = position # 节点在迷宫中的坐标位置self.g = 0 # G值:从起点到当前节点的成本self.h = 0 # H值:当前节点到目标点的估计成本self.f = 0 # F值:G值与H值的和,即节点的总评估成本# 比较两个节点位置是否相同def __eq__(self, other):return self.position == other.position# 定义小于操作,以便在优先队列中进行比较def __lt__(self, other):return self.f < other.fdef astar(maze, start, end):"""A*算法实现,用于在迷宫中找到从起点到终点的最短路径。"""start_node = Node(None, start) # 创建起始节点end_node = Node(None, end) # 创建终点节点open_list = [] # 开放列表用于存储待访问的节点closed_list = [] # 封闭列表用于存储已访问的节点heapq.heappush(open_list, (start_node.f, start_node)) # 将起始节点添加到开放列表while open_list:current_node = heapq.heappop(open_list)[1] # 弹出并返回开放列表中 f 值最小的节点closed_list.append(current_node) # 将当前节点添加到封闭列表if current_node == end_node: # 如果当前节点是目标节点,则回溯路径path = []while current_node:path.append(current_node.position)current_node = current_node.parentreturn path[::-1] # 返回反向路径,即从起点到终点的路径(x, y) = current_node.positionneighbors = [(x-1, y), (x+1, y), (x, y-1), (x, y+1)] # 获取当前节点周围的相邻节点for next in neighbors:if 0 <= next[0] < maze.shape[0] and 0 <= next[1] < maze.shape[1]: # 确保相邻节点在迷宫范围内if maze[next[0], next[1]] == 1: # 如果相邻节点是障碍物,跳过continueneighbor = Node(current_node, next) # 创建相邻节点if neighbor in closed_list: # 如果相邻节点已在封闭列表中,跳过不处理continueneighbor.g = current_node.g + 1 # 计算相邻节点的 G 值neighbor.h = ((end_node.position[0] - next[0]) ** 2) + ((end_node.position[1] - next[1]) ** 2) # 计算 H 值neighbor.f = neighbor.g + neighbor.h # 计算 F 值if add_to_open(open_list, neighbor): # 如果相邻节点的新 F 值较小,则将其添加到开放列表heapq.heappush(open_list, (neighbor.f, neighbor))return None # 如果没有找到路径,返回 Nonedef add_to_open(open_list, neighbor):"""检查并添加节点到开放列表。"""for node in open_list:if neighbor == node[1] and neighbor.g > node[1].g:return Falsereturn True # 如果不存在,则返回 True 以便添加该节点到开放列表def visualize_path(maze, path, start, end):"""将找到的路径可视化在迷宫上。"""maze_copy = np.array(maze)for step in path:maze_copy[step] = 0.5 # 标记路径上的点plt.figure(figsize=(10, 10))plt.imshow(maze_copy, cmap='hot', interpolation='nearest')path_x = [p[1] for p in path] # 列坐标path_y = [p[0] for p in path] # 行坐标plt.plot(path_x, path_y, color='orange', linewidth=2)start_x, start_y = start[1], start[0]end_x, end_y = end[1], end[0]plt.scatter([start_x], [start_y], color='green', s=100, label='Start', zorder=5) # 起点为绿色圆点plt.scatter([end_x], [end_y], color='red', s=100, label='End', zorder=5) # 终点为红色圆点plt.legend()plt.show()# 设定迷宫的尺寸
maze_size = 100
maze = np.zeros((maze_size, maze_size))
obstacle_blocks = [(10, 10, 20, 20), # (y起始, x起始, 高度, 宽度)(30, 40, 20, 30),(60, 20, 15, 10),(80, 50, 10, 45),
]
for y_start, x_start, height, width in obstacle_blocks:maze[y_start:y_start+height, x_start:x_start+width] = 1
start = (0, 0)
end = (92, 93)
maze[start] = 0
maze[end] = 0
path = astar(maze, start, end)
if path:print("路径已找到:", path)visualize_path(maze, path, start, end)
else:print("没有找到路径。")[Results] 运行结果
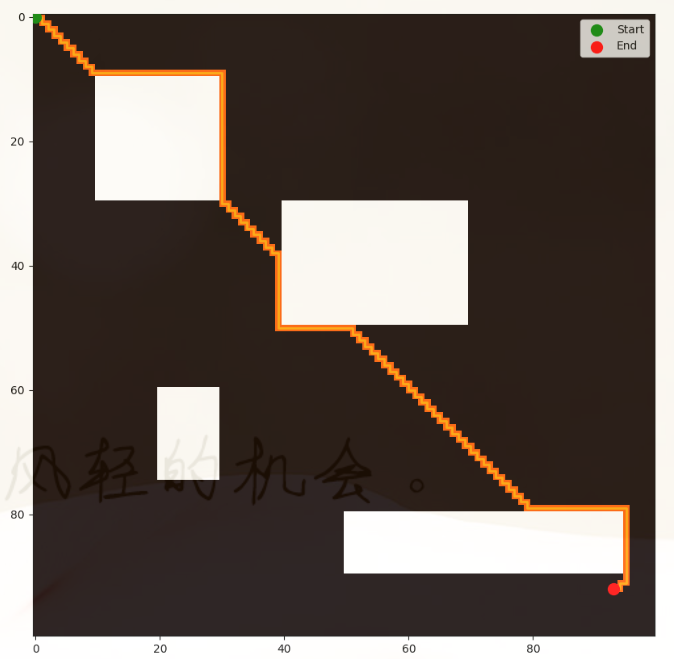
[Notice] 注意事项
# 环境配置
Python 3.11.5
torch 2.1.0
torchvision 0.16.0
gym 0.26.2由于博文主要为了介绍相关算法的原理和应用的方法,缺乏对于实际效果的关注,算法可能在上述环境中的效果不佳或者无法运行,一是算法不适配上述环境,二是算法未调参和优化,三是没有呈现完整的代码,四是等等。上述代码用于了解和学习算法足够了,但若是想直接将上面代码应用于实际项目中,还需要进行修改。
适用场景
A*算法最适合以下场景:
-
单源单目标路径搜索。
-
可以提供领域特定的启发式函数。
-
需要最优解。
-
有足够的内存来维护开放/关闭集合。
主要应用场景
-
迷宫寻路:在游戏开发中,A*算法可以用来为游戏角色找到从起点到终点的最短路径,例如在迷宫类游戏中,角色需要绕过障碍物尽快到达目标。
-
机器人路径规划:在机器人领域,A*算法可用于规划机器人在复杂环境中的移动路径,帮助其避开障碍物并找到到达目标位置的最佳路线。
-
地图导航:在 GPS 导航系统或地图应用中,A*算法可以计算两点之间的最短路径,考虑道路长度、交通状况等多种因素,为用户提供最优的行驶路线建议。
实现建议
-
使用优先队列(如二叉堆或斐波那契堆)快速选择节点。
-
根据图的大小选择合适的数据结构。
-
设计并验证有效的启发式函数。
算法优点
-
寻找最短路径:无论是二维平面还是三维空间,A*算法都能够有效地在复杂的环境图中找到从起点到终点的最短路径,尤其是在具有障碍物和多重路径选择的情况下。
-
优化效率:相比传统的广度优先搜索和深度优先搜索,A*算法通过结合启发式估计和实际路径成本,能够更高效地探索可能的路径,减少不必要的计算,大大提升了路径寻找的效率。
-
适应复杂环境:A*算法能够灵活地处理各种环境变化,如新增障碍物、改变目标位置等,只需重新计算路径即可,无需对整个地图进行重新规划。
实现效果
-
准确性:A*算法能够精确地找到最优路径,确保路径的总成本(如距离、时间等)最小,对于大多数场景来说,其结果都是全局最优的。
-
实时性:在处理复杂地图时,A*算法能够在较短时间内完成路径规划,满足实时性要求,特别是在一些动态环境(如即时战略游戏或动态交通导航)中。
-
可视化:通过可视化工具,可以清晰地看到 A*算法的搜索过程,路径是如何被逐步探索和确定的,这对于调试和理解算法的工作原理非常有帮助。
更多启发式算法文章,请前往:【启发式算法】专栏
博客都是给自己看的笔记,如有误导深表抱歉。文章若有不当和不正确之处,还望理解与指出。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请联系博主删除。如有错误、疑问和侵权,欢迎评论留言联系作者,或者添加VX:Rainbook_2,联系作者。✨
相关文章:

一学就会:A*算法详细介绍(Python)
📢本篇文章是博主人工智能学习以及算法研究时,用于个人学习、研究或者欣赏使用,并基于博主对相关等领域的一些理解而记录的学习摘录和笔记,若有不当和侵权之处,指出后将会立即改正,还望谅解。文章分类在&am…...
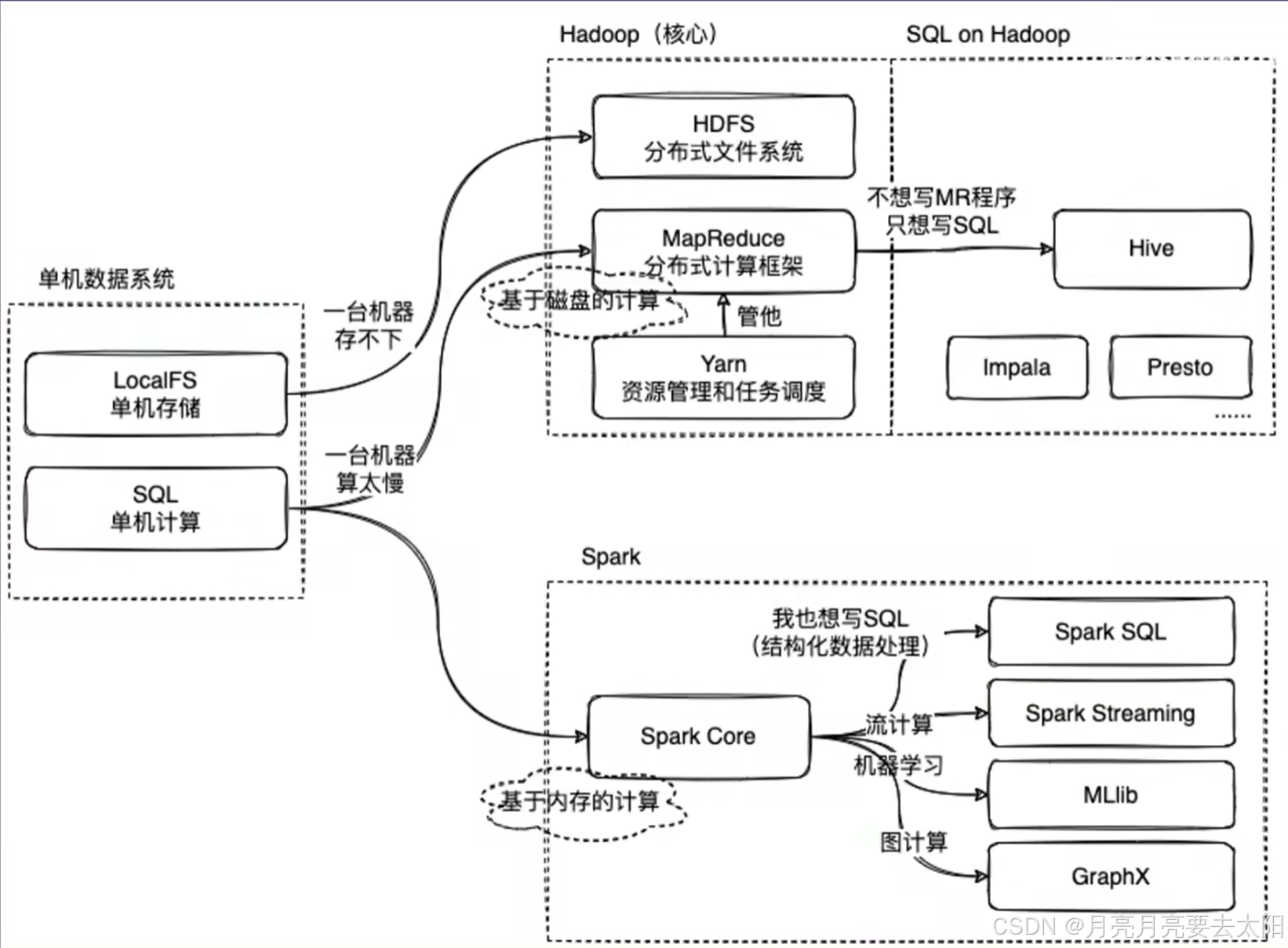
Hadoop、Hive、Spark的关系
Part1:Hadoop、Hive、Spark关系概览 1、MapReduce on Hadoop 和spark都是数据计算框架,一般认为spark的速度比MR快2-3倍。 2、mapreduce是数据计算的过程,map将一个任务分成多个小任务,reduce的部分将结果汇总之后返回。 3、HIv…...

Excel·VBA江西省预算一体化工资表一键处理
每月制作工资表导出为Excel后都需要调整格式,删除0数据的列、对工资表项目进行排序、打印设置等等,有些单位还分有“行政”、“事业”2个工资表就需要操作2次。显然,这种重复操作的问题,可以使用VBA代码解决 目录 代码使用说明1&a…...
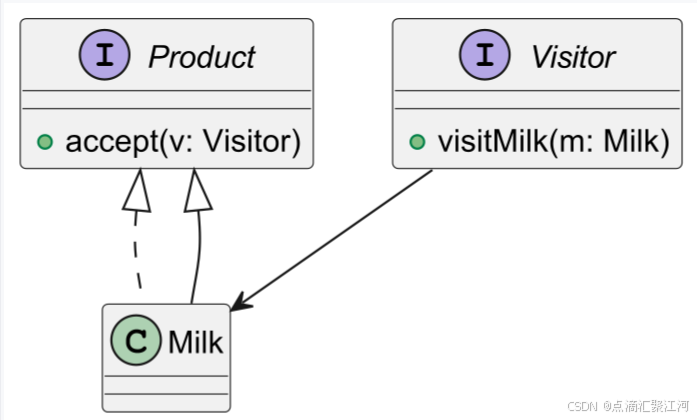
23种设计模式简介
一、创建型(5种) 1.工厂方法 总店定义制作流程,分店各自实现特色披萨(北京店-烤鸭披萨,上海店-蟹粉披萨) 2.抽象工厂 套餐工厂(家庭装含大披萨薯条,情侣装含双拼披萨红酒&#…...

python fire 库与 sys.argv 处理命令行参数
fire库 Python Fire 由Google开发,它使得命令行接口(CLI)的创建变得容易。使用Python Fire,可以将Python对象(如类、函数或字典)转换为可以从终端运行的命令行工具。这能够以一种简单而直观的方式与你的Py…...

PDF处理控件Aspose.PDF,如何实现企业级PDF处理
PDF处理为何成为开发者的“隐形雷区”? “手动调整200页PDF目录耗时3天,扫描件文字识别错误导致数据混乱,跨平台渲染格式崩坏引发客户投诉……” 作为开发者,你是否也在为PDF处理的复杂细节消耗大量精力?Aspose.PDF凭…...
Spring(1)——mvc概念,部分常用注解
1、什么是Spring Web MVC? Spring MVC 是一种基于 Java 的实现了 MVC(Model-View-Controller,模型 - 视图 - 控制器)设计模式的 Web 应用框架,它是 Spring 框架的一个重要组成部分,用于构建 Web 应用程序。…...
C语言(23)
字符串函数 11.strstr函数 1.1函数介绍: 头文件:string.h char *strstr ( const char * str1,const char *str2); 作用:在一个字符串(str1)中寻找另外一个字符串(str2)是否出现过 如果找到…...
Immich自托管服务的本地化部署与随时随地安全便捷在线访问数据
文章目录 前言1.关于Immich2.安装Docker3.本地部署Immich4.Immich体验5.安装cpolar内网穿透6.创建远程链接公网地址7.使用固定公网地址远程访问 前言 小伙伴们,你们好呀!今天要给大家揭秘一个超炫的技能——如何把自家电脑变成私人云相册,并…...
基于SpringBoot的在线付费问答系统设计与实现(源码+SQL脚本+LW+部署讲解等)
专注于大学生项目实战开发,讲解,毕业答疑辅导,欢迎高校老师/同行前辈交流合作✌。 技术范围:SpringBoot、Vue、SSM、HLMT、小程序、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、安卓app、大数据、物联网、机器学习等设计与开发。 主要内容:…...

【Linux】信号处理以及补充知识
目录 一、信号被处理的时机: 1、理解: 2、内核态与用户态: 1、概念: 2、重谈地址空间: 3、处理时机: 补充知识: 1、sigaction: 2、函数重入: 3、volatile&…...

pandas——to_datatime用法
Pandas中pd.to_datetime的用法及示例 pd.to_datetime 是 Pandas 库中用于将字符串、整数或列表转换为日期时间(datetime)对象的核心函数。它在处理时间序列数据时至关重要,能够灵活解析多种日期格式并统一为标准时间类型。以下是其核心用法及…...

《DataWorks 深度洞察:量子机器学习重塑深度学习架构,决胜复杂数据战场》
在数字化浪潮汹涌澎湃的当下,大数据已然成为推动各行业发展的核心动力。身处这一时代洪流,企业对数据的处理与分析能力,直接关乎其竞争力的高低。阿里巴巴的DataWorks作为大数据领域的扛鼎之作,凭借强大的数据处理与分析能力&…...

Java 大视界 -- 基于 Java 的大数据实时数据处理框架性能评测与选型建议(121)
💖亲爱的朋友们,热烈欢迎来到 青云交的博客!能与诸位在此相逢,我倍感荣幸。在这飞速更迭的时代,我们都渴望一方心灵净土,而 我的博客 正是这样温暖的所在。这里为你呈上趣味与实用兼具的知识,也…...

多线程-JUC
简介 juc,java.util.concurrent包的简称,java1.5时引入。juc中提供了一系列的工具,可以更好地支持高并发任务 juc中提供的工具 可重入锁 ReentrantLock 可重入锁:ReentrantLock,可重入是指当一个线程获取到锁之后&…...

DeepSeek:中国AGI先锋,用技术重塑通用人工智能的未来
在ChatGPT掀起全球大模型热潮的背景下,中国AI领域涌现出一批极具创新力的技术公司,深度求索(DeepSeek)便是其中的典型代表。这家以“探索未知、拓展智能边界”为使命的AI企业,凭借长文本理解、逻辑推理与多模态技术的…...

Vue 框架深度解析:源码分析与实现原理详解
文章目录 一、Vue 核心架构设计1.1 整体架构流程图1.2 模块职责划分 二、响应式系统源码解析2.1 核心类关系图2.2 核心源码分析2.2.1 数据劫持实现2.2.2 依赖收集过程 三、虚拟DOM与Diff算法实现3.1 Diff算法流程图3.2 核心Diff源码 四、模板编译全流程剖析4.1 编译流程图4.2 编…...

Python爬虫获取淘宝快递费接口的详细指南
在电商运营中,快递费用的透明化和精准计算对于提升用户体验、优化物流成本以及增强市场竞争力至关重要。淘宝提供的 item_fee 接口能够帮助开发者快速获取商品的快递费用信息。本文将详细介绍如何使用 Python 爬虫技术结合 item_fee 接口,实现高效的数据…...

基于BMO磁性细菌优化的WSN网络最优节点部署算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 无线传感器网络(Wireless Sensor Network, WSN)由大量分布式传感器节点组成,用于监测物理或环境状况。节点部署是 WSN 的关键问…...

Android Activity的启动器ActivityStarter入口
Activity启动器入口 Android的Activity的启动入口是在ActivityStarter类的execute(),在该方法里面继续调用executeRequest(Request request) ,相应的参数都设置在方法参数request中。代码挺长,分段现在看下它的实现,分段一&#x…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
