平衡二叉树(AVL树)
平衡二叉树是啥我就不多说了,本篇博客只讲原理与方法。
首先引入平衡因子的概念。平衡因子(Balance Factor),以下简称bf。
bf = 右子树深度 - 左子树深度。平衡结点的平衡因子可为:-1,0,1。除此之外的结点都需要调整。
如下图:

AVL树的基础创建
创建AVL树的基本架构与二叉搜索树的创建基本一样,不同是为了方便后续的旋转与平衡因子的改变,多引入bf与parent记录结点的平衡因子与该结点的父节点,形成三叉链。

AVL树的旋转
右单旋
新节点插入较高左子树的左侧

以上过程可以简单的看作是30的右子树变成60的左子树,60变成30的右子树。其中h高度可以取值为0。

这是两种不同的情况。不同点在于30的右子树为NULL,此时并不需要更新其子树的parent结点的指向。每个结点的bf统统归零。
左单旋
新节点插入较高右子树的右侧

以上过程可简单看成,60的左变成30的右,30变成60的左。其中60的左可以为空。

和右单旋同理。
先左单旋再右单旋(LR)
新节点插入较高左子树的右侧

路径可以形象的看作“<”先左后右(LR)
将双旋变成单旋后再旋转,即:先对30进行左单旋,然后再对90进行右单旋,旋转完成后再
考虑平衡因子的更新。
平衡因子的更新
情况一:如上图在b处插入后60结点的bf=-1,最终平衡树的平衡因子为60:0,30:0,90:1。
情况二:
在c处插入后60结点的bf=1,最终平衡因子为30:-1,60:0,90:0。
情况三:
插入60结点,60结点bf=1,最终平衡因子为30:0,60:0,90:0。
先右单旋再左单旋(RL)
新节点插入较高右子树的左侧
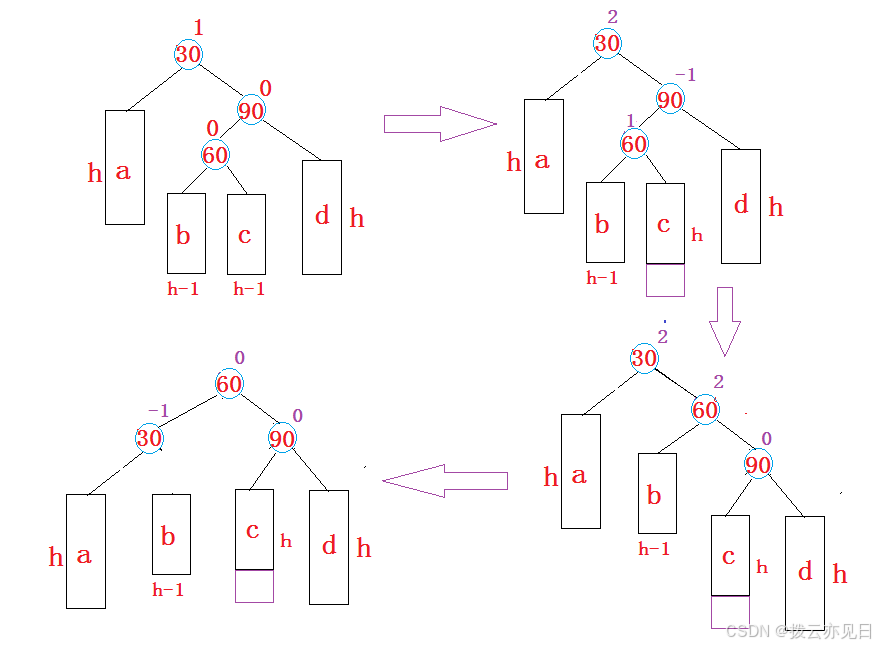
路径可以形象看作“>’,先右后左(RL)。
将双旋变成单旋后再旋转,即:先对90进行左单旋,然后再对30进行右单旋,旋转完成后再
考虑平衡因子的更新。
平衡因子讨论和LR类似。
代码
#pragma once
#include <iostream>
#include <stdlib.h>
using namespace std;template <class K,class V>
struct AVLtreeNode {AVLtreeNode<K, V>* _right;AVLtreeNode<K, V>* _left;AVLtreeNode<K, V>* _parent;AVLtreeNode(const pair<K,V>& kv):_right(nullptr),_left(nullptr),_parent(nullptr),_kv(kv),_bf(0){}int _bf; //平衡因子pair<K, V> _kv;
};
template <class K,class V>
class AVLtree {typedef AVLtreeNode<K,V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}while (parent){if (cur == parent->_right){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 0){//不影响break;}else if (parent->_bf == 1 || parent->_bf == -1){//高度变了,需要继续向上计算平衡因子cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//parnet所在的子树出现不平衡,需要旋转if (parent->_bf == 2){if (cur->_bf == 1){RotateL(parent);}else if (cur->_bf == -1){RotateRL(parent);}}else if (parent->_bf == -2){if (cur->_bf == -1){RotateR(parent);}else if(cur->_bf==1){RotateLR(parent);}}break;}}return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) subRL->_parent = parent;subR->_left = parent;Node* node = parent->_parent;parent->_parent = subR;//1、原来parent是这棵树的根,现在subR是根//2、parent不是根,parent还有他自己的_parent,现在让_parent指向subRif (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (node->_left == parent){node->_left = subR;}else{node->_right = subR;}subR->_parent = node;}parent->_bf = subR->_bf = 0;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subL->_right;Node* node = parent->_parent;subL->_right = parent;if (subLR) subLR->_parent = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parent == node->_left){node->_left = subL;}else{node->_right = subL;}subL->_parent = node;}subL->_bf = parent->_bf = 0;}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 1){subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == 0){subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first <<" : " << root->_kv.second << endl;_InOrder(root->_right);}void InOrder(){_InOrder(_root);cout << endl;}int Height(Node* root){if (root == nullptr) return 0;int left = Height(root->_left);int right = Height(root->_right);return left > right ? left + 1 : right + 1;}bool _IsBalance(Node*root){if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return abs(leftHeight - rightHeight) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);}bool IsBalance(){return _IsBalance(_root);}private:Node* _root=nullptr;
};void TestAVLTree()
{int a[] = { 16,3,7,11,9,26,18,14,15 };AVLtree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrder();cout << t.IsBalance() << endl;
}相关文章:

平衡二叉树(AVL树)
平衡二叉树是啥我就不多说了,本篇博客只讲原理与方法。 首先引入平衡因子的概念。平衡因子(Balance Factor),以下简称bf。 bf 右子树深度 - 左子树深度。平衡结点的平衡因子可为:-1,0,1。除此…...
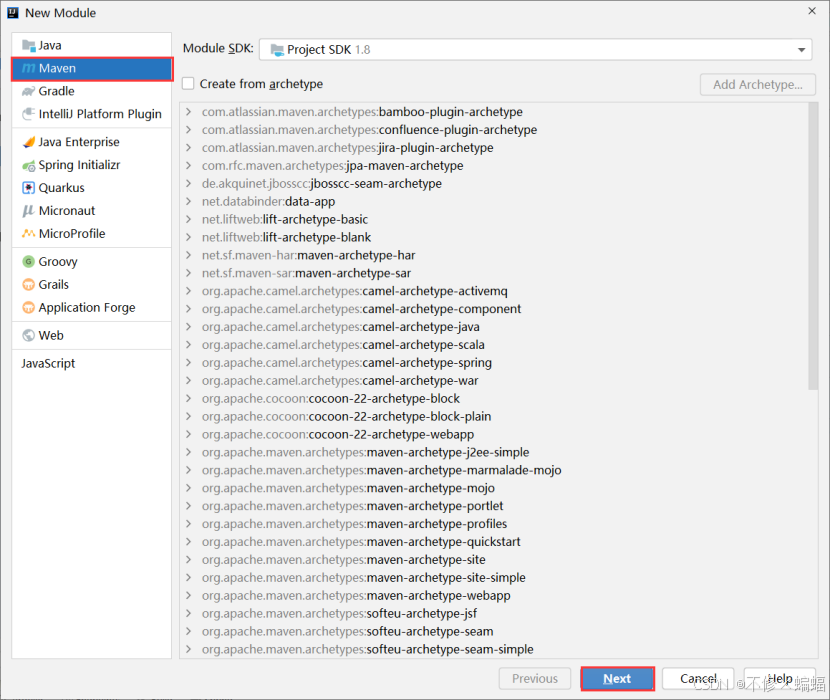
SpringBoot(一)--搭建架构5种方法
目录 一、⭐Idea从spring官网下载打开 2021版本idea 1.打开创建项目 2.修改pom.xml文件里的版本号 2017版本idea 二、从spring官网下载再用idea打开 三、Idea从阿里云的官网下载打开 编辑 四、Maven项目改造成springboot项目 五、从阿里云官网下载再用idea打开 Spri…...
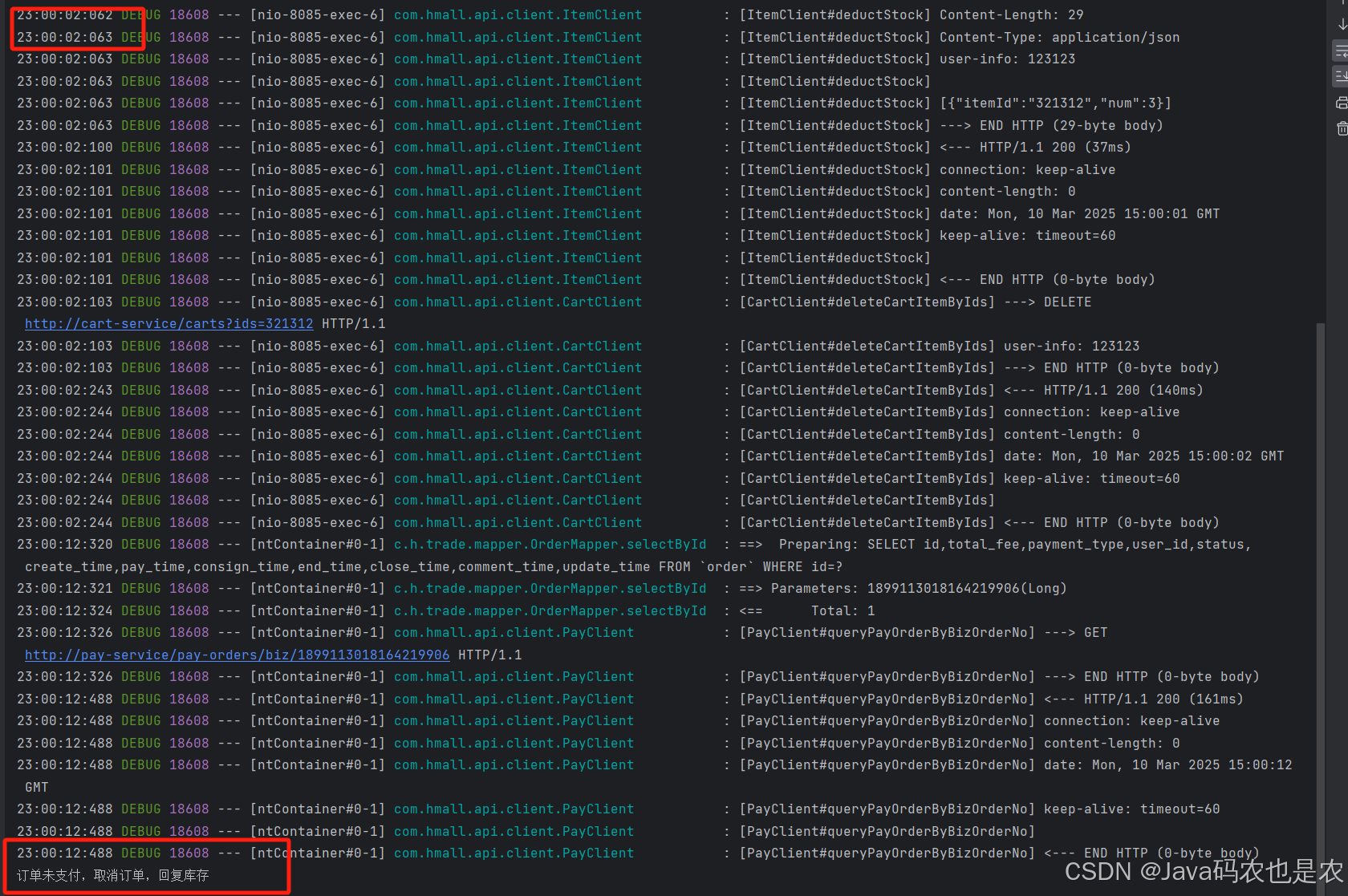
RabbitMQ使用延迟消息
RabbitMQ使用延迟消息 1.什么情况下使用延迟消息 延迟消息适用于需要在一段时间后执行某些操作的场景,常见的有以下几类: 1.1. 订单超时取消(未支付自动取消) 场景: 用户下单后,如果 30 分钟内未付款&a…...

MyBatis-Plus 分页查询接口返回值问题剖析
在使用 MyBatis-Plus 进行分页查询时,很多开发者会遇到一个常见的问题:当分页查询接口返回值定义为 Page<T> 时,执行查询会抛出异常;而将返回值修改为 IPage<T> 时,分页查询却能正常工作。本文将从 MyBatis-Plus 的分页机制入手,详细分析这一问题的根源,并提…...

DeepLabv3+改进7:在主干网络中添加SegNext_Attention|助力涨点
🔥【DeepLabv3+改进专栏!探索语义分割新高度】 🌟 你是否在为图像分割的精度与效率发愁? 📢 本专栏重磅推出: ✅ 独家改进策略:融合注意力机制、轻量化设计与多尺度优化 ✅ 即插即用模块:ASPP+升级、解码器 PS:订阅专栏提供完整代码 论文简介 近期有关移动网络设计…...
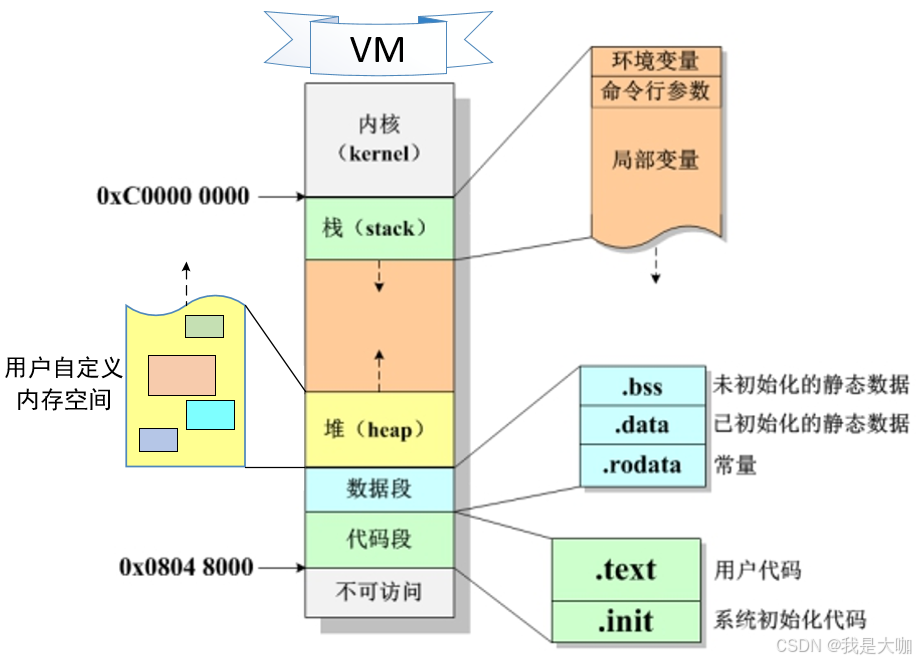
c语言笔记 内存管理之栈内存
物理内存和虚拟内存 在c语言的程序需要内存资源,用来存放变量,常量,函数代码等,不同的内容存放在不同的内存区域,不同的内存区域有着不同的特征。 c语言的每一个进程都有着一片结构相同的 虚拟内存,虚拟内…...

分布式事务的原理
文章目录 基于 XA 协议的两阶段提交(2PC)三阶段提交(3PC)TCC(Try-Confirm-Cancel)Saga 模式消息队列(可靠消息最终一致性) 分布式事务是指在分布式系统中,涉及多个节点或…...

鸿基智启:东土科技为具身智能时代构建确定性底座
人类文明的每一次跨越都伴随着工具的革新。从蒸汽机的齿轮到计算机的代码,生产力的进化始终与技术的“具身化”紧密相连。当大语言模型掀起认知革命,具身智能正以“物理实体自主决策”的双重属性重新定义工业、医疗、服务等领域的运行逻辑。在这场革命中…...

SQL29 计算用户的平均次日留存率
SQL29 计算用户的平均次日留存率 计算用户的平均次日留存率_牛客题霸_牛客网 题目:现在运营想要查看用户在某天刷题后第二天还会再来刷题的留存率。 示例:question_practice_detail -- 输入: DROP TABLE IF EXISTS question_practice_detai…...

MWC 2025 | 移远通信推出AI智能无人零售解决方案,以“动态视觉+边缘计算”引领智能零售新潮流
在无人零售市场蓬勃发展的浪潮中,自动售货机正经历着从传统机械式操作向AI视觉技术的重大跨越。 移远通信作为全球领先的物联网整体解决方案供应商,精准把握行业趋势,在2025世界移动通信大会(MWC)上宣布推出全新AI智能…...

sparkTTS window 安装
下载 Spark-TTS Go to Spark-TTS GitHubClick "Code" > "Download ZIP", then extract it. 2. 建立 Conda 环境 conda create -n sparktts python3.12 -y conda activate sparktts 3. Install Dependencies pip install -r requirements.txt In…...

数据库原理6
1.数据是信息的载体 2.数据库应用程序人员的主要职责:编写应用系统的程序模块 3.关系规范化理论主要属于数据库理论的研究范畴 4.数据库主要有检索和修改(包括插入,删除,更新)两大操作 5.概念模型又称为语义模型。…...

接口自动化入门 —— Http的请求头,请求体,响应码解析!
在接口自动化测试中,HTTP请求头、请求体和响应码是核心组成部分。理解它们的作用、格式和解析方法对于进行有效的接口测试至关重要。以下是详细解析: 1. HTTP 请求头(Request Header) 1.1 作用 请求头是客户端向服务器发送的附加…...

tcc编译器教程6 进一步学习编译gmake源代码
本文以编译gmake为例讲解如何使用tcc进行复杂一点的c代码的编译 1 简介 前面主要讲解了如何编译lua解释器,lua解释器的编译很简单也很容易理解.当然大部分c语言程序编译没那么简单,下面对前面的gmake程序进行编译. 2 gmake源码结构 首先打开之前tcc-busybox-for-win32\gmak…...

公司共享网盘怎么建立
公司共享网盘的建立,关键在于明确使用需求、选择合适的网盘服务、搭建统一的文件管理规范、做好权限分级与安全防护。尤其要强调选择合适的网盘服务这一点,如果企业规模较大,且对协同办公的需求强烈,就需要考虑支持多人实时协作、…...

【高分论文密码】AI大模型和R语言的全类型科研图形绘制,从画图、标注、改图、美化、组合、排序分解科研绘图每个步骤
在科研成果竞争日益激烈的当下,「一图胜千言」已成为高水平SCI期刊的硬性门槛——数据显示很多情况的拒稿与图表质量直接相关。科研人员普遍面临的工具效率低、设计规范缺失、多维数据呈现难等痛点,因此科研绘图已成为成果撰写中的至关重要的一个环节&am…...

深入理解Java中的static关键字及其内存原理
static是Java中实现类级共享资源的核心修饰符,它突破了对象实例化的限制,使得变量和方法能够直接与类本身绑定。这种特性让static成为构建工具类、全局配置等场景的利器,但同时也带来独特的内存管理机制需要开发者关注。 static修饰成员变量…...

linux 系统 之centos安装 docker
对于 CentOS 安装 Docker 的前置条件 首先,需要安装一些必要的软件包, 对于 CentOS 7,可以使用以下命令: sudo yum install -y yum-utils device-mapper-persistent-data lvm2添加 Docker 仓库 设置 Docker 的官方仓库。对于 …...

Python语法核心架构与核心知识点:从理论到实践
一、Python的核心设计哲学 Python以“简洁优雅”为核心理念,遵循以下原则: # Zen of Python(输入 import this 可查看) >>> import this The Zen of Python, by Tim Peters ... Simple is better than complex. Readab…...

FreeRTOS(5)内核控制函数及其他函数
FreeRTOS 提供了一些用于控制内核的 API 函数,这些 API 函数主要包含了进出临界区、开关中断、启停任务调度器等一系列用于控制内核的 API 函数。本章就来学习 FreeRTOS 的内 核控制函数。 内核控制函数 1. 函数 taskYIELD() 此函数用于请求切换任务, …...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
