31-判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。 进阶: 如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
方法一:双指针法
双指针法是一种直观且高效的方法,通过分别使用两个指针遍历字符串 s 和 t,比较对应字符,若匹配则移动 s 的指针,无论是否匹配都移动 t 的指针,最后判断 s 的指针是否到达末尾。
function isSubsequence(s: string, t: string): boolean {let i = 0;let j = 0;while (i < s.length && j < t.length) {if (s[i] === t[j]) {i++;}j++;}return i === s.length;
}
复杂度分析
- 时间复杂度:(O(n)),其中 n 是字符串
t的长度。因为只需要遍历一次字符串t。 - 空间复杂度:(O(1)),只使用了常数级的额外空间,用于存储两个指针。
方法二:递归法
递归法通过不断缩小问题规模,比较当前字符是否相等,若相等则递归判断剩余部分,若不相等则只递归处理 t 的剩余部分,直到 s 为空或者 t 为空。
function isSubsequence(s: string, t: string): boolean {if (s.length === 0) {return true;}if (t.length === 0) {return false;}if (s[0] === t[0]) {return isSubsequence(s.slice(1), t.slice(1));}return isSubsequence(s, t.slice(1));
}
复杂度分析
- 时间复杂度:(O(n)),其中 n 是字符串
t的长度。在最坏情况下,每次递归调用都会处理t的一个字符。 - 空间复杂度:(O(n)),主要是递归调用栈的空间开销,递归深度最大为
t的长度。
方法三:动态规划法
动态规划法通过构建一个二维数组 dp 来记录子问题的解,dp[i][j] 表示 s 的前 i 个字符是否是 t 的前 j 个字符的子序列,根据字符是否相等进行状态转移。
function isSubsequence(s: string, t: string): boolean {const m = s.length;const n = t.length;const dp: boolean[][] = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(false));for (let j = 0; j <= n; j++) {dp[0][j] = true;}for (let i = 1; i <= m; i++) {for (let j = 1; j <= n; j++) {if (s[i - 1] === t[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = dp[i][j - 1];}}}return dp[m][n];
}
复杂度分析
- 时间复杂度:(O(m * n)),其中 m 是字符串
s的长度,n 是字符串t的长度。需要填充一个 (m+1) 行 (n+1) 列的二维数组。 - 空间复杂度:(O(m * n)),主要用于存储二维数组
dp。
进阶问题思路
当有大量输入的 S(如 S1, S2, ... , Sk 其中 (k >= 10) 亿)需要依次检查它们是否为 T 的子序列时,双指针法的时间复杂度会很高,因为每次都要重新遍历 T。可以使用预处理 T 的方法,记录每个字符在 T 中出现的所有位置,然后对于每个输入的 S,使用二分查找来快速定位字符在 T 中的位置,这样可以将每次判断的时间复杂度降低到 (O(m * log n)),其中 m 是 S 的长度,n 是 T 的长度。以下是实现代码:
function preprocess(t: string): number[][] {const pos: number[][] = new Array(26).fill(0).map(() => []);for (let i = 0; i < t.length; i++) {const index = t.charCodeAt(i) - 'a'.charCodeAt(0);pos[index].push(i);}return pos;
}function isSubsequenceAdvanced(s: string, t: string, pos: number[][]): boolean {let prev = -1;for (let i = 0; i < s.length; i++) {const index = s.charCodeAt(i) - 'a'.charCodeAt(0);const charPos = pos[index];let left = 0;let right = charPos.length - 1;let found = false;while (left <= right) {const mid = Math.floor((left + right) / 2);if (charPos[mid] > prev) {right = mid - 1;prev = charPos[mid];found = true;} else {left = mid + 1;}}if (!found) {return false;}}return true;
}// 示例使用
const t = "abcde";
const pos = preprocess(t);
const s = "ace";
console.log(isSubsequenceAdvanced(s, t, pos));
这种方法通过预处理 T 减少了重复计算,提高了处理大量输入时的效率。
相关文章:

31-判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列&#x…...
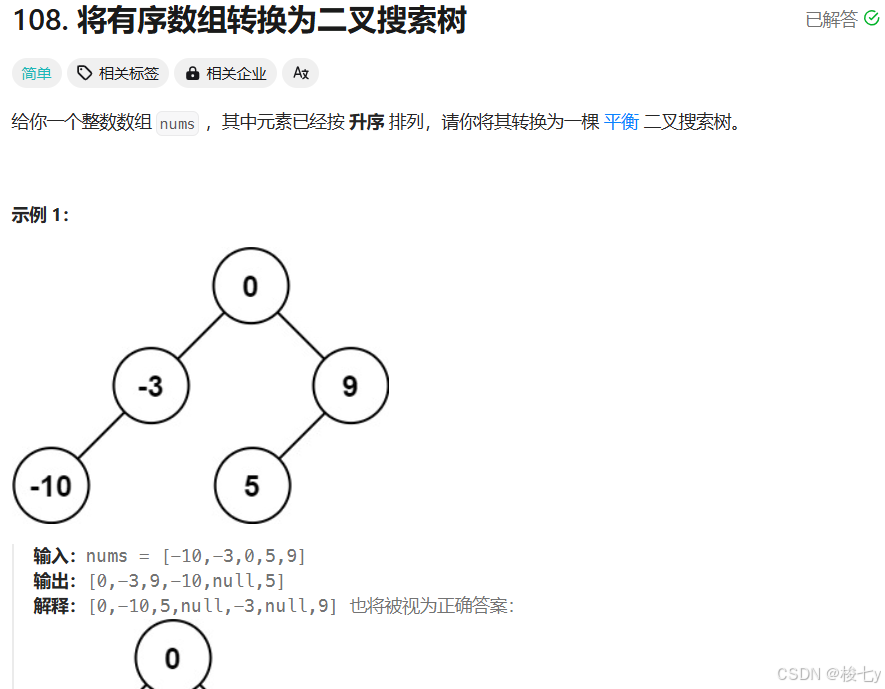
leetcode日记(95)将有序数组转换为二叉搜索树
很简单,感觉自己越来越适应数据结构题目了…… /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : va…...

使用SSH密钥连接本地git 和 github
目录 配置本地SSH,添加到github首先查看本地是否有SSH密钥生成SSH密钥,和邮箱绑定将 SSH 密钥添加到 ssh-agent:显示本地公钥*把下面这一串生成的公钥存到github上* 验证SSH配置是否成功终端跳转到本地仓库把http协议改为SSH(如果…...

C语言基础之【内存管理】
C语言基础之【内存管理】 存储类型作用域普通局部变量静态局部变量普通全局变量静态全局变量全局函数和静态函数 内存布局内存分区存储类型与内存四区内存操作函数memset()memcpy()memmove()memcmp() 堆区内存分配和释放malloc()free() 内存分区代码分析返回栈区地址返回data区…...

C盘清理技巧分享:释放空间,提升电脑性能
目录 1. 引言 2. C盘空间不足的影响 3. C盘清理的必要性 4. C盘清理的具体技巧 4.1 删除临时文件 4.2 清理系统还原点 4.3 卸载不必要的程序 4.4 清理下载文件夹 4.5 移动大文件到其他盘 4.6 清理系统缓存 4.7 使用磁盘清理工具 4.8 清理Windows更新文件 4.9 禁用…...
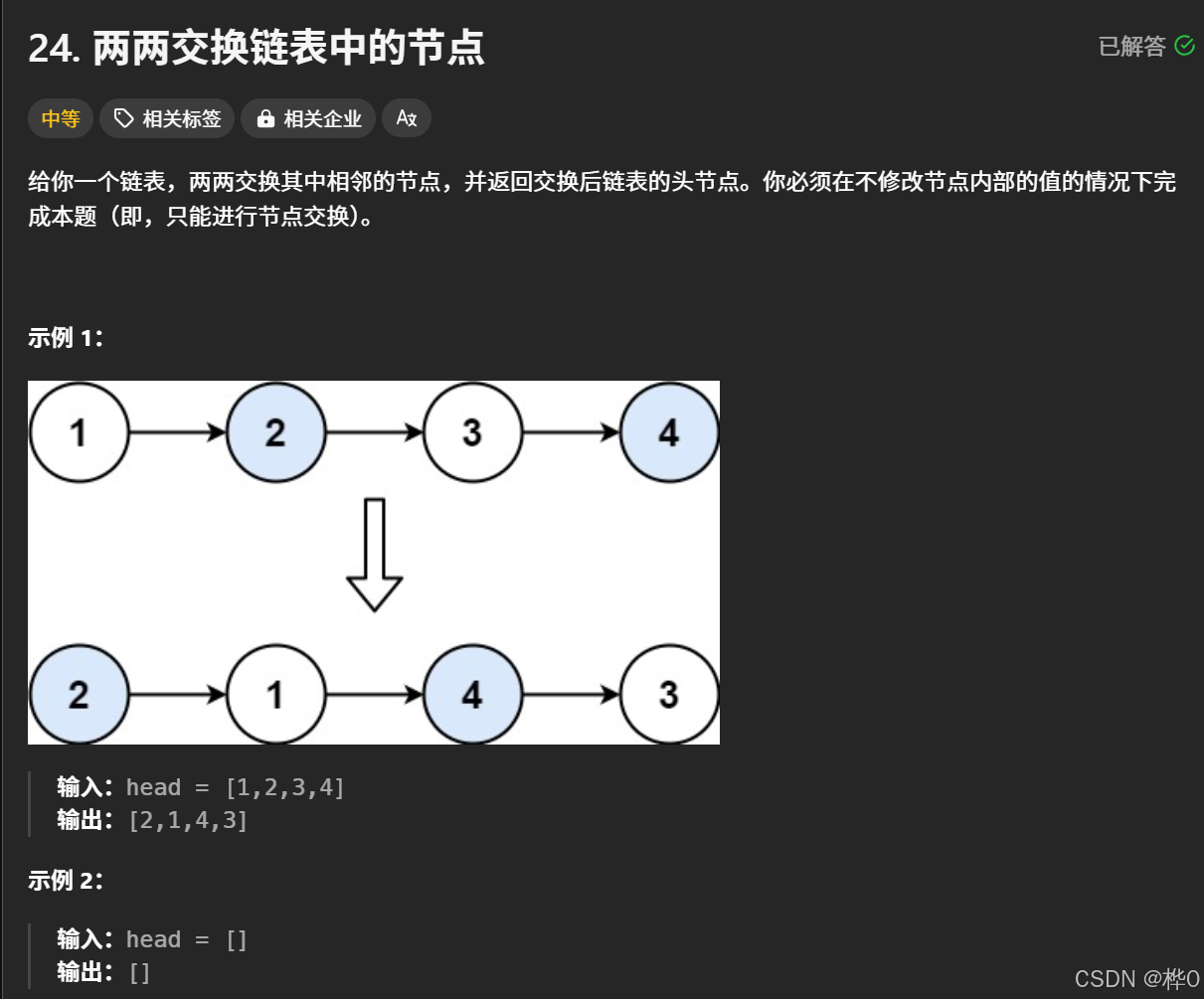
每天一道算法题【蓝桥杯】【两两交换链表中的节点】
思路 本质问题可以分成若干个子问题 即把前两个链表交换,并与后面的链表相连 故实现函数功能调用自身递归即可 #define _CRT_SECURE_NO_WARNINGS 1 struct ListNode {int val;ListNode *next;ListNode() : val(0), next(nullptr) {}ListNode(int x) : val(x), nex…...

mIoU Class与mIoU Category的区别
mIoU(mean Intersection over Union)是语义分割任务中常用的评估指标,用于衡量模型预测的分割结果与真实标签之间的重叠程度。mIoU Class 和 mIoU Category 的区别主要体现在计算方式和应用场景上: 1. mIoU Class 定义ÿ…...

深入解析 C 语言中含数组和指针的构造体与共同体内存计算
在 C 语言中,构造体(struct)和共同体(union)允许我们将多种数据类型组合到一起。除了常见的基本数据类型之外,经常还会在它们中嵌入数组和指针。由于数组的内存是连续分配的,而指针的大小与平台…...
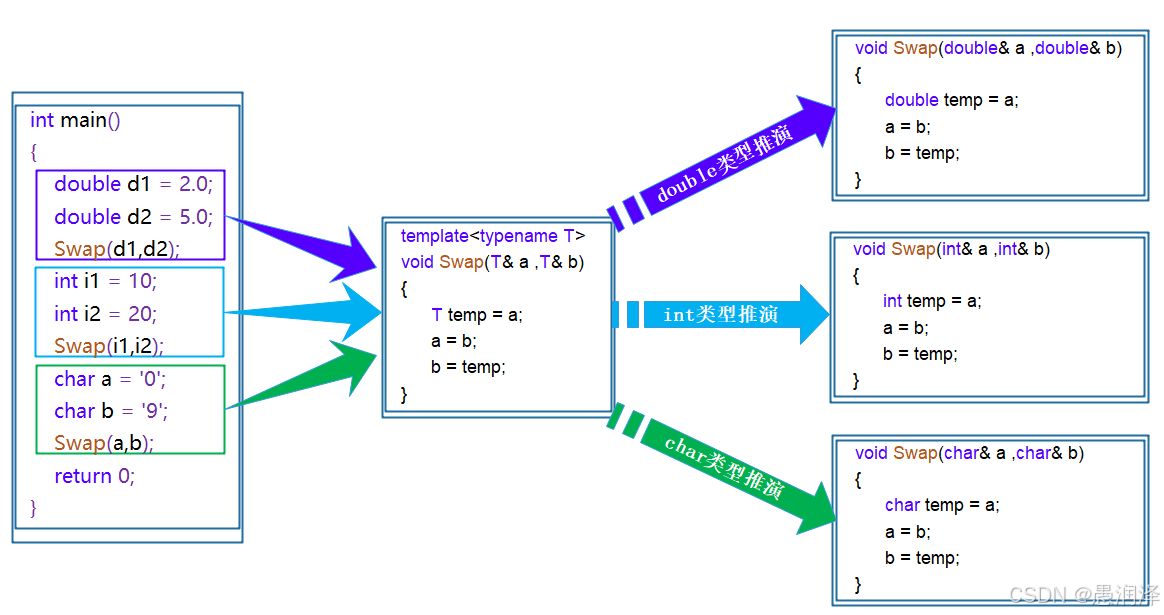
【C++模板】:开启泛型编程之门(函数模版,类模板)
📝前言: 在上一篇文章C内存管理中我们介绍了C的内存管理,重点介绍了与C语言的区别,以及new和delete。这篇文章我们将介绍C的利器——模板。 在C编程世界里,模板是一项强大的特性,它为泛型编程奠定了坚实基础…...

HEC-HMS水文建模全解析:气候变化与极端水文、离散化流域单元精准刻画地表径流、基流与河道演进过程
一、技术革新:数字流域的精密算法革命 在全球气候变化与极端水文事件频发的双重压力下,HEC-HMS模型凭借其半分布式建模架构与多尺度仿真能力,已成为现代流域管理的核心工具。该模型通过离散化流域单元精准刻画地表径流、基流与河…...
具备多种功能的PDF文件处理工具
软件介绍 在日常办公和学习场景中,PDF文件使用极为频繁,而一款功能强大的PDF编辑软件能大幅提升处理效率。 今天要介绍的Adobe Acrobat Pro DC 2024.005.20414,就具备像编辑Word文档一样便捷编辑PDF的能力。 PDF文档在学习和工作中广泛应用…...

【SpringMVC】SpringMVC的启动过程与原理分析:从源码到实战
SpringMVC的启动过程与原理分析:从源码到实战 SpringMVC是Spring框架中用于构建Web应用的核心模块,它基于MVC(Model-View-Controller)设计模式,提供了灵活且强大的Web开发能力。本文将深入分析SpringMVC的启动过程、核…...
转自南京日报:天洑软件创新AI+仿真技术变制造为“智造
以下文章来源:南京日报 进入3月,南京天洑软件有限公司(以下简称天洑软件)董事长张明更加忙碌。“公司强调工业软件在数字经济与先进制造业融合中的关键作用,并已广泛应用在能源、电力和航空等领域。”他说,…...

golang dlv调试工具
golang dlv调试工具 在goland2022.2版本 中调试go程序报错 WARNING: undefined behavior - version of Delve is too old for Go version 1.20.7 (maximum supported version 1.19) 即使你go install了新的dlv也无济于事 分析得出Goland实际使用的是 Goland安装目录下dlv 例…...
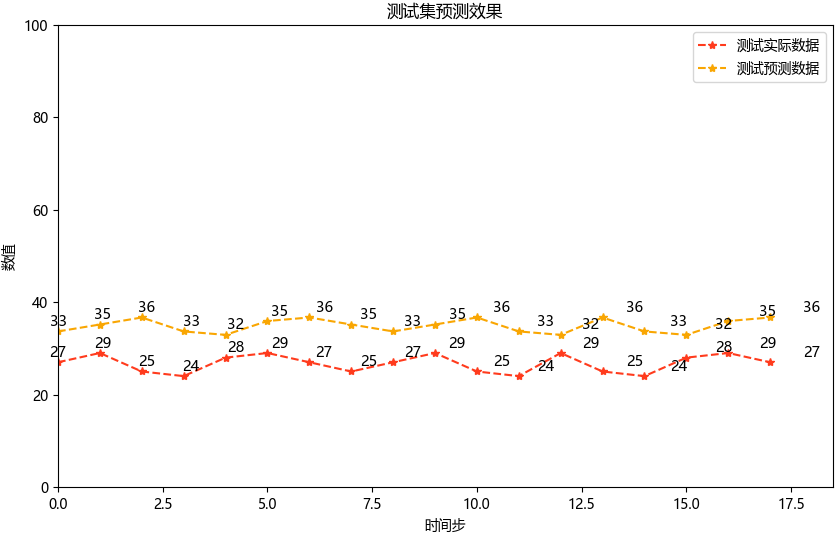
LSTM方法实践——基于LSTM的汽车销量时序建模与预测分析
Hi,大家好,我是半亩花海。本实验基于汽车销量时序数据,使用LSTM网络(长短期记忆网络)构建时间序列预测模型。通过数据预处理、模型训练与评估等完整流程,验证LSTM在短期时序预测中的有效性。 目录 一、实验…...
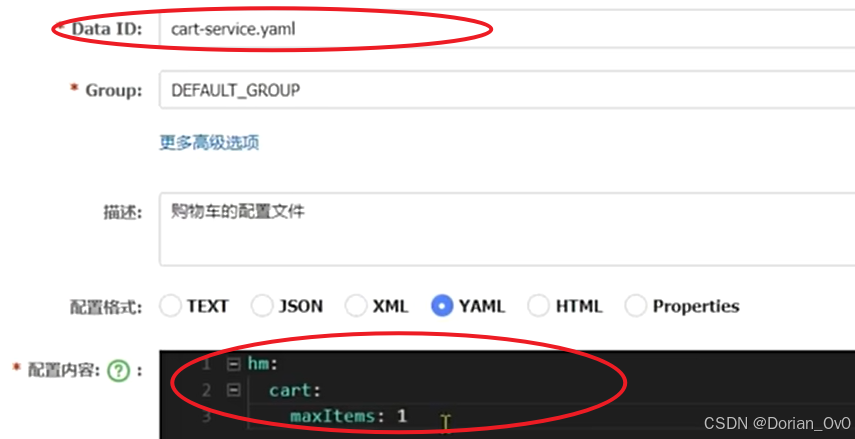
微服务——网关、网关登录校验、OpenFeign传递共享信息、Nacos共享配置以及热更新、动态路由
之前学习了Nacos,用于发现并注册、管理项目里所有的微服务,而OpenFeign简化微服务之间的通信,而为了使得前端可以使用微服务项目里的每一个微服务的接口,就应该将所有微服务的接口管理起来方便前端调用,所以有了网关。…...
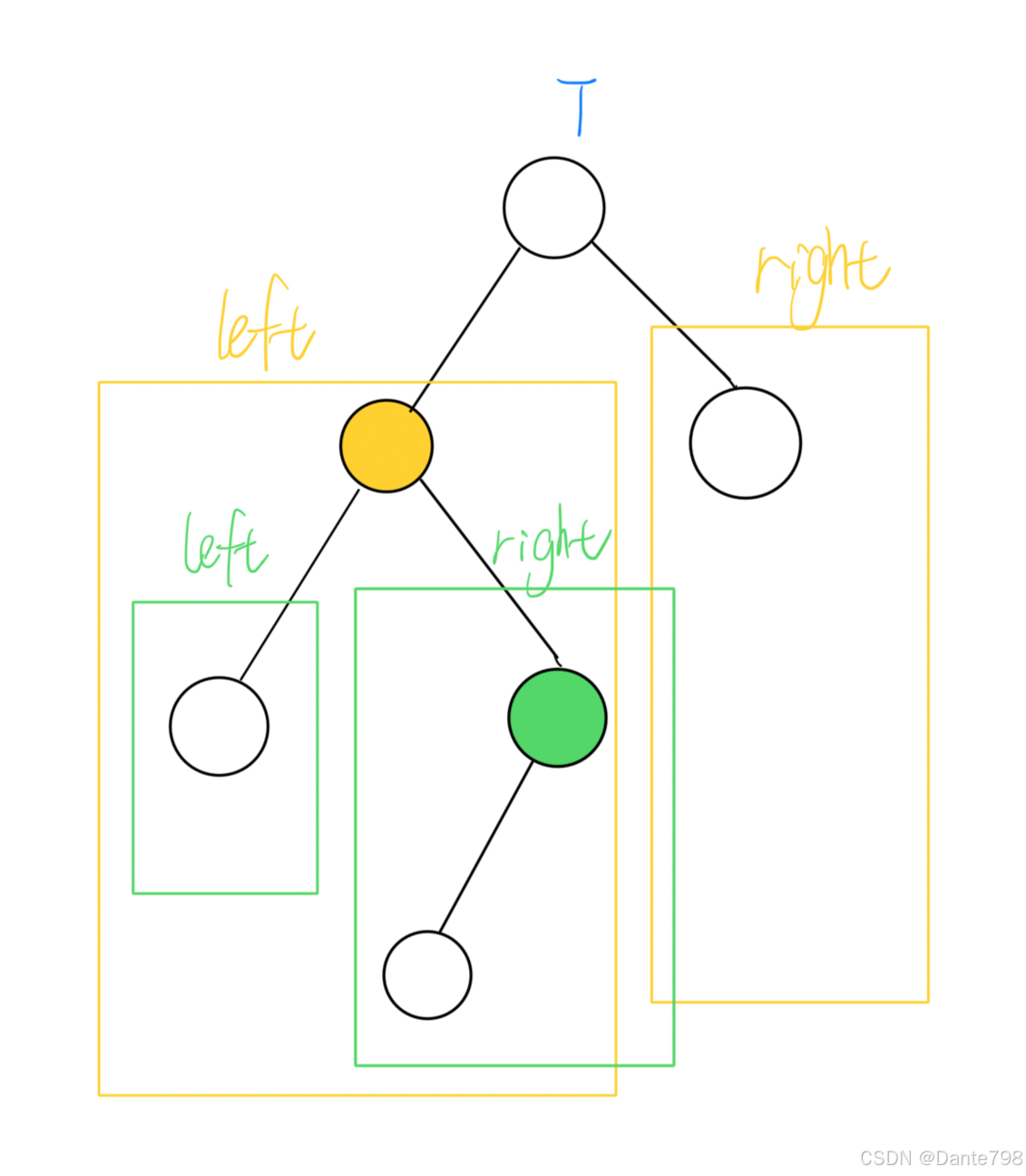
【数据结构】二叉搜索树、平衡搜索树、红黑树
二叉搜索树(Binary Search Tree) 二叉搜索树是一种特殊的二叉树,它用来快速搜索某个值,对于每个节点都应该满足以下条件: 若该节点有左子树,那么左子树中所有节点的值都应该小于该节点的值。若该节点有右…...

Spring Boot 解析 LocalDateTime 失败?Uniapp 传输时间变 1970 的原因与解决方案
目录 前言1. 问题分析2. 时间戳(推荐,可尝试)3. 使用 JsonDeserialize & JsonSerialize(中立)4. 前端传 ISO-8601 格式(不推荐,可尝试)5. 用 String(中立)…...
)
Xilinx ZYNQ FSBL解读:LoadBootImage()
篇首 最近突发奇想,Xilinx 的集成开发环境已经很好了,很多必要的代码都直接生成了,这给开发者带来了巨大便利的同时,也让人错过了很多代码的精彩,可能有很多人用了很多年了,都还无法清楚的理解其中过程。博…...

mysql中in和exists的区别?
大家好,我是锋哥。今天分享关于【mysql中in和exists的区别?】面试题。希望对大家有帮助; mysql中in和exists的区别? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 在 MySQL 中,IN 和 EXISTS 都用于进行子查询,但它…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
