Three.js 无限平面快速教程【Plane】
Three.js 提供了 Plane 概念来表示在 3d 空间中无限延伸的二维表面。 这对于光标交互很有用,因此你可能需要了解如何设置此平面、将其可视化并根据需要进行调整。
推荐:使用 NSDT场景设计器 快速搭建 3D场景。
Three.js 的 Plane 文档很好而且准确,但它肯定假设你是一个“数学人”(我不是),并且如果你从未听说过四元数之类的东西,它不会解释如何让事情正常进行 和平面法线。 我不得不通过老式的艰难方式学习这些东西,所以我为像我这样刚接触 3d 图形的其他开发人员整理了本指南。
首先,最好直观地感受一下什么是平面:你将如何在 3d 空间中表示平面? 我想您可以使用 3 个点定义任何平面,创建一个沿其表面无限延伸的三角形。 三角形的大小无关紧要:只要斜率相同,平面仍然相同。 这是一个 Blender 场景来帮助可视化:
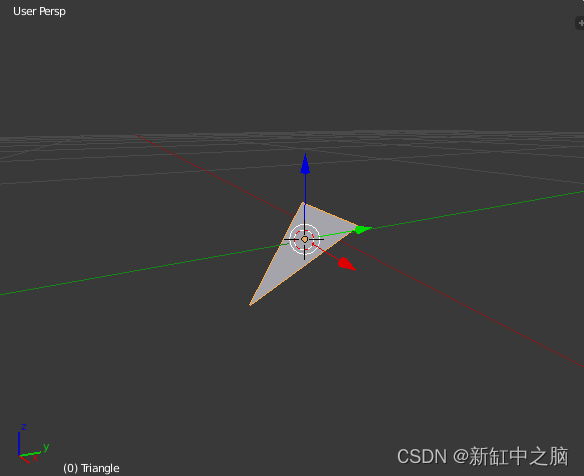
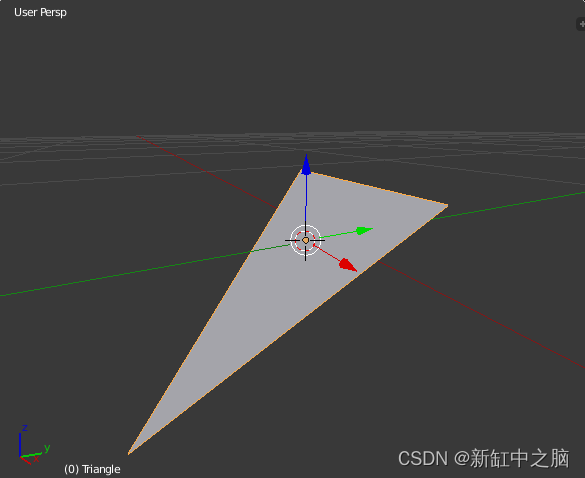
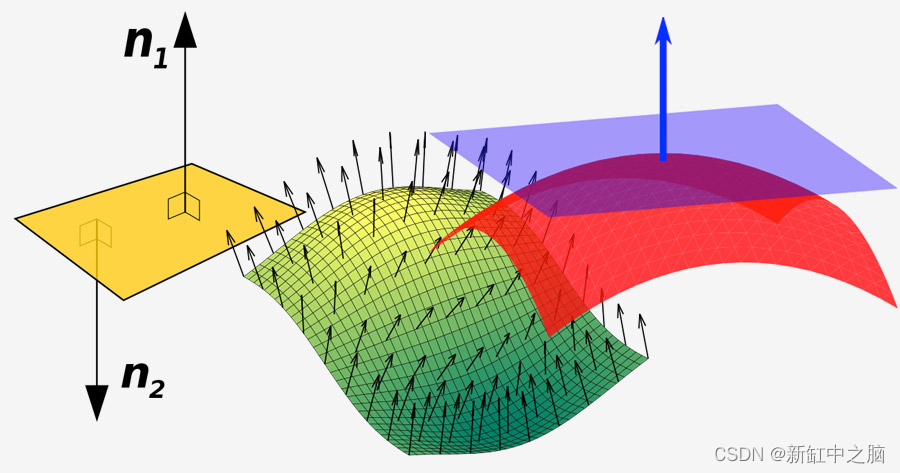
因此,将平面表示为三个点的集合绝对可行,但也许有更好的方法来表示这种结构。 有一个概念叫做表面法线,它是一个垂直于表面的矢量(即指向某个方向的箭头)。 这是维基百科的一张图片,显示了一个带有两个法向量的表面(一个向量由三个参数组成:x、y 和 z):
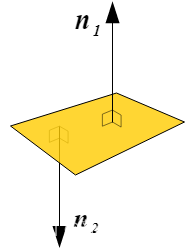
这是曲面法线的图示:
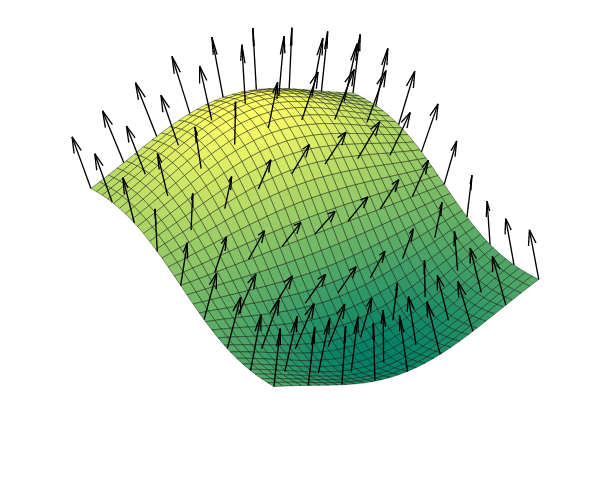
你可以想象每个法线都有一个平面,如下所示:
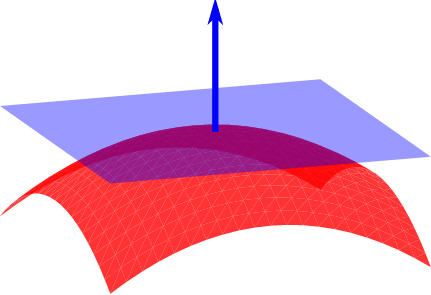
这是 three.js 的 Plane 定义的方式,在其构造函数中清晰可见:
Plane( normal : Vector3, constant : Float )normal - (optional) a unit length Vector3 defining the normal of theplane. Default is (1, 0, 0).constant - (optional) the signed distance from the origin to theplane. Default is 0.
所以要设置一个面朝上的平面,你可以这样做:
var myPlane = new THREE.Plane(new THREE.Vector3(0, 1, 0), 0);
法向量指向上方,因为 y 有一个值,它根本没有被拉向 x 或 z 方向。 事实上,如果将法向量设置为 (0, 2, 0) 或 (0, 200, 0),你会得到完全相同的平面,因为法向量重要的是它的方向,而不是它的大小。 常量值 0 表示该平面的中心恰好位于场景的中心点。
顺便说一下,默认情况下这个平面在你的 three.js 场景中是不可见的。 要查看它,请将 PlaneHelper 连接到它。 这可能会让人感到困惑,但如果你的目标是实际绘制此表面供用户查看,那么你将使用 PlaneGeometry,它继承了 Object3D 的所有基本方法。 我在本文中讨论的 Plane 类只是一个数学平面,但你需要使用这种平面才能使用 Ray.intersectPlane(),这就是你在three.js中将鼠标事件连接到一个平面的方式。
所以,现在你知道如何初始化平面并移动它了。 如果你需要旋转这个东西怎么办? 好吧,你总是可以只更改平面法向量中的参数,对吗? 不过,这实际上是一种非常困难的平面工作方式。 如果你需要将此平面的旋转与场景中已有的可见对象的旋转相匹配,或者只是应用诸如 45 度旋转偏移之类的东西,那么乱用法向量可能会令人沮丧。 我将介绍一些使用一些工具旋转该平面的基本模式。
你将需要学习如何使用四元数。 它们看起来真的很复杂,但你只需要知道它们是一组定义 three.js 对象当前旋转状态的坐标,每个 Object3D 都有一个。 你可以使用 three.js 的 API 将更改应用于四元数并修改它们以执行需要执行的操作。
// There's an object in the scene - myObject - and
// I want to take its rotation and make my plane
// have the same rotation.
var rotation = myObject.quaternion.clone();// The default forward vector for 3D objects is (0, 0, 1),
// so first set the normal to match myObject like that,
// and then make the plane's rotation match myObject as well.
myPlane.normal.set(0, 0, 1).applyQuaternion(rotation);
在将四元数应用于平面之前,还可以根据需要对其进行任何更改。 假设你需要在此旋转上进行 90 度偏移:
var offset = new THREE.Quaternion();offset.setFromAxisAngle(// This rotation offset is along the X axis,// so use a vector where X is 1 here.new THREE.Vector3(1, 0, 0), // Offset by -90 degrees (in radians)-Math.PI / 2);// Modify the rotation
rotation.multiply(offset);// The 'rotation' quaternion is now ready to be applied to the plane
我知道,对于一些简单的旋转来说,这似乎是很多繁琐的事情。 只需将其视为工具包中的另一种模式即可。 其实three.js的Plane API中加入一些简单的旋转机制已经讨论过了。 你不能像 Object3D 一样旋转 Plane 的原因背后的数学原理有点超出我的理解,但听起来好像是因为 Plane 没有“局部坐标系”。
所以这篇文章有点密集。 但我希望它对进入 three.js 这个领域的任何人都有帮助。 这也可以看作是抽象的证明:确实可以让 3D 图形满足你的需求,而无需理解其背后的所有数学原理,并且你会逐渐感受到使用矢量和各种坐标系。
原文链接:Three.js无限平面 — BimAnt
相关文章:

Three.js 无限平面快速教程【Plane】
Three.js 提供了 Plane 概念来表示在 3d 空间中无限延伸的二维表面。 这对于光标交互很有用,因此你可能需要了解如何设置此平面、将其可视化并根据需要进行调整。 推荐:使用 NSDT场景设计器 快速搭建 3D场景。 Three.js 的 Plane 文档很好而且准确&…...
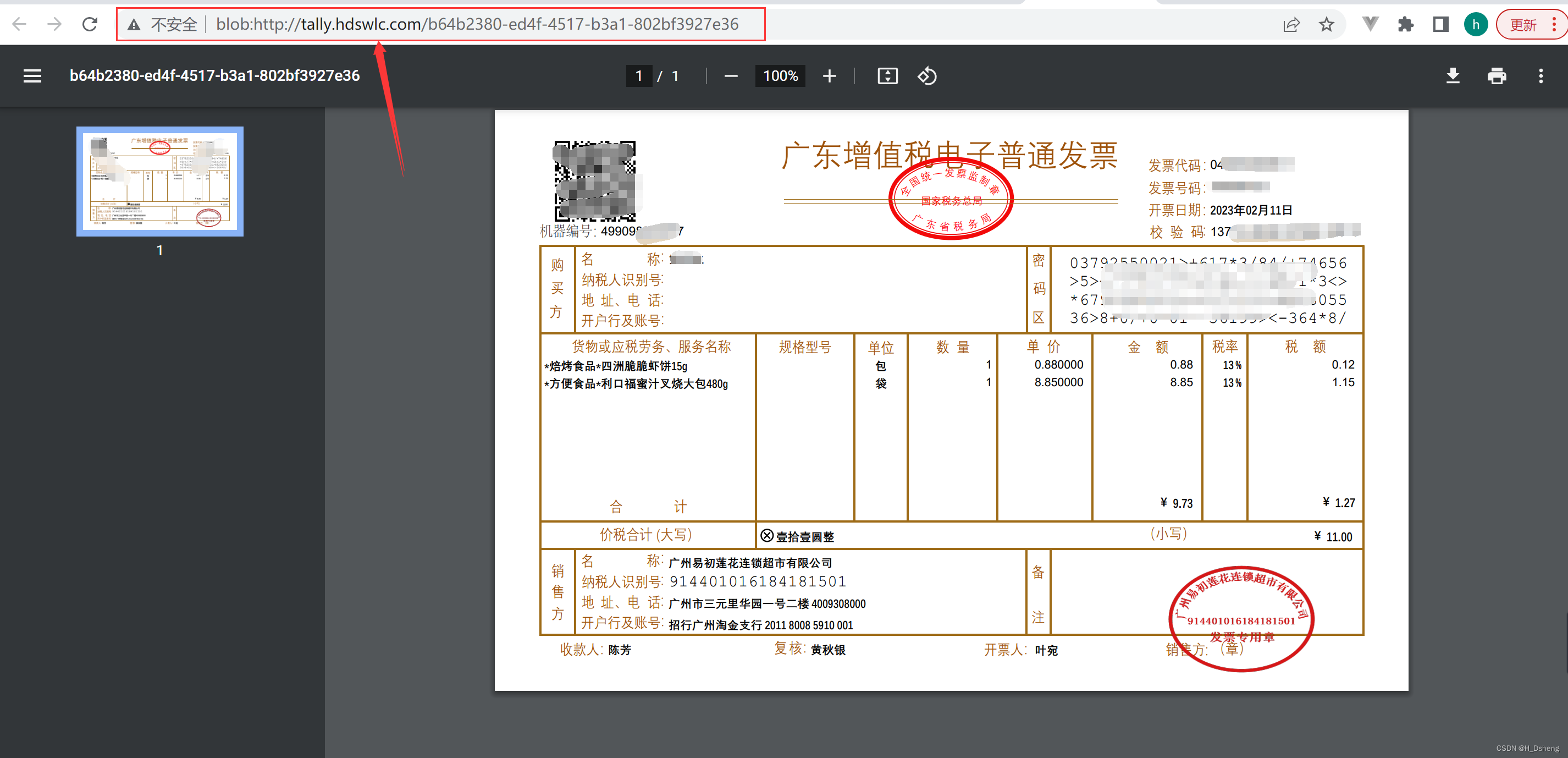
在线预览PDF文件、图片,并且预览地址不显示文件或图片的真实路径。
实现在线预览PDF文件、图片,并且预览地址不显示文件或图片的真实路径。1、vue使用blob流在线预览PDF、图片(包括jpg、png等格式)。1、按钮的方法:2、方法详细:(此方法可以在发起请求时携带token,…...
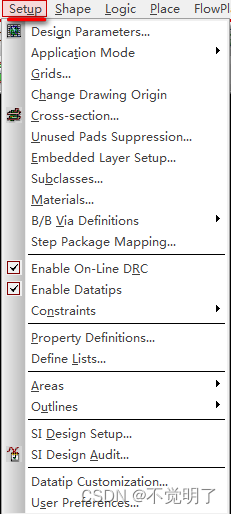
Allegro如何设置导入Subdrawing可自由选择目录操作指导
Allegro如何设置导入Subdrawing可自由选择目录操作指导 用Allgro做PCB设计的时候,导入Subdrawing是非常常用的功能,在导入Subdrawing的时候,通常需要把Subdrawing文件放在需要导入PCB的相同目录下,不能自由选择,如下图 但是Allegro是支持自由选择目录的,只需按照下方的步…...

SpirngMVC执行原理--自学版
DispatcherServlet表示前置控制器,是整个SpringMVC的控制中心,用户发出请求,DispatcherServlet接收请求并拦截请求HandlerMapper为处理器映射。DispatcherServlet调用。HandlerMapping根据请求url查找HandlerHandlerExecution表示具体的Handl…...

获取savemodel的输入输出节点
saved_model_cli show --dir savemodels --all 结果: MetaGraphDef with tag-set: ‘serve’ contains the following SignatureDefs: signature_def[‘translation_signature’]: The given SavedModel SignatureDef contains the following input(s): inputs[‘i…...
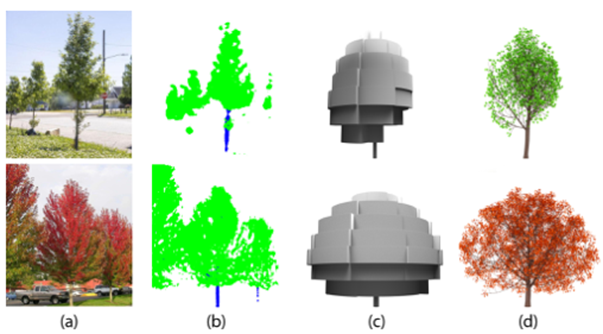
《Learning to Reconstruct Botanical Trees from Single Images》学习从单幅图像重建植物树
读书报告下载https://download.csdn.net/download/weixin_43042683/87448211论文原文https://dl.acm.org/doi/10.1145/3478513.3480525论文视频https://www.bilibili.com/video/BV1cb4y127Vp/?fromseopage&vd_source5212838c127b01db69dcc8b2d27ca5171引言植物存在在室外与…...

vant 4 正式发布,支持暗黑主题,那么是如何实现的呢
2022年10月25日首发于掘金,现在同步到公众号。11. 前言大家好,我是若川。我倾力持续组织了一年多源码共读,感兴趣的可以加我微信 lxchuan12 参与。另外,想学源码,极力推荐关注我写的专栏《学习源码整体架构系列》&…...

MySQL的复制 二
复制是MySQL的一项功能,使服务器能够将更改从一个实例恢复到另一个实例 主服务器(master)将所有数据和结构更改记录到二进制日志中。二进制日志格式是基于语句的、基于行的和混合的。 从属服务器(slave)从主服务器请求…...
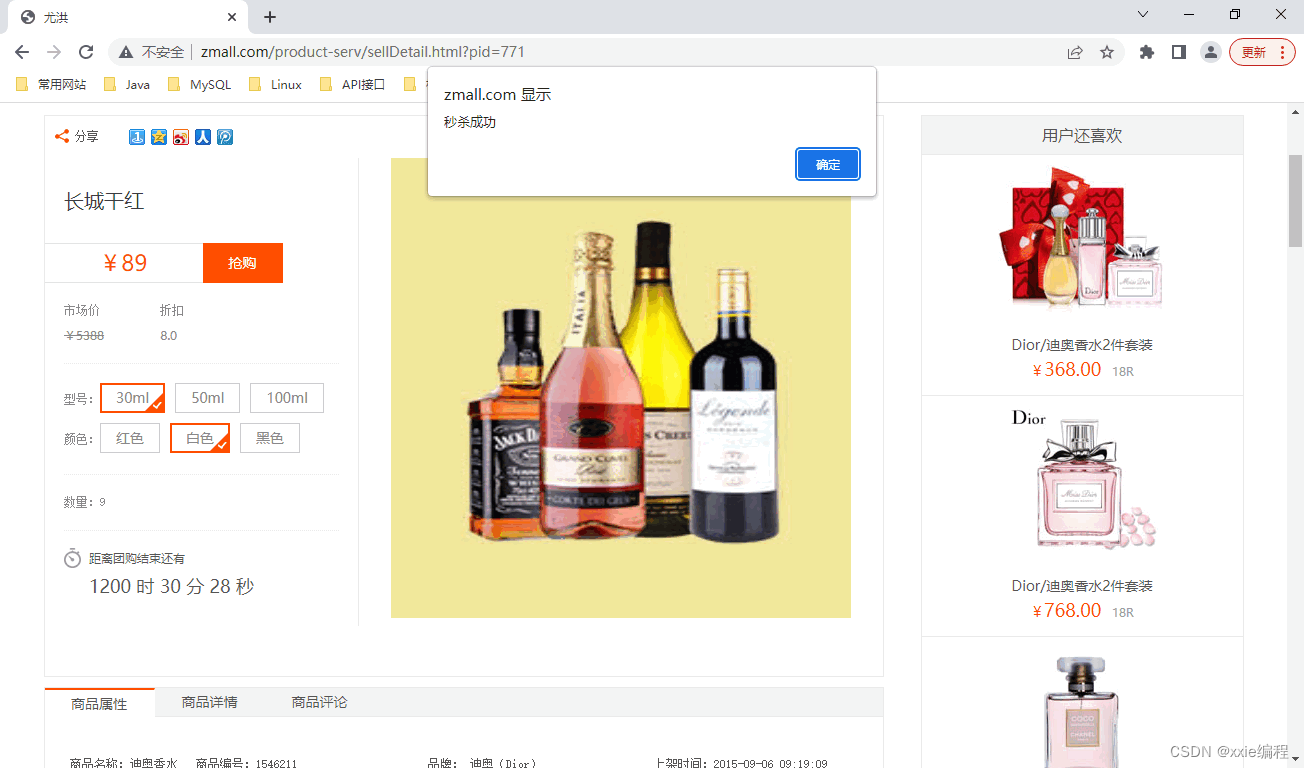
秒杀项目之秒杀商品展示及商品秒杀
目录前言一、登录方式调整二、生成秒杀订单2.1 绑定秒杀商品2.2 查看秒杀商品2.3 订单秒杀2.3.1 移除seata相关(方便测压)2.3.2 生成秒杀订单2.3.3 前端页面秒杀测试注意前言 博主博客用到的资源都会同步分享到资源包中 一、登录方式调整 第1步…...

教育行业需要什么样的数字产品?
数字化转型的浪潮已经席卷了各行各业,不仅出现在互联网、电商、建筑等行业,还应用在了教育行业。数字化的教育ERP软件能够在满足学校需求的基础上,帮助学校完善各类工作流程,提高工作效率。 对于一个拥有多个校区,上万…...
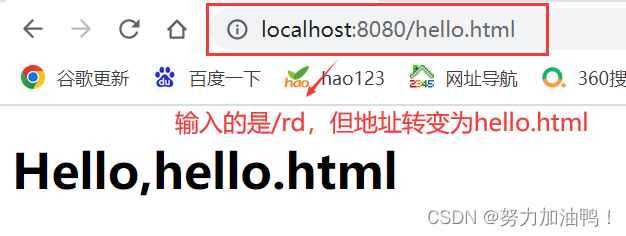
Spring MVC
一、Spring MVC介绍 a. Spring MVC是一个Web框架 b. Spring MVC是基于Servlet API构成的 MVC 是 Model View Controller 的缩写。 MVC 是⼀种思想,⽽ Spring MVC 是对 MVC 思想的具体实现。 学习Spring MVC目标: a.连接功能:将用户ÿ…...

类与对象(上)
类与对象(上) 1.面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题的步骤,通过函数调用逐步解决问题。 C是基于面向对象的,关注的是对象,将一件事情拆分成不同的对象,靠对象之间…...

正确安装 torch_geometric库
step1: 查看pytorchcuda 版本 torch-scatter torch-sparse torch-cluster torch-spline-conv 这些关联包要与torch版本匹配。 import torch print(torch.__version__) print(torch.cuda.is_available()) torch.version.cuda或者 pip list查看版本 step2ÿ…...
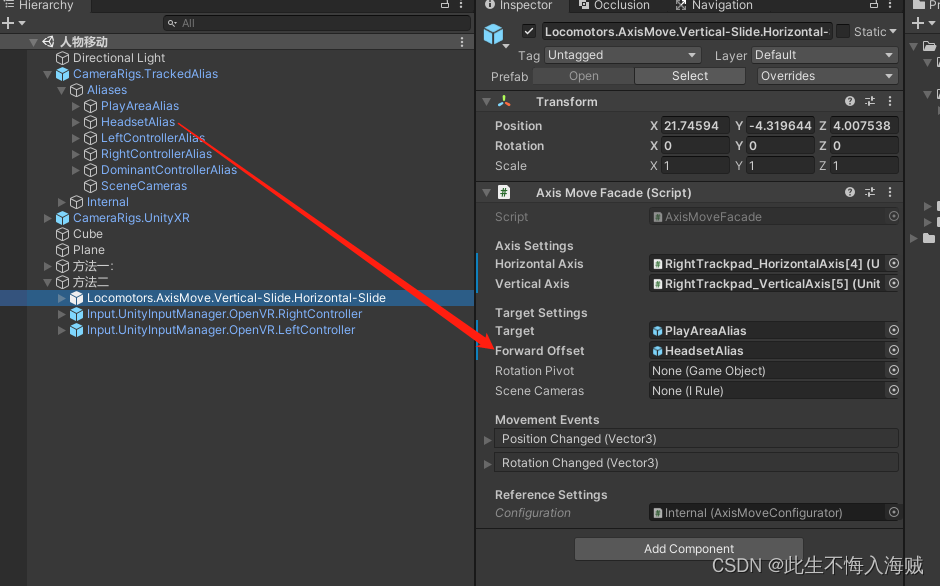
【Unity VR开发】结合VRTK4.0:自身移动(滑动)
语录: 依山傍水房树间,行也安然,住也安然; 一条耕牛半顷田,收也凭天,荒也凭天; 雨过天晴驾小船,鱼在一边,酒在一边; 夜晚妻子话灯前,今也谈谈…...
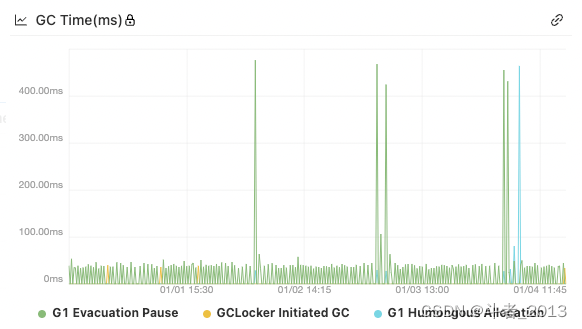
G1垃圾回收器详解
文章目录前言一、思考问题二、官方文档三、基本介绍四、G1的内存模型五、G1的标记过程六、G1的垃圾回收1、G1过程梳理2、Young GC3、Mixed GC4、Full GC七、参数介绍八、典型问题1、疏散失败(Evacuation Failure)2、大对象分配(Humongous All…...

tws耳机哪个牌子音质好?tws耳机音质排行榜
随着蓝牙耳机市场的不断发展,使用蓝牙耳机的人也逐渐增多,近年来更是超越有线耳机成为最火爆的数码产品之一。那么,tws耳机哪个牌子音质好?下面,我来给大家推荐几款音质好的tws耳机,可以当个参考。 一、南…...

TIA博途中DB数据块清零的具体方法示例
TIA博途中DB数据块清零的具体方法示例 TIA中数据块如何实现清零? 在TIA指令集内有多个移动指令可对DB块内数据进行清零处理。对于S7-1500 CPU或ET200SP CPU来说,可使用BLKMOV、FILL以及SCL的POKE_BLK指令。但是这些指令对DB块清零时,要求DB块必需为非优化DB。 对于优化的DB…...
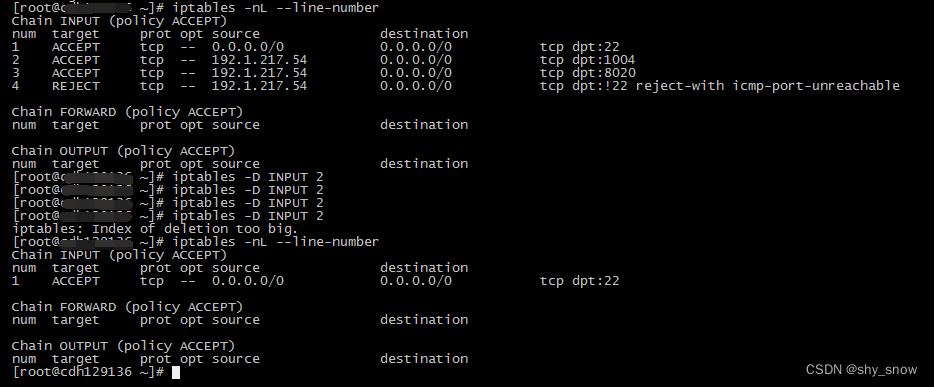
iptables防火墙屏蔽指定ip的端口
因为需要测试客户端程序与hadoop服务器之间正常通信需要开通的端口, 所以在hadoop各服务器上使用iptables防火墙屏蔽了测试客户端程序的ip和所有端口。然后,根据报错信息提示的端口号来逐步放开直到能正常通信下载文件。 在服务器端屏蔽指定ip访问所有端口 #查看…...
 对象)
JavaScript Math(算数) 对象
JavaScript Math(算数) 对象 Math 是一个内置对象,它拥有一些数学常数属性和数学函数方法。Math 不是一个函数对象。 Math 用于 Number 类型。它不支持 BigInt。 描述 与其他全局对象不同的是,Math 不是一个构造器。Math 的所…...

超详细的JAVA高级进阶基础知识04
目录 4. 面向对象高级 - 常用的API 4.1 Arrays 工具类 4.1.1 Arrays 类介绍 4.2 冒泡排序 4.3 选择排序 4.4 二分查找 4.5 正则表达式 4.5.1 String 类中与正则有关的常见方法 4.5.2 练习 4.5.3 今日学习目标 4. 面向对象高级 - 常用的API 4.1 Arrays 工具类 4.1.1…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
