[JavaScript 刷题] 特殊数组的特征值, leetcode 1608
[JavaScript 刷题] 特殊数组的特征值, leetcode 1608
这道题在一个列表上看到的,刚开始用暴力解想过了就过了,不过后面看了一下关键字,发现解法……非常有趣。
时间复杂度可以从 O(n2)O(n^2)O(n2) 降为 O(nlog(n))O(n log(n))O(nlog(n)),再降为 O(n)O(n)O(n),顺便记一下学习过程,毕竟很少看到简单题这么复杂的。
题目
You are given an array
numsof non-negative integers.numsis considered special if there exists a numberxsuch that there are exactlyxnumbers innumsthat are greater than or equal tox.Notice that
xdoes not have to be an element innums.Return
xif the array is special, otherwise, return-1. It can be proven that ifnumsis special, the value forxis unique.
解题思路
暴力解
题意问的是是否存在特殊数字 x,使得数组中出现大于等于 x 的数字正好等同鱼 x 本身。假设数组中所有的数字都比 x 大,那么最多存在 nums.length 个数字,反之则是 0。
这道题给的上限是 1 <= nums.length <= 100,也就是说 x 的上限为 100,暴力解的时间复杂度就是 n2n^2n2,也就是 10000,所以不会超时(甚至还没一些题目的 input 多)。
暴力解的做法就是遍历两次数组,每次便利的时候记录大于等于当前值 i 出现的次数,如果计算出来正好等于 i,则可以直接返回当前 i,解法如下:
function specialArray(nums: number[]): number {for (let i = 1; i <= nums.length; i++) {let counter = 0;for (let j = 0; j < nums.length; j++) {console.log(nums[j], counter);if (nums[j] >= i) counter++;if (counter > i) break;}if (counter === i) return i;}return -1;
}
排序
另一种思路是排序去做,排序完了之后只需要从大到小找比当前的 i 大的数字出现的次数即可。
以 [3,6,7,7,0] 为例,排序后的结果为 [7, 7, 6, 3, 0]。
当 x = 1,7>17 > 17>1 所以继续执行。
当 x = 2,7>27 > 27>2 所以继续执行。
当 x = 3,6>26 > 26>2 所以继续执行。
当 x = 4,3<43 < 43<4,已经不满足存在于 x 个数字大于等于 x 本身这一条件,因此可以直接返回 −1-1−1。
解法如下:
function specialArray(nums: number[]): number {nums.sort((a, b) => b - a);let x: number = -1;for (let i = 1; i <= nums.length; i++) {if (nums[i - 1] >= i) {x = i;continue;}if (nums[i - 1] >= x) return -1;}return x;
}
这样的解法时间复杂度为 $ O(nlog(n))$,会比暴力解更加的有效。
二分搜索
二分算法的过程以及原理和排序就有点相似,已知结果只可能存在于 1<=x<=1001 <= x <= 1001<=x<=100,因此对这个区间进行二分搜索,找到出现 >=x>= x>=x 的数字正好出现 xxx 次的这个值。
function specialArray(nums: number[]): number {let left = 1,right = nums.length;while (left <= right) {const mid = Math.floor((left + right) / 2);const count = nums.reduce((accum, curr) => (mid <= curr ? accum + 1 : accum),0);if (count === mid) return mid;if (count > mid) left = mid + 1;else right = mid - 1;}// need to check when left is also a posible solutionconst count = nums.reduce((accum, curr) => (left <= curr ? accum + 1 : accum),0);return count === left ? left : -1;
}
虽然也是 $ O(nlog(n)),不过二分算法少走了一个遍历,因此速度相比较而言会快一些(,不过二分算法少走了一个遍历,因此速度相比较而言会快一些(,不过二分算法少走了一个遍历,因此速度相比较而言会快一些(left <= nums.length$ 是肯定的),不过大 O 都一样。
桶排序
桶排序利用的是所有的数字都可能会被归类到 1−1001 - 1001−100 的这个容器中,将所有的数字全都归类到对应的桶里进行倒叙的频率检查,最后找到符合条件的特殊数字即可。
function specialArray(nums: number[]): number {const length = nums.length;const buckets = new Array(length + 1).fill(0);for (const num of nums) {buckets[Math.min(num, length)] += 1;}let count = 0;for (let i = length; i > 0; i--) {// since it's frequence, so we can check count directly after adding the frequencycount += buckets[i];if (count === i) return count;}return -1;
}
这里走了两个遍历,所以时间复杂度是 O(n)O(n)O(n),应该来说是没办法找到更优的解法了。
相关文章:

[JavaScript 刷题] 特殊数组的特征值, leetcode 1608
[JavaScript 刷题] 特殊数组的特征值, leetcode 1608 这道题在一个列表上看到的,刚开始用暴力解想过了就过了,不过后面看了一下关键字,发现解法……非常有趣。 时间复杂度可以从 O(n2)O(n^2)O(n2) 降为 O(nlog(n))O(n log(n))O(nlog(n))&am…...

各种素材网站大全【全部倾倒,福利倒计时-JS,HTML,游戏素材,UI,图片素材等
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 收录于专栏:解忧杂货铺 ⭐各种素材网站大全⭐ 文章目录⭐各种素材网站大全⭐🎶大家必逛的四大天王…...

影片自由,丝滑流畅,Docker容器基于WebDav协议通过Alist挂载(百度网盘/阿里云盘)Python3.10接入
使用过NAS(Network Attached Storage)的朋友都知道,它可以通过局域网将本地硬盘转换为局域网内的“网盘”,简单理解就是搭建自己的“私有云”,但是硬件和网络成本都太高了,有点可望而不可及的意思。Alist开源库则可以满足我们&…...
| 运气好,这就是原题)
【新】华为OD机试 - 数组的中心位置(Python)| 运气好,这就是原题
数组的中心位置 题目 给你一个整数数组nums,请计算数组的中心位置。 数组中心位置是数组的一个下标,其左侧所有元素相乘的积等于右侧所有元素相乘的积。 数组第一个元素的左侧积为1,最后一个元素的右侧积为1。 如果数组有多个中心位置,应该返回最靠近左边的那一个。 如果数…...
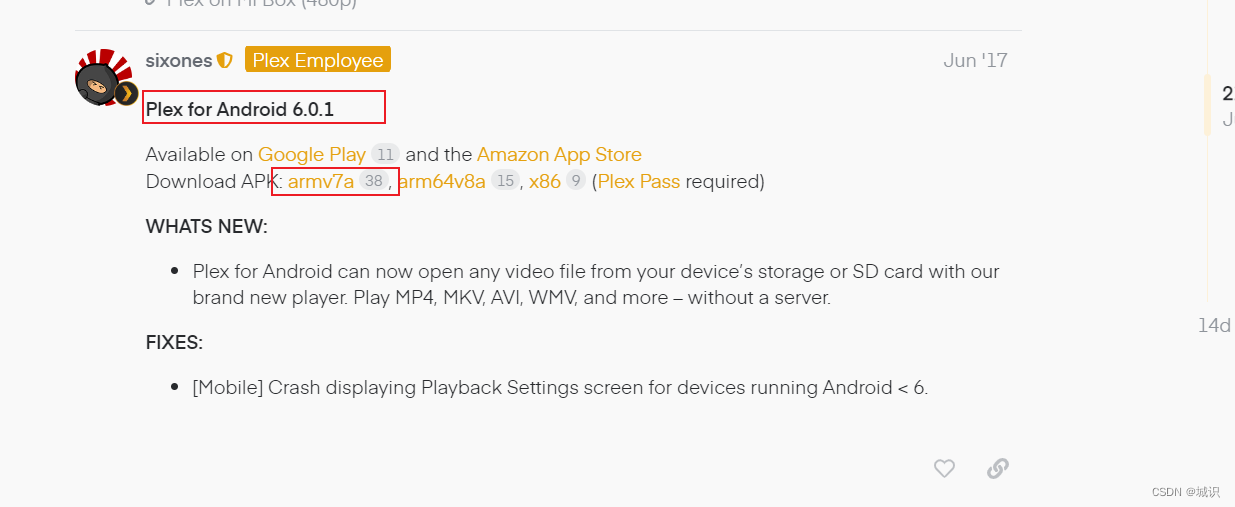
小米电视安装 Plex 打造家庭影院
背景 最近突然想重温教父,本来想着直接投屏就可以,后来看了别人搭建的基于 NAS 的家庭影院很动心,也想依葫芦画瓢做一个,跟对象申请经费的时候被拒了,理由是有这钱还不如开个会员直接看。 我寻思不同电影在不同的平台…...

Elasticsearch:Combined fields 查询
有时一个匹配项可以覆盖多个文本字段。 在这种情况下,你可以使用 combined_fields 查询来搜索多个文本字段,就好像它们的值实际上已被索引到一个组合字段中一样。 除此之外,combined_fields 的主要好处是强大且易于理解的评分算法。这种做法也…...

uart 子系统
串口硬件储备知识: uart 在Linux 应用层的体现及使用 uart 就是串口,它也是属于字符设备中的一种,众所周知 字符设备都会在/dev/ 目录下创建节点,串口所创建的节点名都是以tty* 为开头,例如下面这些节点:…...
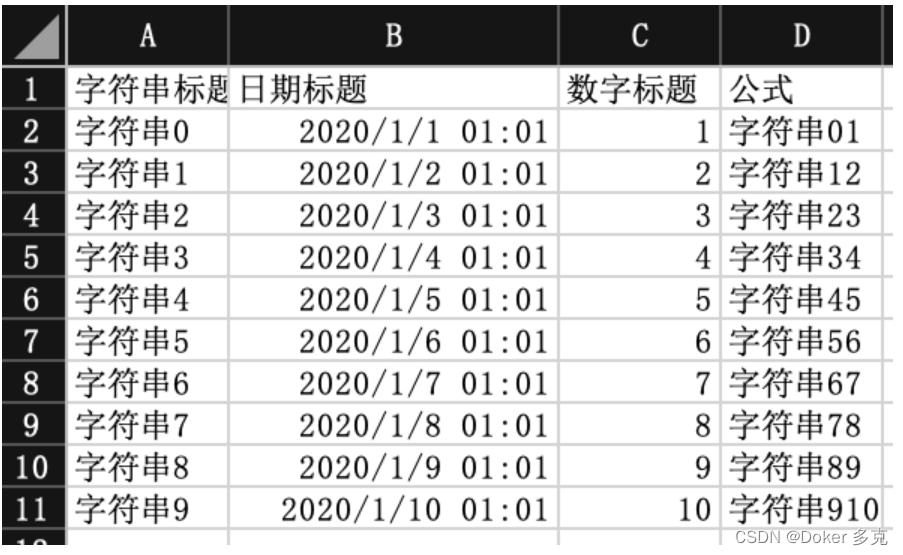
SpringBoot 整合EasyExcel详解
一、概述 Java解析、生成Excel比较有名的框架有Apache poi、jxl。但他们都存在一个严重的问题就是非常的耗内存,poi有一套SAX模式的API可以一定程度的解决一些内存溢出的问题,但POI还是有一些缺陷,比如07版Excel解压缩以及解压后存储都是在内…...

VScode+cuda编程:常见环境问题
VScodecuda:常见环境配置问题1、VScode终端问题(PS)2、编译问题(CUDA版本过低)3、nvcc编译问题(arch架构)1、VScode终端问题(PS) 问题描述: 在VScode下打开终端执行nvcc指令,发现执行不了,但是在外部终端powershell和cmd都可以。…...
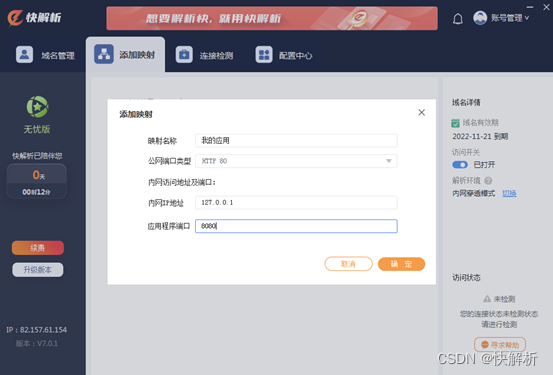
简单实用的内网穿透实现教程
内网穿透,字面理解就是网络地址穿透,是一种比较常用的将内网地址转换成公网地址的方式。通过内网穿透,可以将本地内网局域网提供给外网公网上访问,在外网也能连接访问内网主机和应用,当用户有日常远程和异地外网访问的…...

makefile案例学习
makefile案例学习 很多时候, 我们在git clone完一个project之后,就会让我们使用make命令进行项目的构建。这个make命令的背后就是按照了Makefile文件定义的格式去完成项目构建。 因此Makefile的作用就是帮助程序员进行项目的构建,它按照项目…...
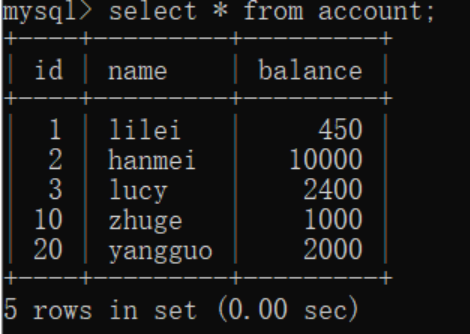
MySQL性能优化六 事物隔离级别与锁机制
概述 我们的数据库一般都会并发执行多个事务,多个事务可能会并发的对相同的一批数据进行增删改查操作,可能就会导致我们说的脏写、脏读、不可重复读、幻读这些问题。 这些问题的本质都是数据库的多事务并发问题,为了解决多事务并发问题&#…...
四数之和-力扣18-java排序+双指针
一、题目描述给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):…...

操作系统开发:BIOS/MBR基础与调试
这里在实验之前需要下载 Bochs-win32-2.6.11 作者使用的是Linux版本的,在Linux写代码不太舒服,所以最好在Windows上做实验,下载好虚拟机以后还需要下载Nasm汇编器,以及GCC编译器,为了能够使用DD命令实现磁盘拷贝&#…...
)
华为OD机试真题JAVA实现【数组合并】真题+解题思路+代码(20222023)
🔥系列专栏 华为OD机试(JAVA)真题目录汇总华为OD机试(Python)真题目录汇总华为OD机试(C++)真题目录汇总华为OD机试(JavaScript)真题目录汇总文章目录 🔥系列专栏题目输入输出示例一输入输出示例二输入输出解题思路核心知识点...

说说Real DOM和Virtual DOM的区别?优缺点?
说说Real DOM和Virtual DOM的区别?优缺点?Real DOM(真实的DOM)真实dom的优缺点?Virtual DOM(虚拟的DOM)虚拟dom的优缺点?两者的区别Real DOM(真实的DOM) 在页面渲染出的每个节点都是一个真实的DOM结构 <div class"root&…...
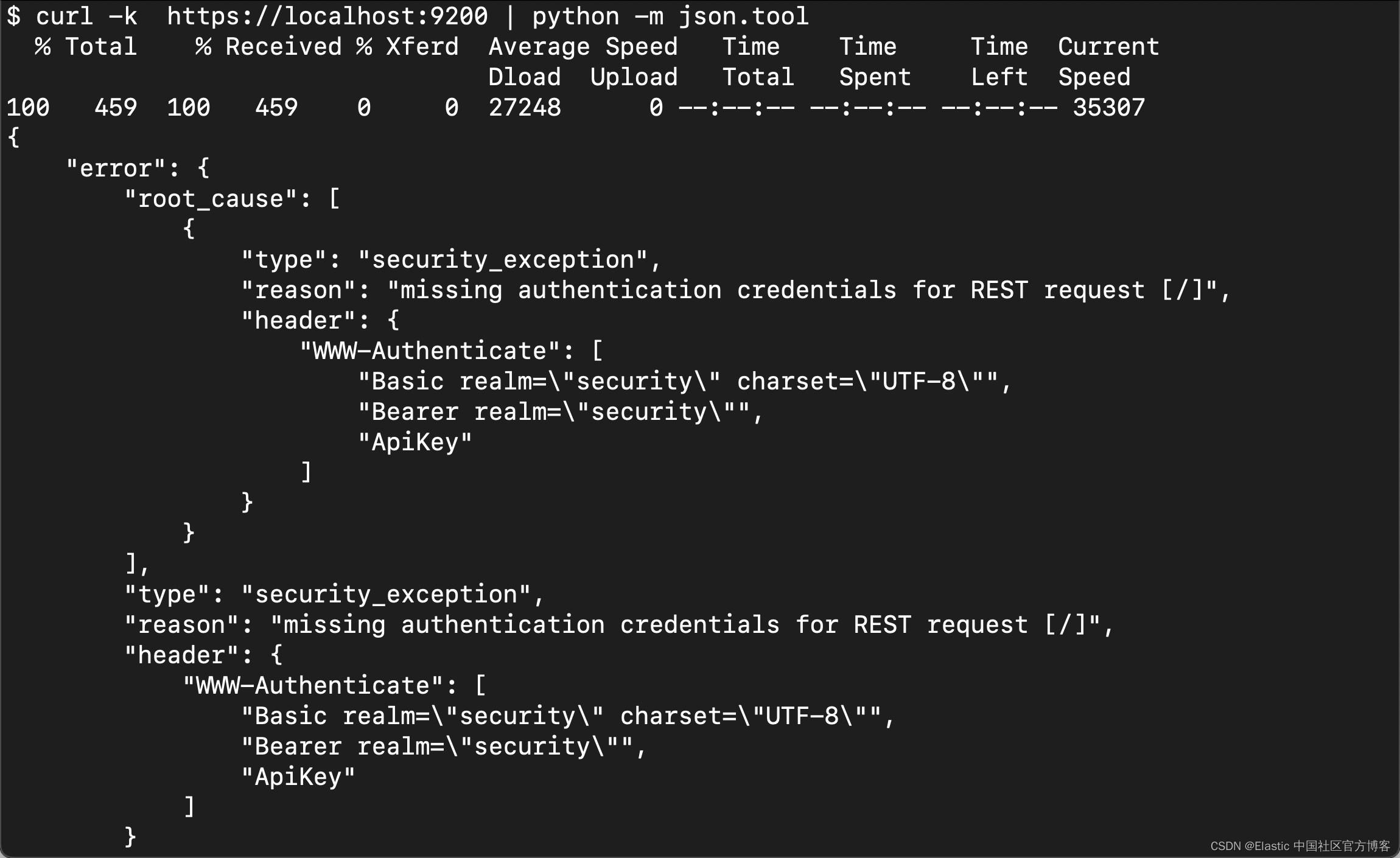
使用脚本以可读的 JSON 格式显示 curl 命令输出
在我们经常调试微服务或者使用 Elasticsearch API 时,经常会使用curl 来进行调试。但是有时我们的输出不尽如意。显示的不是一 pretty 格式进行输出的。我们有时还必须借助于其他的一些网站工具,比如 Best JSON Formatter and JSON Validator: Online JS…...

计算机网络9:HTTP和HTTPS的区别
1.HTTP和HTTPS的区别 (1)安全性 HTTP是超文本传输协议,信息传输存在安全问题HTTPS是安全套接字超文本传输协议,在TCP和HTTP之间加入了SSL/TLS安全协议,进行加密传输 (2)连接步骤HTTP建立相对简…...

Spring+SpringMVC+SpringBoot+MyBatis面试题
什么是Spring框架?使用Spring框架的好处是什么?Spring是一款开源的轻量级Java开发框架,可以提高开发人员的开发效率以及系统的可维护性。Spring框架是很多模块的集合,使用这些模块可以很方便地协助我们进行开发,比如说…...

ContextCapture Master 倾斜摄影测量实景三维建模技术
ContextCapture实景建模大师是一套无需人工干预,通过影像自动生成高分辨率的三维模型的软件解决方案。它集合了全球最先进数字影像处理、计算机虚拟现实以及计算机几何图形算法,在易用性、数据兼容性、运算性能、友好的人机交互及自由的硬件配置兼容性等…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
