动态规划专题——背包问题
🧑💻 文章作者:Iareges
🔗 博客主页:https://blog.csdn.net/raelum
⚠️ 转载请注明出处
目录
- 前言
- 一、01背包
- 1.1 使用滚动数组优化
- 二、完全背包
- 2.1 使用滚动数组优化
- 三、多重背包
- 3.1 使用二进制优化
- 四、分组背包
- 总结
前言
本文主要介绍常见的四种背包问题,思维导图如下:
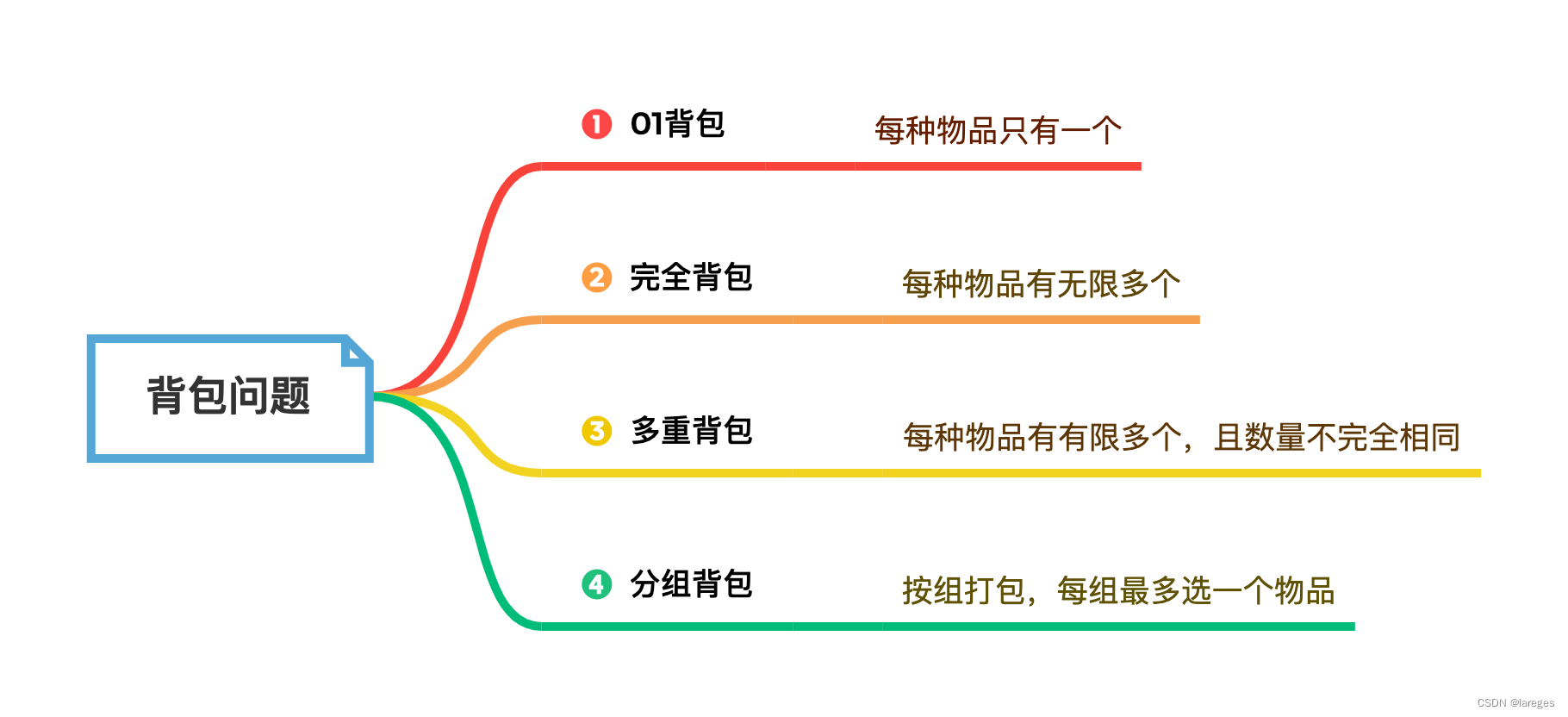
一、01背包
💡 现有 NNN 件物品和一个最多能承重 MMM 的背包,第 iii 件物品的重量是 wiw_iwi,价值是 viv_ivi。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。
因为每件物品只有选与不选两种状态,所以该问题又称01背包问题。
设 dp[i][j]dp[i][j]dp[i][j] 的含义是:在背包承重为 jjj 的前提下,从前 iii 个物品中选能够得到的最大价值。不难发现 dp[N][M]dp[N][M]dp[N][M] 就是本题的答案。
如何计算 dp[i][j]dp[i][j]dp[i][j] 呢?我们可以将它划分为以下两部分:
- 选第 iii 个物品:由于第 iii 个物品一定会被选择,那么相当于从前 i−1i-1i−1 个物品中选且总重量不超过 j−w[i]j-w[i]j−w[i],对应 dp[i−1][j−w[i]]+v[i]dp[i-1][j-w[i]]+v[i]dp[i−1][j−w[i]]+v[i]。
- 不选第 iii 个物品:意味着从前 i−1i-1i−1 个物品中选且总重量不超过 jjj,对应 dp[i−1][j]dp[i-1][j]dp[i−1][j]。
结合以上两点可得递推公式:
dp[i][j]=max(dp[i−1][j],dp[i−1][j−w[i]]+v[i])dp[i][j] = \max(dp[i-1][j],\;dp[i-1][j-w[i]]+v[i]) dp[i][j]=max(dp[i−1][j],dp[i−1][j−w[i]]+v[i])
由于下标不能是负数,所以上述递推公式要求 j≥w[i]j\geq w[i]j≥w[i]。当 j<w[i]j<w[i]j<w[i] 时,意味着第 iii 个物品无法装进背包,此时 dp[i][j]=dp[i−1][j]dp[i][j]=dp[i-1][j]dp[i][j]=dp[i−1][j]。综合以上可得出:
dp[i][j]={dp[i−1][j],j<w[i]max(dp[i−1][j],dp[i−1][j−w[i]]+v[i]),j≥w[i]dp[i][j]= \begin{cases} dp[i-1][j],&j<w[i] \\ \max(dp[i-1][j],\;dp[i-1][j-w[i]]+v[i]),&j\geq w[i] \end{cases} dp[i][j]={dp[i−1][j],max(dp[i−1][j],dp[i−1][j−w[i]]+v[i]),j<w[i]j≥w[i]
dpdpdp 数组应当如何初始化呢?当背包承重为 000 时,显然装不下任何物品,所以 dp[i][0]=0(1≤i≤N)dp[i][0]=0\;(1\leq i\leq N)dp[i][0]=0(1≤i≤N)。若一个物品也不选(即从前 000 个物品中选),此时最大价值也是 000,所以 dp[0][j]=0(0≤j≤M)dp[0][j]=0\;(0\leq j\leq M)dp[0][j]=0(0≤j≤M)。由此可知,dpdpdp 数组应当全0初始化,即声明为全局变量。
题目链接:AcWing 2. 01背包问题
#include <bits/stdc++.h>using namespace std;const int N = 1010;int w[N], v[N];
int dp[N][N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (j < w[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);}}cout << dp[n][m] << "\n";return 0;
}
时间复杂度为 O(nm)O(nm)O(nm)。
1.1 使用滚动数组优化
之前我们用到的 dpdpdp 数组是二维数组,它可以进一步优化成一维数组。
观察递推公式不难发现,dpdpdp 数组中第 iii 行的元素仅由第 i−1i-1i−1 行的元素得来,即第 000 行元素的更新值放到第 111 行,第 111 行元素的更新值放到第 222 行,以此类推。与其把一行的更新值放到新的一行,不如直接就地更新,因此我们的 dpdpdp 数组只需要一行来存储,即一维数组。
去掉 dpdpdp 数组的第一维后,递推公式变成:
dp[j]={dp[j],j<w[i]max(dp[j],dp[j−w[i]]+v[i]),j≥w[i]dp[j]= \begin{cases} dp[j],&j<w[i] \\ \max(dp[j],\;dp[j-w[i]]+v[i]),&j\geq w[i] \end{cases} dp[j]={dp[j],max(dp[j],dp[j−w[i]]+v[i]),j<w[i]j≥w[i]
即
dp[j]=max(dp[j],dp[j−w[i]]+v[i]),j≥w[i]dp[j]= \max(dp[j],\;dp[j-w[i]]+v[i]),\quad j\geq w[i] dp[j]=max(dp[j],dp[j−w[i]]+v[i]),j≥w[i]
原先 jjj 是从 111 遍历至 mmm 的,现在只需从 w[i]w[i]w[i] 遍历至 mmm。但,这个遍历顺序真的对吗?
请看下图:

红色箭头表示,在二维数组中,dp[i][j]dp[i][j]dp[i][j] 由 dp[i−1][j−w[i]]dp[i-1][j-w[i]]dp[i−1][j−w[i]] 和 dp[i−1][j]dp[i-1][j]dp[i−1][j] 得来,dp[i][j+w[i]]dp[i][j+w[i]]dp[i][j+w[i]] 由 dp[i−1][j]dp[i-1][j]dp[i−1][j] 和 dp[i−1][j+w[i]]dp[i-1][j+w[i]]dp[i−1][j+w[i]] 得来。用一维数组的话来讲就是,第 iii 行的 dp[j]dp[j]dp[j] 由第 i−1i-1i−1 行的 dp[j−w[i]]dp[j-w[i]]dp[j−w[i]] 和 dp[j]dp[j]dp[j] 得来,第 iii 行的 dp[j+w[i]]dp[j+w[i]]dp[j+w[i]] 由第 i−1i-1i−1 行的 dp[j]dp[j]dp[j] 和 dp[j+w[i]]dp[j+w[i]]dp[j+w[i]] 得来。
如果 jjj 从小到大遍历,那么会先更新 dp[j]dp[j]dp[j] 再更新 dp[j+w[i]]dp[j+w[i]]dp[j+w[i]],这就导致在更新 dp[j+w[i]]dp[j+w[i]]dp[j+w[i]] 时使用的是第 iii 行的 dp[j]dp[j]dp[j] 而非第 i−1i-1i−1 行的 dp[j]dp[j]dp[j],即当 jjj 从小到大遍历时,二维数组的递推式变成了:
dp[i][j]={dp[i−1][j],j<w[i]max(dp[i−1][j],dp[i][j−w[i]]+v[i]),j≥w[i]dp[i][j]= \begin{cases} dp[i-1][j],&j<w[i] \\ \max(dp[i-1][j],\;dp[i][j-w[i]]+v[i]),&j\geq w[i] \end{cases} dp[i][j]={dp[i−1][j],max(dp[i−1][j],dp[i][j−w[i]]+v[i]),j<w[i]j≥w[i]
⚠️ 请牢记该式,后续讲解完全背包时会提到它。
这显然是错误的。事实上,让 jjj 从大到小遍历就不会出现这个问题。
#include <bits/stdc++.h>using namespace std;const int N = 1010;int w[N], v[N];
int dp[N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];for (int i = 1; i <= n; i++)for (int j = m; j >= w[i]; j--)dp[j] = max(dp[j], dp[j - w[i]] + v[i]);cout << dp[m] << "\n";return 0;
}
当然,www 数组和 vvv 数组也是不必要的,我们可以边输入边处理,因此可以得到01背包问题的最终版代码:
#include <bits/stdc++.h>using namespace std;const int N = 1010;int dp[N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) {int w, v;cin >> w >> v;for (int j = m; j >= w; j--)dp[j] = max(dp[j], dp[j - w] + v);}cout << dp[m] << "\n";return 0;
}
到此为止,可以总结出,当 dpdpdp 数组是二维数组时,jjj 既可以从小到大遍历也可以从大到小遍历,但当 dpdpdp 数组是一维数组时,jjj 只能从大到小遍历。
二、完全背包
💡 现有 NNN 种物品和一个最多能承重 MMM 的背包,每种物品都有无限个,第 iii 种物品的重量是 wiw_iwi,价值是 viv_ivi。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。
设 dp[i][j]dp[i][j]dp[i][j] 的含义是:在背包承重为 jjj 的前提下,从前 iii 种物品中选能够得到的最大价值。
如何计算 dp[i][j]dp[i][j]dp[i][j] 呢?我们可以将它划分为以下若干部分:
- 选 000 个第 iii 种物品:相当于不选第 iii 种物品,对应 dp[i−1][j]dp[i-1][j]dp[i−1][j]。
- 选 111 个第 iii 种物品:对应 dp[i−1][j−w[i]]+v[i]dp[i-1][j-w[i]]+v[i]dp[i−1][j−w[i]]+v[i]。
- 选 222 个第 iii 种物品:对应 dp[i−1][j−2⋅w[i]]+2⋅v[i]dp[i-1][j-2\cdot w[i]]+2\cdot v[i]dp[i−1][j−2⋅w[i]]+2⋅v[i]。
- ⋯\cdots⋯
上述过程并不会无限进行下去,因为背包承重是有限的。设第 iii 种物品最多能选 ttt 个,于是可知 t=⌊jw[i]⌋t=\lfloor \frac{j}{w[i]}\rfloort=⌊w[i]j⌋,从而得到递推式:
dp[i][j]=max0≤k≤tdp[i−1][j−k⋅w[i]]+k⋅v[i]dp[i][j]=\max_{0\leq k\leq t} dp[i-1][j-k\cdot w[i]]+k\cdot v[i] dp[i][j]=0≤k≤tmaxdp[i−1][j−k⋅w[i]]+k⋅v[i]
题目链接:AcWing 3. 完全背包问题
#include <bits/stdc++.h>using namespace std;const int N = 1010;int w[N], v[N];
int dp[N][N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++) {int t = j / w[i];for (int k = 0; k <= t; k++)dp[i][j] = max(dp[i][j], dp[i - 1][j - k * w[i]] + k * v[i]);}cout << dp[n][m] << "\n";return 0;
}
若将 ttt 的值改为 min(1,j/w[i])\min(1,\,j/w[i])min(1,j/w[i]),则完全背包将退化为01背包。
上述代码的时间复杂度为 O(m2∑iwi−1)≈O(m2n)O(m^2\sum_iw_i^{-1})\approx O(m^2n)O(m2∑iwi−1)≈O(m2n),TLE是必然的。
2.1 使用滚动数组优化
考虑 dp[i][j]dp[i][j]dp[i][j],此时第 iii 种物品最多能选 t1=⌊jw[i]⌋t_1=\lfloor \frac{j}{w[i]} \rfloort1=⌊w[i]j⌋ 个,将递推式展开:
dp[i][j]=max(dp[i−1][j],dp[i−1][j−w[i]]+v[i],dp[i−1][j−2⋅w[i]]+2⋅v[i],⋮dp[i−1][j−t1⋅w[i]]+t1⋅v[i])\begin{aligned} dp[i][j] = \max(dp[i-1][j],\; &dp[i-1][j-w[i]]+v[i], \\ &dp[i-1][j-2\cdot w[i]]+2\cdot v[i], \\ &\vdots \\ &dp[i-1][j-t_1\cdot w[i]]+t_1\cdot v[i]) \end{aligned} dp[i][j]=max(dp[i−1][j],dp[i−1][j−w[i]]+v[i],dp[i−1][j−2⋅w[i]]+2⋅v[i],⋮dp[i−1][j−t1⋅w[i]]+t1⋅v[i])
下面考虑 dp[i][j−w[i]]dp[i][j-w[i]]dp[i][j−w[i]],此时第 iii 种物品最多能选 t2=⌊j−w[i]w[i]⌋=⌊jw[i]−1⌋=t1−1t_2=\lfloor \frac{j-w[i]}{w[i]} \rfloor=\lfloor \frac{j}{w[i]}-1\rfloor=t_1-1t2=⌊w[i]j−w[i]⌋=⌊w[i]j−1⌋=t1−1 个,相应的递推式为
dp[i][j−w[i]]=max(dp[i−1][j−w[i]],dp[i−1][j−w[i]−w[i]]+v[i],dp[i−1][j−w[i]−2⋅w[i]]+2⋅v[i],⋮dp[i−1][j−w[i]−t2⋅w[i]]+t2⋅v[i])\begin{aligned} dp[i][j-w[i]] = \max(dp[i-1][j-w[i]],\; &dp[i-1][j-w[i]-w[i]]+v[i], \\ &dp[i-1][j-w[i]-2\cdot w[i]]+2\cdot v[i], \\ &\vdots \\ &dp[i-1][j-w[i]-t_2\cdot w[i]]+t_2\cdot v[i]) \end{aligned} dp[i][j−w[i]]=max(dp[i−1][j−w[i]],dp[i−1][j−w[i]−w[i]]+v[i],dp[i−1][j−w[i]−2⋅w[i]]+2⋅v[i],⋮dp[i−1][j−w[i]−t2⋅w[i]]+t2⋅v[i])
又注意到 t1=t2+1t_1=t_2+1t1=t2+1,上式可化简为
dp[i][j−w[i]]=max(dp[i−1][j−w[i]],dp[i−1][j−2⋅w[i]]+v[i],dp[i−1][j−3⋅w[i]]+2⋅v[i],⋮dp[i−1][j−t1⋅w[i]]+(t1−1)⋅v[i])\begin{aligned} dp[i][j-w[i]] = \max(dp[i-1][j-w[i]],\; &dp[i-1][j-2\cdot w[i]]+v[i], \\ &dp[i-1][j-3\cdot w[i]]+2\cdot v[i], \\ &\vdots \\ &dp[i-1][j-t_1\cdot w[i]]+(t_1-1)\cdot v[i]) \end{aligned} dp[i][j−w[i]]=max(dp[i−1][j−w[i]],dp[i−1][j−2⋅w[i]]+v[i],dp[i−1][j−3⋅w[i]]+2⋅v[i],⋮dp[i−1][j−t1⋅w[i]]+(t1−1)⋅v[i])
将该式与 dp[i][j]dp[i][j]dp[i][j] 的递推式比较不难发现
dp[i][j]=max(dp[i−1][j],dp[i][j−w[i]]+v[i])dp[i][j]=\max(dp[i-1][j],\;dp[i][j-w[i]]+v[i]) dp[i][j]=max(dp[i−1][j],dp[i][j−w[i]]+v[i])
根据1.1节中的结论,该式对应的是 jjj 从小到大遍历,于是我们只需把01背包问题的代码中的 jjj 改为从小到大遍历即可。
#include <bits/stdc++.h>using namespace std;const int N = 1010;int dp[N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) {int w, v;cin >> w >> v;for (int j = w; j <= m; j++) // 只需修改这一行dp[j] = max(dp[j], dp[j - w] + v);}cout << dp[m] << "\n";return 0;
}
优化后的时间复杂度为 O(nm)O(nm)O(nm)。
三、多重背包
💡 现有 NNN 种物品和一个最多能承重 MMM 的背包,第 iii 种物品的数量是 sis_isi,重量是 wiw_iwi,价值是 viv_ivi。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。
回顾完全背包问题的暴力解法,在背包承重为 jjj 的前提下,第 iii 种物品最多能放 t=j/w[i]t=j/w[i]t=j/w[i] 个(这里是整除)。而在01背包问题中,第 iii 种物品只有一个,所以应当取 t=min(1,j/w[i])t=\min(1,\,j/w[i])t=min(1,j/w[i])。由此可见,对于多重背包问题,只需取 t=min(s[i],j/w[i])t=\min(s[i],\,j/w[i])t=min(s[i],j/w[i])。
对完全背包问题的暴力解法做一点简单修改即可求解多重背包问题。
题目链接:AcWing 4. 多重背包问题
#include <bits/stdc++.h>using namespace std;const int N = 110;int dp[N][N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) {int w, v, s;cin >> w >> v >> s;for (int j = 1; j <= m; j++) {int t = min(s, j / w); // 只有这里需要修改for (int k = 0; k <= t; k++)dp[i][j] = max(dp[i][j], dp[i - 1][j - k * w] + k * v);}}cout << dp[n][m] << "\n";return 0;
}
时间复杂度为 O(m∑isi)O(m\sum_i s_i)O(m∑isi),但还可以进一步优化。
3.1 使用二进制优化
从时间复杂度的表达式可以看出,O(m)O(m)O(m) 的部分已经无法再优化了,我们只能从 O(∑isi)O(\sum_i s_i)O(∑isi) 入手。
先来看一个例子。水果店里有 404040 个苹果,小明计划购买 n(1≤n≤40)n\,(1\leq n\leq 40)n(1≤n≤40) 个苹果,试问如何让小明尽可能快速地完成购买?一个显而易见的暴力做法是,让小明一个个拿(单位是个),但效率过于低下。事实上,店员可事先准备好 666 个箱子,每个箱子中的苹果数量分别为 [1,2,4,8,16,9][1,2,4,8,16,9][1,2,4,8,16,9],再让小明按箱子拿(单位是箱子),无论小明计划购买多少个,他最多只需要拿 666 次,而在暴力做法中,小明最多需要拿 404040 次。
下面用数学语言来描述上面的例子。对于任意的正整数 sss,我们都可以找到 ⌊log2s⌋+1≜k\lfloor \log_2 s\rfloor+1\triangleq k⌊log2s⌋+1≜k 个正整数 a1,⋯,aka_1,\cdots,a_ka1,⋯,ak,使得 ∀n∈[0,s]\forall\, n\in[0,s]∀n∈[0,s],都有
n=vTa,a=(a1,⋯,ak)T,ai={2i−1,1≤i≤k−1r(∈[1,2k−1]),i=kn=v^\mathrm{T}a,\quad a=(a_1,\cdots,a_k)^\mathrm{T},\quad a_i= \begin{cases} 2^{i-1},&1\leq i\leq k -1\\ r\,(\in [1,\,2^{k-1}]),&i=k\\ \end{cases} n=vTa,a=(a1,⋯,ak)T,ai={2i−1,r(∈[1,2k−1]),1≤i≤k−1i=k
其中 v=(v1,⋯,vk)Tv=(v_1,\cdots,v_k)^\mathrm{T}v=(v1,⋯,vk)T,且其分量非 000 即 111。
感兴趣的读者可自行证明,这里不再赘述。回到本题,先不考虑背包的承重,我们在暴力求解多重背包的时候,对于每种物品 iii,都要从 000 逐个枚举至 s[i]s[i]s[i],效率无疑是低下的。现在,对于每种物品 iii,我们将这 s[i]s[i]s[i] 个物品分散至 ⌊log2s[i]⌋+1\lfloor \log_2 s[i]\rfloor+1⌊log2s[i]⌋+1 个「箱子」中,于是多重背包便化成了01背包。
题目链接:AcWing 5. 多重背包问题 II
多重背包问题中的一个「箱子」相当于01背包问题中的一件「物品」,因此我们需要估计出多重背包问题中到底有多少个箱子。显然箱子总数为
N=∑i=1n(⌊log2s[i]⌋+1)≤∑i=1n⌊log22000⌋+n=11n≤11000N=\sum_{i=1}^n(\lfloor \log_2 s[i]\rfloor+1)\leq \sum_{i=1}^n \lfloor \log_2 2000\rfloor+n=11n\leq 11000 N=i=1∑n(⌊log2s[i]⌋+1)≤i=1∑n⌊log22000⌋+n=11n≤11000
#include <bits/stdc++.h>using namespace std;const int N = 11010, M = 2010;int w[N], v[N];
int dp[M];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;int cnt = 0;while (n--) {int a, b, s; // a是重量, b是价值, c是数量cin >> a >> b >> s;for (int k = 1; k <= s; k *= 2) {cnt++;w[cnt] = a * k, v[cnt] = b * k;s -= k;}if (s > 0) {cnt++;w[cnt] = a * s, v[cnt] = b * s;}}n = cnt;for (int i = 1; i <= n; i++)for (int j = m; j >= w[i]; j--)dp[j] = max(dp[j], dp[j - w[i]] + v[i]);cout << dp[m] << "\n";return 0;
}
优化后的时间复杂度为 O(m∑ilogsi)O(m\sum_i \log s_i)O(m∑ilogsi)。
四、分组背包
💡 现有 NNN 组物品和一个最多能承重 MMM 的背包,每组物品有若干个,同一组内的物品最多只能选一个。每件物品的重量是 wijw_{ij}wij,价值是 vijv_{ij}vij,其中 iii 是组号,jjj 是组内编号。在背包能承受的范围内,试问将哪些物品装入背包后可使总价值最大,求这个最大价值。
设 dp[i][j]dp[i][j]dp[i][j] 的含义是:在背包承重为 jjj 的前提下,从前 iii 组物品中选能够得到的最大价值。
如何计算 dp[i][j]dp[i][j]dp[i][j] 呢?我们可以将它划分为以下若干部分:
- 不选第 iii 组的物品:对应 dp[i−1][j]dp[i-1][j]dp[i−1][j]。
- 选第 iii 组的第 111 个物品:对应 dp[i−1][j−w[i][1]]+v[i][1]dp[i-1][j-w[i][1]]+v[i][1]dp[i−1][j−w[i][1]]+v[i][1]。
- 选第 iii 组的第 222 个物品:对应 dp[i−1][j−w[i][2]]+v[i][2]dp[i-1][j-w[i][2]]+v[i][2]dp[i−1][j−w[i][2]]+v[i][2]。
- ⋯\cdots⋯
- 选第 iii 组的第 s[i]s[i]s[i] 个物品:对应 dp[i−1][j−w[i][s[i]]]+v[i][s[i]]dp[i-1][j-w[i][s[i]]]+v[i][s[i]]dp[i−1][j−w[i][s[i]]]+v[i][s[i]]。
直接将 dpdpdp 数组优化到一维可得递推式:
dp[j]=max(dp[j],max1≤k≤s[i]dp[j−w[i][k]]+v[i][k])dp[j]=\max(dp[j],\;\max_{1\leq k\le s[i]} dp[j-w[i][k]]+v[i][k]) dp[j]=max(dp[j],1≤k≤s[i]maxdp[j−w[i][k]]+v[i][k])
题目链接:AcWing 9. 分组背包问题
#include <bits/stdc++.h>using namespace std;const int N = 110;int w[N][N], v[N][N], s[N];
int dp[N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> s[i];for (int j = 1; j <= s[i]; j++)cin >> w[i][j] >> v[i][j];}for (int i = 1; i <= n; i++)for (int j = m; j >= 1; j--)for (int k = 1; k <= s[i]; k++)if (j >= w[i][k])dp[j] = max(dp[j], dp[j - w[i][k]] + v[i][k]);cout << dp[m] << "\n";return 0;
}
总结
我们可以用一个公式来表示01背包、完全背包和多重背包:
dp[i][j]=max0≤k≤tdp[i−1][j−k⋅w[i]]+k⋅v[i],t={min(1,j/w[i]),01背包min(+∞,j/w[i])=j/w[i],完全背包min(s[i],j/w[i]),多重背包dp[i][j]=\max_{0\leq k\leq t} dp[i-1][j-k\cdot w[i]]+k\cdot v[i],\quad t=\begin{cases} \min(1,\;j/w[i]),&01背包\\ \min(+\infty,\;j/w[i])=j/w[i],&完全背包 \\ \min(s[i],\;j/w[i]),&多重背包 \end{cases} dp[i][j]=0≤k≤tmaxdp[i−1][j−k⋅w[i]]+k⋅v[i],t=⎩⎨⎧min(1,j/w[i]),min(+∞,j/w[i])=j/w[i],min(s[i],j/w[i]),01背包完全背包多重背包
相关文章:

动态规划专题——背包问题
🧑💻 文章作者:Iareges 🔗 博客主页:https://blog.csdn.net/raelum ⚠️ 转载请注明出处 目录前言一、01背包1.1 使用滚动数组优化二、完全背包2.1 使用滚动数组优化三、多重背包3.1 使用二进制优化四、分组背包总结…...

数据的分组聚合
1:分组 t.groupby #coding:utf-8 import pandas as pd import numpy as np file_path./starbucks_store_worldwide.csv dfpd.read_csv(file_path) #print(df.head(1)) #print(df.info()) groupeddf.groupby(byCountry) print(grouped) #DataFrameGroupBy #可以遍历…...
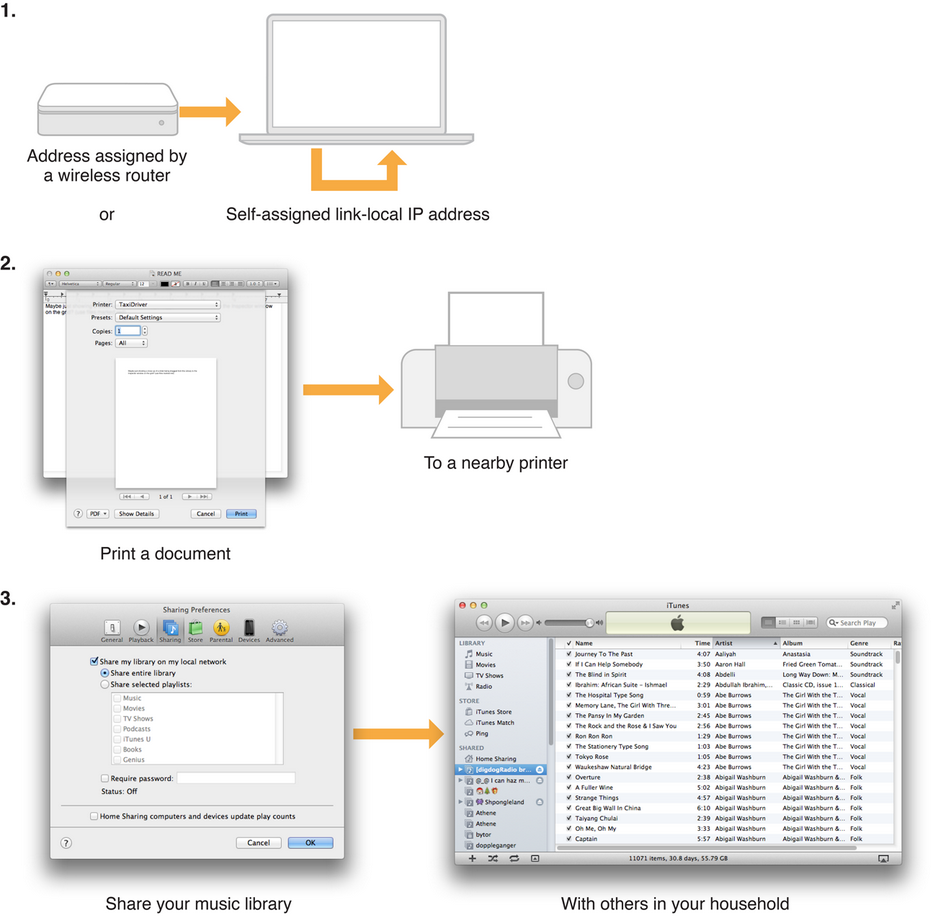
【Airplay_BCT】Bonjour conformance tests苹果IOT
从Airplay开始,接触到BCT,这是什么?被迫从安卓变成ios用户和开发。。。开始我的学习之旅,记录成长过程,不定时更新 Bonjour 下面是苹果官网关于bonjour的解释 Bonjour, also known as zero-configuration networking, …...
开发微服务电商项目演示(五)
登录方式调整第1步:从zmall-common的pom.xml中移除spring-session-data-redis依赖注意:本章节中不采用spring-session方式,改用redis直接存储用户登录信息,主要是为了方便之后的jmeter压测;2)这里只注释调用…...

Git删除大文件历史记录
Git删除大文件历史记录 git clone 仓库地址 查看大文件并排序 git rev-list --objects --all |grep $(git verify-pack -v .git/objects/pack/pack-*.idx | sort -k 3 -g | tail -1|awk {print $1})删除大文件 git filter-branch --force --index-filter git rm --cached --ig…...
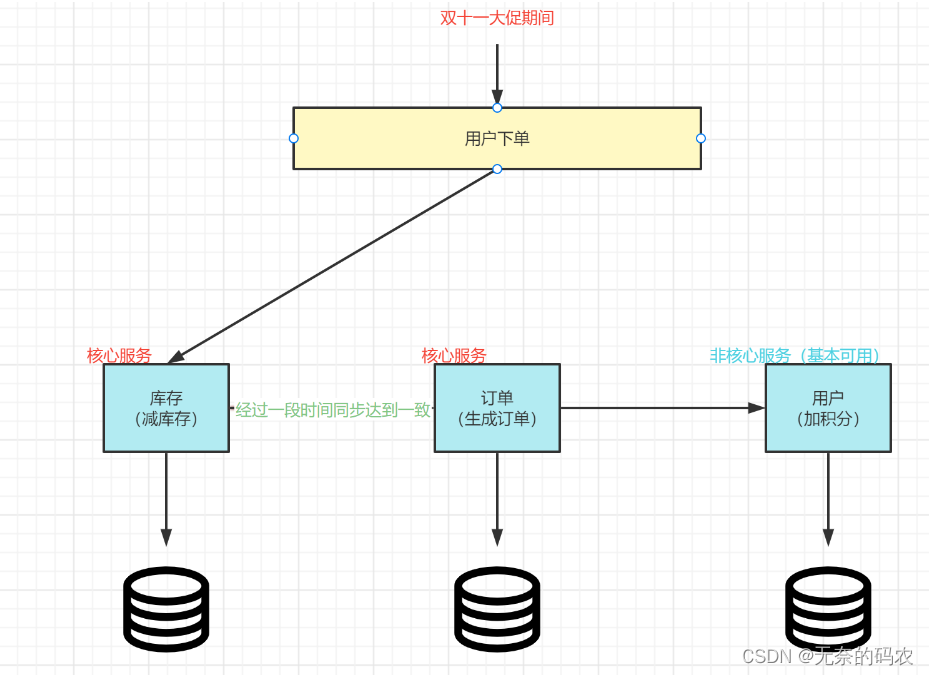
Seata-Server分布式事务原理加源码(一) - 微服务之分布式事务原理
概念 基础概念:事务ACID • A(Atomic):原子性,构成事务的所有操作,要么都执行完成,要么全部不执行,不可能出现部分成功部分失 败的情况。 • C(Consistency)…...

【ZooKeeper】zookeeper源码9-ZooKeeper读写流程源码分析
源码项目zookeeper-3.6.3:核心工作流程ZooKeeper选举和状态同步结束之后的服务启动ZooKeeper SessionTracker启动和工作机制ZooKeeper选举和状态同步结束之后的服务启动 在Leader的lead()方法的最后,即Leader完成了和集群过半Follower的同步之后&#x…...

Python实现批量导入xlsx数据1000条
遇到的问题:用户批量导入数据1000条,导入不成功的问题,提示查询不到商品资料。这个场景需要依靠批量的数据,每次测试的时候需要手动生成批量的数据,然后再导入操作,费时费劲。所以写了个脚本来实现。在前面…...
Ubuntu20.04安装redis与远程连接
一、安装Redis5.7 1、安装Redis apt-get install redis-server2、安装完成后,Redis服务器会自动启动。查看redis是否启动成功 service redis-server status #查看状态如下显示Active:active(running)状态:表示redis已在运行,启动成功。 …...

SAS应用入门学习笔记5
input 操作符: 代码说明: 1)1 表示第1列字符;7表示第7列字符; 2)col1 表示第一列数据;col2 表示第二列数据; 3)4.2 表示的是4个字符,2表示小数点后两位&a…...
PHP新特性集合
php8新特性命名参数function foo(string $a, string $b, ?string $c null, ?string $d null) { /* … */ }你可以通过下面的方式传入参数进行调用foo(b: value b, a: value a, d: value d, );联合类型php7class Number {/** var int|float */private $number;/*** param f…...
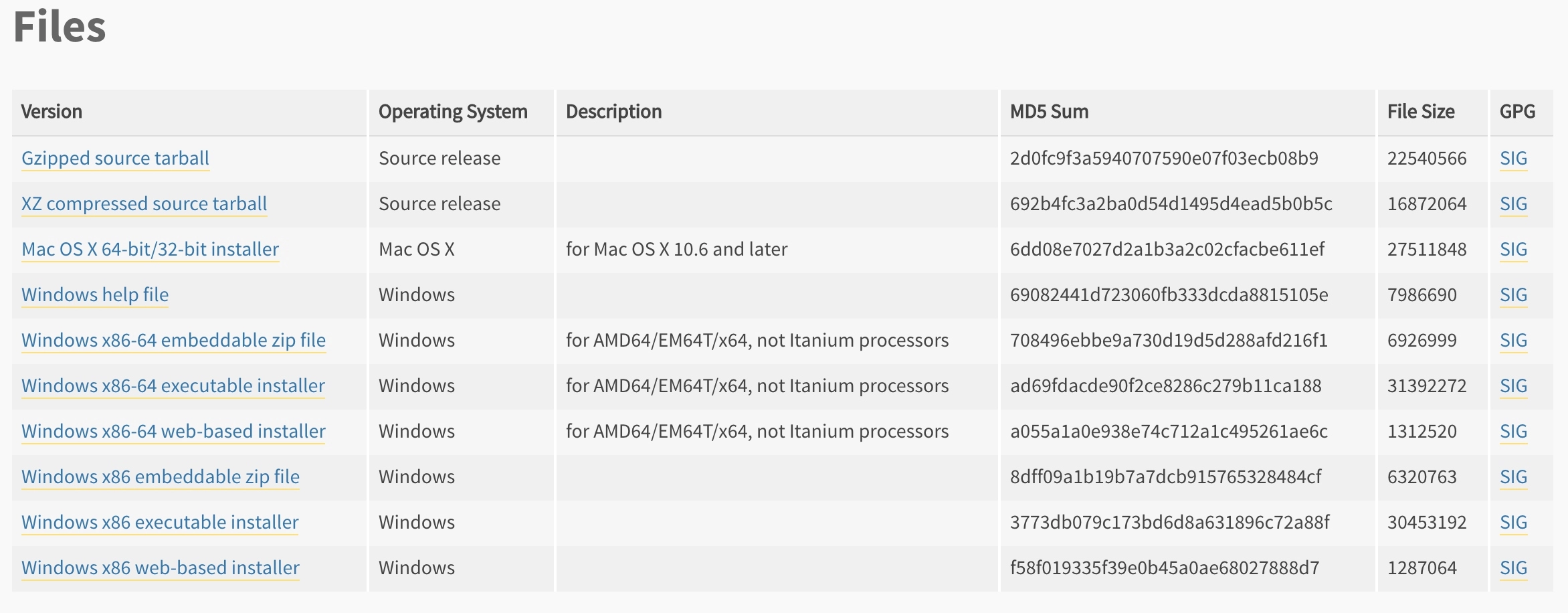
【开发环境配置】--Python3的安装
1-开发环境配置 工欲善其事,必先利其器! 编写和运行程序之前,我们必须先把开发环境配置好。只有配置好了环境并且有了更方便的开发工具,我们才能更加高效地用程序实现相应的功能。然而很多情况下,我们可能在最开始就…...

postman实现接口测试详细教程
各位小伙伴大家好, 今天为大家带来postman实战接口测试详细教程 一、通过接口文档集合抓包分析接口 通过fiddler抓包获取到注册接口URL地址及相关参数数据,并通过接口文档分析接口参数内容及参数说明, 如有必要的依赖条件必须进行梳理, 如token等 Fiddler抓包注册接口请求与…...
使用crontab执行定时任务
本来这个东西是挺简单的,是我脑子一直没转过来弯,我就想看看有多少人跟我一样😏 crontab语法自己去菜鸟教程看看就知道了,没什么难度 需求:每分钟定时执行一个PHP文件或者一个PHP命令 这是需要执行的文件࿰…...
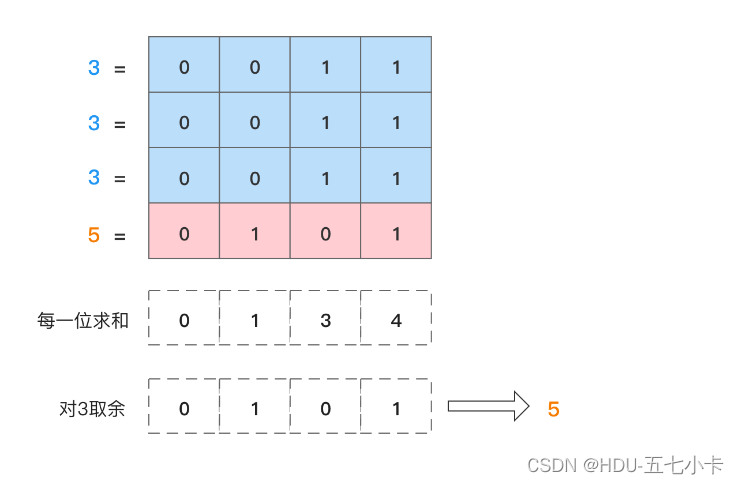
剑指 Offer 56 - II. 数组中数字出现的次数 II
题目 在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。 思路 这题是剑指 Offer 56 - I. 数组中数字出现的次数的变体,本题只有一个数num出现一次,其余的均出现三次 三次的话使用异或消无法…...

C语言学习笔记(八): 自定义数据类型
结构体变量 什么是结构体 C语言允许用户自己建立由不同类型数据组成的组合型的数据结构,它称为结构体 结构体的成员可以是任何类型的变量,如整数,字符串,浮点数,其他结构体,指针等 struct Student //s…...

Video Speed Controller谷歌视频加速插件——16倍速
文章目录前言最简单的版本一、如果是简单的话 可以Microsoft Edge使用二、简单的版本 火狐的话使用Global Speed插件三、由于视频受限以上的方法行不通 还是谷歌好用前言 主要是网课刷的时候 太慢所以找到了刷视频的方法 由于前几个的权限受限制 所以还是选用了谷歌浏览器的 V…...

VSCode 的下载安装及基本使用
目录 一、VSCode 是什么? 二、VSCode 的下载和安装 2.1 - 下载 2.2 - 安装 2.3 - 安装汉化插件 三、MinGW-w64 的下载安装及配置 3.1 - 介绍 3.2 - 下载 3.3 - 解压安装 3.4 - 环境变量配置 3.5 - 验证配置是否成功 3.6 - 安装 C/C 插件 四、在 VSCode …...

【操作系统】磁盘IO常见性能指标和分析工具实战
1.磁盘读写常见的指标 (1)IOPS(Input/Output Operations per Second) 指每秒能处理的I/O个数,表示块存储处理读写(输出/输入)的能力,单位为次,有顺序IOPS和随机IOPS比如…...

SpringMVC基础
简介 Spring MVC 属于 SpringFrameWork 的后续产品,已经融合在 Spring Web Flow 里面;Spring 框架提供了构建 Web 应用程序的全功能 MVC 模块;使用 Spring 可插入的 MVC 架构,从而在使用Spring进行WEB开发时,可以选择…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
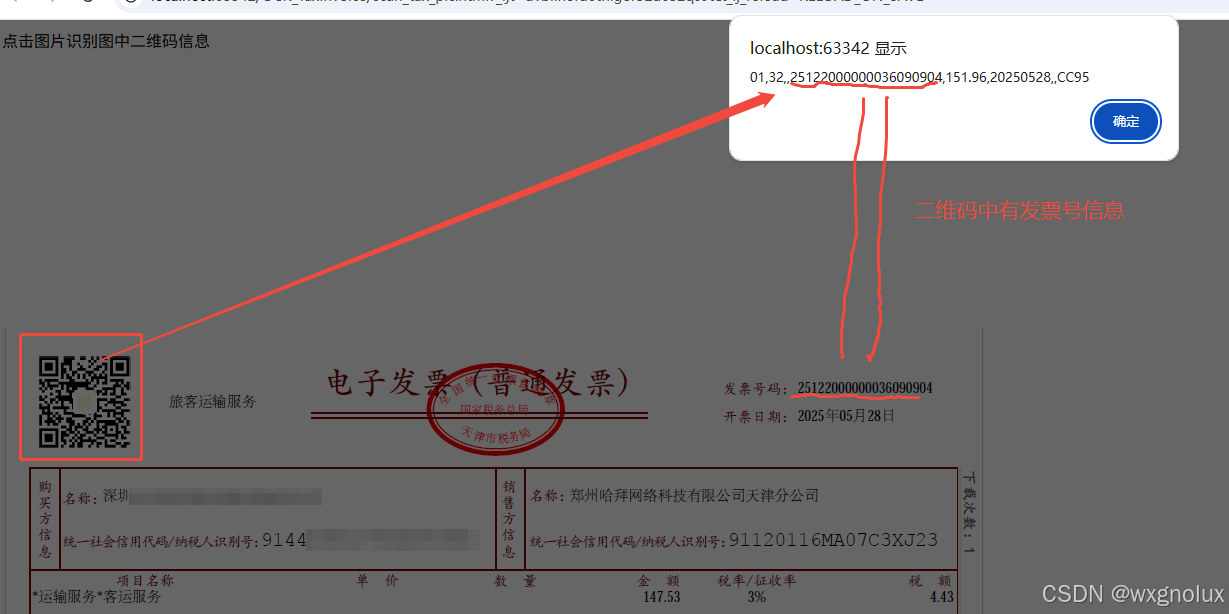
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
