【笔试】备战秋招,每日一题|20230415携程研发岗笔试
前言
最近碰到一个专门制作大厂真题模拟题的网站 codefun2000,最近一直在上面刷题。今天来进行2023.04.15携程研发岗笔试,整理了一下自己的思路和代码。
比赛地址
A. 找到you
题意:
给定一个仅包含小写字母的 n × n n\times n n×n 的矩阵,问这个矩阵中所有 2 × 2 2\times 2 2×2 的矩阵中同时包含 y、o 和 u 三个字符的子矩阵数量。
数据范围: 1 ≤ n , m ≤ 1000 1\leq n, m\leq 1000 1≤n,m≤1000
题解:
暴力枚举每个 2 × 2 2\times 2 2×2 子矩阵,对于每个子矩阵,判断其之中是否同时存在 y、o 和 u 三个字符即可,共需要枚举 ( n − 1 ) × ( m − 1 ) (n - 1) \times (m - 1) (n−1)×(m−1) 个子矩阵。
时间复杂度分析: O ( n m ) O(nm) O(nm)
#include <bits/stdc++.h>
using namespace std;const int N = 1010;
char s[N][N];
int n, m;bool check(int i, int j) {int val = 0;for (int x = 0; x < 2; ++x)for (int y = 0; y < 2; ++y) {if (s[i + x][y + j] == 'y') val |= 1 << 0;if (s[i + x][y + j] == 'o') val |= 1 << 1;if (s[i + x][y + j] == 'u') val |= 1 << 2;}return val == 7;
}int main()
{scanf("%d%d", &n, &m);;for (int i = 1; i <= n; ++i) scanf("%s", s[i] + 1);int ans = 0;for (int i = 1; i + 1 <= n; ++i)for (int j = 1; j + 1 <= m; ++j) {if (check(i, j)) ans += 1;}printf("%d\n", ans);return 0;
}
B. 最小公倍数
题意:
T T T 组数据,每组数据给定一个 n n n,现在问在 a + b = n a + b = n a+b=n 的情况下,使得 l c m ( a , b ) lcm(a, b) lcm(a,b) 最大的 a a a 和 b b b 是多少?
数据范围: 1 ≤ T ≤ 1 0 5 , 2 ≤ n ≤ 1 0 13 1\leq T\leq 10^5, 2\leq n\leq 10^{13} 1≤T≤105,2≤n≤1013
题解:
T T T 组数据,而 T T T 最大为 1 0 5 10^5 105 ,则每组数据至多要在 O ( log n ) O(\log n) O(logn) 的时间解决,因为这个题需要求 l c m lcm lcm,这个求解的复杂度是 O ( log n ) O(\log n) O(logn) 的,
所以判断的操作得在 O ( 1 ) O(1) O(1) 时间复杂度内。
下面我们都认为 a ≤ b a \leq b a≤b
当两个数 a a a 和 b b b ,满足 a + 1 = b a + 1 = b a+1=b ,那么此时 a a a 和 b b b 互质, l c m ( a , b ) = a × b lcm(a, b) = a \times b lcm(a,b)=a×b。
考虑奇数:将其拆分成 a = ⌊ n 2 ⌋ , b = ⌈ n 2 ⌉ a = \lfloor\frac{n}{2}\rfloor, b = \lceil\frac{n}{2}\rceil a=⌊2n⌋,b=⌈2n⌉,有 a + 1 = b a + 1 = b a+1=b,故此时最大的 l c m ( a , b ) lcm(a, b) lcm(a,b) 就是 a = ⌊ n 2 ⌋ , b = ⌈ n 2 ⌉ a = \lfloor\frac{n}{2}\rfloor, b = \lceil\frac{n}{2}\rceil a=⌊2n⌋,b=⌈2n⌉。
考虑偶数:将其拆分成 a = n 2 , b = n 2 a = \frac{n}{2}, b = \frac{n}{2} a=2n,b=2n 的 l c m ( a , b ) = n 2 lcm(a, b) = \frac{n}{2} lcm(a,b)=2n。
因为 n n n 是偶数,所以拆分出必然是要么 a a a 和 b b b 均为偶数,要么 a a a 和 b b b 均为奇数。
这里有一个结论,对于正数 a , b , n a,b,n a,b,n,如果有 a + b = n a + b = n a+b=n,且 a a a 和 b b b 均为奇数,则 g c d ( a , b ) = 1 gcd(a,b)=1 gcd(a,b)=1 。
当 n = 2 n=2 n=2,只有一种拆分法: a = 1 , b = 1 a=1,b=1 a=1,b=1。
当 n > 2 n>2 n>2,对于拆分 a = 1 , b = n − 1 , l c m ( 1 , n − 1 ) > l c m ( n 2 , n 2 ) a=1,b=n-1,lcm(1,n-1)>lcm(\frac{n}{2},\frac{n}{2}) a=1,b=n−1,lcm(1,n−1)>lcm(2n,2n),所以 a = n 2 , b = n 2 a=\frac{n}{2},b=\frac{n}{2} a=2n,b=2n这个拆分必然不如其他任意一个拆分。
此外,下面的讨论都只针对大于 2 2 2 的偶数。
所以对于一个数 n n n,我们至多只需要考虑 2 2 2 个位置,因为其他位置都不如这些位置中的任意一个:
当 n 2 \frac{n}{2} 2n 为奇数,
- a = n 2 − 1 , b = n 2 + 1 , l c m ( a , b ) = a × b g c d ( a , b ) = ( n 2 − 1 ) × ( n 2 + 1 ) 2 a = \frac{n}{2} - 1, b = \frac{n}{2} + 1, lcm(a,b)=\frac{a \times b}{gcd(a,b)}=\frac{(\frac{n}{2} - 1)\times (\frac{n}{2} + 1)}{2} a=2n−1,b=2n+1,lcm(a,b)=gcd(a,b)a×b=2(2n−1)×(2n+1),因为 b − a = 2 b-a=2 b−a=2,且 a a a 和 b b b 都是偶数,故 g c d ( a , b ) = 2 gcd(a,b)=2 gcd(a,b)=2
- a = n 2 − 2 , b = n 2 + 2 , l c m ( a , b ) = a × b g c d ( a , b ) = ( n 2 − 2 ) × ( n 2 + 2 ) 1 a = \frac{n}{2} - 2, b = \frac{n}{2} + 2,lcm(a,b)=\frac{a \times b}{gcd(a,b)}=\frac{(\frac{n}{2} - 2)\times (\frac{n}{2} + 2)}{1} a=2n−2,b=2n+2,lcm(a,b)=gcd(a,b)a×b=1(2n−2)×(2n+2),因为 b − a = 4 b-a=4 b−a=4,故公约数只能为 1 , 2 , 4 1,2,4 1,2,4,且 a a a 和 b b b 都是奇数,故最大公约数只能为 1 1 1。
当 n 2 \frac{n}{2} 2n 为偶数,
- a = n 2 − 1 , b = n 2 + 1 , l c m ( a , b ) = a × b g c d ( a , b ) = ( n 2 − 1 ) × ( n 2 + 1 ) 1 a = \frac{n}{2} - 1, b = \frac{n}{2} + 1, lcm(a,b)=\frac{a \times b}{gcd(a,b)}=\frac{(\frac{n}{2} - 1)\times (\frac{n}{2} + 1)}{1} a=2n−1,b=2n+1,lcm(a,b)=gcd(a,b)a×b=1(2n−1)×(2n+1),因为 b − a = 2 b-a=2 b−a=2,故公约数只能为 1 , 2 1, 2 1,2,且 a a a 和 b b b 都是奇数,故 g c d ( a , b ) = 1 gcd(a,b)=1 gcd(a,b)=1
- a = n 2 − 2 , b = n 2 + 2 , l c m ( a , b ) = a × b g c d ( a , b ) = ( n 2 − 2 ) × ( n 2 + 2 ) g c d ( a , b ) ≥ 2 a = \frac{n}{2} - 2, b = \frac{n}{2} + 2,lcm(a,b)=\frac{a \times b}{gcd(a,b)}=\frac{(\frac{n}{2} - 2)\times (\frac{n}{2} + 2)}{gcd(a,b)\geq2} a=2n−2,b=2n+2,lcm(a,b)=gcd(a,b)a×b=gcd(a,b)≥2(2n−2)×(2n+2),因为 b − a = 4 b-a=4 b−a=4,故公约数只能为 1 , 2 , 4 1,2,4 1,2,4,且 a a a 和 b b b 都是偶数,故最大公约数至少为 2 2 2。
上面已经说明了,对于本题中的 a + b = n a+b=n a+b=n, a × b > ( a − 1 ) × ( b + 1 ) = a × b + a − b − 1 a \times b > (a - 1) \times (b + 1) = a \times b + a - b - 1 a×b>(a−1)×(b+1)=a×b+a−b−1
因为 a − b − 1 < 0 a - b - 1 < 0 a−b−1<0,故 a × b > ( a − 1 ) × ( b + 1 ) a \times b > (a - 1) \times (b + 1) a×b>(a−1)×(b+1)。
当 n 2 \frac{n}{2} 2n 为奇数,
l c m ( n 2 − 1 , n 2 + 1 ) − l c m ( n 2 − 2 , n 2 + 2 ) = ( n 2 8 − 1 2 ) − ( n 2 4 − 4 ) = 28 − n 2 8 lcm(\frac{n}{2}-1,\frac{n}{2}+1)-lcm(\frac{n}{2}-2,\frac{n}{2}+2)=(\frac{n^2}{8}-\frac{1}{2})-(\frac{n^2}{4}-4)=\frac{28-n^2}{8} lcm(2n−1,2n+1)−lcm(2n−2,2n+2)=(8n2−21)−(4n2−4)=828−n2,因为 n 2 \frac{n}{2} 2n 为奇数且 n > 2 n>2 n>2,故 n ≥ 6 n\geq6 n≥6,故 28 − n 2 8 < 0 \frac{28-n^2}{8}<0 828−n2<0,故 l c m ( n 2 − 2 , n 2 + 2 ) > l c m ( n 2 − 1 , n 2 + 1 ) lcm(\frac{n}{2}-2,\frac{n}{2}+2)>lcm(\frac{n}{2}-1,\frac{n}{2}+1) lcm(2n−2,2n+2)>lcm(2n−1,2n+1)
当 n 2 \frac{n}{2} 2n 为偶数,
l c m ( n 2 − 1 , n 2 + 1 ) > l c m ( n 2 − 2 , n 2 + 2 ) lcm(\frac{n}{2}-1,\frac{n}{2}+1)>lcm(\frac{n}{2}-2,\frac{n}{2}+2) lcm(2n−1,2n+1)>lcm(2n−2,2n+2)
总结:
当 n n n 为奇数: a = ⌊ n 2 ⌋ , b = ⌈ n 2 ⌉ a = \lfloor\frac{n}{2}\rfloor, b = \lceil\frac{n}{2}\rceil a=⌊2n⌋,b=⌈2n⌉
当 n n n 为偶数:
- 当 n = 2 n = 2 n=2, a = 1 , b = 1 a=1,b=1 a=1,b=1
- 当 n 2 \frac{n}{2} 2n 为奇数, a = n 2 − 2 , b = n 2 + 2 a = \frac{n}{2} - 2, b = \frac{n}{2} + 2 a=2n−2,b=2n+2
- 当 n 2 \frac{n}{2} 2n 为偶数, a = n 2 − 1 , b = n 2 + 1 a = \frac{n}{2} - 1, b = \frac{n}{2} + 1 a=2n−1,b=2n+1
代码:
#include <bits/stdc++.h>
using namespace std;typedef long long ll;void solve() {ll n; scanf("%lld", &n);if (n & 1) {printf("%lld %lld\n", n / 2, n - n / 2);} else {if (n == 2) puts("1 1\n");if ((n / 2) & 1) {printf("%lld %lld\n", n / 2 - 2, n / 2 + 2);} else {printf("%lld %lld\n", n / 2 - 1, n / 2 + 1);}}}int main()
{int T;scanf("%d", &T);while (T--) {solve();}return 0;
}
C.魔法之树
题意:
给定一个 n n n 个点的树,问这棵树上任意一条简单路径,有起点和终点,这条路径上的点构成的二进制字符串对应的十进制数在 [ l , r ] [l, r] [l,r] 范围内的简单路径数。这里的简单路径长度至少为 1 1 1 ,即自己到自己不算在内
数据范围: 1 ≤ n ≤ 1000 , 1 ≤ l ≤ r ≤ 1 0 14 1\leq n\leq 1000, 1\leq l\leq r\leq {10^{14}} 1≤n≤1000,1≤l≤r≤1014
题解:
枚举以每个点作为起点,遍历完所有的其他 n − 1 n-1 n−1 个点为终点,当遇到值大于 r r r ,则后面的点作为终点的简单路径构成的二进制字符串对应的十进制数都必然大于 r r r 了,不会再可能成为答案了。这里必须要及时判断,一方面可以剪枝,另一方面是为了避免爆 long long。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
代码:
#include <bits/stdc++.h>
using namespace std;typedef long long ll;const int N = 1010;
vector<int> g[N];
int n;
ll l, r;
char s[N];
int ans;void dfs(int cur, int u, int fa, ll val) {val = val * 2 + (s[u] - '0');if (val > r) return ;if (val >= l && u != cur) ans += 1;for (int v: g[u]) {if (v == fa) continue ;dfs(cur, v, u, val);}
}void solve() {scanf("%d%lld%lld", &n, &l, &r);scanf("%s", s + 1);for (int i = 1; i < n; ++i) {int a, b;scanf("%d%d", &a, &b);g[a].push_back(b);g[b].push_back(a);}ans = 0;for (int i = 1; i <= n; ++i) {dfs(i, i, 0, 0);}printf("%d\n", ans);
}int main()
{int T = 1;
// scanf("%d", &T);while (T--) {solve();}return 0;
}
D.01串的回文子串
题意:
给定 n n n 个数 a i a_i ai,当 i i i 为奇数,表示生成 a i a_i ai 个 1,当 i i i 为偶数,表示生成 a i a_i ai 个 0。即生成一个长度为 ∑ i = 1 n a i \sum\limits_{i=1}^n a_i i=1∑nai 的序列 s s s, s [ 1 , a 1 ] = 1 , s [ a 1 + 1 , a 2 ] = 0 , s [ a 2 + 1 , a 3 ] = 1 , s [ a 3 + 1 , a 4 ] = 0 , . . . s[1, a_1]=1,s[a_1+1,a_2]=0,s[a_2+1,a_3]=1,s[a_3+1,a_4]=0,... s[1,a1]=1,s[a1+1,a2]=0,s[a2+1,a3]=1,s[a3+1,a4]=0,... 。问这个序列中有多少个回文子串。答案对 1 0 9 + 7 10^9+7 109+7 取模
数据范围:
1 ≤ n ≤ 1000 , 1 ≤ a i ≤ 1 0 9 1\leq n\leq 1000,1\leq a_i\leq 10^9 1≤n≤1000,1≤ai≤109
题解:
可以将看成序列看成分为 n n n 块,每块内部都是连续的 0 0 0 或 1 1 1。
考虑每块内部可以生成多少回文子串:一块内部有 x x x 个数,以第 i i i 个数结尾的回文子串数量为 i i i ,即 ∑ i = 1 x i = x × ( x + 1 ) 2 \sum\limits_{i=1}^xi=\frac{x\times (x+1)}{2} i=1∑xi=2x×(x+1)
再考虑包含第 i i i 块的回文子串数量。那么以第 i i i 块为回文子串中心,向左右扩展。当且仅当左右两个数都相同,会多生成一个回文子串。这个什么时候截止呢,假设我们当前 a [ i − 1 ] = a [ i + 1 ] , a [ i − 2 ] = a [ i + 2 ] , . . . a [ i − p ] = a [ i + p ] a[i-1]=a[i+1],a[i-2]=a[i+2],...a[i-p]=a[i+p] a[i−1]=a[i+1],a[i−2]=a[i+2],...a[i−p]=a[i+p],但是 a [ i − p − 1 ] ≠ a [ i + p + 1 ] a[i-p-1]\neq a[i+p+1] a[i−p−1]=a[i+p+1],则生成的回文子串数为: m i n ( a [ i − p − 1 ] , a [ i + p + 1 ] ) + ∑ j = 1 p a [ j ] min(a[i-p-1],a[i+p+1])+\sum\limits_{j=1}^p a[j] min(a[i−p−1],a[i+p+1])+j=1∑pa[j]
时间复杂度: O ( n 2 ) O(n^2) O(n2)
代码:
#include <bits/stdc++.h>
using namespace std;const int N = 1010;
const int mod = 1e9 + 7;long long a[N];
int n;void solve() {long long ans = 0;scanf("%d", &n);for (int i = 1; i <= n; ++i) {scanf("%lld", &a[i]);ans = (ans + a[i] * (a[i] + 1) / 2) % mod;}for (int i = 2; i < n; ++i) {int L = i - 1, R = i + 1;while (L >= 1 && R <= n) {ans = (ans + min(a[L], a[R])) % mod;if (a[L] == a[R]) L -= 1, R += 1;else break;}}printf("%lld\n", ans);
}int main()
{int T = 1;
// scanf("%d", &T);while (T--) {solve();}return 0;
}
相关文章:

【笔试】备战秋招,每日一题|20230415携程研发岗笔试
前言 最近碰到一个专门制作大厂真题模拟题的网站 codefun2000,最近一直在上面刷题。今天来进行2023.04.15携程研发岗笔试,整理了一下自己的思路和代码。 比赛地址 A. 找到you 题意: 给定一个仅包含小写字母的 n n n\times n nn 的矩阵…...
【unity专题篇】—GUI(IMGUI)思维导图详解
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...

【C++ Metaprogramming】0. 在C++中实现类似C#的泛型类
两年前,笔者因为项目原因刚开始接触C,当时就在想,如果C有类似C#中的泛型限定就好了,能让代码简单许多。我也一度认为: 虽然C有模板类,但是却没办法实现C#中泛型特有的 where 关键词: public c…...
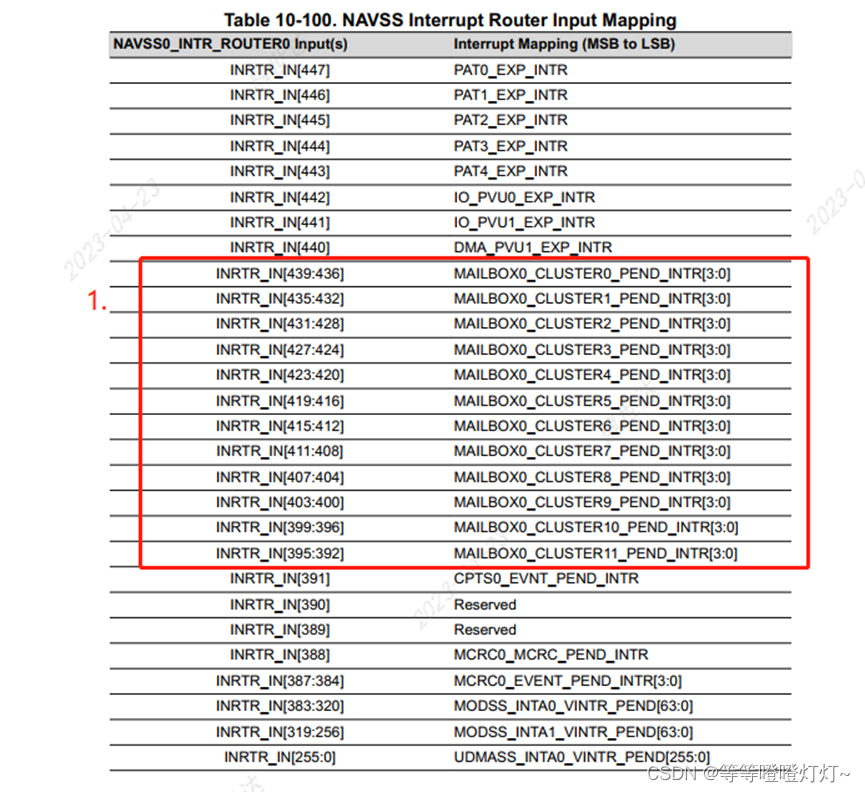
TDA4VM/VH 芯片 NAVSS0
请从官网下载 TD4VM 技术参考手册,地址如下: TDA4VM 技术参考手册地址 概述 (NAVSS0 的介绍在 TRM 的第10.2章节) NAVSS0 可以看作 MAIN 域的一个复杂外设域,实现如下功能: UDMASS: DMA 管理子系统;MODSS…...

基于springboot的前后端分离的案列(一)
SpringBootWeb案例 前面我们已经讲解了Web前端开发的基础知识,也讲解了Web后端开发的基础(HTTP协议、请求响应),并且也讲解了数据库MySQL,以及通过Mybatis框架如何来完成数据库的基本操作。 那接下来,我们就通过一个案例…...
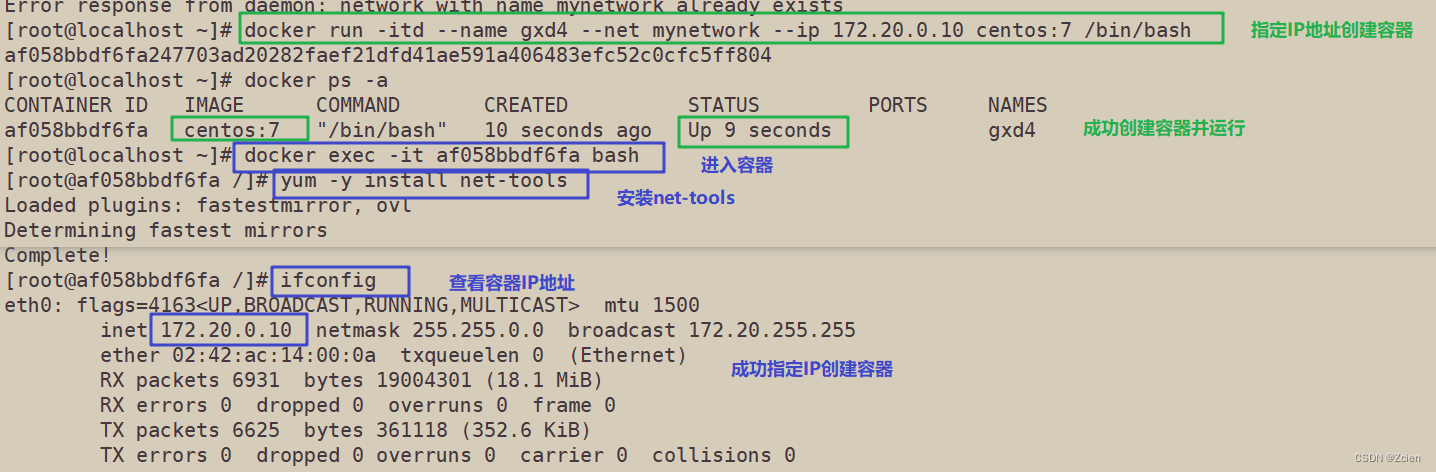
Docker网络模式详解
文章目录 一、docker网络概述1、docker网络实现的原理1.1 随机映射端口( 从32768开始)1.2 指定映射端口1.3 浏览器访问测试 二、 docker的网络模式1、默认网络2、使用docker run 创建Docker容器时,可以用--net或--network 选项指定容器的网络模式 三、docker网络模式…...
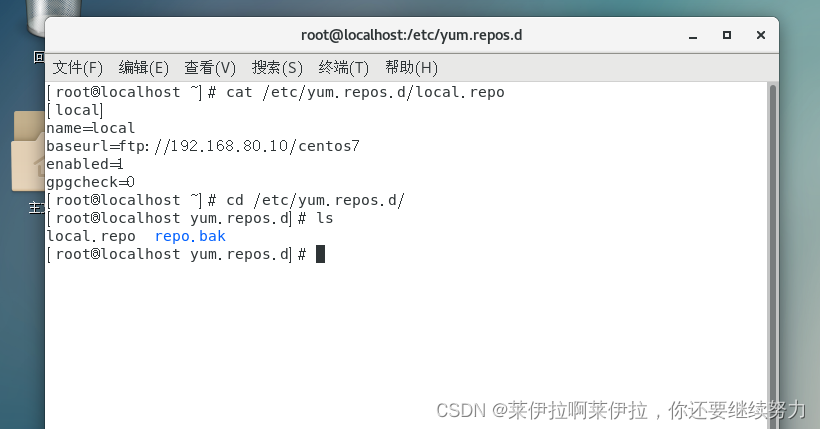
PXE高效批量网络装机
PXE 定义 PXE(预启动执行环境,在操作系统之前运行)是由Intel公司开发的网络引导技术,工作在client /server模式,允许客户机通过网络从远程服务器下载引导镜像,并加载安装文件或者整个操作系统。 具备以下三个优点 1 规模化: 同时…...

YOLOv5+双目实现三维跟踪(python)
YOLOv5双目实现三维跟踪(python) 1. 目标跟踪2. 测距模块2.1 测距原理2.2 添加测距 3. 细节修改(可忽略)4. 实验效果 相关链接 1. YOLOV5 双目测距(python) 2. YOLOV7 双目测距(python&#x…...

ESP8266使用SDK软硬件定时执行函数
1、软件定时 以下接口使用的定时器由软件实现,定时器的函数在任务中被执行。因为任务可能被中断,或者被其他高优先级的任务延迟,因此以下os_timer系列的接口并不能保证定时器精确执行。 注意: ①对于同一个 timer,os…...
ThreadPoolExecutor源码阅读流程图
1.创建线程池 public ThreadPoolExecutor(int corePoolSize,int maximumPoolSize,long keepAliveTime,TimeUnit unit,BlockingQueue<Runnable> workQueue) {this(corePoolSize, maximumPoolSize, keepAliveTime, unit, workQueue,Executors.defaultThreadFactory(), def…...

如何通过筛选高质量爬虫IP提升爬虫效率?
前言 对于做数据抓取的技术员来说,如何稳定高效的爬取数据ip库池起到决定性作用,对于爬虫ip池的维护,可以从以下几个方面入手: 目录 一、验证爬虫ip的可用性二、更新爬虫ip池三、维护爬虫ip的质量四、监控爬虫ip的使用情况 一、验…...

C#中定义数组--字符串及数组操作
C#中定义数组–字符串及数组操作 以前用VB的时候经常使用数组,不过C#用习惯后数组基本上用的不多了。 像用List<>,ArrayList,Dirctionary<,>都比较好用。 一、一维: int[] numbers new int[]{1,2,3,4,5,6}; //不…...
嵌入式就业怎么样?
嵌入式就业怎么样? 现在的IT行业,嵌入式是大热门,下面也要来给大家介绍下学习嵌入式之后的发展以及就业怎么样。 首先是好找工作。嵌入式人才目前是处于供不应求的状态中,据权威统计机构统计在所有软件开发类人才的需求中,对嵌入式工程师的…...
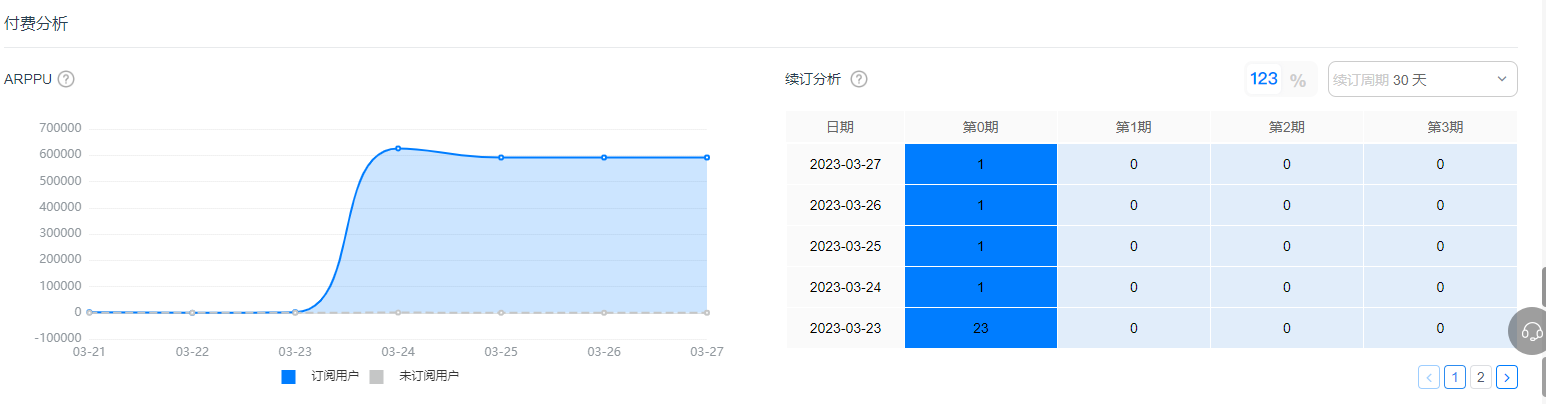
用户订阅付费如何拆解分析?看这篇就够了
会员制的订阅付费在影音娱乐行业中已相当普及,近几年,不少游戏厂商也开始尝试订阅收费模式。在分析具体的用户订阅偏好以及订阅付费模式带来的增长效果时,我们常常会有这些疑问: 如何从用户的整体付费行为中具体拆解订阅付费事件…...

智能合约中如何调用其他智能合约
智能合约是区块链技术中的一项关键功能,它可以让开发者编写代码来自动执行一系列的操作,从而实现各种复杂的业务逻辑。在许多应用场景中,一个智能合约可能需要调用另一个智能合约来完成某些任务。本文将介绍智能合约如何调用其他智能合约&…...

python的多任务处理
在现代计算机系统中,多任务处理是一项重要的技术,可以大幅提高程序的运行效率。Python语言提供了多种多任务处理的方式,本文将介绍其中几种常见的方式,包括多进程、多线程和协程。 多进程 进程是计算机中运行程序的实例…...

Vue收集表单数据学习笔记
收集表单数据 v-model双向数据绑定,收集的是input框的value,单选按钮不存在value,就像代码中的男女选项,即使绑定性别v-model“sex”,控制台依然不能接收性别的值,因为没有value值,,…...
Linux搭建GitLab私有仓库,并内网穿透实现公网访问
文章目录 前言1. 下载Gitlab2. 安装Gitlab3. 启动Gitlab4. 安装cpolar5. 创建隧道配置访问地址6. 固定GitLab访问地址6.1 保留二级子域名6.2 配置二级子域名 7. 测试访问二级子域名 转载自远控源码文章:Linux搭建GitLab私有仓库,并内网穿透实现公网访问 …...

SpringBoot项目防重复提交注解开发
背景 在实际开发过程中,防重复提交的操作很常见。有细分配置针对某一些路径进行拦截,也有基于注解去实现的指定方法拦截的。 分析 实现原理 实现防重复提交,我们很容易想到就是用过滤器或者拦截器来实现。 使用拦截器就是继承HandlerInt…...

从软件哲学角度谈 Amazon SageMaker
如果你喜欢哲学并且你是一个 IT 从业者,那么你很可能对软件哲学感兴趣,你能发现存在于软件领域的哲学之美。本文我们就从软件哲学的角度来了解一下亚马逊云科技的拳头级产品 Amazon SageMaker,有两个出发点:一是 SageMaker 本身设…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
