Latex常用符号和功能记录
公式下括号
\underbrace & \overbrace
\begin{equation}
\underbrace{L_1+L_2}_{loss ~ 1} + \overbrace{L_3+L_4}^{loss ~ 2}
\end{equation}
L = L 1 + L 2 ⏟ l o s s 1 + L 3 + L 4 ⏞ l o s s 2 L = \underbrace{L_1+L_2}_{loss ~ 1} + \overbrace{L_3+L_4}^{loss ~ 2} L=loss 1 L1+L2+L3+L4 loss 2
矩阵
\begin{equation}
f =
\left[
\begin{array}{ccc}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}
\right]
\end{equation}
f = [ 1 1 1 1 1 1 1 1 1 ] f={\left[ \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array} \right] } f= 111111111
乘法
$\odot$
$\otimes$
⊙ \odot ⊙
⊗ \otimes ⊗
相关文章:

Latex常用符号和功能记录
公式下括号 \underbrace & \overbrace \begin{equation} \underbrace{L_1L_2}_{loss ~ 1} \overbrace{L_3L_4}^{loss ~ 2} \end{equation}L L 1 L 2 ⏟ l o s s 1 L 3 L 4 ⏞ l o s s 2 L \underbrace{L_1L_2}_{loss ~ 1} \overbrace{L_3L_4}^{loss ~ 2} Lloss 1…...
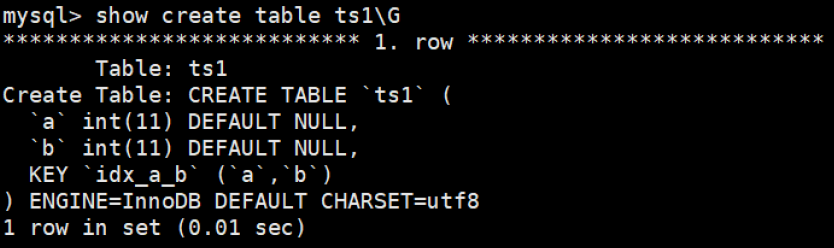
MySQL高级篇——索引的创建与设计原则
导航: 【黑马Java笔记踩坑汇总】JavaSEJavaWebSSMSpringBoot瑞吉外卖SpringCloud黑马旅游谷粒商城学成在线牛客面试题 目录 一、索引的分类与使用 1.1 索引的分类 1.1.1. 普通索引 1.1.2. 唯一性索引 1.1.3. 主键索引(唯一非空) 1.1.4…...

王一茗: “大数据能力提升项目”与我的成长之路 | 提升之路系列(三)
导读 为了发挥清华大学多学科优势,搭建跨学科交叉融合平台,创新跨学科交叉培养模式,培养具有大数据思维和应用创新的“π”型人才,由清华大学研究生院、清华大学大数据研究中心及相关院系共同设计组织的“清华大学大数据能力提升项…...
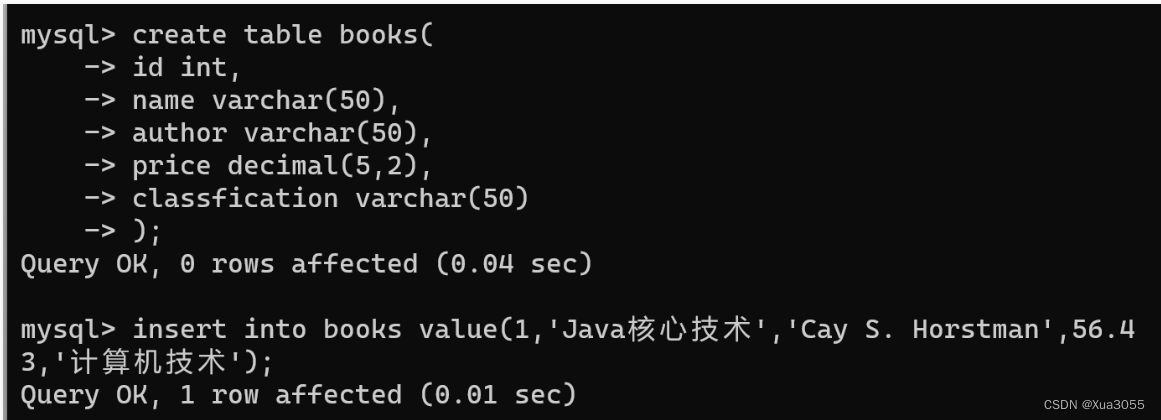
MySQL:数据库的基本操作
MySQL是一个客户端服务器结构的程序, 一.关系型数据库 关系型数据库是一个结构化的数据库,创建在关系模型(二维表格模型)基础上,一般面向于记录。 主流的关系型数据库包括 Oracle、MySQL、SQL Server、Microsoft Access、DB2 等. …...
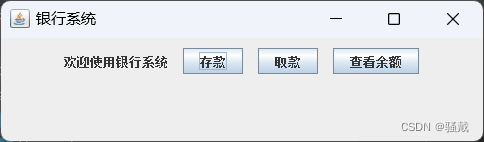
银行系统【GUI/Swing+MySQL】(Java课设)
系统类型 Swing窗口类型Mysql数据库存储数据 使用范围 适合作为Java课设!!! 部署环境 jdk1.8Mysql8.0Idea或eclipsejdbc 运行效果 本系统源码地址:https://download.csdn.net/download/qq_50954361/87708777 …...

【社区图书馆】-《科技服务与价值链》总结
【为什么研究价值链】 价值链及价值链协同体系是现代产业集群的核心枢纽,是推进城市群及产业集群化、服务化、生态化发展的纽带。因而推进价值链协同,创新发展价值链协同业务科技资源体系,既是科技服务业创新的重要方向,也是重塑生…...
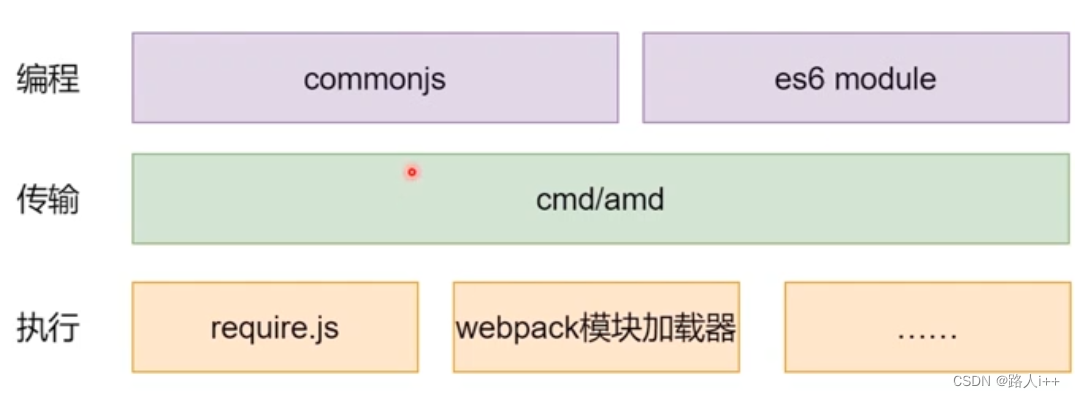
工具链和其他-异步模块加载
目录 CMD/AMD Asynchronous Module Definition(AMD异步模块定义,语法风格) Common Module Definition ES6/CommonJS CommonJS ES6 Module 加载器示例 总结 cmd和amd的区别 现在有哪些异步加载方式 整体结构 编程:commonjs es6 module (有可能解…...

第一次使用R语言
在R语言中,“<-”符号与“”意义一样。另一种奇怪的R语言的等号表示方法,是以“->”表示,但是用得少。 有些计算机语言,变量在使用前要先定义,R语言则不需先定义,可在程序中直接设定使用。 若在Con…...

《语文教学通讯》栏目 收稿范围
《语文教学通讯》创刊于1978年,是由山西师范大学主管,山西师大教育科技传媒集团主办的期刊。历年被人民大学书报资料中心转载、复印的篇幅数量均居同类报刊之首。国内刊号:CN 14-1017/G4,国际刊号:ISSN 1004-6097&…...

Towards Principled Disentanglement for Domain Generalization
本文用大量的理论论述了基于解纠缠约束优化的域泛化问题。 这篇文章认为以往的文章在解决域泛化问题时所用的方法都是non-trivial的,也就是说没有作严格的证明,是不可解释的,而本文用到大量的定理和推论证明了方法的有效性。 动机 因为域泛…...
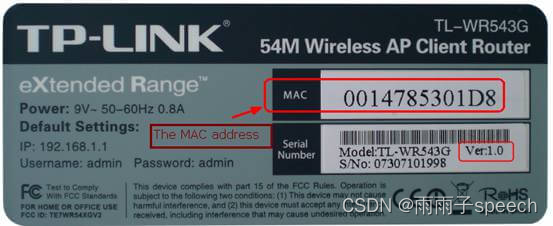
计算机网络学习02
1、TCP 与 UDP 的区别? 是否面向连接 : UDP 在传送数据之前不需要先建立连接。而 TCP 提供面向连接的服务,在传送数据之前必须先建立连接,数据传送结束后要释放连接。是否是可靠传输: 远地主机在收到 UDP 报文后&…...

网络交换机端口管理工具
如今,企业或组织级网络使用数百个交换机端口作为其 IT 基础架构的一部分来实现网络连接。这使得交换机端口管理成为日常网络管理任务的一部分。传统上,网络管理员必须依靠手动网络交换机端口管理技术来跟踪交换机及其端口连接状态。这种手动任务弊大于利…...

redis五大命令kv设计建议内存淘汰
什么是redis?主要作用? redis(remote dictionary server)远程字典服务:是一个开源的使用ANSI C语言编写,支持网络、可基于内存可持久化的日志型、key-value数据库,并提供多种语言的api redis的数据存在内存中ÿ…...
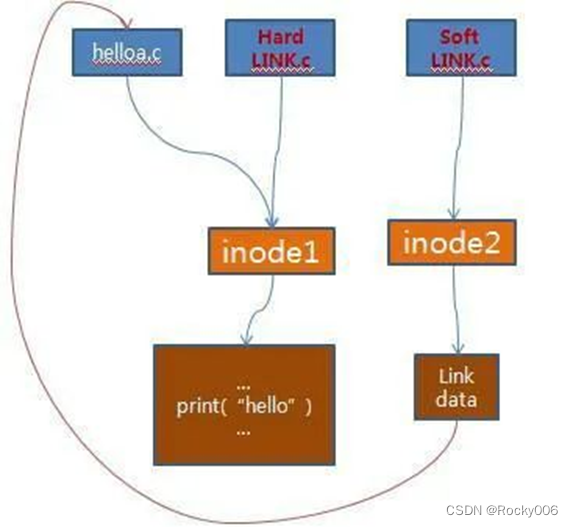
如何真正认识 Linux 系统结构?这篇文章告诉你
Linux 系统一般有 4 个主要部分:内核、shell、文件系统和应用程序。内核、shell 和文件系统一起形成了基本的操作系统结构,它们使得用户可以运行程序、管理文件并使用系统。 Linux内核 内核是操作系统的核心,具有很多最基本功能,…...
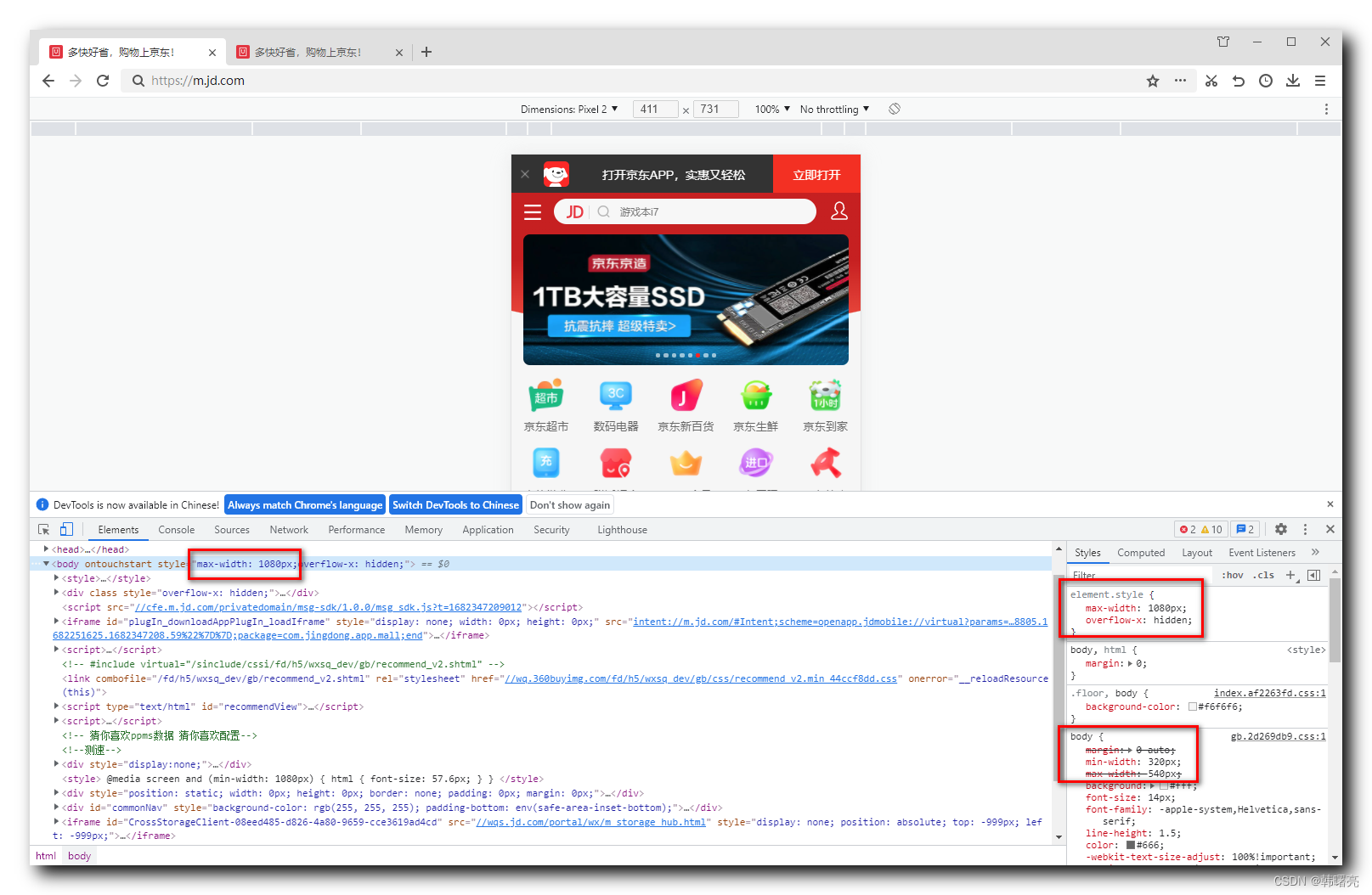
【移动端网页布局】流式布局案例 ① ( 视口标签设置 | CSS 样式文件设置 | 布局宽度设置 | 设置最大宽度 | 设置最小宽度 )
文章目录 一、视口标签设置二、CSS 样式文件设置三、布局宽度设置1、设置布局宽度2、设置布局最大宽度3、设置布局最小宽度4、查看网页最大最小宽度5、布局宽度设置 四、代码示例1、主界面标签2、CSS 布局设置 一、视口标签设置 参考 【移动端网页布局】移动端网页布局基础概念…...

力扣---LeetCode88. 合并两个有序数组
文章目录 前言88. 合并两个有序数组链接:方法一:三指针(后插)1.2 代码:1.2 流程图:方法二:开辟新空间2.1 代码:2.2 流程图:2.3 注意: 总结 前言 “或许你并不熠熠生辉甚至有点木讷但…...
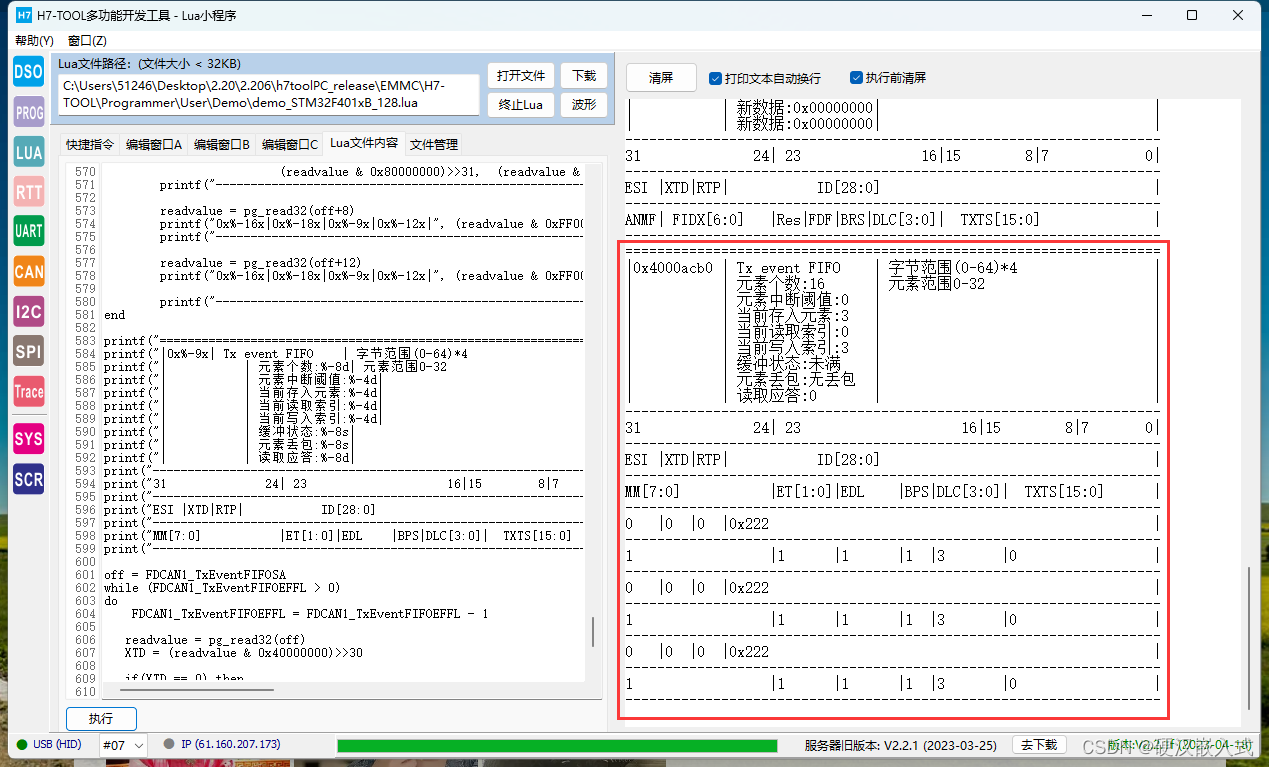
H7-TOOL的CANFD Trace全解析功能制作完成,历时一个月(2023-04-28)
为了完成这个功能,差不多耗费了一个月时间,精神状态基本已经被磨平了。 当前已经支持: 1、LUA小程序控制,使用灵活。 2、采用SWD接口直接访问目标板芯片的CANFD外设寄存器和CANFD RAM区实现,支持USB,以太网…...
探析Android中的四类性能优化
作者:Yj家的孺子牛 流畅性优化 主线程模型 了解 Android 的流畅性优化之前,我们需要先了解Android的线程结构。在 Android 中,有一个主线程模型,其中所有的绘制以及交互都是在主线程中进行的,所以,当我们…...

ubuntu18.04 安装编译zlmediakit
参考http://www.cherrylord.cn/archives/zlmediakit 1、获取代码 #国内用户推荐从同步镜像网站gitee下载 git clone --depth 1 https://gitee.com/xia-chu/ZLMediaKit cd ZLMediaKit #千万不要忘记执行这句命令 git submodule update --init#国内用户推荐…...
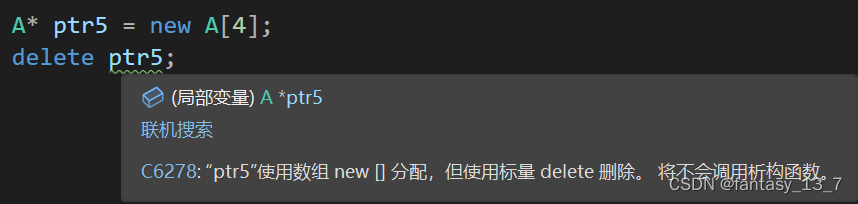
C++ -5- 内存管理
文章目录 C语言和C内存管理的区别示例1. C/C 中程序内存区域划分2. C中动态内存管理3.operator new 与 operator delete 函数4.new 和 delete 的实现原理5.定位new表达式 C语言和C内存管理的区别示例 //C语言: struct SListNode {int data;struct SListNode* next; …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
