枚举法计算24点游戏
# 请在此处编写代码
# 24点游戏
import itertools# 计算24点游戏代码
def twentyfour(cards):"""(1)itertools.permutations(可迭代对象):通俗地讲,就是返回可迭代对象的所有数学全排列方式。itertools.permutations("1118") -> 即将数字1118进行全排列组合(2)itertools.product(*iterables, repeat=1)iterables是可迭代对象,repeat指定iterable重复几次返回一个或者多个iterables中的元素的笛卡尔积的元组即为product(list1, list2) 依次取出list1中的每1个元素,与list2中的每1个元素,组成元组,repeat即为元组中有几个元素,最多重复几次(3)"""for num in itertools.permutations(cards):#提取数字for ops in itertools.product("+-*/", repeat=3):#提取运算符# ({0}{4}{1}){5}({2}{6}{3}) - > 即在{0}{1}{2}{3}放上数字,{4}{5}{6}放上运算符号,只能放三个,四个数字中间只能放三个运算符# 带括号有8种方法#带括号的意思是三个运算符的优先运算组成方式有8类# 1. (ab)cdbsd1 = '({0}{4}{1}){5}{2}{6}{3}'.format(*num, *ops)# 2. a(bc)dbsd2 = '{0}{4}({1}{5}{2}){6}{3}'.format(*num, *ops)# 3. ab(cd)bsd3 = '{0}{4}{1}{5}({2}{6}{3})'.format(*num, *ops)# 4. (ab)(cd)bsd4 = '({0}{4}{1}){5}({2}{6}{3})'.format(*num, *ops)# 5. ((ab)c)dbsd5 = '(({0}{4}{1}){5}{2}){6}{3}'.format(*num, *ops)# 6. (a(bc))dbsd6 = '({0}{4}({1}{5}{2})){6}{3}'.format(*num, *ops)# 7. a((bc)d)bsd7 = '{0}{4}(({1}{5}{2}){6}{3})'.format(*num, *ops)# 8. a(b(cd))bsd8 = '{0}{4}({1}{5}({2}{6}{3}))'.format(*num, *ops)# print([bsd1, bsd2, bsd3, bsd4, bsd5, bsd6, bsd7, bsd8])for bds in [bsd1, bsd2, bsd3, bsd4, bsd5, bsd6, bsd7, bsd8]:try:if abs(eval(bds) - 24.0) < 1e-20:return "24点结果 = "+bdsexcept ZeroDivisionError: # 零除错误continuereturn "Not fond"cards = ['2484', '1126', '1127', '1128', '2484', '1111']
for card in cards:print(twentyfour(card))总结:
1、了解了枚举算法注意事项
在列举的过程中,既不能遗漏也不要重复。
2、明晰了枚举算法的核心
itertools.permutations将输入的可迭代对象即四个数字进行所有可能的全排列;
for num in itertools.permutations(cards):#提取数字并排列itertools.product将设定好的List1即四个运算符中提取三个与repeat=3相对应;
for ops in itertools.product("+-*/", repeat=3):#提取运算符将提取的数字排列与运算符依次放入八种可能的优先运算方式中,如果可以满足24点游戏的规则那么输出结果,如果8种运算方式都无法成功得出结果那么就返回”not fond“。
3、学习了4个数字三个运算符的优先排列方式
共有八种:
(ab)cd、a(bc)d、ab(cd)、(ab)(cd)、((ab)c)d、(a(bc))d、a((bc)d)、a(b(cd))。
4、运算结果
| 输入数字 | 2484 | 1126 | 1127 | 1128 | 2484 | 1111 |
| 运算结果 | (2+4)*(8-4) | ((1+1)+2)*6 | (1+2)*(1+7) | (1+(1*2))*8 | (2+4)*(8-4) | not fond |
相关文章:

枚举法计算24点游戏
# 请在此处编写代码 # 24点游戏 import itertools# 计算24点游戏代码 def twentyfour(cards):"""(1)itertools.permutations(可迭代对象):通俗地讲,就是返回可迭代对象的所有数学全排列方式。itertools.permutations("1118") -…...

@Cacheable注解
Cacheable注解是Spring框架中提供的一种缓存技术, 用于标记一个方法的返回值可以被缓存起来,当再次调用该方法时,如果缓存中已经存在缓存的结果,则直接从缓存中获取结果而不是再次执行该方法,从而提高系统的性能和响应…...

CentOS分区挂载 fdisk、parted方式解析
1 介绍 在linux中,通常会将持久化数据保存到硬盘当中,但是硬盘一把会比较大,因此我们为了方便管理,会将一个硬盘分成多个逻辑硬盘,称之为分区。 为了能够让分区中的文件使得能让操作系统处理,则需要对分区…...

BuildKit
介绍 BuildKit是一个现代化的构建系统,主要用于构建和打包容器镜像。它是Docker官方的构建引擎,支持构建多阶段构建、缓存管理、并行化构建、多平台构建等功能。BuildKit还支持多种构建语法和格式,包括Dockerfile、BuildKit Build Specifica…...
c++ 11标准模板(STL) std::vector (二)
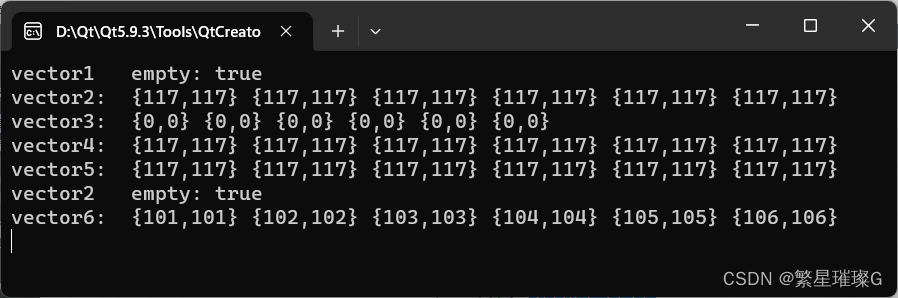
定义于头文件 <vector> template< class T, class Allocator std::allocator<T> > class vector;(1)namespace pmr { template <class T> using vector std::vector<T, std::pmr::polymorphic_allocator<T>>; }(2)(C17…...

Python 循环技巧
目录 在字典中循环时,用 items() 方法可同时取出键和对应的值: 在序列中循环时,用 enumerate() 函数可以同时取出位置索引和对应的值: 同时循环两个或多个序列时,用 zip() 函数可以将其内的元素一一匹配:…...

【Java笔试强训 7】
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🤺🤺🤺 目录 一、选择题 二、编程题 🔥Fibona…...
工作7年的程序员,明白了如何正确的“卷“
背景 近两年,出台和落地的反垄断法,明确指出要防止资本无序扩张。 这也就导致现在的各大互联网公司,不能再去染指其他已有的传统行业,只能专注自己目前存量的这些业务。或者通过技术创新,开辟出新的行业。 但创新这…...

数学建模——查数据
如果选择C题的小伙伴常常需要查找一些数据,那么这些数据一般都可以从哪里找到呢? 常用的查数据平台 优先在知网、谷歌学术等平台搜索国家统计局 最全面,月度季度年度,各地区各部门各行业,包罗万象 https://data.stat…...

PAT A1019 General Palindromic Number
1019 General Palindromic Number 分数 20 作者 CHEN, Yue 单位 浙江大学 A number that will be the same when it is written forwards or backwards is known as a Palindromic Number. For example, 1234321 is a palindromic number. All single digit numbers are pa…...
ChatGPT会颠覆SEO内容创作吗
近几年 AI 的发展日新月异。除了搜索算法本身大规模应用人工智能,我也一直关注着 AI 用于写作的进展。 上篇关于 Google 有用内容更新的帖子还在说,高质量内容创作是 SEO 最难的事之一,对某些网站来说,如果能有工具帮助ÿ…...
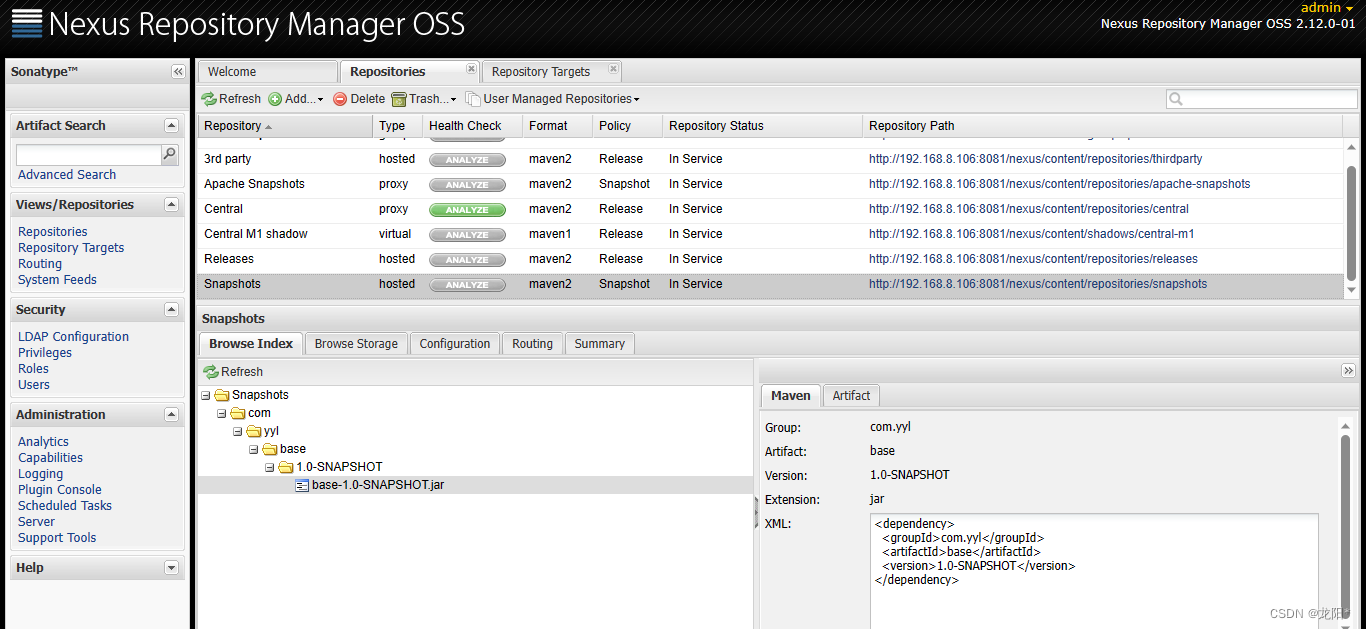
Maven私服搭建
为什么要搭建私服 通常在maven项目的pom.xml文件中引入了某个依赖包之后,maven首先会去本地仓库去搜索,本地仓库搜索不到会去maven的配置文件settings.xml中配置的maven镜像地址去找,比如: <mirrors><!-- mirror| Specif…...
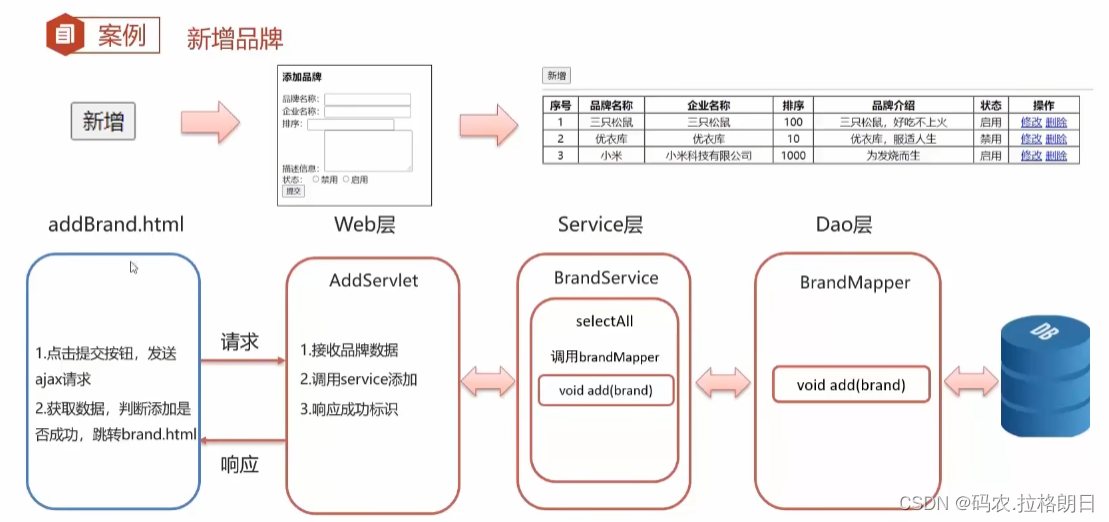
Ajax和Json综合案例
1. 查询所有 创建brand.html,使用axios发送请求,其中查询一般采用get的请求方式 <script src"js/axios-0.18.0.js"></script><script>//1. 当页面加载完成后,发送ajax请求window.onload function () {//2. 发送ajax请求axi…...

【genius_platform软件平台开发】第九十四讲:int64_t的格式化问题(lld和PRId64)
问题起因是在进行上位机软件优化的工作安排时,同事对unsigned long long 类型的时间戳进行了格式化输出优化,从%ull优化为了% PRIu64,我进行代码合并请求处理的时候突然感觉这个可以仔细查一下。查阅到的相关资料如下: * 1. int6…...

多模态之clip
论文:Learning Transferable Visual Models From Natural Language Supervision Github:https://github.com/OpenAI/CLIP OpenAI出品 论文通过网络爬取4亿(image, text)对,使用对比学习的方法训练得到clip(Contrastive Languag…...
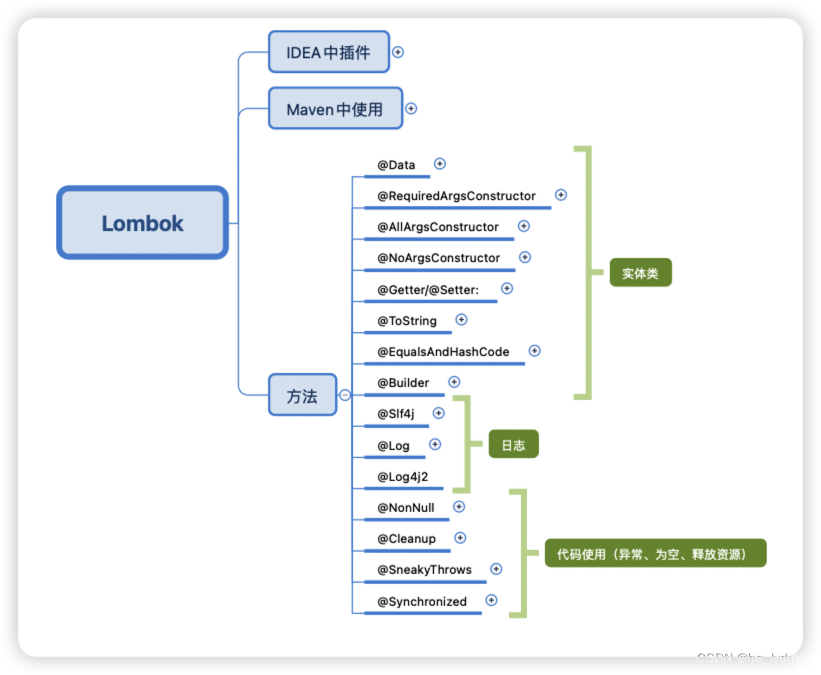
Lombok常用注解
文章目录 一、简介二、Idea中配置三、Maven中配置四、相应注解1、Data2、RequiredArgsConstructor3、AllArgsConstructor4、NoArgsConstructor5、Getter/Setter:6、ToString7、EqualsAndHashCode8、Builder9、NonNull10、Log11、Slf4j12、Log4j213、SneakyThrows14、Cleanup15、…...

加拿大各省接受公立教育的初始年龄汇总 — 供携子女赴加的访学、博后参考
近年来到加拿大从事访问学者和博士后研究的申请者日益增多,有些申请者想带孩子同去上公立学校。因为加拿大各省教育局政策有差异,所以入学(包括学前班)年龄不同,为此知识人网小编整理本文为大家解惑答疑。 加拿大为本国…...

数字化工厂:虹科Vuzix AR眼镜在工业制造中的革新应用
随着现代科学技术和新兴需求的快速增长,增强现实(AR)、各种“现实”产品与技术不断涌入创新市场,新兴用例数量正在快速增长,可以肯定,在可预见的未来,AR技术将成为各行各业的生产与工作主流。 增强现实(AR&…...
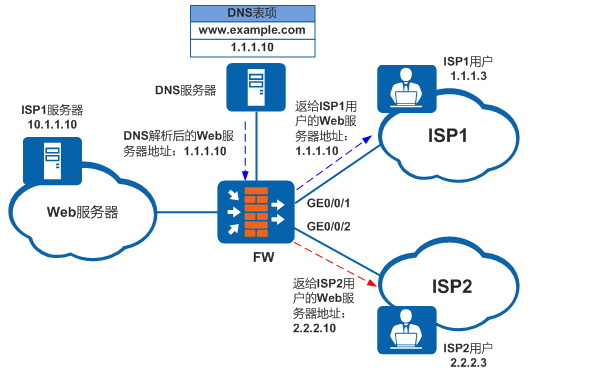
配置出接口方式的单服务器智能DNS
组网需求 如图1所示,企业部署了一台ISP1服务器对外提供Web服务,域名为www.example.com。ISP1服务器的私网IP地址为10.1.1.10,服务器映射后的公网IP地址为1.1.1.10。企业的DNS服务器上存在域名www.example.com与ISP1服务器地址1.1.1.10的对应关…...

数据结构初阶(栈和队列)
文章目录 一、栈1.1 什么是栈1.2 栈的使用(1)底层代码(2)方法(3)栈的应用 二、队列2.1 什么是队列2.2 队列的使用(1)底层代码的实现(2)队列的使用 2.3 双端队…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...
