基于KZG多项式承诺方案的RLN
1. 引言
RLN——Rate-Limiting Nullifier为PSE团队主导的项目,源自:
- Barry White Hat 2019年博客 Semaphore RLN, rate limiting nullifier for spam prevention in anonymous p2p setting
RLN(Rate-Limiting Nullifier)是一种zk小工具/协议,可为匿名环境启用垃圾邮件预防机制。旨在:
- 在每个epoch使用KZG多项式承诺
- 为每个message使用KZG opening
- 为单个message生成proof的时间应小于1ms,几乎改进约1000倍
- 使用RLN作为垃圾邮件保护层(spam protection layer),从而具有网络层面的隐私,可用于Tor网络和以太坊validator网路
从技术层面上来说,transmitter选中某多项式 f ( X ) f(X) f(X),其中 f ( 0 ) f(0) f(0)为其想要保护的私钥,当发送某message时,实际发送的是该多项式上的某个点。
若 f ( X ) f(X) f(X)为 n n n阶多相似,则所发送的message数量上限为 n n n,transmitter若发送多于 n n n个不同的message,则其私钥将会泄露。
实际使用zkSNARK来:
- 使用membership proof,来确保transmitter对某proof of stake进行了承诺
- 使用message proof,来证明其包含了多项式上的某个点。
当前的问题在于,为单个message来生成proof需约1s,在很多场景下并不实用——如Tor网路、Validator网络、手机环境等。需要利用KZG多项式承诺和KZG opening方案,将单个message证明时间由1s提高到1ms。
具体场景为:
- 某指定epoch e e e和message数量上限(message limit) n n n,用户创建某degree为 n n n的多项式,满足 f ( 0 ) f(0) f(0)为该用户的私钥 p k pk pk。
- 可信设置(trusted setup):
- 对于message数量上限为 n n n的场景,需要shared common reference: g , g α , g α 2 , ⋯ , g α n g,g^{\alpha}, g^{\alpha^2},\cdots,g^{\alpha^n} g,gα,gα2,⋯,gαn
- 对于非匿名版本:需为每个message limit执行可信设置。
- 对于匿名版本:可使用现有的reference。
- 对于message数量上限为 n n n的场景,需要shared common reference: g , g α , g α 2 , ⋯ , g α n g,g^{\alpha}, g^{\alpha^2},\cdots,g^{\alpha^n} g,gα,gα2,⋯,gαn
承诺是指:
- 用户为某epoch选中某 n n n-degree多项式,最多可发送 n n n个message,其中 f ( 0 ) f(0) f(0)为用户私钥 p k pk pk。
- 使用reference string用户计算KZG多项式承诺 C = g f ( α ) C=g^{f(\alpha)} C=gf(α)。
- 在特定epcoh,用户分享该多项式承诺 C C C。
- 为发送某message,用户分享 ( f ( m ) , g ψ m ( α ) ) (f(m), g^{\psi_m(\alpha)}) (f(m),gψm(α)),其中 m m m为message的哈希值, g ψ m ( α ) g^{\psi_m(\alpha)} gψm(α)为相应的opening proof,其中 ψ m ( x ) = f ( x ) − f ( m ) x − m \psi_m(x)=\frac{f(x)-f(m)}{x-m} ψm(x)=x−mf(x)−f(m)。
对某message的evaluation为:
- 计算message的哈希值: m m m
- RLN message为: m , f ( m ) , g ψ m ( α ) m,f(m),g^{\psi_m(\alpha)} m,f(m),gψm(α)
- Verifier具有该epoch的多项式承诺值 g f ( α ) g^{f(\alpha)} gf(α)
- Verifier对message进行evaluate:
e ( g f ( α ) , g ) = ? e ( g ψ m ( α ) , g α ⋅ g − m ) ⋅ e ( g , g ) f ( m ) e(g^{f(\alpha)},g)\overset{\text{?}}{=}e(g^{\psi_m(\alpha)},g^{\alpha}\cdot g^{-m})\cdot e(g,g)^{f(m)} e(gf(α),g)=?e(gψm(α),gα⋅g−m)⋅e(g,g)f(m)
为此,设计了3个版本:
- Version A:具体的原型设计见:
https://github.com/Rate-Limiting-Nullifier/kzg-rln/blob/main/versionA/src/main.rs(Rust) - Version B
- Version C
这3个版本的性能对比为:【可在epoch之初缓存 e ( g f ( α ) , g ) e(g^{f(\alpha)},g) e(gf(α),g)以供之后的message verification过程中使用,因此,每个message verification仅需2次pairing运算。】

2. Version A:非匿名的最简单方案
关键点为:
- 用户的公钥为: g f ( 0 ) g^{f(0)} gf(0)
- 用户提供多项式承诺值、用户公钥以及opening proof: g f ( α ) , g ψ 0 ( α ) , g f ( 0 ) g^{f(\alpha)},g^{\psi_0(\alpha)},g^{f(0)} gf(α),gψ0(α),gf(0)
- Verifier:通过验证KZG commitment的opening,检查用户公钥 g f ( 0 ) g^{f(0)} gf(0)在所承诺的多项式上。
e ( g ψ 0 ( α ) , g α ) ⋅ e ( g , g f ( 0 ) ) = ? e ( g , g f ( α ) ) e(g^{\psi_0(\alpha)},g^{\alpha})\cdot e(g,g^{f(0)})\overset{\text{?}}{=}e(g,g^{f(\alpha)}) e(gψ0(α),gα)⋅e(g,gf(0))=?e(g,gf(α))
3. Version B:借助ZKP实现的匿名方案
ZKP针对的场景为:
- public信息有: g f ( α ) , n g^{f(\alpha)},n gf(α),n
- private信息有: f ( x ) , p k f(x),pk f(x),pk
- 约束有:
- f ( 0 ) = p k f(0)=pk f(0)=pk
- membership proof of g f ( 0 ) g^{f(0)} gf(0)
- f ( x ) = ∑ i = 0 k c i x i f(x)=\sum_{i=0}^{k}c_ix^i f(x)=∑i=0kcixi,当 i > n i>n i>n时有 c i = 0 c_i=0 ci=0
用户提供proof π \pi π和多项式承诺值 g f ( α ) g^{f(\alpha)} gf(α)。
Verifier检查proof:
verify ( π , g f ( α ) , root , n ) → t r u e \text{verify}(\pi, g^{f(\alpha)},\text{root},n)\to true verify(π,gf(α),root,n)→true
4. Version C:为多个epoch承诺 使用multiple多项式承诺 的匿名方案
multiple多项式承诺方案为:
- 用户为 m m m个epoch创建 m m m个degree为 n n n的多项式,然后对这些多项式同时承诺。
- 对于某epoch,对应的 n n n-degree多项式为 f e ( x ) f_e(x) fe(x),将其表示为 f e ( x ) = ∑ i = 0 n c i ( e ) ⋅ x i f_e(x)=\sum_{i=0}^{n}c_i(e)\cdot x^i fe(x)=∑i=0nci(e)⋅xi,从而有:
f 1 ( x ) = c 0 ( 1 ) + c 1 ( 1 ) x + c 2 ( 1 ) x 2 + ⋯ + c n ( 1 ) x n f_1(x)=c_0(1)+c_1(1)x+c_2(1)x^2+\cdots+c_n(1)x^n f1(x)=c0(1)+c1(1)x+c2(1)x2+⋯+cn(1)xn
f 2 ( x ) = c 0 ( 2 ) + c 1 ( 2 ) x + c 2 ( 2 ) x 2 + ⋯ + c n ( 2 ) x n f_2(x)=c_0(2)+c_1(2)x+c_2(2)x^2+\cdots+c_n(2)x^n f2(x)=c0(2)+c1(2)x+c2(2)x2+⋯+cn(2)xn
f 3 ( x ) = c 0 ( 3 ) + c 1 ( 3 ) x + c 2 ( 3 ) x 2 + ⋯ + c n ( 3 ) x n f_3(x)=c_0(3)+c_1(3)x+c_2(3)x^2+\cdots+c_n(3)x^n f3(x)=c0(3)+c1(3)x+c2(3)x2+⋯+cn(3)xn
⋮ \vdots ⋮
f m ( x ) = c 0 ( m ) + c 1 ( m ) x + c 2 ( m ) x 2 + ⋯ + c n ( m ) x n f_m(x)=c_0(m)+c_1(m)x+c_2(m)x^2+\cdots+c_n(m)x^n fm(x)=c0(m)+c1(m)x+c2(m)x2+⋯+cn(m)xn - 用户为每个 c i ( e ) c_i(e) ci(e)创建多项式承诺
对应ZKP针对的场景为:
- public信息有: g c i ( α ) , n , m g^{c_i(\alpha)},n,m gci(α),n,m
- private信息有: c i ( e ) , p k c_i(e),pk ci(e),pk
- 约束有:
- 对于每个 e ≤ m e\leq m e≤m,有 c 0 ( e ) = p k c_0(e)=pk c0(e)=pk
- f e ( x ) = ∑ i = 0 k c i ( e ) x i f_e(x)=\sum_{i=0}^{k}c_i(e)x^i fe(x)=∑i=0kci(e)xi,当 i > n i>n i>n,有 c i ( e ) = 0 c_i(e)=0 ci(e)=0
- membership proof of g f e ( 0 ) g^{f_e(0)} gfe(0)
- 多项式承诺值 g c i ( α ) g^{c_i(\alpha)} gci(α)是正确的
验证过程为:
- 对于注册阶段:
- Verifier检查proot:
verify ( π , g c 0 ( α ) , ⋯ , g c n ( α ) , root , n , m ) → t r u e \text{verify}(\pi, g^{c_0(\alpha)},\cdots,g^{c_n(\alpha)},\text{root},n,m)\to true verify(π,gc0(α),⋯,gcn(α),root,n,m)→true
- Verifier检查proot:
- 对于每个epoch e e e:
- 用户提交:
-
{ ( g c 0 ( e ) , g ϕ 0 , e ( α ) ) , ( g c 1 ( e ) , g ϕ 1 , e ( α ) ) , ⋯ , ( g c n ( e ) , g ϕ n , e ( α ) ) } \{(g^{c_0(e)},g^{\phi_{0,e}(\alpha)}),(g^{c_1(e)},g^{\phi_{1,e}(\alpha)}),\cdots,(g^{c_n(e)},g^{\phi_{n,e}(\alpha)})\} {(gc0(e),gϕ0,e(α)),(gc1(e),gϕ1,e(α)),⋯,(gcn(e),gϕn,e(α))},其中 ϕ ( i , e ) ( x ) = c i ( x ) − c i ( e ) x − e \phi_{(i,e)}(x)=\frac{c_i(x)-c_i(e)}{x-e} ϕ(i,e)(x)=x−eci(x)−ci(e)
-
为检查 g f e ( α ) = ∏ i = 0 n g c i ( e ) α i g^{f_e(\alpha)}=\prod_{i=0}^{n}g^{c_i(e)\alpha^i} gfe(α)=∏i=0ngci(e)αi,Verifier检查:
e ( g , g f e ( α ) ) = e ( g , ∏ i = 0 n g c i ( e ) α i ) = ? ∏ i = 0 n e ( g c i ( e ) , g α i ) e(g,g^{f_e(\alpha)})=e(g,\prod_{i=0}^{n}g^{c_i(e)\alpha^i})\overset{\text{?}}{=}\prod_{i=0}^{n}e(g^{c_i(e)},g^{\alpha^i}) e(g,gfe(α))=e(g,∏i=0ngci(e)αi)=?∏i=0ne(gci(e),gαi)- 对于 i = 0 , ⋯ , n i=0,\cdots,n i=0,⋯,n,借助同态属性,Verifier检查用户在多项式承诺值中隐藏的系数:
e ( g c i ( α ) , g ) = ? e ( g ϕ i , e ( α ) , g α ⋅ g − e ) ⋅ e ( g , g c i ( e ) ) e(g^{c_i(\alpha)},g)\overset{\text{?}}{=}e(g^{\phi_{i,e}(\alpha)},g^{\alpha}\cdot g^{-e})\cdot e(g,g^{c_i(e)}) e(gci(α),g)=?e(gϕi,e(α),gα⋅g−e)⋅e(g,gci(e))
其中 ϕ i , e ( x ) = c i ( x ) − c i ( e ) x − e \phi_{i,e}(x)=\frac{c_i(x)-c_i(e)}{x-e} ϕi,e(x)=x−eci(x)−ci(e)
- 对于 i = 0 , ⋯ , n i=0,\cdots,n i=0,⋯,n,借助同态属性,Verifier检查用户在多项式承诺值中隐藏的系数:
-
然后:
- 计算message的哈希值: m m m
- RLN message有: m , f ( m ) , g ψ m ( α ) m,f(m),g^{\psi_m(\alpha)} m,f(m),gψm(α)
- Verifier evaluate the message:
e ( g f ( α ) , g ) = ? e ( g ψ m ( α ) , g α ⋅ g − m ) ⋅ e ( g , g ) f ( m ) e(g^{f(\alpha)},g)\overset{\text{?}}{=}e(g^{\psi_m(\alpha)},g^{\alpha}\cdot g^{-m})\cdot e(g,g)^{f(m)} e(gf(α),g)=?e(gψm(α),gα⋅g−m)⋅e(g,g)f(m)
-
- 用户提交:
参考资料
[1] 2023年4月 ethresearch和zkresearch联合发布 RLN on KZG polynomial commitment scheme [cross-posted]
相关文章:

基于KZG多项式承诺方案的RLN
1. 引言 RLN——Rate-Limiting Nullifier为PSE团队主导的项目,源自: Barry White Hat 2019年博客 Semaphore RLN, rate limiting nullifier for spam prevention in anonymous p2p setting RLN(Rate-Limiting Nullifier)是一种…...
《站在巨人的肩膀上学习Java》
Java从诞生距今已经有28年了,在这段时间里,随着Java版本的不断迭代,Java新特性的不断出现,使得Java被使用的越来越广泛。在工程界Java语言一直是大家最喜欢的语言之一,Java一直排行在编程语言热门程度的前3名。 可想而…...
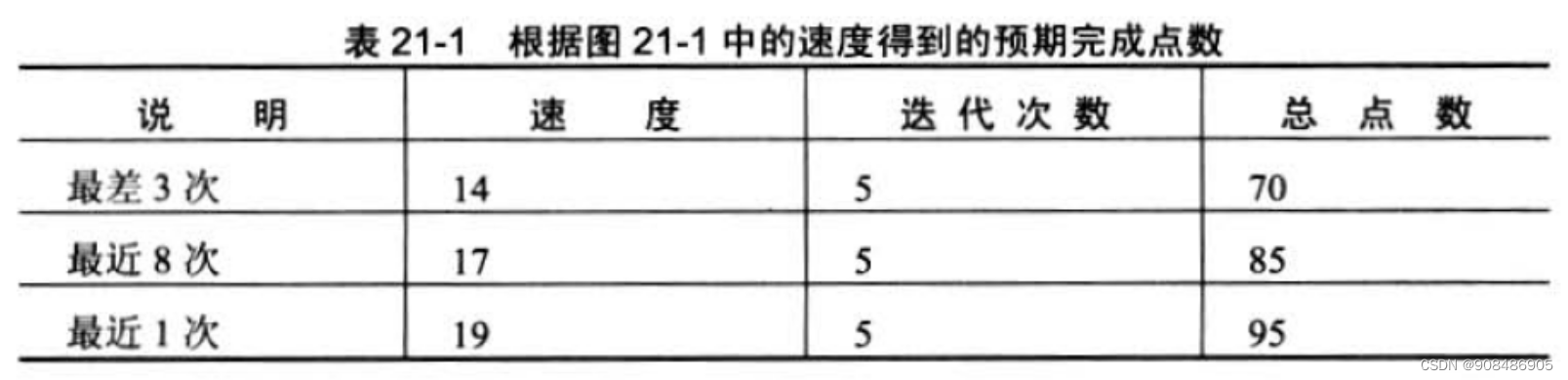
敏捷ACP.敏捷估计与规划.Mike Cohn.
第一部分 传统规划失败的原因 vs 敏捷规划有效的原因 传统的项目规划方式往往会让我们失望。要回答-一个 新产品的范围/进度/资源的组合问题,传统规划过程不一定会产生令人非常满意的答案和最终产品。以下- -些论据可以支持这个结论: ●大约2/3的项目会显著超…...
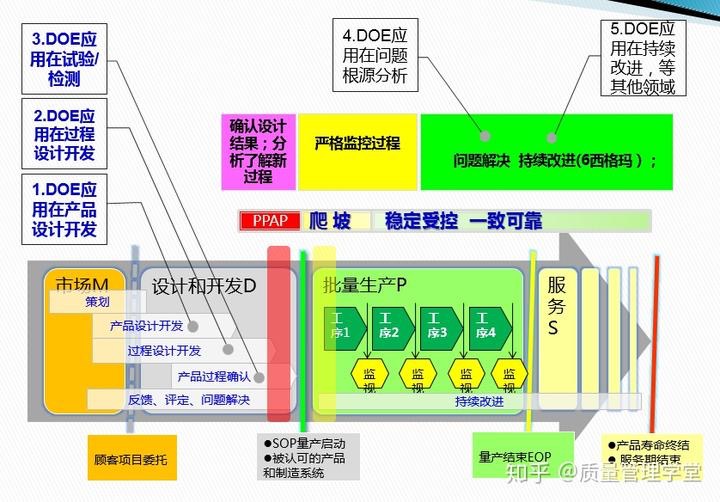
[创新工具和方法论]-01- DOE课程基础知识
文章目录 1.DOE实验设计的介绍1.1 什么是实验设计DOE?1.2 DOE的优势有哪些?1.3 如何开展DoE研究?步骤 2.DOE实验培训3.数据分析步骤4.实验的随机化5.偏差6.R方 相关系数假设检验 7.三因子二水平全因子设计 1.DOE实验设计的介绍 实验设计是一种安排实验和分析实验数…...
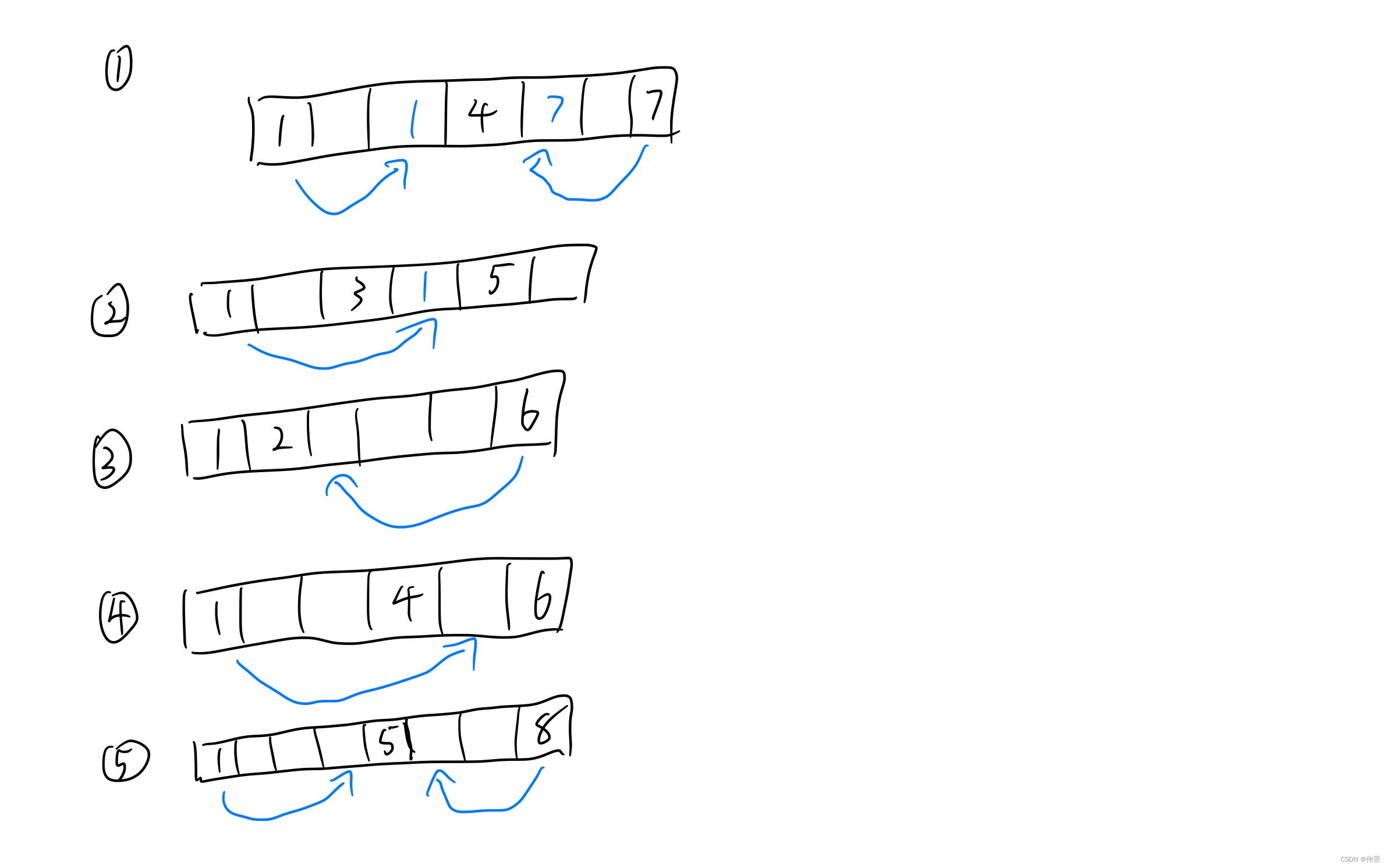
LeetCode-1033. 移动石子直到连续
题目链接 LeetCode-1033. 移动石子直到连续 题目描述 题解 题解一(Java) 作者:仲景 这题目挺难懂的,得画画图才能更好的理解 这也是LeetCode的尿性,习惯了,非得整这种别人看不懂的鸟语 你可以这样理解&a…...

JVM调优入门指南:掌握步骤、参数和场景
前言 作为Java开发者,我们经常需要优化应用的性能,其中JVM调优是非常重要的一部分。在本文中,我们将介绍JVM调优的一般步骤和方法,了解JVM调优参数,如堆大小、新生代比例、GC算法等参数的作用和配置方式,并…...

基于JSP+MySQL的跳蚤市场网站设计与开发
摘 要 在当今社会,网络信息已经不是什么很陌生的词汇,每天都在这个信息时代里生活着并且享受着它带来的与众不同。网络购物可以说是飞速发展的,这种购物方式逐渐的影响着人们的衣食住行。所以利用计算机实现 跳蚤市场网站设计与开发势在必行。本网站是一个校园的跳蚤市场网…...
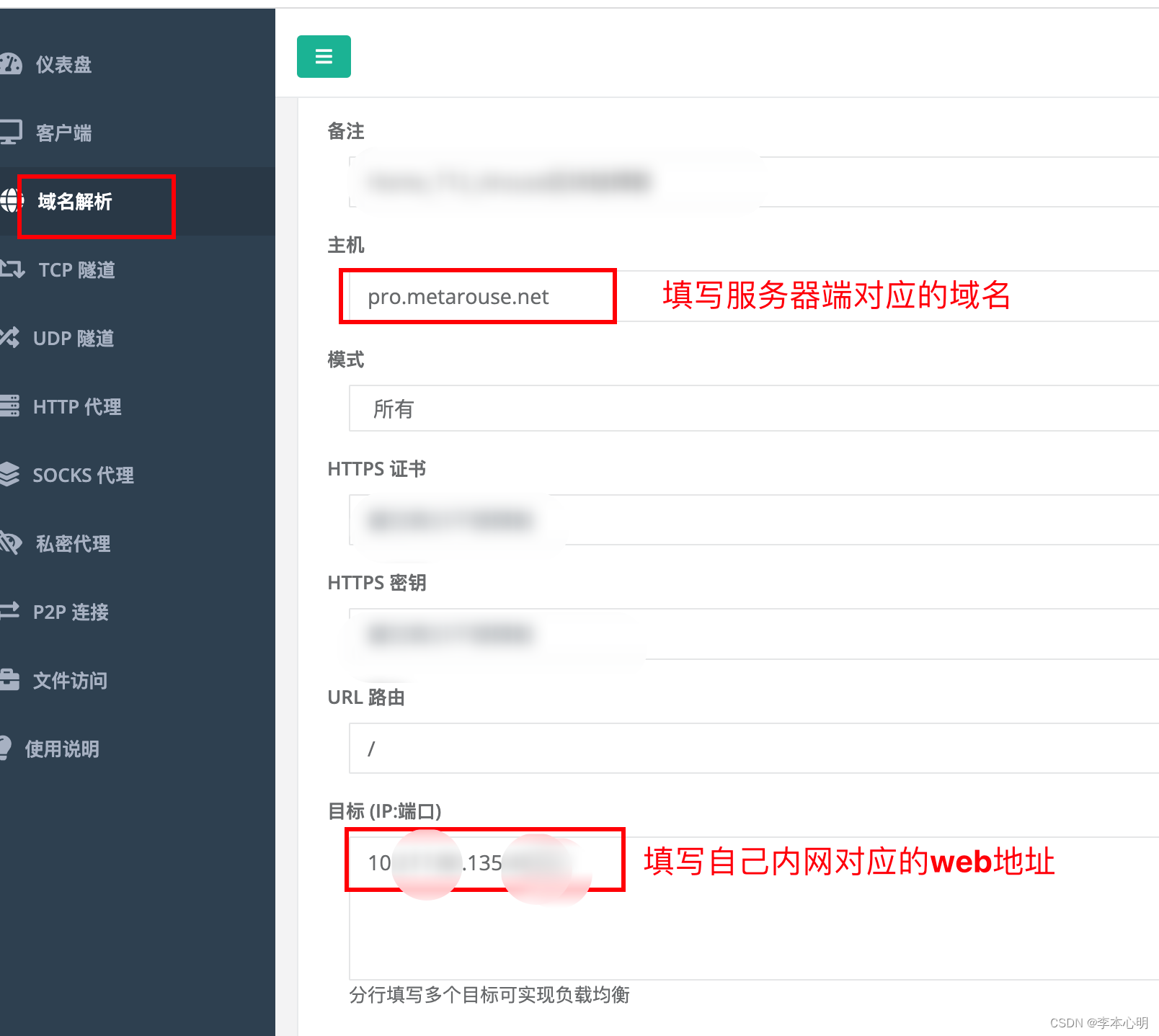
内网穿透NPS和宝塔Nginx配合使用,开启SSL访问本地局域网网络
并非为了教学,仅供自己记录,方便下次用。所以内容不会刻意花时间写的很细节详细。 1. 服务器NPS配置 NPS install安装后,配置文件会在其他位置,通过是 /etc/nps/nps.conf目录。 找到进行修改,主要修改的是http_proxy_p…...

ToLua框架
ToLua 是一个用于在 Unity 中为 Lua 提供 C# 语言绑定的框架。通过 ToLua,你可以方便地将 C# 代码暴露给 Lua 脚本,并在 Lua 脚本中调用 C# 类、方法和属性。 更新流程 原理:使用AssetBundle进行资源的更新,而由于lua运行时才编…...
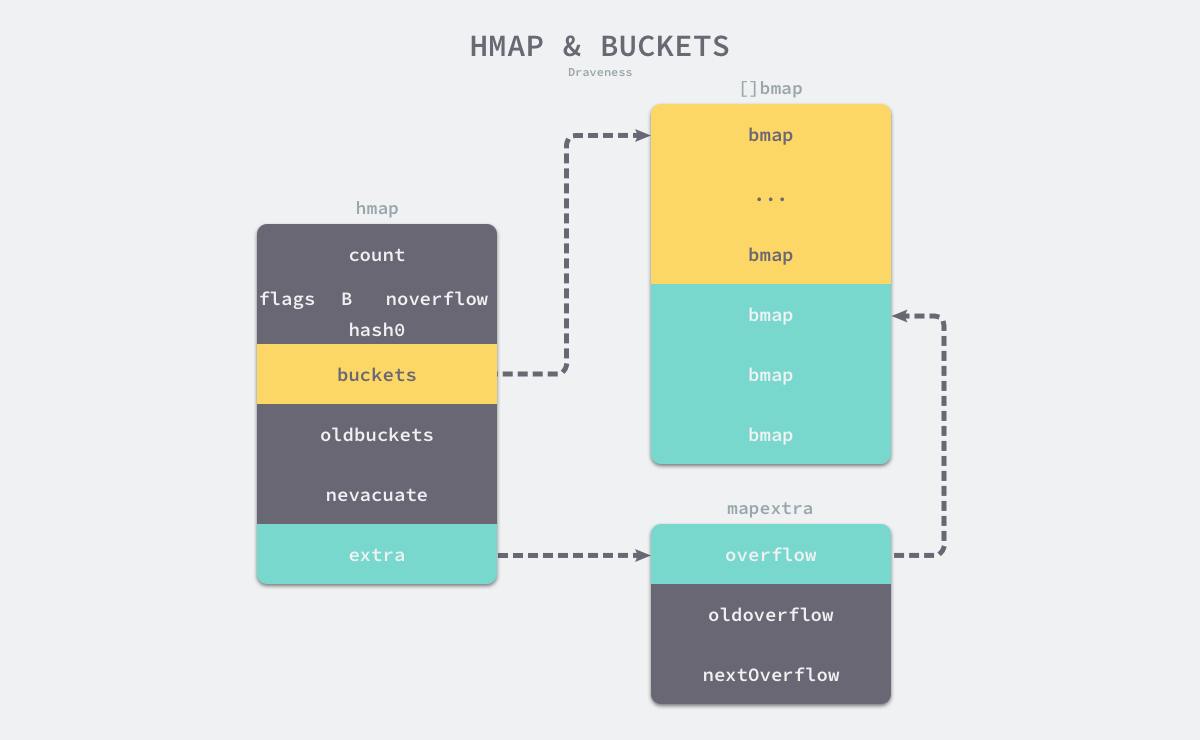
Golang-常见数据结构Map
Map map 是一种特殊的数据结构:一种元素对(pair)的无序集合,pair 的一个元素是 key,对应的另一个元素是 value,所以这个结构也称为关联数组或字典。这是一种快速寻找值的理想结构:给定 key&…...
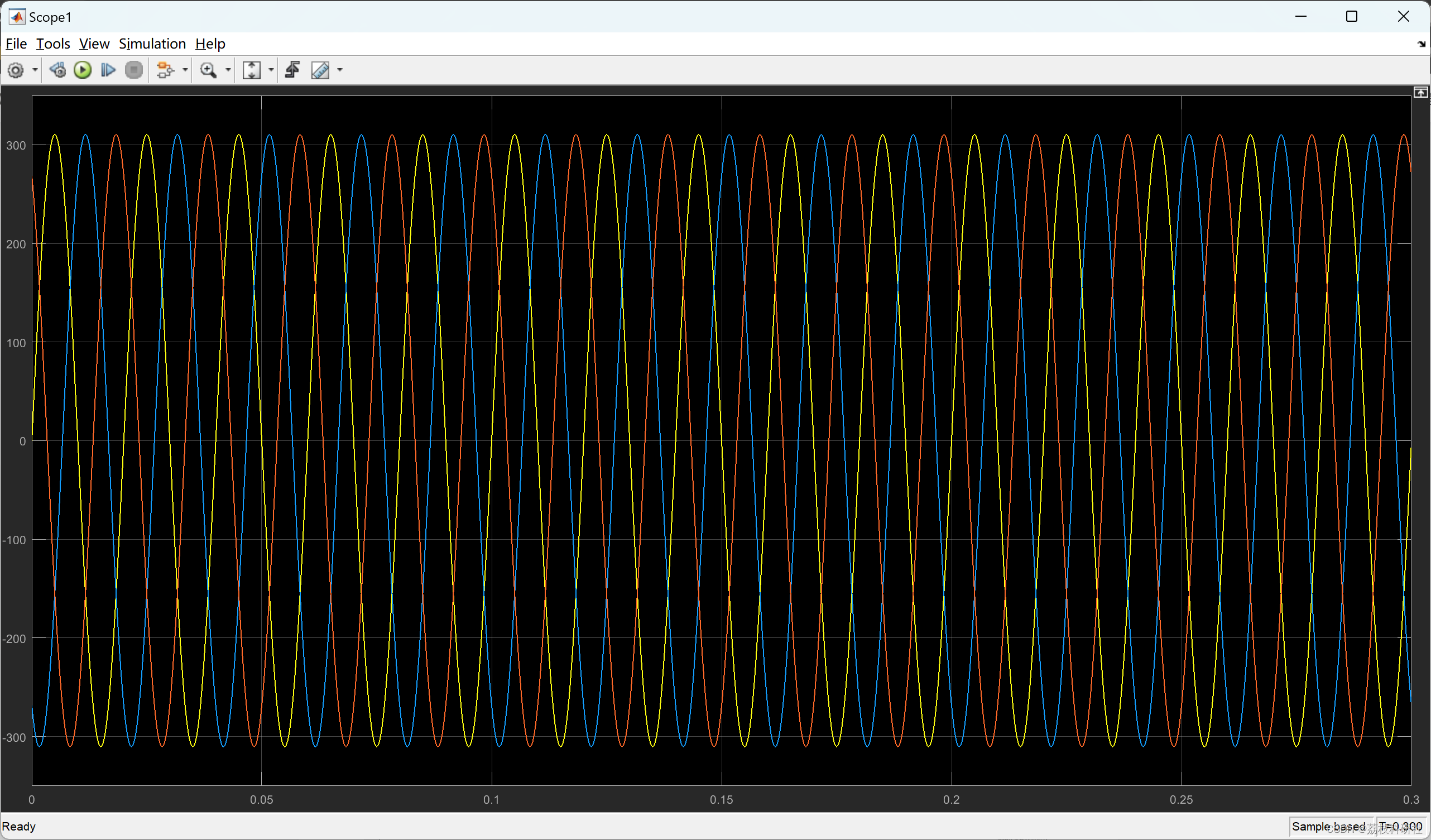
基于空间矢量脉宽调制(SVPWM)的并网逆变器研究(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

介绍tcpdump在centos中的使用方法
tcpdump是一款强大的命令行数据包分析器,支持多种过滤和抓包参数。下面将介绍tcpdump的常用抓包参数。当需要监控CentOS系统的网络流量或者进行网络故障排查时,可以使用tcpdump来捕获数据包并进行分析。 下面介绍在CentOS中使用tcpdump的方法࿱…...
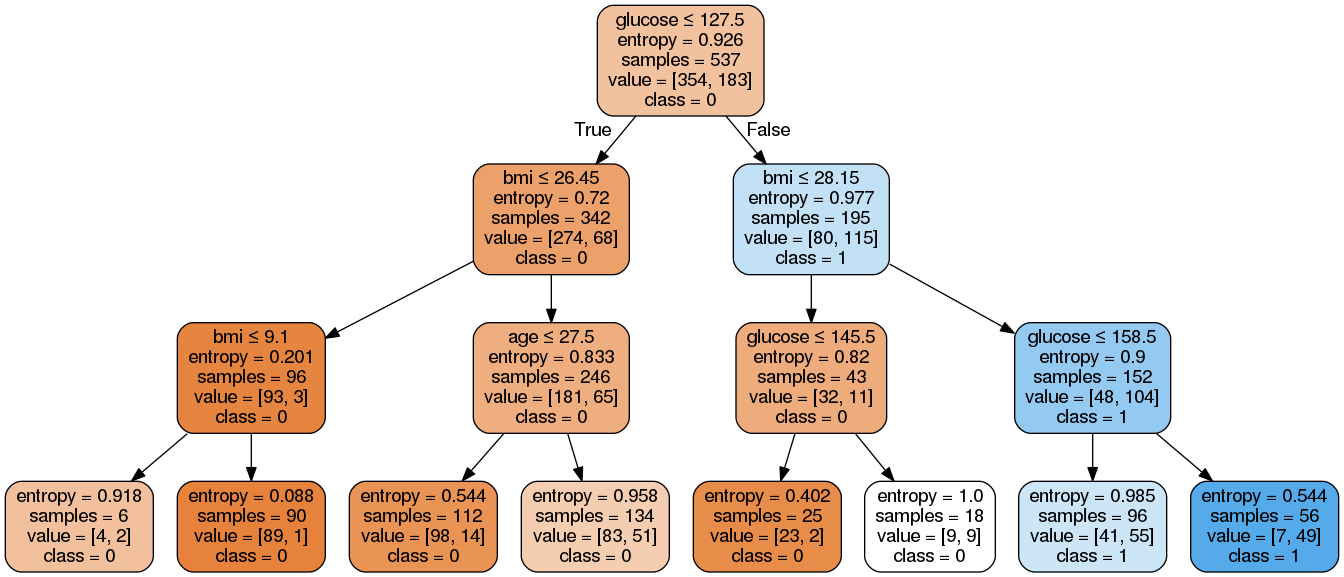
机器学习实战:Python基于DT决策树模型进行分类预测(六)
文章目录 1 前言1.1 决策树的介绍1.2 决策树的应用 2 Scikit-learn数据集演示2.1 导入函数2.2 导入数据2.3 建模2.4 评估模型2.5 可视化决策树2.6 优化模型2.7 可视化优化模型 3 讨论 1 前言 1.1 决策树的介绍 决策树(Decision Tree,DT)是一…...
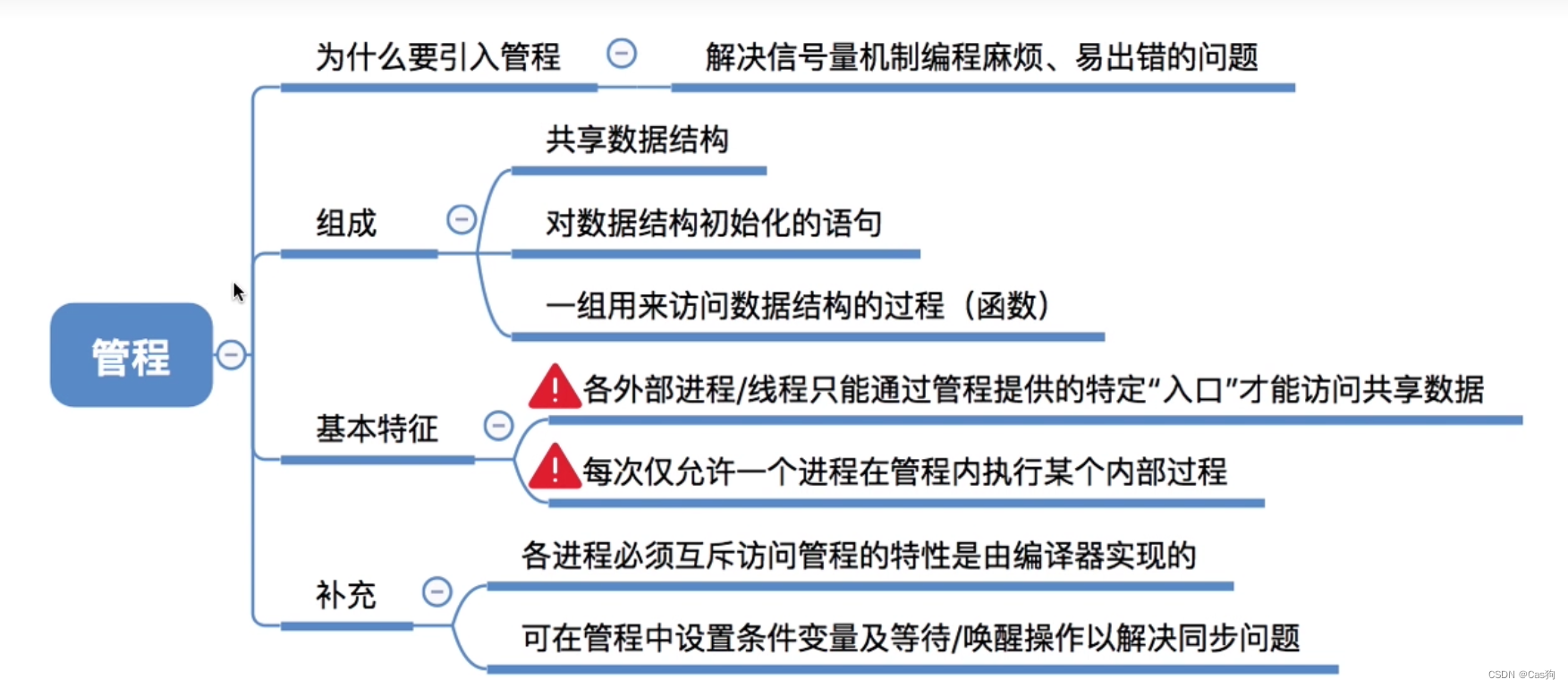
操作系统之进程同异步、互斥
引入 异步性是指,各并发执行的进程以各自独立的、不可预知的速度向前推进。 但是在一定的条件之下,需要进程按照一定的顺序去执行相关进程: 举例说明1: 举例说明2: 读进程和写进程并发地运行,由于并发必然导致异步性…...

你了解这2类神经性皮炎吗?常常预示着这5类疾病!
神经性皮炎属于慢性皮肤病,患者皮肤可出现局限性苔藓样变,同时伴有阵发性瘙痒。神经性皮炎易发生在颈部两侧和四肢伸侧,中年人是高发人群。到目前为止神经性皮炎病因还并不是很明确,不过一部分病人发病前常常出现精神神经方面异常…...
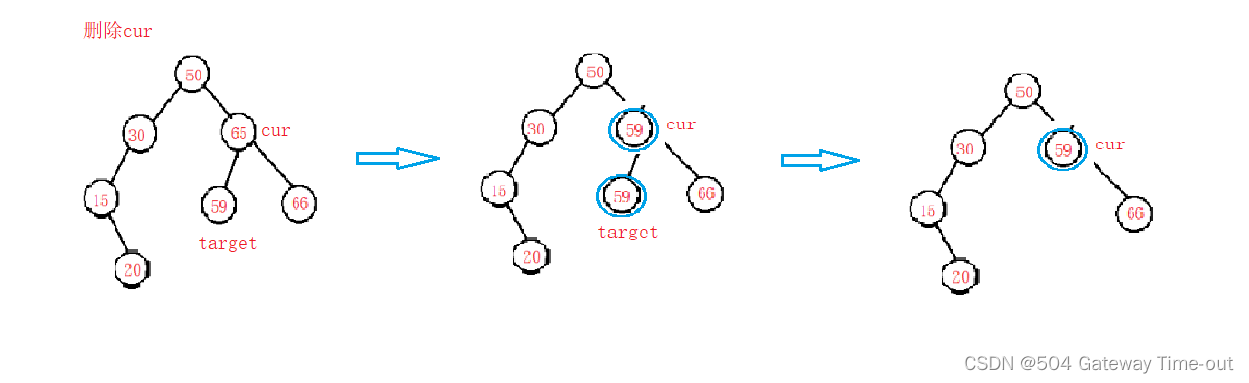
二叉搜索树【Java】
文章目录 二叉搜索树的性质二叉搜索树的操作遍历查找插入删除 二叉搜索树又称为二叉排序树,是一种具有一定性质的特殊的二叉树; 二叉搜索树的性质 若它的左子树不为空,则左子树上结点的值均小于根节点的值; 若它的右子树不为空&a…...

二叉树的遍历方式
文章目录 层序遍历——队列实现分析Java完整代码 先序遍历——中左右分析递归实现非递归实现——栈实现 中序遍历——左中右递归实现非递归实现——栈实现 后续遍历——左右中递归实现非递归实现——栈加标志指针实现 总结 层序遍历——队列实现 给你二叉树的根节点 root &…...
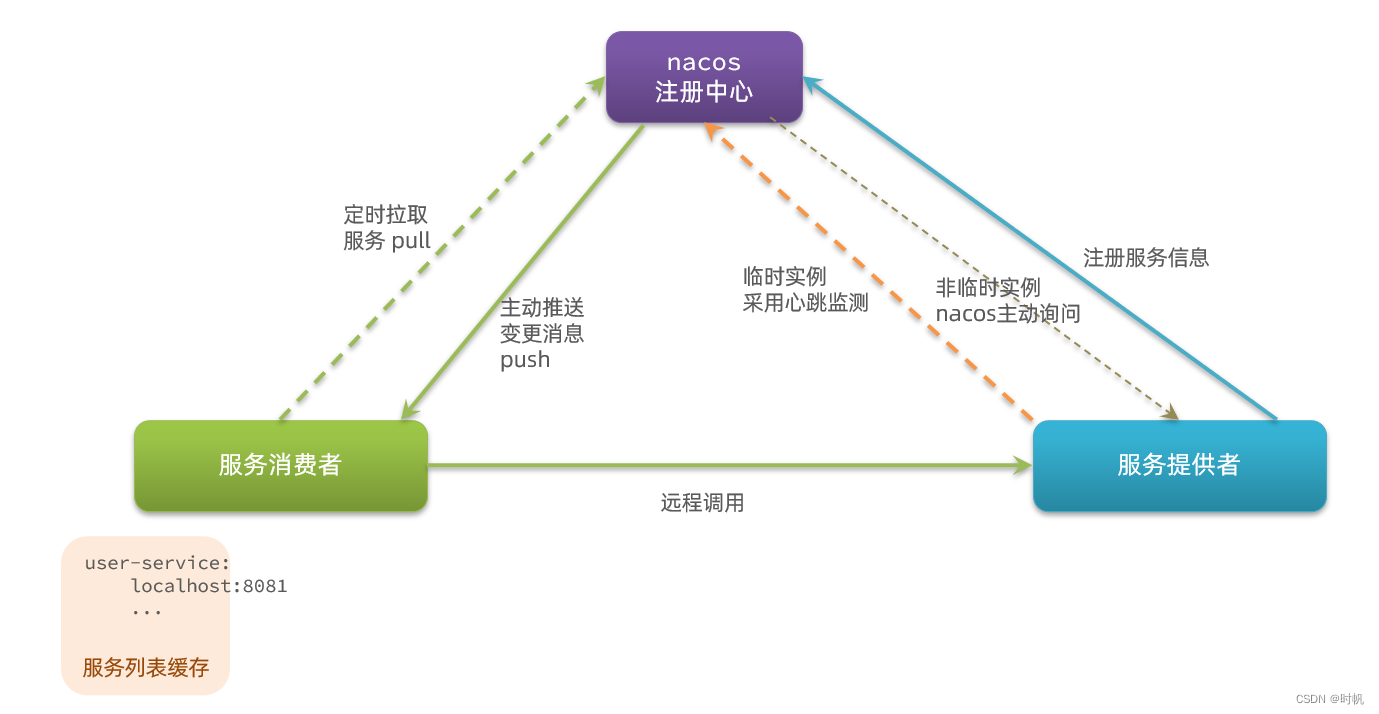
SpringCloud01
SpringCloud01 微服务入门案例 实现步骤 导入数据 实现远程调用 MapperScan("cn.itcast.order.mapper") SpringBootApplication public class OrderApplication {public static void main(String[] args) {SpringApplication.run(OrderApplication.class, args);}…...

SpringBoot整合Redis实现点赞、收藏功能
前言 点赞、收藏功能作为常见的社交功能,是众多Web应用中必不可少的功能之一。而redis作为一个基于内存的高性能key-value存储数据库,可以用来实现这些功能。 本文将介绍如何使用spring boot整合redis实现点赞、收藏功能,并提供前后端页面的…...

【Java入门合集】第一章Java概述
【Java入门合集】第一章Java概述 博主:命运之光 专栏:JAVA入门 学习目标 1.理解JVM、JRE、JDK的概念; 2.掌握Java开发环境的搭建,环境变量的配置; 3.掌握Java程序的编写、编译和运行; 4.学会编写第一个Java程序&#x…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
