P1050 [NOIP2005 普及组] 循环
题目描述
乐乐是一个聪明而又勤奋好学的孩子。他总喜欢探求事物的规律。一天,他突然对数的正整数次幂产生了兴趣。
众所周知,22 的正整数次幂最后一位数总是不断的在重复 2,4,8,6,2,4,8,6…2,4,8,6,2,4,8,6… 我们说 22 的正整数次幂最后一位的循环长度是 44(实际上 44 的倍数都可以说是循环长度,但我们只考虑最小的循环长度)。类似的,其余的数字的正整数次幂最后一位数也有类似的循环现象:
数字循环循环长度22,4,8,6433,9,7,1444,6255166177,9,3,1488,4,2,6499,12数字23456789循环2,4,8,63,9,7,14,6567,9,3,18,4,2,69,1循环长度44211442
这时乐乐的问题就出来了:是不是只有最后一位才有这样的循环呢?对于一个整数 �n 的正整数次幂来说,它的后k位是否会发生循环?如果循环的话,循环长度是多少呢?
注意:
- 如果 �n 的某个正整数次幂的位数不足 �k,那么不足的高位看做是 00。
- 如果循环长度是 �L,那么说明对于任意的正整数 �a,�n 的 �a 次幂和 �+�a+L 次幂的最后 �k 位都相同。
输入格式
共一行,包含 22 个整数 �n 和 �k。�n 和 �k 之间用一个空格隔开,表示要求 �n 的正整数次幂的最后 �k 位的循环长度。
输出格式
一个整数,表示循环长度。如果循环不存在,输出 −1−1。
输入输出样例
输入 #1复制
32 2
输出 #1复制
4
说明/提示
【数据范围】
对于 30%30% 的数据,满足 �≤4k≤4;
对于100%100% 的数据,满足 1≤�<101001≤n<10100,1≤�≤1001≤k≤100。
【题目来源】
NOIP 2005 普及组第四题
题意
给定两整数 �,�n,k,求 �n 的正整数次幂的最后 �k 位的循环长度,若循环不存在输出 −1−1。
1≤�≤10100,1≤�≤1001≤n≤10100,1≤k≤100
题解
这篇题解是对最高赞题解的补充与说明
在看最高赞题解的时候,因为没有放上计算过程,我对着题解手玩了好久才弄明白,所以就有了这篇附上计算过程的题解。
手玩数据 198123 4,因为要求只取后 4 位,所以将其截取成 8123。
我们逐位进行处理:
- 先处理最后一位的循环节:最后一位是
3,循环节长度为 4。所以后两位的循环节长度一定为 4 的倍数,为了加快计算,我们可以将乘数变为8123^4,取后 4 位变成0641。 - 再处理后两位:后两位是
23,在乘了 5 次0641后出现了循环,循环节长度为 4*5=20。同样为了加快计算,乘数变为8123^20=0641^5,取后 4 位变成9201。之后就按照这样的方法处理即可。 - 后三位:后三位是
123,乘了 5 次9201后出现循环,循环节长度为 20*5=100 ,乘数变为9201^5%(10^4)=6001 - 后四位:后四位是
8123,乘了 5 次6001后出现循环,循环节长度为 100*5=500,500 就是最终的答案。
记得判断无解的情况:如果在处理某一位时,乘了乘数 10 次,还是没有出现循环,无解。
8123 1
8123*8123=65983129 2
3129*8123=25416867 3
6867*8123=55780641 4
0641*8123=05206843 #
8123^4=43537733126306418123 1
8123*0641=05206843 2
6843*0641=04386363 3
6363*0641=04078683 4
8683*0641=05565803 5
5803*0641=03719723 #
0641^5=1082156687392018123 1
8123*9201=74739723 2
9723*9201=89461323 3
1323*9201=12172923 4
2923*9201=26894523 5
4523*9201=41616123 #
9201^5=659439797557264460018123 1
8123*6001=48746123 2
6123*6001=36744123 3
4123*6001=24742123 4
2123*6001=12740123 5
0123*6001=00738123 #ans=4*5*5*5=500
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int k;
char str[205];
struct bignum
{int x[205];bignum(){memset(x,0,sizeof(x));}
}n,tmp,mul,ans;
bignum operator *(bignum a,bignum b)//特化过的高精乘 只取后k位
{bignum ans;for(int i=0;i<k;i++)for(int j=0;j<k;j++)ans.x[i+j]+=a.x[i]*b.x[j];for(int i=0;i<k;i++)ans.x[i+1]+=ans.x[i]/10,ans.x[i]%=10;for(int i=k;i<205;i++)ans.x[i]=0;return ans;
}
bignum operator *(bignum a,int b)//这个高精乘低精是ans专用的233
{for(int i=0;i<=200;i++)a.x[i]*=b;for(int i=0;i<=200;i++)a.x[i+1]+=a.x[i]/10,a.x[i]%=10;return a;
}
int main()
{scanf("%s %d",str,&k);ans.x[0]=1;int len=strlen(str);for(int i=0;i<k;i++)n.x[i]=str[len-i-1]-'0';mul=n;for(int i=0;i<k;i++){bignum tmp=n;int j=1,flag=1;for(j=1;j<=10;j++){tmp=tmp*mul;if(tmp.x[i]==n.x[i]){ans=ans*j;flag=0;break;}}if(flag)return puts("-1"),0;tmp=mul;for(int k=1;k<j;k++)mul=mul*tmp;}len=200;while(ans.x[len]==0&&len>=1)len--;for(;len>=0;len--)putchar(ans.x[len]+'0');
}相关文章:

P1050 [NOIP2005 普及组] 循环
题目描述 乐乐是一个聪明而又勤奋好学的孩子。他总喜欢探求事物的规律。一天,他突然对数的正整数次幂产生了兴趣。 众所周知,22 的正整数次幂最后一位数总是不断的在重复 2,4,8,6,2,4,8,6…2,4,8,6,2,4,8,6… 我们说 22 的正整数次幂最后一位的循环长度…...
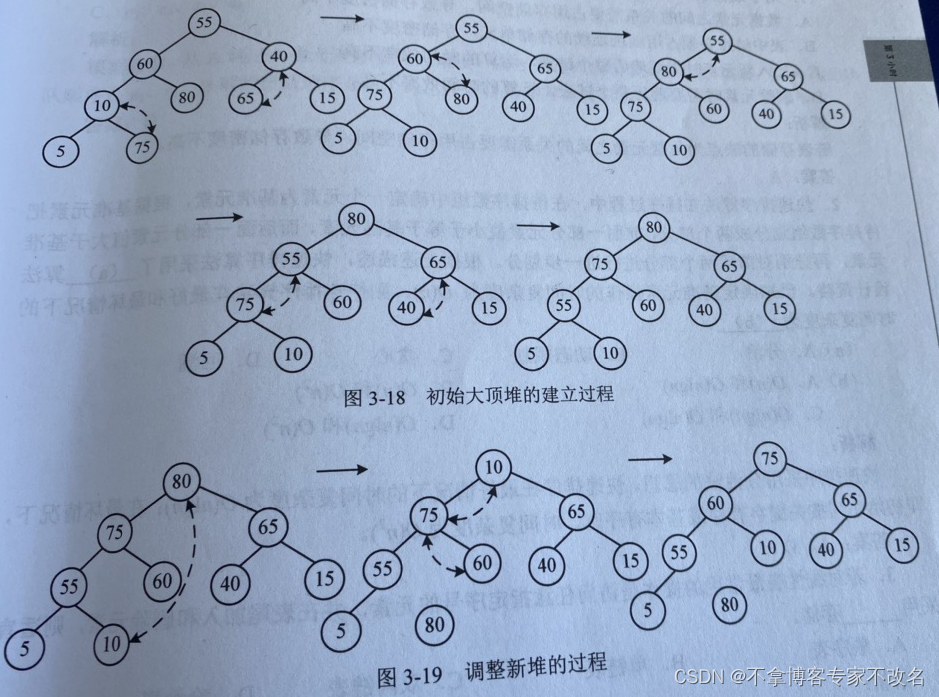
软考算法-排序篇-上
数据排序 一:故事背景二:直接插入排序2.1 概念2.2 画图表示2.3 代码实现2.4 总结提升 三:希尔排序3.1 概念3.2 画图表示3.3 代码实现3.4 总结提升 四:直接选择排序4.1 概念4.2 画图表示4.3 代码实现4.4 总结提升 五:堆…...

总结836
学习目标: 4月(复习完高数18讲内容,背诵21篇短文,熟词僻义300词基础词) 学习内容: 暴力英语:背诵《keep your direction》,默写,英语语法 高等数学:刷题&a…...

ginbuilder 工具快速创建
ginbuilder github 地址 快速创建一个ginweb项目: 目前apps下只有http服务,如果后续有需要的话,会添加上rpc服务,websocket服务后边如果有需要会添加上swagger 创建完成的目录结构 ├── apps │ ├── apis // 所有的apis…...

【Java基础面试宝典】堆、栈、方法区分别都存储了那些内容?wait 和 sleep 方法的区别?
目录 堆、栈、方法区分别都存储了那些内容? 堆(heap) 栈(stack) 方法区(method) 在 java 中 wait 和 sleep 方法的区别? 堆、栈、方法区分别都存储了那些内容? 堆&a…...

古剑飞仙手游Linux系统服务器架设教程
安装宝塔直接运行命令即可。 yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh 搭建环境: centos 7以上系统服务器 宝塔面板安装应用如下: Nginx1.14 mysql5.7 php5.6 1…...
(附python示例代码))
python实战应用讲解-【numpy数组篇】常用函数(十)(附python示例代码)
目录 Python Numpy MaskedArray.ravel()函数 Python Numpy MaskedArray.reshape()函数 Python Numpy MaskedArray.resize()函数 Python Numpy MaskedArray.std()函数 Python Numpy MaskedArray.sum()函数 Python Numpy MaskedArray.swapaxes()函数 Python Numpy MaskedA…...
练习题#2)
计算机组成原理(考研408)练习题#2
用于复习408或计算机组成原理期末考试。如有错误请在评论区指出。 So lets start studying with questions! それでは、問題の勉強を始めましょう! 11.某 cache 采用全相联映射,假设 cache 有 3 块,程序运行过程中需要访问的主存块号依 次为…...
Apache POI,springboot中导出excel报表
2. Apache POI 2.1 介绍 Apache POI 是一个处理Miscrosoft Office各种文件格式的开源项目。简单来说就是,我们可以使用 POI 在 Java 程序中对Miscrosoft Office各种文件进行读写操作。 一般情况下,POI 都是用于操作 Excel 文件。 Apache POI 的应用场景…...
-- 三种样式表)
CSS(一)-- 三种样式表
目录 1. 行内样式表 2. 内部样式表 3. 外部样式表(即引入 .css文件)(重点掌握) 1. 行内样式表 行内样式表(内联样式表)是在元素标签内部的 style 属性中设定 CSS 样式。适合于修改简单样式。 <di…...

嵌入式之Samba服务器搭建
在嵌入式系统开发应用平台中,tftp、nfs和samba服务器是最常用的文件传输工具 tftp和nfs是在嵌入式Linux开发环境中经常使用的传输工具 samba则是Linux和Windows之间的文件传输工具。 下面演示在linux上搭建Samba服务器 sudo apt-get install samba chmod -R 77…...
vue3+go——看到了就去学习吧
vue3go——看到了就去学习吧 Vue3.2 Vite Element-Plus 实现最基础的 CRUD1.效果展示【02:36】2.创建项目【03:16】3.添加github管理【04:10】4.引入element-plus【04:21】5.内容布局【08:59】6.布局优化【05:31】7.添加弹窗【09:34】8.ref改$ref【02:47】9.新增数据【09:22】…...

Perf工具统计CPU性能
Perf 性能检测工具 Perf 是一个内置于Linux内核中的工具,用于性能分析和调优。它可以对系统的CPU使用情况、内存使用情况、磁盘I/O、网络I/O等进行监控和分析,并提供了丰富的分析和可视化工具,以帮助用户定位和解决性能问题。perf可以进行函…...
考验大家指针功底的时候到了:请问如何理解 (int*)1 + 1 ?
来,猜猜看,这里的执行结果是什么? 这是今天课上的一道理解题,给大家一点点思考时间。 (心里有答案了再往下滑哦) 5 4 3 2 1 . 答案是,报warning!因为%d不是用来输出指针的哈…...

英语基础-介词
介词 方位介词 in:在…里面 Its in the box. 在盒子里 in my backpack 在背包里 in the tree 长在树上on:在…上面(指与物体表面接触) Its on the box. 在盒子上(和盒子接触) on the floor.在地板上 on the tree.在树上under:在…下面 Its unde…...
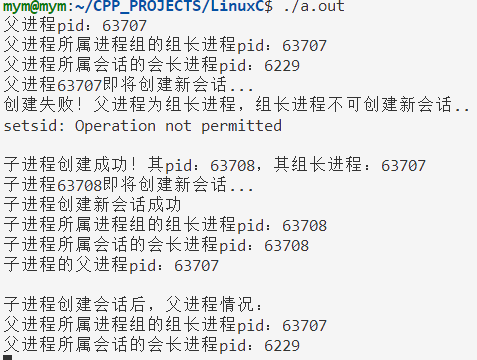
Linux进程通信:进程组 会话
1. 进程组 (1)概念:一个或多个进程的集合,也称为“作业”。 (2)父进程创建子进程时,默认属于同一个进程组。进程组ID为组长进程ID。 (3)进程组中只要有一个进程存在&a…...

【前端面经】JS-深浅拷贝
理解深浅拷贝 深浅拷贝问题的出现是由于JavaScript对不同类型的存储方式而引发的。 对于原始数据类型,它们的值是直接存储在栈内存中; 而复杂数据类型,则在栈内存中记录它的指针,而指针指向堆内存中真正的值。 所以对于原始数据类…...

【自然语言处理】实验2布置:Word2Vec TransE案例
NLP_class 学堂在线《自然语言处理》实验课代码报告,授课老师为刘知远老师。课程链接:https://www.xuetangx.com/training/NLP080910033761/1017121?channeli.area.manual_search。 持续更新中。 所有代码为作者所写,并非最后的“标准答案…...
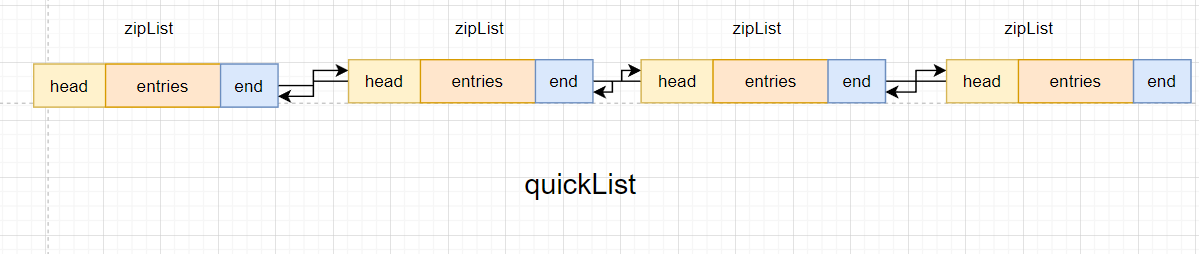
Redis集合底层实现原理
目录 本章重点简单动态字符串SDS集合底层实现原理zipListlistPackskipListquickListKey 与Value中元素的数量 本章重点 掌握Redis简单动态字符串了解Redis集合底层实现原理 简单动态字符串SDS SDS简介 我们Redis中无论是key还是value其数据类型都是字符串.我们Redis中的字符…...

OVS常用命令与使用总结
OVS常用命令与使用总结 说明 在平时使用ovs中,经常用到的ovs命令,参数,与举例总结,持续更新中… 进程启动 1.先准备ovs的工作目录,数据库存储路径等 mkdir -p /etc/openvswitch mkdir -p /var/run/openvswitch …...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
