分部积分法习题
前置知识:分部积分法
例题
计算积分 I n = ∫ [ ( x + a ) 2 + b 2 ] − k d x ( n ≥ 1 ) I_n=\int [(x+a)^2+b^2]^{-k}dx \quad(n\geq 1) In=∫[(x+a)2+b2]−kdx(n≥1)
解:
\qquad 用分部积分法,对任何自然数 k ≥ 1 k\geq 1 k≥1,有
I k = ∫ d x [ ( x + a ) 2 + b 2 ] d x = x + a [ ( x + a ) 2 + b 2 ] k + 2 k ∫ ( x + a ) 2 [ ( x + a ) 2 + b 2 ] k + 1 d x \qquad I_k=\int\dfrac{dx}{[(x+a)^2+b^2]}dx=\dfrac{x+a}{[(x+a)^2+b^2]^k}+2k\int\dfrac{(x+a)^2}{[(x+a)^2+b^2]^{k+1}}dx Ik=∫[(x+a)2+b2]dxdx=[(x+a)2+b2]kx+a+2k∫[(x+a)2+b2]k+1(x+a)2dx
= x + a [ ( x + a ) 2 + b 2 ] k + 2 k ∫ [ 1 ( ( x + a ) 2 + b 2 ) k − b 2 ( ( x + a ) 2 + b 2 ) k + 1 ] d x \qquad \qquad =\dfrac{x+a}{[(x+a)^2+b^2]^k}+2k\int[\dfrac{1}{((x+a)^2+b^2)^k}-\dfrac{b^2}{((x+a)^2+b^2)^{k+1}}]dx =[(x+a)2+b2]kx+a+2k∫[((x+a)2+b2)k1−((x+a)2+b2)k+1b2]dx
= x + a [ ( x + a ) 2 + b 2 ] k + 2 k I k − 2 k b 2 ⋅ I k + 1 \qquad \qquad =\dfrac{x+a}{[(x+a)^2+b^2]^k}+2kI_k-2kb^2\cdot I_{k+1} =[(x+a)2+b2]kx+a+2kIk−2kb2⋅Ik+1
由此可得 I k I_k Ik的递推公式为
I k + 1 = 1 2 k b 2 [ x ( x 2 + b 2 ) − k + ( 2 k − 1 ) I k ] I_{k+1}=\dfrac{1}{2kb^2}[x(x^2+b^2)^{-k}+(2k-1)I_k] Ik+1=2kb21[x(x2+b2)−k+(2k−1)Ik]
当 k = 1 k=1 k=1时,直接计算可得
I 1 = ∫ 1 ( x + a ) 2 + b 2 d x = 1 b ∫ d ( x + a b ) 1 + ( x + a b ) 2 = 1 b arctan ( x + a b ) + C I_1=\int \dfrac{1}{(x+a)^2+b^2}dx=\dfrac 1b\int \dfrac{d(\frac{x+a}{b})}{1+(\frac{x+a}{b})^2}=\dfrac 1b\arctan(\dfrac{x+a}{b})+C I1=∫(x+a)2+b21dx=b1∫1+(bx+a)2d(bx+a)=b1arctan(bx+a)+C
再由递推公式可得 I 2 , I 3 . … , I n I_2,I_3.\dots,I_n I2,I3.…,In的表达式。
相关文章:

分部积分法习题
前置知识:分部积分法 例题 计算积分 I n ∫ [ ( x a ) 2 b 2 ] − k d x ( n ≥ 1 ) I_n\int [(xa)^2b^2]^{-k}dx \quad(n\geq 1) In∫[(xa)2b2]−kdx(n≥1) 解: \qquad 用分部积分法,对任何自然数 k ≥ 1 k\geq 1 k≥1,…...
C++—非递归【循环】遍历二叉树(前序,中序,后序)思路讲解+代码实现
非递归遍历二叉树 前序中序后序 接下来我们在研究如何使用循环实现遍历二叉树时,以下面的二叉树为例: 在下文的讲解中,不对如何构建这颗二叉树做讲解,直接给出代码,如果有不懂的地方欢迎私信我。 文章中的完整源代码链…...
前端002_初始化项目
1、命名和启动项目 将目录名 vue-admin-template-master 重命名为 db-manager-system 将 db-manager-system/package.json 中的 name 值改为 db-manager-system {"name": "db-manager-system","version": "1.0.1","descriptio…...

组合设计模式
组合模式 组合模式定义使用场景1、文件系统的目录结构:2、组织架构图:3、菜单和菜单项:4、使用场景总结: 角色定义Component 抽象构件角色:Leaf 叶子构件:Composite 树枝构件: 需求背景代码实现Component(抽象构件角色…...
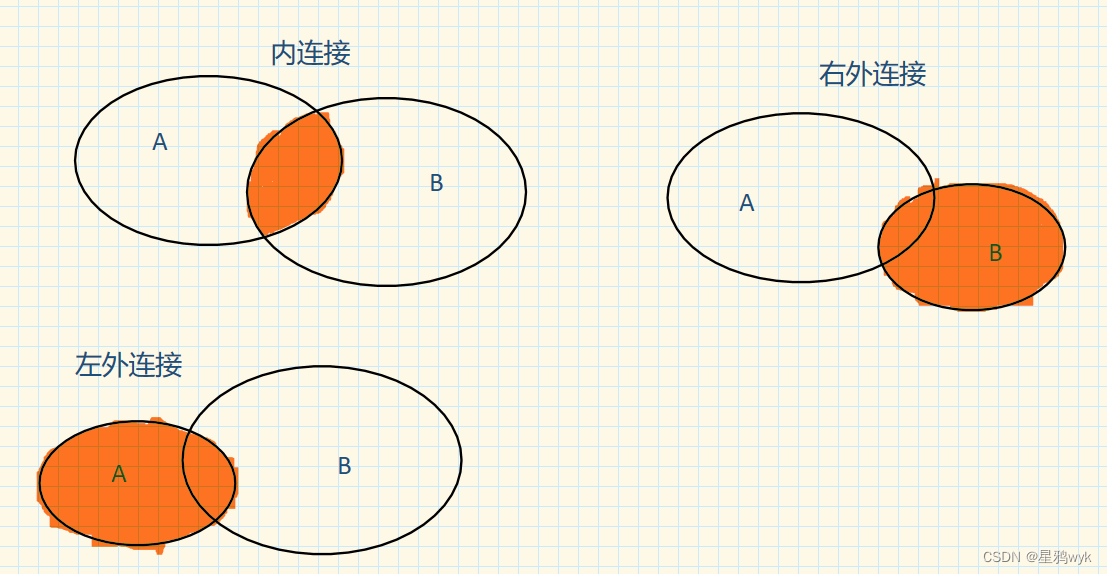
【MySQL】多表查询
上一篇介绍了外键约束,外键约束是用于连接两张数据表的,所以在此基础上就有了多表查询 之前的查询都是单表查询,这里我们会将多个数据表的数据结果返回在一张表上 文章目录 1.多表关系2.多表查询2.1 多表查询分类2.2 内连接2.3 外连接2.4 自连接2.5 联合查询2.6子查询 1.多表关…...

关于在线帮助中心你需要思考以下几个问题
搭建帮助中心是大多数企业都在尝试做的事情,它的重要性对于企业来说不言而喻。现在对于企业来说,搭建帮助中心或许不是什么难事,但是关于帮助中心,有几个问题需要思考清楚,才能让其发挥最大的价值。 一、如何让用户养成…...
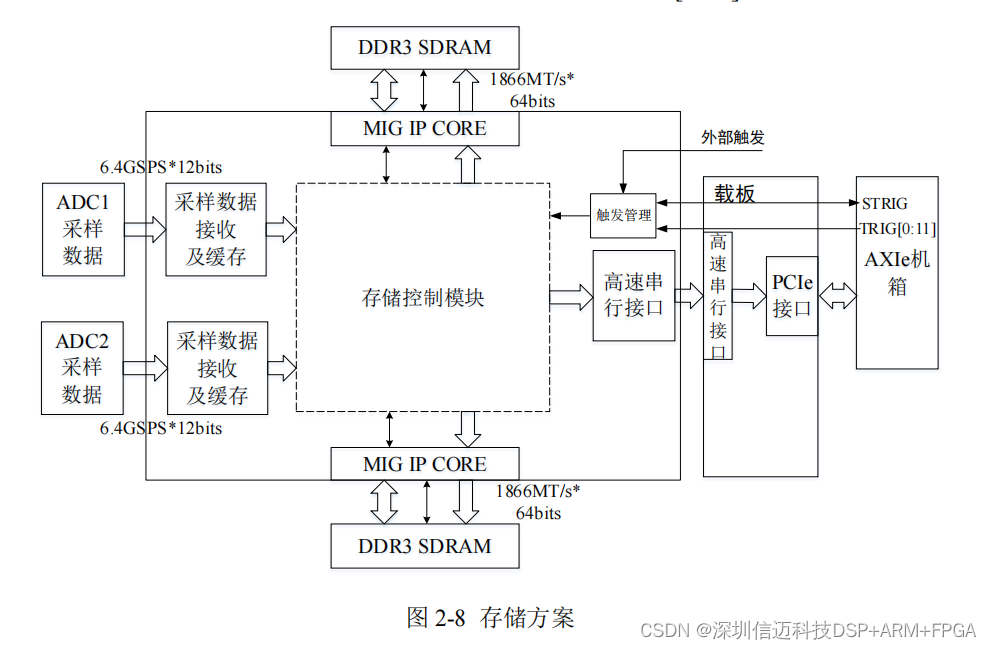
基于FPGA+JESD204B 时钟双通道 6.4GSPS 高速数据采集模块设计(一)总体方案
本章将根据高速数据采集指标要求,分析并确定高速数据采集模块的设计方 案,由此分析数据存储需求及存储速度需求给出高速大容量数据存储方案,完成 双通道高速数据采集模块总体设计方案,并综合采集、存储方案及 AXIe 接口需求 …...
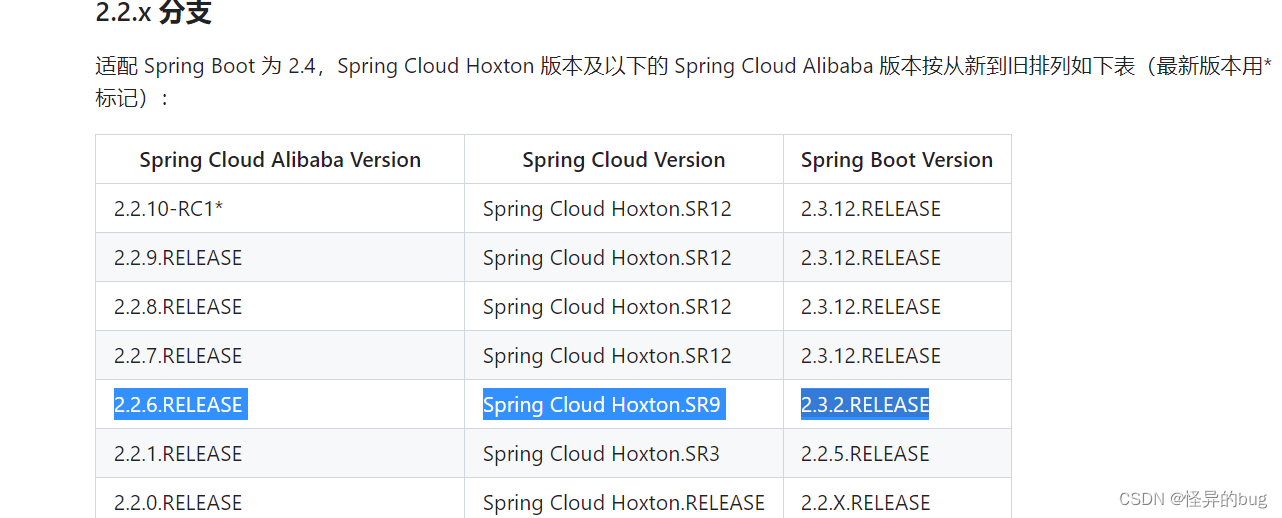
二、Spring Cloud Alibaba环境搭建
一、依赖环境 SpringCloud Alibaba 依赖 Java 环境来运行。还需要为此配置 Maven环境,请确保是在以下版本环境中安装使用。 64 bit JDK 1.8;Maven 3.2.x。 spring-cloud-alibaba相关网址: 地址:https://github.com/alibaba/spring-cloud-…...
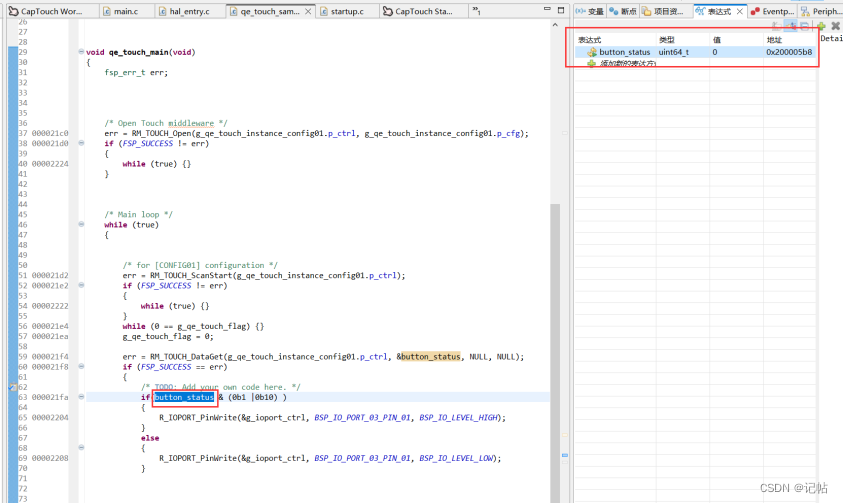
瑞萨e2studio(24)----电容触摸配置(1)
瑞萨e2studio.24--电容触摸配置1 概述硬件准备新建工程工程模板保存工程路径芯片配置工程模板选择时钟配置添加TOUCH驱动配置CapTouch开启调优界面启动 CapTouch 调优通过电容触摸点亮LED 概述 这篇文档将创建一个使用 e2 studio 集成 QE 的电容式触摸应用示例,通…...
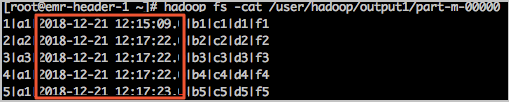
数据开发常见问题
目录 环境变量过多或者参数值过长时,为什么提交作业失败? 为什么Shell作业状态和相关的YARN Application状态不一致? 创建作业和执行计划的区别是什么? 如何查看作业运行记录? 如何在OSS上查看日志? 读…...

Ae:橡皮擦工具
橡皮擦工具 Eraser Tool 快捷键:Ctrl B 橡皮擦工具 Eraser Tool在工作原理上同 Ae 中的其它绘画工具(画笔、仿制图章)工具基本一致,都是通过绘制路径,然后基于此路径进行描边(可统称为“绘画描边”&…...

干货 | 正确引用参考文献的6大技巧
Hello,大家好! 这里是壹脑云科研圈,我是喵君姐姐~ 对于学术研究而言,正确引用参考文献非常重要。参考文献不仅展现了自己的学术水平,同时也给研究定位,突显研究在前人研究基础上作出的贡献。 …...

区块链系统探索之路:基于椭圆曲线的私钥与公钥生成
前两节我们探讨了抽象代数的重要概念:有限域,然后研究了基于椭圆曲线上点的怪异”“操作,两者表面看起来牛马不相及,实际上两者在逻辑上有着紧密的联系,简单来说如果我们在椭圆曲线上取一点G,然后让它跟自己做”“操作…...
)
Linux命令集(Linux常用命令--echo指令篇)
Linux命令集(Linux常用命令--echo指令篇) Linux常用命令集(echo指令篇)2.echo(echo)1. 输出自定义内容2. 禁止输出末尾换行符3. 转义功能4. 与特殊字符配合使用实现其余功能 Linux常用命令集(echo指令篇) 如…...
【电子学会】2023年03月图形化一级 -- 甲壳虫走迷宫
甲壳虫走迷宫 1. 准备工作 (1)绘制如图所示迷宫背景图,入口在左下角,出口在右上角,线段的颜色为黑色; (2)删除默认小猫角色,添加角色:Beetle; …...

老外从神话原型中提取的12个品牌个性
老外从神话原型中提取的12个品牌个性 也是西方视角,需要本土化 参照心理学大师荣格的理论:心理学潜意识派 趣讲大白话:品牌的调调是啥 【趣讲信息科技151期】 **************************** 12种原型又归属于4种人性动机。 1、稳定࿰…...

unity中的Quaternion.AngleAxis
介绍 unity中的Quaternion.AngleAxis 方法 Quaternion.AngleAxis() 函数是 Unity 引擎中的一个数学函数,用于创建一个绕着某个轴旋转一定角度的旋转四元数。在游戏开发中,经常会用到该函数来旋转物体或计算旋转后的方向向量。 该函数的函数原型为&…...
如何设置渗透测试实验室
导语:在本文中,我将介绍设置渗透实验室的最快方法。在开始下载和安装之前,必须确保你使用的计算机符合某些渗透测试的要求,这可以确保你可以一次运行多个虚拟机而不会出现任何问题。 在本文中,我将介绍设置渗透实验室的…...
-- Instant (时间戳类)(常用于Date与LocalDateTime的相互转化))
Java时间类(八)-- Instant (时间戳类)(常用于Date与LocalDateTime的相互转化)
目录 1. Instant的概述: 2. Instant的常见方法: 3. Date --->Instant--->LocalDateTime 4. LocalDateTime --->Instant--->Date 1. Instant的概述...

C++模板
模板是泛型编程的基础,泛型编程即以一种独立于任何特定类型的方式编写代码。模板的目的是为了提高复用性,将类型参数化,函数模板作用:建立一个通用函数,其函数返回值类型和形参类型可以不具体制定,用一个虚…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
