f(x)与|f(x)|,f ‘ (x),F(x)常见关系。
1.f(x)与|f(x)|关系。
1.连续关系。(f(x)在"[a,b]上连续" => |f(x)|在"[a,b]连续")
①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. (因为f(x)在x0的连续点=>x0必为|f(x)|的连续点)
注:”[a,b]连续“包括:①f(x)在[a,b]连续②f(x)在[a,b]上有界,且仅有有限间断点③f(x)在[a,b]只有有限个第一类间断点。
证明:f(x)在"[a,b]上连续" => |f(x)|在"[a,b]连续"

2.可积关系。(f(x)可积 => |f(x)|可积)
证明略。
反例:
f(x)有无限个间断点,f(x)不可积。但是|f(x)|可积。
3.可导关系。
①f(x)在x0可导,则当f(x0) ≠ 0时
f(x)可导 <=> |f(x)|可导
②f(x)在x0可导,则当f(x0) = 0时,有两种情况。
-------1.若f’(x₀) = 0,则 <=> |f(x)| 在点x₀处可导,且|f’(x₀)|=0。
-------2.若f’(x₀) ≠ 0,则| f(x)|在点x₀处不可导
证明当f’(x0) ≠ 0时,不成立。成立同样如此证明
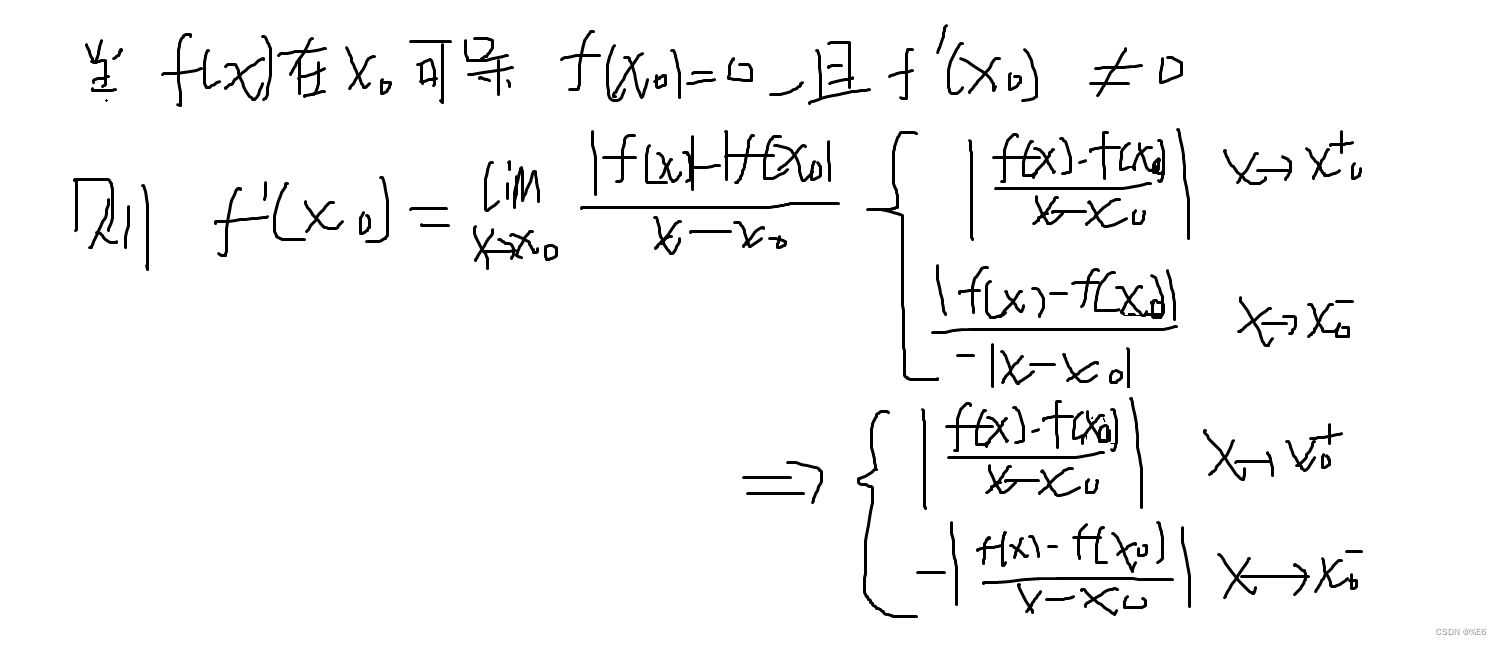
2.f(x)与f ’ (x)关系。
在有界区间(a,b)上有如下关系:
①f ‘(x)在(a,b)上有界 => f(x) 在(a,b)一定有界。
②f (x) 在(a,b)上无界 => f ’ (x)在(a,b)一定无界。
③设f(x) 在 x = a 处n阶可导,若当x - > a时f(x)是x - a 的n阶无穷小,则 f ’ (x)是 x - a 的n - 1 阶无穷小。
证明①:②类似

证明③:
在无界区间上没有确定性关系:
若f(x) = x,则f ’ (x) = 1在(a,+∞)有界,但f(x)在(a,+∞)无界。
若f(x) = sin2x,则f(x)在(a,+∞)有界,但是f ’ (x)在(a,+∞)无界。
3.f(x)与F(x)关系。
f(x)在(a,b)上有原函数F(x),则在(a,b)上:
①f(x)不一定连续
②f(x)不一定时初等函数
③F(x)不一定时初等函数
④F’(x) = f(x),因此F(x)连续
4.f(x)与其对应的变上限积分∫ f(t) dt(积分限a到x)关系。

①设x->a时候 , f(x) 是 x - a 的 n 阶无穷小。若f(x)连续,则 ”∫ f(t) dt(积分限a到x)(图片)“ 是 x - a 的 n + 1阶无穷小。
5.lim(x->x0)f’(x)与f’(x0)关系。
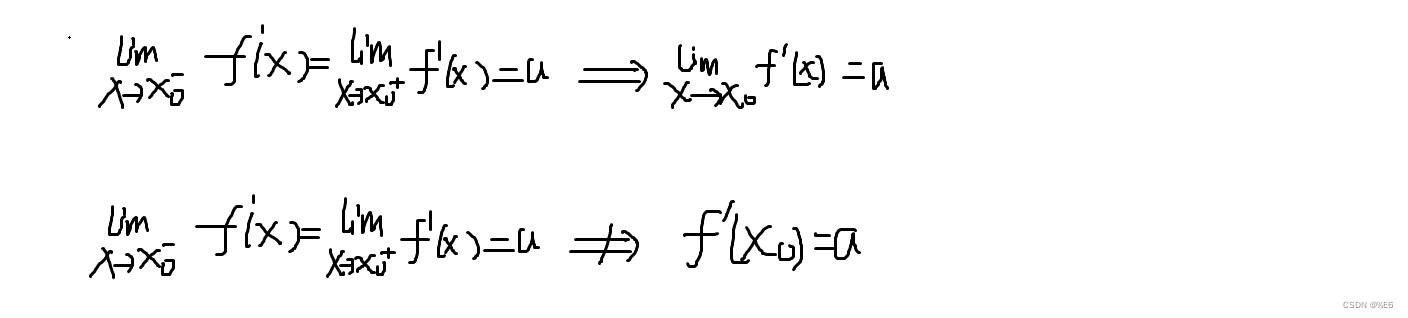
注意:连续的定义:如果f(x)在X0左右极限相等 <=> 在f(x) 在 X0连续 <=>该点的极限 = 该点的函数值。仅适用于f(x),而不适用于任意阶导数。
因为f(x)不能保证在 X0 点可导,甚至连续,极限存在都保证不了,故不能直接推出导数存在。
针对上述有总结以下情况:
1.f(x)在 X0 可导 => f(x) 在 X0 连续。(可导必连续)
2.lim f ’ (x) 存在 =/> f(x)在 X0 连续。(在 x -> X0时 上述有解释)
3.设 f (x) 在 x - > X0的空心领域内可导,且 lim f(x) = A (x -> X0) :
①若f(x) 在 x = x0 不连续 => f ’ (x0) 不存在。(不连续肯定不可导)
②若f(x) 在 x = x0 连续 => f’ (x0) = A。
证②:

4.设 f (x) 在 x - > X0的空心领域内可导,且 lim f ’ (x) = ∞ (x -> x0):
①若f(x) 在 x = x0 不连续 => f ’ (x0) 不存在。(不连续肯定不可导)
②若f(x) 在 x = x0 连续 => f’ (x0) = ∞ 。(仍然洛必达证)
5.设 f (x) 在 x - > X0的空心领域内可导,且 lim f ’ (x) = 不存在 (x -> x0):
看题,暂时没结论。
相关文章:

f(x)与|f(x)|,f ‘ (x),F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. (因为f(x)在x0的连续点>x0必为|f(x)|的连续点) 注:”[a,b]连续“包括&#…...

今天面了一个来字节要求月薪23K,明显感觉他背了很多面试题...
最近有朋友去字节面试,面试前后进行了20天左右,包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说,80%的人都会栽在第一轮面试,要不是他面试前做足准备,估计都坚持不完后面几轮面试。 其实&…...
)
如何使用二元三次回归分析建立预测模型?(分析、原理、代码示例)
二元三次回归是一种用于建立两个自变量与一个因变量之间关系的回归模型,常用于数据分析和预测。下面我会更详细地解释一下二元三次回归的原理、分析和示例代码。 1、原理 二元三次回归分析用多项式回归建立预测模型,其中包括两个自变量(通常…...
面向万物智联的应用框架的思考和探索(上)
原文:面向万物智联的应用框架的思考和探索(上),点击链接查看更多技术内容。 应用框架,是操作系统连接开发者生态,实现用户体验的关键基础设施。其中,开发效率和运行体验是永恒的诉求,…...

《Python机器学习基础教程》第1章学习笔记
目录 第1章 引言 1.1 为何选择机器学习 1.1.1 机器学习能够解决的问题 第1章 引言 机器学习又称为预测分析或统计学习,是一个交叉学科,是从数据中提取知识。 1.1 为何选择机器学习 智能应用早期,使用专家设计的规则体系来设计。 缺点&…...

ClickHouse 内存管理是如何实现的
概述 本文介绍Clickhouse内存管理的实现原理。通过本文的分析,可以对Clickhouse的内存管理有一个概要的理解。 Clickouse内存管理组成 ClickHouse 使用内存管理系统来控制内存资源的分配和释放。内存管理系统的主要组成部分是: 内存池:Cl…...

docker容器技术
什么是docker Docker 使用 Google 公司推出的 Go 语言 进行开发实现,基于 Linux 内核的 cgroup,namespace,以及 OverlayFS 类的 Union FS 等技术,对进程进行封装隔离,属于 操作系统层面的虚拟化技术。由于隔离的进程独…...
设计模式七大设计原则
文章目录 1、什么是设计模式2、单一职责原则3、开闭原则4、接口隔离原则5、依赖倒置原则6、迪米特法则(最少知道原则)7、里式替换原则8、组合优于继承 设计模式主要是为了满足一个字 变,这个字,可能是需求变更、可能是场景变更&a…...
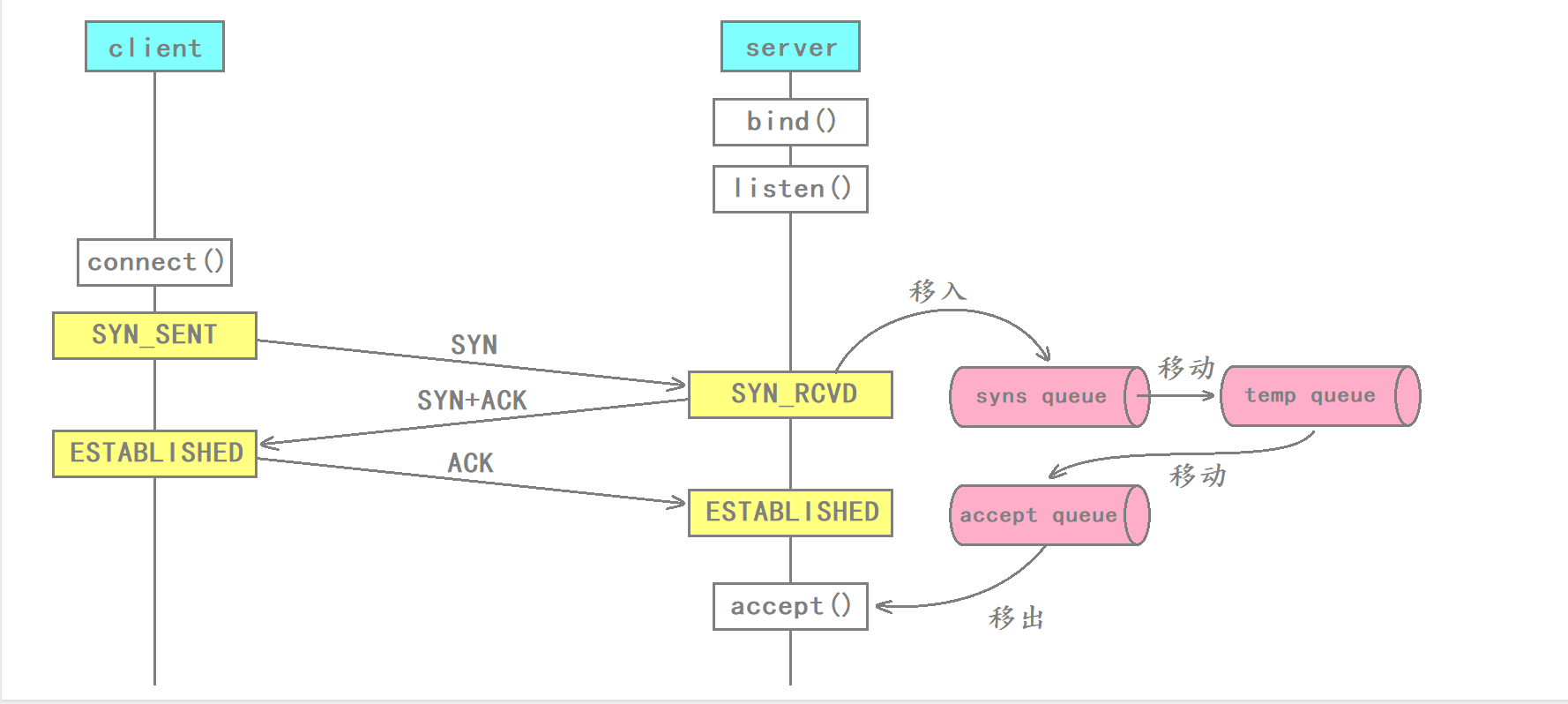
【Hello Network】TCP协议相关理解
作者:小萌新 专栏:网络 作者简介:大二学生 希望能和大家一起进步 本篇博客简介:补充下对于TCP协议的各种理解 TCP协议相关实验 TCP相关试验理解CLOSE_WAIT状态理解TIME_WAIT状态解决TIME_WAIT状态引起的bind失败的方法理解listen的…...

实施CRM目标有哪几步?如何制定CRM目标?
在当今竞争激烈的商业环境中,与客户建立持久的关系是企业重要的工作。CRM客户管理系统能有效帮助企业管理优化流程、管理客户,提高销售成功率,推动收入增长。那么您了解如何实施CRM吗?下面说说实施CRM目标是什么,如何设…...
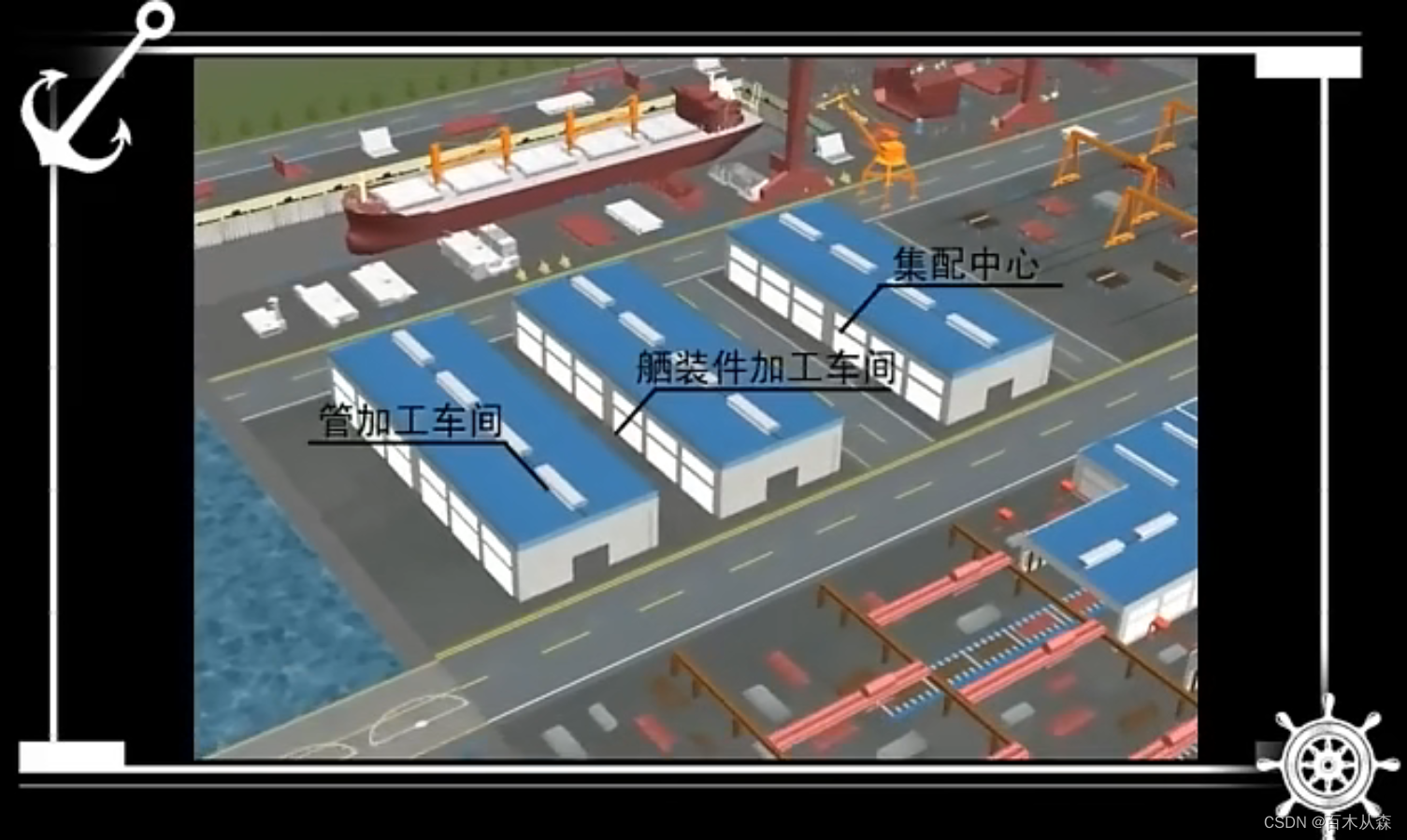
船舶建造概论(船舶建造工艺任务与现代造船模式)
船舶建造概论 1 船舶建造概论1.1 船舶建造工艺主要任务1.2 船舶建造流程(1)钢材料预处理(2) 钢材料加工(3)分段制作(4)总段制作(5)船台合拢(6&…...

项目内训(2023.5.6)
目录 Nacos是什么? 领域模型是什么? domain模块一般是干什么的? 在小乌龟中合并其他分支的作用是什么? nacos的配置文件 服务集群、服务提供、服务更加灵活庞大、消费服务、访问比较麻烦,A和B服务一起访问 系统结…...

【操作系统OS】学习笔记第二章 进程与线程(下)【哈工大李治军老师】
基于本人观看学习 哈工大李治军老师主讲的操作系统课程 所做的笔记,仅进行交流分享。 特此鸣谢李治军老师,操作系统的神作! 如果本篇笔记帮助到了你,还请点赞 关注 支持一下 ♡>𖥦<)!! 主页专栏有更多࿰…...
)
Linux命令集(Linux文件管理命令--rmdir指令篇)
Linux命令集(Linux文件管理命令--rmdir指令篇) Linux文件管理命令集(rmdir指令篇)5. rmdir(remove directory)1. 删除空的目录 folder12. 强制删除目录 folder1(包括非空目录)3. 递归删除目录及其目录下所有…...

在技术圈超卷的当下,学历到底是敲门砖还是枷锁?
前言 最近,突然之间被“孔乙己文学”刷屏了,短时间内“孔乙己文学”迅速走红,孔乙己是中国文学中的一位经典人物,他的长衫被认为是他的象征之一,孔乙己的长衫折射出很多现象,既有社会的,也有教育…...

Linux cgroup
前言 Cgroup和namespace类似,也是将进程进程分组,但是目的与namespace不一样,namespace是为了隔离进程组之前的资源,而Cgroup是为了对一组进程进行统一的资源监控和限制。 Cgroup的组成 subsystem 一个subsystem就是一个内核模…...
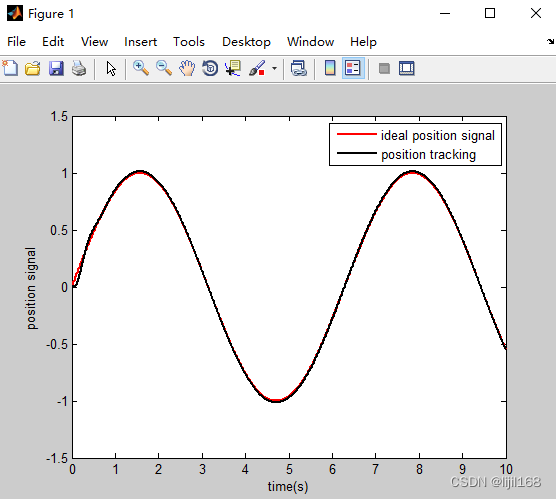
PID整定二:基于Ziegler-Nichols的频域响应
PID整定二:基于Ziegler-Nichols的频域响应 1参考2连续Ziegler-Nichols方法的PID整定2.1整定方法2.2仿真示例 1参考 1.1根轨迹图的绘制及分析 1.2计算机控制技术01-3.4离散系统的根轨迹分析法 1.3PID控制算法学习笔记 2连续Ziegler-Nichols方法的PID整定 2.1整定…...

【tkinter 专栏】专栏前言
文章目录 前言本章内容导图1. tkinter 工具及特点2. 为什么使用 Python 进行 GUI 设计?2.1 Python 可以做什么2.2 使用 tkinter 可以干什么?3. 如何学习使用 tkinter 进行 GUI 设计?4. 开发环境搭建4.1 Python 的版本4.2 安装 Python4.2.1 下载 Python 安装包4.2.2 安装 Pyt…...

解决Linux中文字体模糊的4种方法
在Linux中,字体是非常重要的一部分,因为它们直接影响到用户的视觉体验。如果Linux字体模糊不清,那么用户将很难阅读文本,这将极大地降低用户的工作效率。本文将介绍Linux Mint中文字体模糊的问题,并提供一些解决方案。…...
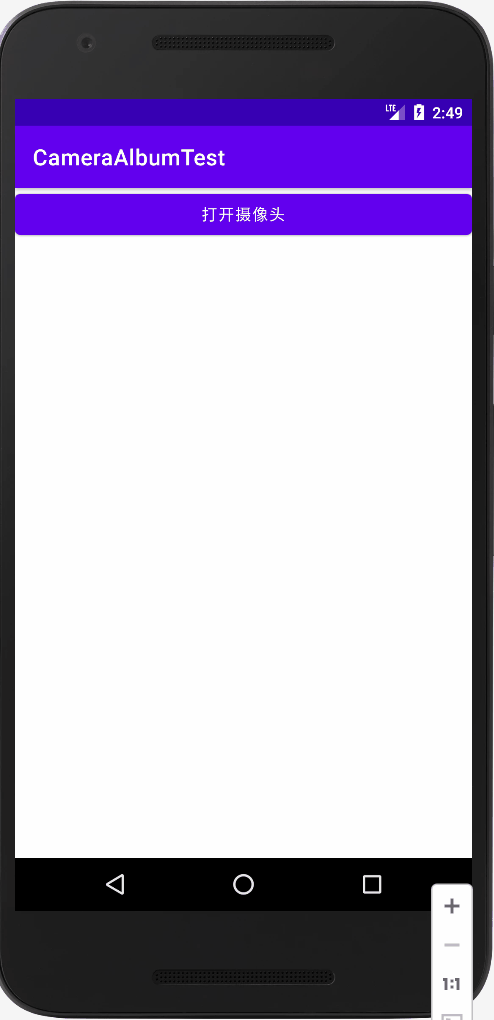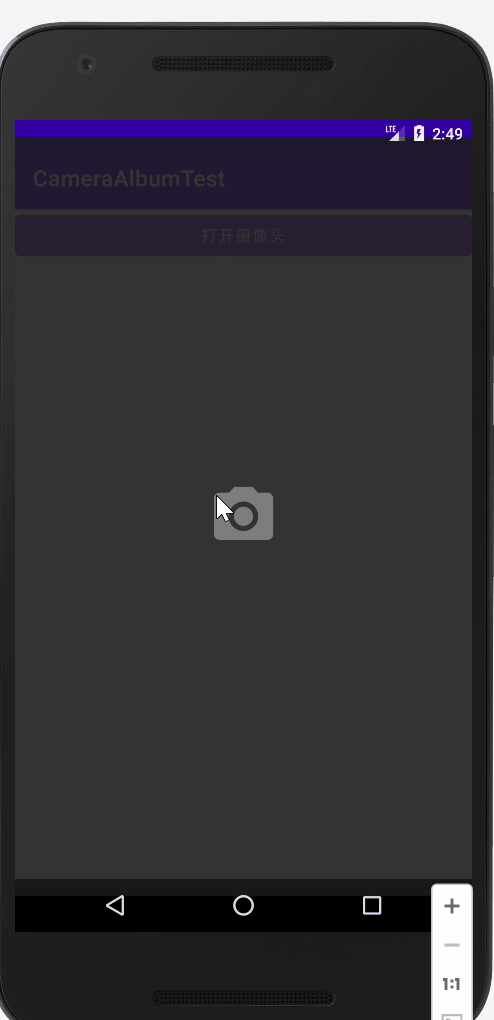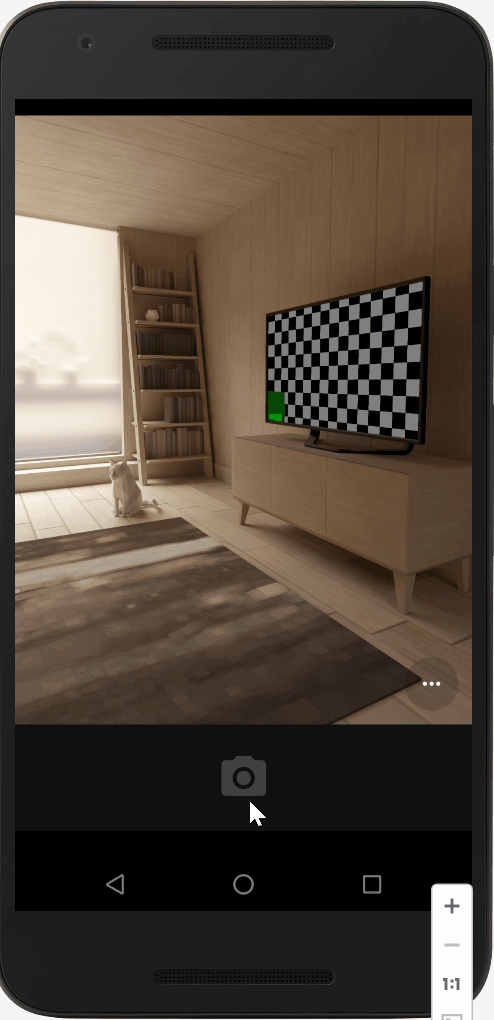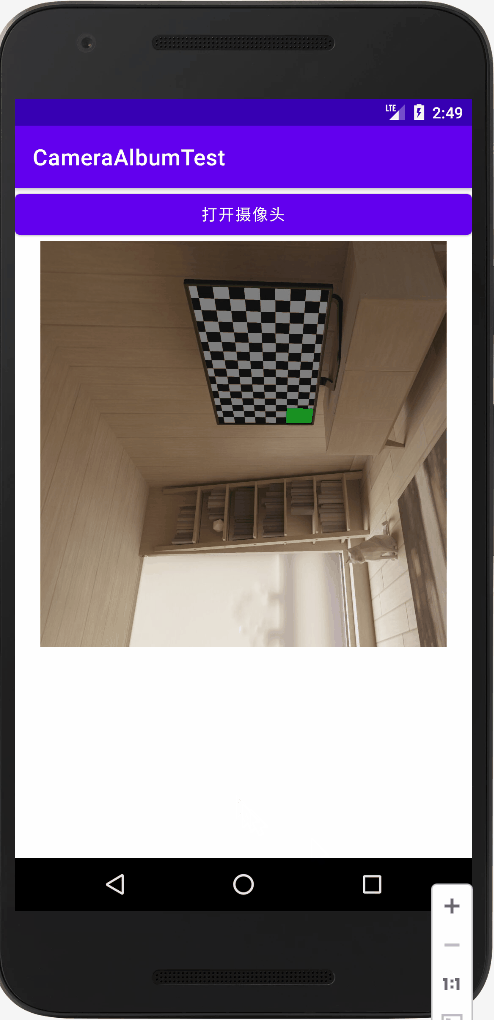
【Android入门到项目实战-- 7.3】—— 如何调用手机摄像头和相册
目录 一、调用摄像头拍照 二、打开相册选择照片 学完本篇文章可以收获如何调用手机的摄像头和打开手机相册选择图片功能。 一、调用摄像头拍照 先新建一个CameraAlbumTest项目。 修改activity_main.xml,代码如下: 按钮打开摄像头,ImageView将拍到的…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
