「Codeforces」D. Infinite Set
D. Infinite Set
https://codeforces.com/contest/1635/problem/D
题目描述
你有一个由不同正整数组成的数组和一个无限集 S,现在你需要往集合 S 中塞入所有符合 x x x 条件的数。
x x x 的条件(满足其中任意一个即可):
- x = a i ( 1 ≤ i ≤ n ) x = a_i(1\leq i\leq n) x=ai(1≤i≤n)
- x = 2 y + 1 ( y ∈ S ) x = 2y + 1 (y \in S) x=2y+1(y∈S) ( y y y 必须在 S 集合中)
- x = 4 y ( y ∈ S ) x = 4y (y \in S) x=4y(y∈S) ($y $ 必须在 S 集合中)
求无限集 S 中所有小于 2 p 2^p 2p 的个数。
输入描述
第一行包含两个整数 n 和 p (1≤n,p≤2⋅105)。
第二行包含 n 个整数 a1,a2,…,an (1≤ai≤109)。
保证 a 中的所有数字都是不同的。
输出描述
打印一个整数,即 S 中严格小于 2p 的元素数。 请记住以 109+7 为模打印。
样例
#1
2 4
6 1
9
#2
4 7
20 39 5 200
14
#3
2 200000
48763 1000000000
448201910
提示
在第一个示例中,小于 24 的元素是 {1,3,4,6,7,9,12,13,15}。
在第二个例子中,小于 27 的元素是 {5,11,20,23,39,41,44,47,79,80,83,89,92,95}。
解析
有一说一,二进制的题目我确实没写过…,一时间也只能想到暴力,可这样不可能过,后面看大佬题解,发现要用二进制…
**Tips:**以后但凡看到这种 2 p 2^p 2p 次幂的形式,要往二进制想想。
根据二进制, x x x 的第二和第三条件可以转为:
- 第一条件其实就是 A 数组的所有元素均属于 S
- 2 x + 1 2x+1 2x+1 相当于 2 < < 1 2 << 1 2<<1 然后加 1 1 1 (向后添加一个 1)
- 4 x 4x 4x 相当于 4 < < 2 4 << 2 4<<2 (向后添加两个 0)
题目要我们求 S 中所有小于 2 p 2^p 2p 的数,其实就是求对应的二进制最高位 1 的后面 0 的变化,例如 p = 3 p=3 p=3 时,对应二进制为 1000 1000 1000 ,我们可以得到且不保证符合的有 0000 、 0100 、 0110 、 0111 、 0010 、 0011 、 0001 0000、0100、0110、0111、0010、0011、0001 0000、0100、0110、0111、0010、0011、0001 。
通过上面的例子,我们发现,只是 1 后面的 0 发生了变化,而我们的规则是要么增加一个 1,要么增加两个0(这0是一起添加的,不能分开)。
我们假设一个数为 x x x ,那么我们可以得到:
| x x x 增加位数 | 得到的不同的数 | |
|---|---|---|
| 0 | x x x | 1 |
| 1 | x 1 x1 x1 | 1 |
| 2 | x 00 、 x 11 x00、x11 x00、x11 | 2 |
| 3 | x 001 、 x 100 、 x 111 x001、x100、x111 x001、x100、x111 | 3 |
| 4 | x 0000 、 x 1100 、 x 0011 、 x 1111 、 x 1001 x0000、x1100、x0011、x1111、x1001 x0000、x1100、x0011、x1111、x1001 | 5 |
上表意思:一个数的二进制在其后面增加若干位数,每次只能增加一个 1 或两个 0 ,那么最终得到的不同的数有多少个。
并且能发现,无论如何变化,它们都保证是唯一的。
看得出来这是个斐波那契数列 F [ i ] = F [ i − 1 ] + F [ i − 2 ] F[i] = F[i-1] + F[i-2] F[i]=F[i−1]+F[i−2] ,这里表示一个数增加 i i i 位可以得到的不同数的数量为 F [ i ] F[i] F[i] 个。
我们现在只是求了一个数增加若干位若得到的不同数,并没有将前面的也算进来,所以还需要对其做一个前缀和 p r e f i x [ i ] = p r e f i x [ i − 1 ] + F [ i ] prefix[i] = prefix[i-1] + F[i] prefix[i]=prefix[i−1]+F[i] ,此时定义变为 p r e f i x [ i ] prefix[i] prefix[i] 表示增加 i i i 位后所得到的所有不同数。
最后需要注意若一个数 a i a_i ai 可以由另外一个数得到 a j a_j aj ,因此为了不重复计算,所以只保留 a i a_i ai ,例如 A 有 2, 8 两个元素,8 可以通过 2 得到,因此我们只保留 2 即可。
2:0010
8:1000
0010 可以通过一次变化(即在尾部加两个 0 )==> 001000 ==> 1000
AC Code
public class Main {static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static StreamTokenizer st = new StreamTokenizer(br);static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));public static void main(String[] args) throws Exception {final int MOD = 1000000000 + 7;final int MAX = 200005;int n = nextInt(), p = nextInt(), ans = 0;int[] A = new int[MAX];int[] F = new int[MAX];int[] prefix = new int[MAX];F[0] = F[1] = 1;prefix[0] = 1; prefix[1] = 2;HashMap<Integer, Boolean> map = new HashMap<>();for(int i = 2; i < MAX; i++) {F[i] = (F[i-1] + F[i-2]) % MOD;prefix[i] = (prefix[i-1] + F[i]) % MOD;}for(int i = 1; i <= n; i++) {A[i] = nextInt();map.put(A[i], true);}// 对数组元素进行去重for(int i = 1; i <= n; i++) {int x = A[i];while(x != 0) {if(x % 2 == 1) x >>= 1; // 条件2,末尾加 1else if(x % 4 == 0) x >>= 2; // 条件3,末尾加两个 0else break;if(map.containsKey(x)) { // 判断 x 是否已经存在 S 中map.remove(A[i]); // 若存在,则表示 A[i] 可以通过其它元素得到,估抛弃该元素break;}}}Set<Integer> set = map.keySet();for(Integer x : set) {int bit = 32 - Integer.numberOfLeadingZeros(x); // 获取 x 二进制位数的前导零个数if(bit > p) continue;ans += prefix[p - bit];ans %= MOD;}System.out.println(ans);}public static int nextInt() throws Exception {st.nextToken();return (int) st.nval;}
}
相关文章:

「Codeforces」D. Infinite Set
D. Infinite Set https://codeforces.com/contest/1635/problem/D 题目描述 你有一个由不同正整数组成的数组和一个无限集 S,现在你需要往集合 S 中塞入所有符合 x x x 条件的数。 x x x 的条件(满足其中任意一个即可): x a i …...
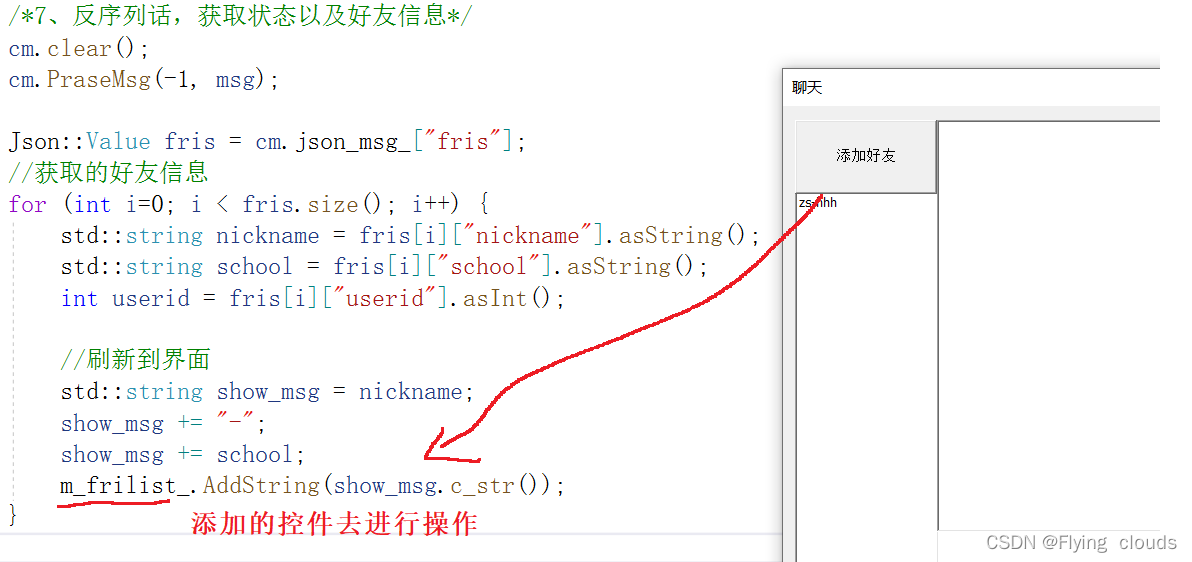
项目---基于TCP的高并发聊天系统
目录 服务端 服务端视角下的流程图 一、数据库管理模块 1.1 数据库表的创建 1.2 .对于数据库的操作 1.2.1首先得连接数据库 1.2.2执行数据库语句 1.2.3 返回数据库中存放的所有用户的信息 1.2.4返回数据库中存放的所有用户的好友信息 二、用户管理模块 2.1、UserInfo类&…...

iOS热更新-8种实现方式
一、JSPatch 热更新时,从服务器拉去js脚本。理论上可以修改和新建所有的模块,但是不建议这样做。 建议 用来做紧急的小需求和 修复严重的线上bug。 二、lua脚本 比如: wax。热更新时,从服务器拉去lua脚本。游戏开发经常用到。…...

R语言 | 编写自己的函数
目录 一、正式编写程序 二、设计第一个函数 三、函数也是一个对象 四、程序代码的简化 五、return()函数的功能 六、省略函数的大括号 七、传递多个参数函数的应用 7.1 设计可传递2个参数的函数 7.2 函数参数的默认值 7.3 3点参数“…”的使用 八、函数也可以作为参数 …...
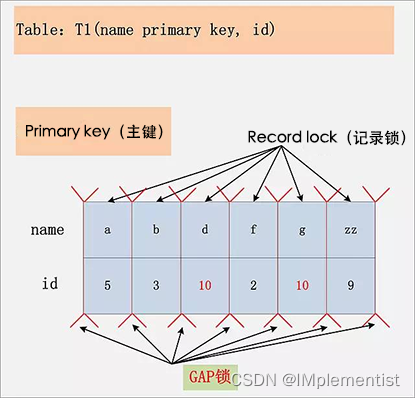
【Java校招面试】基础知识(七)——数据库
目录 前言一、数据库索引二、数据库锁三、数据库事务四、数据库连接池后记 前言 本篇主要介绍数据库的相关内容。 “基础知识”是本专栏的第一个部分,本篇博文是第六篇博文,如有需要,可: 点击这里,返回本专栏的索引文…...

MySQL高级--锁
一、锁 锁是计算机协调多个进程或线程并发访问某一资源的机制。在数据库中,除传统的计算资源(CPU、RAM、I/O)的争用以外,数据也是一种供许多用户共享的资源。如何保证数据并发访问的一致性、有效性是所有数据库必须解决的一个问题…...

Maven(六):Maven的使用——继承与聚合
Maven(六):Maven的使用——继承与聚合 前言一、实验九:继承1、概念2、作用3、举例4、操作4.1 创建父工程4.2 创建模块工程4.3 查看被添加新内容的父工程 pom.xml4.4 解读子工程的pom.xml4.5 在父工程中配置依赖的统一管理4.6 子工…...
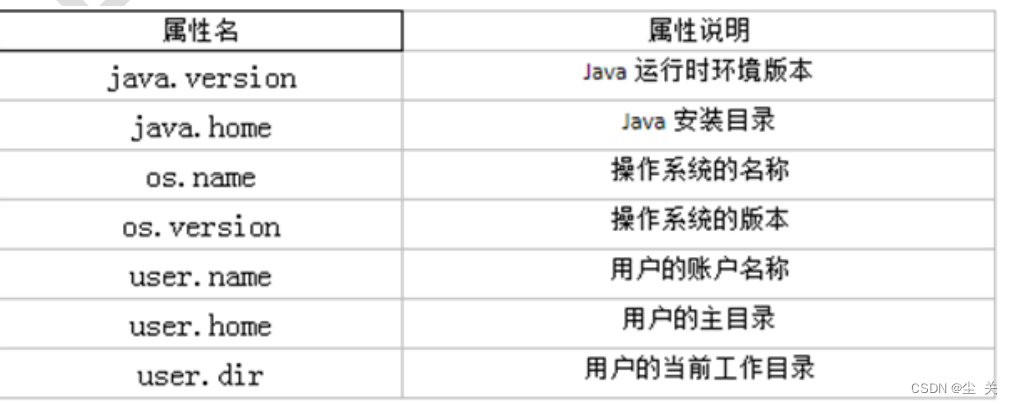
Java ---System类
System 类位于 java.lang 包,代表当前 Java 程序的运行平台,系统级的很多属性和控制方法都放置在该类的内部。由于该类的构造方法是 private 的,所以无法创建该类的对象,也就是无法实例化该类。 System 类提供了一些类变量和类方…...

代码随想录_贪心_leetcode 406 452
leetcode 406. 根据身高重建队列 406. 根据身高重建队列 假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高…...

C++类的静态成员详解:成员函数非静态成员函数的非法调用
在C中,静态成员是属于整个类的而不是某个对象,静态成员变量只存储一份供所有对象共用。所以在所有对象中都可以共享它。使用静态成员变量实现多个对象之间的数据共享不会破坏隐藏的原则,保证了安全性还可以节省内存。 静态成员的定义或声明要…...

Qt之滑动条和进度条(QSlider、QProgressBar)
文章目录 前言一、QSliderQSlider的常用API信号与槽 二、QProgressBar滑动条和滚动条的常用API 总结 前言 在用户界面设计中,滑动条和进度条是常见的控件。Qt中提供了QProgressBar和QSlider两个类来实现滚动条和滑动条。 一、QSlider 在Qt中,QSlider是…...
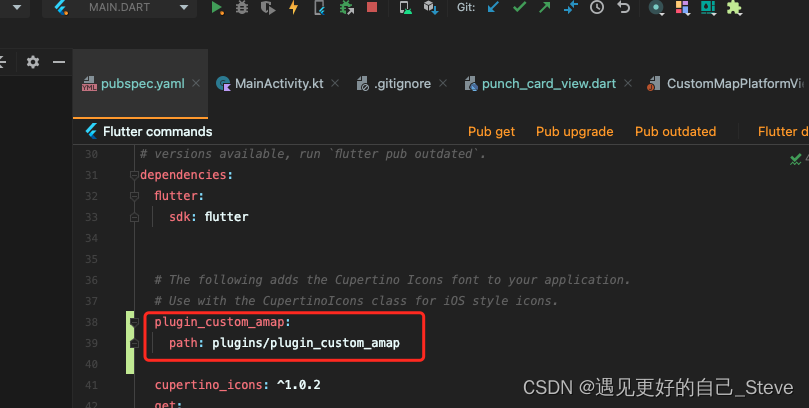
Flutter之插件开发plugin
目的:适用于独立业务模块,或者与原生页面交互频繁的地方。 基于flutter3.x , IDE :androidStudio demo:https://download.csdn.net/download/SHTLoveXX/87751845 步骤: 1.新建flutter project 【New flutter project】. 2. 在新建工程面板记得切换 …...
asp.net基于web的音乐管理网站dzkf17A9程序
本系统主要包含了等系统用户管理、公告信息管理、音乐资讯管理、音乐类型管理多个功能模块。下面分别简单阐述一下这几个功能模块需求。 管理员的登录模块:管理员登录系统对本系统其他管理模块进行管理。 用户的登录模块:用户登录本系统,对个…...

itop-3568开发板驱动学习笔记(25)设备树(四)GPIO 实例分析
《【北京迅为】itop-3568开发板驱动开发指南.pdf》 学习笔记 文章目录 GPIO 控制器必要属性其他属性 指定 GPIO 引脚 和时钟类似,GPIO 在设备树中也存在两层定义,首先是 GPIO 控制器,这部分由芯片原厂工程师编写,相当于 GPIO 底层…...
)
函数(定义、返回值、调用、参数)
目录 ❤ 无参函数 ❤ 有参函数 ❤ 空函数 ❤ 什么是返回值? ❤ 为什么要有返回值? ❤ 什么是函数调用? ❤ 为何用调用函数? ❤ 函数调用的三种形式 ❤ 形参和实参 形参 实参 ❤ 位置参数 位置形参 位置实…...

28. Kubernetes 核心组件讲解——API Server
本章讲解知识点 Kubernetes API Server 概述etcd 简介API Server 架构解析API Server 的 List-Watch 机制独特的 Kubernetes Proxy API 接口集群功能模板之间的通信1. Kubernetes API Server 概述 1.1 基本概念 Kubernetes API Server(API Server)是 Kubernetes 的核心组件…...
springboot框架开发医院云HIS 住院医生站、住院护士站功能实现
住院医生站主模块:包括医嘱管理、病案首页、分配入科、住院清单、我的质控等子模块 (1)医嘱管理功能简介 ①住院患者开立医嘱、支持医嘱复制、停止、作废等操作; ②医嘱类型含药品、项目、材料、嘱托; ③支持住院各…...

高性能定时器介绍及代码逐行解析--时间堆
简介 在《Linux高性能服务器编程》中,介绍了三种定时方法: socket选项SO_RCVTIMEO和SO_SNDTIMEOSIGALRM信号I/O复用系统调用的超时参数 基础知识 非活跃,是指客户端(这里是浏览器)与服务器端建立连接后,…...

汇编语言学习笔记五
div指令 除法, 被除数:默认是放在ax或者dx中,其位数为16位,则在ax中,如位数为32位,则高位在dx中,低位在ax中 除数:放在寄存器或者内存单元中,有8位和16位两种。 结果&am…...

Linux下的epf 是什么?
EPF (Extended Page Frame) 是 Linux 内核中的一个功能,它用于管理大内存系统中的物理页框。具体来说,当系统中的物理内存超过 1TB 时,传统的页表结构会变得非常庞大和复杂,给内存管理带来很大的困难。 EPF 架构通过将物理地址分…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
