6.1.1 图:基本概念
一,基本概念
1.基本定义
(1)图的定义

顶点集不可以是空集,但边集可以是空集。
(2)
有向图的表示:

圆括号
无向图的表示:

尖括号
简单图、多重图:

简单图:
(1)不存在重复边(2)不存在从顶点到自身的边
多重图:
(1)图G中某两个节点之间的边数多于一条
(2)允许通过同一条边与自己关联,则G为多重图
数据结构只探讨简单图
三,顶点的度。入度,出度

对于无向图:

顶点v的度是指依附于该顶点的边的条数,记为TD(V)
无向图的全部顶点的度的和等于边数的两倍
对于有向图:

入度是以顶点v为终点的有向边的数目,记为ID(v)
出度是以顶点v为起点的有向边的数目,记为OD(v)
顶点的度是其入度和出度之和。
四,顶点与顶点的关系描述
(1)路径——两个不同的顶点之间的顶点序列。
(2)简单路径:在路径序列中,顶点不重复出现的路径称为简单路径。
(3)点到点的距离:从顶点u出发到顶点v最短路径若存在,则此路径的长度称为从u到v的距离,若不存在此路径,距离记为无穷。

无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的。
有向图中中,若从顶点v到顶点w和顶点w和顶点v之间都有路径存在,则称v和w之间是强连通的。
这里的路径可以是很多条。

比如说A和B之间就是强连通的,而B和E之间就不是。
连通图和强连通图
1)特指无向图

2)特指有向图

常见考点:
1)对于n个积极点的无向图G
若G是连通图,则最少有n-1条边
若G是非联通图,则最多可能有
EP:
当有5个顶点的情况下:

地下四个顶点(两两相连)
上面一个顶点只要与下面任意一个顶点相连,就可以使之为连通图

2)

接下来我们学习子图:(研究图的局部)

1)理解子图的概念(首先必须是个图)
2)包含原图所哟有的vertex记为生成子图。(顶点集不可以是空集,边集可以是空集)
连通分量

1)连通 2)极大(包含尽可能多的顶点和边)
生成树:


若图中的顶点数为n,则它的生成树含有n-1条边。对于生成树,若看去他的一条边,则会变成非联通树,若加上一条边则会形成一个回路。
与生成树对应得是生成森林

实际应用:

几种特殊形态的图:


树和森林
n个顶点的树,必有n-1条边
n得顶点的图,若边数大于n-1,则是有回路的,那就不是树了。


相关文章:

6.1.1 图:基本概念
一,基本概念 1.基本定义 (1)图的定义 顶点集不可以是空集,但边集可以是空集。 (2) 有向图的表示: 圆括号 无向图的表示: 尖括号 简单图、多重图: 简单图:…...
SlickEdit for Windows and Linux crack
SlickEdit for Windows and Linux crack 现在可以在“新建注释”对话框中对颜色进行排序,使调色板中的颜色阵列看起来更符合逻辑。 在拆分或扩展行注释时添加了撤消步骤,这样您只需点击“撤消”一次即可撤消行注释扩展。 已更新VHDL颜色编码,…...
ChatGPT实现stackoverflow 解释
stackoverflow 解释 ChatGPT 公开服务以来,程序员们无疑是最早深入体验和"测试"的一批人。出色的效果也引发了一系列知识产权上的争议。著名的 stackoverflow 网站,就宣布禁止用户使用 ChatGPT 生成的内容来回答问题,一经发现&…...
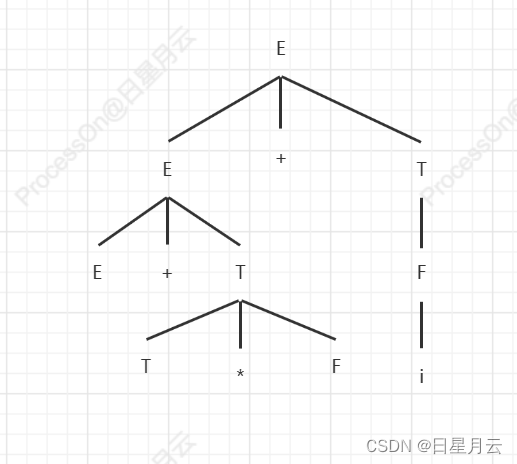
第五章 作业(123)【编译原理】
第五章 作业【编译原理】 前言推荐第五章 作业123 随堂练习课前热身04-17随堂练习04-17课前热身04-24 最后 前言 2023-5-3 22:12:46 以下内容源自《【编译原理】》 仅供学习交流使用 推荐 第四章 作业(123)【编译原理】 第五章 作业 1 1.令文法G为…...

基于Vue的个性化网络学习笔记系统
1.系统登录:系统登录是用户访问系统的路口,设计了系统登录界面,包括用户名、密码和验证码,然后对登录进来的用户判断身份信息,判断是管理员用户还是普通用户。 2.系统用户管理:不管是…...

如何搭建一个HTTP实验环境
这一讲是“破冰篇”的最后一讲,我会先简单地回顾一下之前的内容,然后在 Windows 系统上实际操作,用几个应用软件搭建出一个“最小化”的 HTTP 实验环境,方便后续的“基础篇”“进阶篇”“安全篇”的学习。 “破冰篇”回顾 HTTP …...

Electron 环境搭建
https://start.spring.io/ 在线数据分析网站 https://tj.aldwx.com/ https://www.spsspro.com/ win10如何分屏 拖到边缘 Electron 环境搭建 https://www.electronjs.org/zh/docs/latest/tutorial/%E6%89%93%E5%8C%85%E6%95%99%E7%A8%8B electron 隐藏菜单 electron 标题栏 设…...

农机电招平台~java
摘要 随着农机电招行业的不断发展,农机电招在现实生活中的使用和普及,农机电招行业成为近年内出现的一个新行业,并且能够成为大群众广为认可和接受的行为和选择。设计农机电招平台的目的就是借助计算机让复杂的销售操作变简单,变…...

springboot+vue体质测试数据分析及可视化设计(源码+文档)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的体质测试数据分析及可视化设计。项目源码以及部署相关请联系风歌,文末附上联系信息 。 💕💕作者&a…...
thinkphp+vue+html高校固定资产管理系统维修 租借4h80u
本高校资产管理系统采用的数据库是Mysql,使用thinkphp框架开发。在设计过程中,充分保证了系统代码的良好可读性、实用性、易扩展性、通用性、便于后期维护、操作方便以及页面简洁等特点。运行环境:phpstudy/wamp/xammp等 开发语言:php 后端框…...

【学习笔记】「北大集训 2021」经典游戏
我觉得很厉害。要是考场上能把这道题切了的话数据结构的水平肯定是不低的。 考虑简化版问题:如果只询问一个点的答案怎么做。 注意,我这么做是有风险的。我把战线拉长了。不过当然,如果连简化版的问题都做不了,那何谈正解&#…...
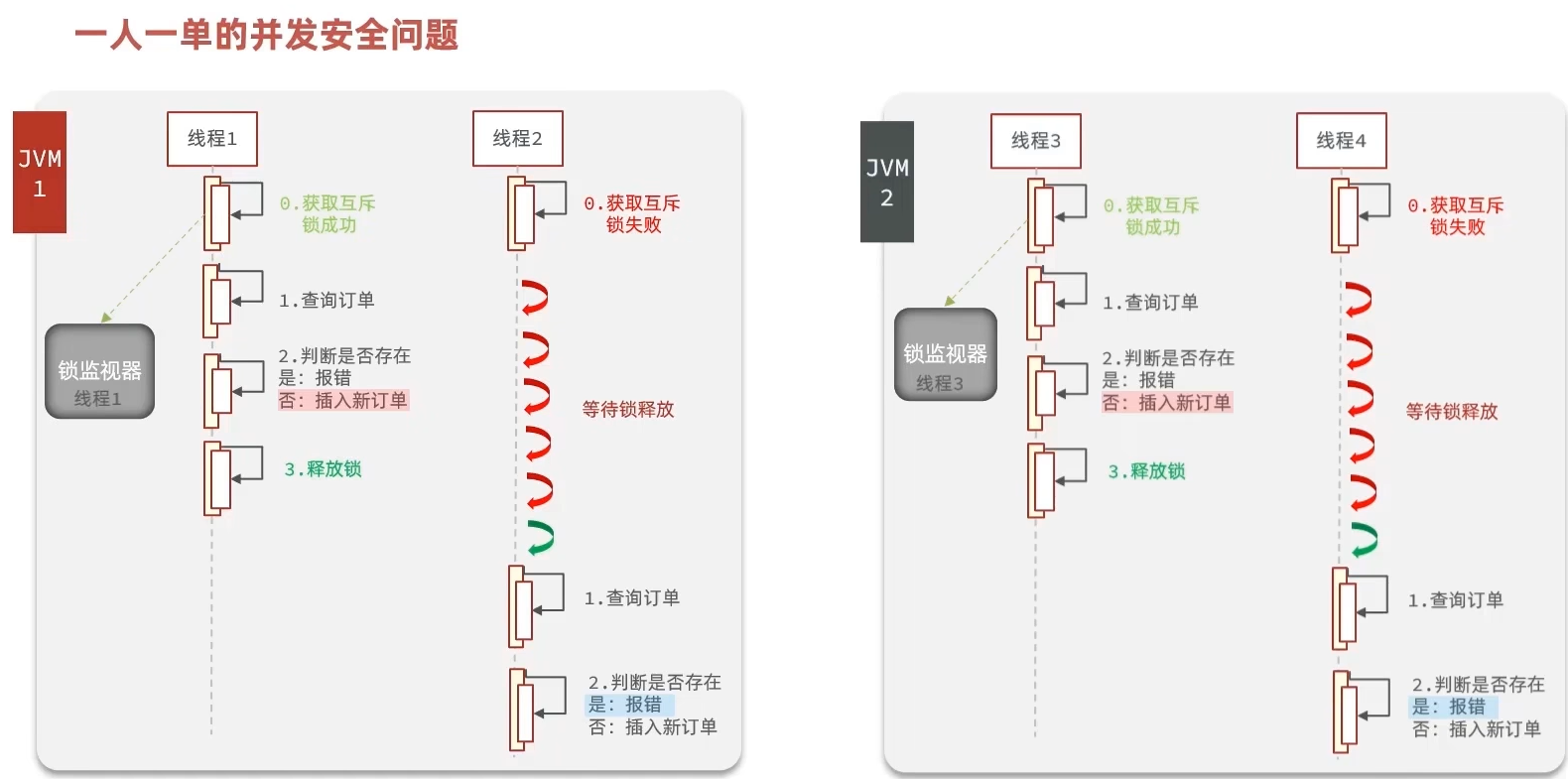
优惠卷秒杀功能、全局唯一ID、乐观锁解决超卖问题、悲观锁实现一人一单、集群下锁失效问题
文章目录 1 全局唯一ID的需求分析2 Redis实现全局唯一Id3 添加优惠卷4 实现秒杀下单5 库存超卖问题分析6 乐观锁解决超卖问题6 悲观锁实现一人一单7 集群环境下的并发问题 1 全局唯一ID的需求分析 每个店铺都可以发布优惠券: 当用户抢购时,就会生成订单…...

Nest的基本概念,以及如何使用Nest CLI来构建一个简单的Web应用程序
Nest是一个用于构建高效、可扩展的Node.js服务器端应用程序的框架。它是基于Express.js构建的,并且提供了多种新特性和抽象层,可以让开发者更加轻松地构建复杂的应用程序。 本文将介绍Nest的基本概念,以及如何使用Nest CLI来构建一个简单的W…...

15个创新世界119座城:1~10章音频
感恩每一个喜欢我文字的朋友,感恩每一次遇见。 最近后台总有朋友留言,能不能每一章配上音频,这样平时开车或挤地铁时也能听听。 谢谢你们在开车和挤地铁的时候都会产生听这本书的冲动。 五一抽空先把前十章的音频转录出来,希望你们…...

AI面试必刷算法题 附答案和解析 --持续更新中
面试中发现很多同学一股脑优化、润色项目经历,但聊到基本的算法,反而会一脸懵X,得空整理下算法题给大家,希望对你有帮助。 1. tail(head(tail(C))) ( ) 已知广义表: A(a,b), B(A,A), C(a,(b,A),B), 求下列运算的结果:(…...
聊一聊 GDB 调试程序时的几个实用命令
一:背景 1. 讲故事 用惯了宇宙第一的 Visual Studio 再用其他的开发工具还是有一点不习惯,不习惯在于想用的命令或者面板找不到,总的来说还是各有千秋吧,今天我们来聊一下几个在调试中比较实用的命令: 查看内存硬件…...

MySQL驱动对MYSQL进行update操作时返回值注意UseAffectedRows
数据库upate更新表时经常要用,update的结果进行一些逻辑判断,如返回值大于1表示更新成功,为0表示更新失败。 但是使用Mysql驱动连接数据库并进行update操作时,返回值可能不在预期。 update iwrs_drug_order set status2 where …...

OpenCV-Python图像几何变换
概念:几何变换是指将一幅图像映射到另外一幅图像内的操作。OpenCV提供了多个与映射有关的函数,这些函数使用起来方便灵活,能够高效地完成图像的映射。 缩放 cv2.resize()函数用于缩放图像 det cv2.resize(src, dsize[,dst[,fx[,fy[,interp…...
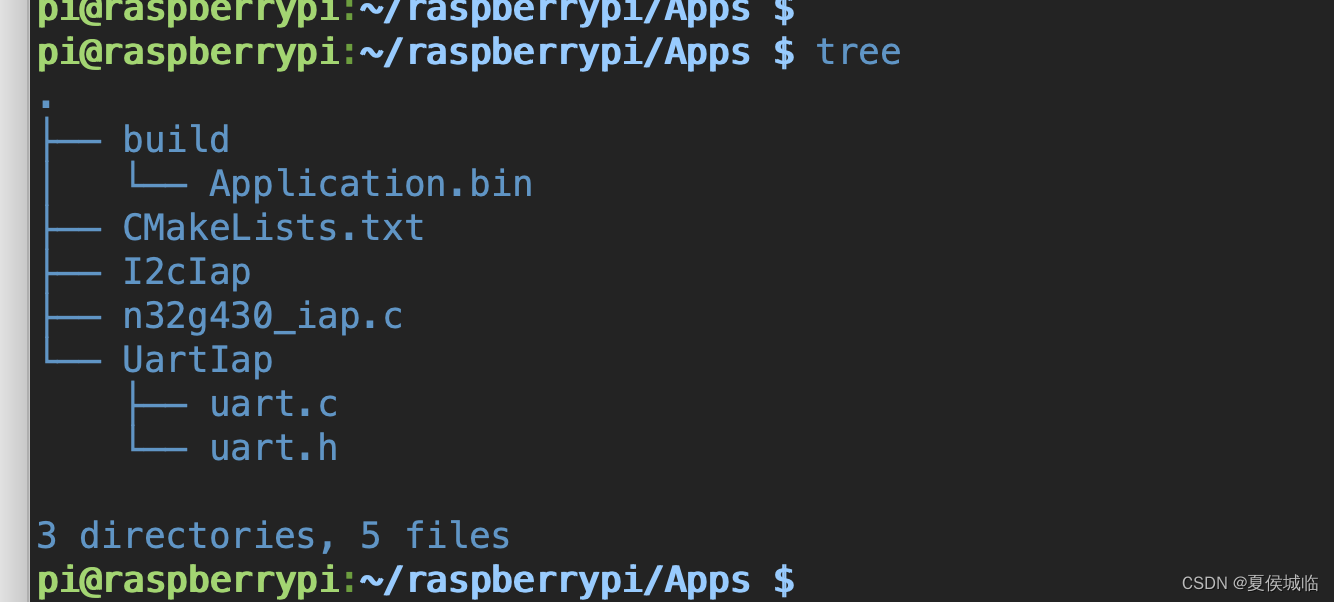
国民技术N32G430开发笔记(15)- IAP升级 树莓派串口发送数据
IAP升级 树莓派串口发送数据 1、树莓派接入usb转串口模块后,会生成/dev/ttyUSB0节点,因为树莓派内核已经编译usb_serial以及各模块的驱动。 我们直接对ttyUSB0节点编程即可。 2、协议同上一节 cmd data_lenght data0 … datax checksum 1、获取版本…...
svo论文解读
SVO: Semi-Direct Visual Odometry for Monocular and Multi-Camera Systems 2016TRO MOTION ESTIMATION 1 Sparse Image Alignment 从上一帧的特征投影到当前帧,最小化重投影误差计算帧间位姿(patch44) 2 Relaxation Through Feature Alig…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...
