【每日一题】1994.好子集的数目
1994.好子集的数目
- 题目描述
- 解决方案:状态压缩+动态规划
- 代码:Python
题目来源:LeetCode
原文链接:https://mp.weixin.qq.com/s/myI7_ZwJM7kizrwUtWgAZQ
难度级别:困难
题目描述
给你一个整数数组 nums。如果 nums 的一个子集中,所有元素的乘积可以表示为一个或多个 互不相同的质数 的乘积,那么我们称它为 好子集。
- 比方说,如果 nums = [1, 2, 3, 4] :
- [2, 3] ,[1, 2, 3] 和 [1, 3] 是 好 子集,乘积分别为 6 = 2 × 3 6 = 2 \times 3 6=2×3 , 6 = 2 × 3 6 = 2 \times 3 6=2×3 和 3 = 3 。
- [1, 4] 和 [4] 不是 好 子集,因为乘积分别为 4 = 2 × 2 4 = 2 \times 2 4=2×2 和 4 = 2 × 2 4 = 2 \times 2 4=2×2 。
请你返回 nums 中不同的 好 子集的数目对 1 0 9 + 7 10^9 + 7 109+7 取余 的结果。
nums 中的 子集 是通过删除 nums 中一些(可能一个都不删除,也可能全部都删除)元素后剩余元素组成的数组。如果两个子集删除的下标不同,那么它们被视为不同的子集。
示例1:
输入:nums = [1,2,3,4]
输出:6
解释:好子集为:
- [1,2]:乘积为 2 ,可以表示为质数 2 的乘积。
- [1,2,3]:乘积为 6 ,可以表示为互不相同的质数 2 和 3 的乘积。
- [1,3]:乘积为 3 ,可以表示为质数 3 的乘积。
- [2]:乘积为 2 ,可以表示为质数 2 的乘积。
- [2,3]:乘积为 6 ,可以表示为互不相同的质数 2 和 3 的乘积。
- [3]:乘积为 3 ,可以表示为质数 3 的乘积。
示例2:
输入:nums = [4,2,3,15]
输出:5
解释:好子集为:
- [2]:乘积为 2 ,可以表示为质数 2 的乘积。
- [2,3]:乘积为 6 ,可以表示为互不相同质数 2 和 3 的乘积。
- [2,15]:乘积为 30 ,可以表示为互不相同质数 2,3 和 5 的乘积。
- [3]:乘积为 3 ,可以表示为质数 3 的乘积。
- [15]:乘积为 15 ,可以表示为互不相同质数 3 和 5 的乘积。
提示:
- 1 < = n u m s . l e n g t h < = 1 0 5 1 <= nums.length <= 10^5 1<=nums.length<=105
- 1 < = n u m s [ i ] < = 30 1 <= nums[i] <= 30 1<=nums[i]<=30
解决方案:状态压缩+动态规划
题目乍看毫无头绪,但是仔细阅读之后,发现规定数组nums中的元素不超过30,因此可以将[1,30]中的整数分成如下三类:
- 对于任意一个好子集来说,添加任意数目的1,得到的新子集仍然是好子集;
- 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30:这些数均不包含平方因子,因此每个数在好子集中至多出现一次;
- 4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28:这些数包含平方因子,因此一定不能在好子集中出现。
首先,通过硬编码的方式把[1,30]中的整数按照上述分类,也可以先预处理出所有[1,30]中质数2, 3, 5, 7, 11, 13, 17, 19, 23, 29,再通过试除的方式动态分类。
分类完成后,就可以考虑使用动态规划了。由于每个质因数只能出现一次,并且[1, 30]中一共有10个质数,因此可以用一个长度为10的二进制数mask表示这些质因数的使用情况,其中mask的第 i 位为1,表示第 i 个质数已经被使用过了。
因此,定义 f [ i ] [ m a s k ] f[i][mask] f[i][mask]表示只选择[2,i]范围内的数,并且选择的数的质因数使用情况为mask时的方案数。
- 如果 i 本身包含平方因子,那么无法选择 i , 相当于在[2, i-1]范围内选择,状态转移方程为 f [ i ] [ m a s k ] = f [ i − 1 ] [ m a s k ] f[i][mask] = f[i-1][mask] f[i][mask]=f[i−1][mask]
- 如果 i 本身不包含平方因子,记其包含的质因子的二进制表示为subset(同样可以通过试除的方法得到),那么状态转移方程为 f [ i ] [ m a s k ] = f [ i − 1 ] [ m a s k ] + f [ i − 1 ] [ m a s k s u b s e t ] × f r e q [ i ] f[i][mask]=f[i-1][mask]+f[i-1][mask\\subset]\times freq[i] f[i][mask]=f[i−1][mask]+f[i−1][masksubset]×freq[i]其中:
- freq[i]表示数组nums中 i 出现的次数;
- mask\subset表示从二进制表示mask中去除所有在subset中出现的1,可以使用按位异或运算实现。这里需要保证subset是mask的子集,可以使用按位与运算来判断。
动态规划的边界条件为: f [ 1 ] [ 0 ] = 2 f r e q [ 1 ] f[1][0]=2freq[1] f[1][0]=2freq[1]即每一个在数组nums中出现的1都可以选或者不选。最终的答案即为所有 f [ 30 ] [ . . ] f[30][..] f[30][..]中除了 f [ 30 ] [ 0 ] f[30][0] f[30][0]以外的项的总和。
细节
注意到 f [ i ] [ m a s k ] f[i][mask] f[i][mask]只会从 f [ i − 1 ] [ . . ] f[i-1][..] f[i−1][..]转移而来,并且 f [ i − 1 ] [ . . ] f[i-1][..] f[i−1][..]中的下标总是小于mask,因此我们可以使用类似0-1背包的空间优化方法,在遍历mask时从 2 1 0 − 1 2^10-1 210−1到1逆序遍历,这样就只需要使用一个长度为 2 1 0 2^10 210的一维数组做状态转移了。
代码:Python
#!/usr/bin/env python
from collections import Counter
from typing import List# Hard level
class Solution:# 状态压缩动态规划def numberOfGoodSubsets(self, nums: List[int]) -> int:primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]mod = 10 ** 9 + 7freq = Counter(nums)f = [0] * (1 << len(primes))f[0] = pow(2, freq[1], mod)for i, occ in freq.items():if i == 1:continue# 检查 i 的每个质因数是否均不超过 1 个subset, x = 0, icheck = Truefor j, prime in enumerate(primes):if x % (prime * prime) == 0:check = Falsebreakif x % prime == 0:subset |= (1 << j)if not check:continue# 动态规划for mask in range((1 << len(primes)) - 1, 0, -1):if (mask & subset) == subset:f[mask] = (f[mask] + f[mask ^ subset] * occ) % modans = sum(f[1:]) % modreturn ansif __name__ == '__main__':today = Solution()nums = list(map(int, input('nums = ').strip().split(',')))print(today.numberOfGoodSubsets(nums))复杂度分析
- 时间复杂度: O ( n + C × O ( 2 π ( C ) ) O(n + C × O(2π(C)) O(n+C×O(2π(C))。其中 n 是数组 nums 的长度,C 是 nums 元素的最大值,在本题中 C = 30,π(x) 表示 ≤x 的质数的个数。
- 一共需要考虑 O ( C ) O(C) O(C)个数,每个数需要 O ( 2 π ( C ) ) O(2π(C)) O(2π(C))的时间计算动态规划;
- 在初始时需要遍历一遍所有的数,时间复杂度为 O ( n ) O(n) O(n)。
- 空间复杂度: O ( 2 π ( C ) ) O(2π(C)) O(2π(C)),即为动态规划需要使用的空间。
相关文章:

【每日一题】1994.好子集的数目
1994.好子集的数目 题目描述解决方案:状态压缩动态规划代码:Python 题目来源:LeetCode 原文链接:https://mp.weixin.qq.com/s/myI7_ZwJM7kizrwUtWgAZQ 难度级别:困难 题目描述 给你一个整数数组 nums。如果 nums 的一…...

坚持伙伴优先,共创数据存储新生态
4 月 26 日,2023 阿里云合作伙伴大会上,阿里巴巴集团董事会主席兼 CEO、阿里云智能集团 CEO 张勇表示,阿里云的核心定位是一家云计算产品公司,生态是阿里云的根基。让被集成说到做到的核心,是要坚定走向“产品被集成”…...
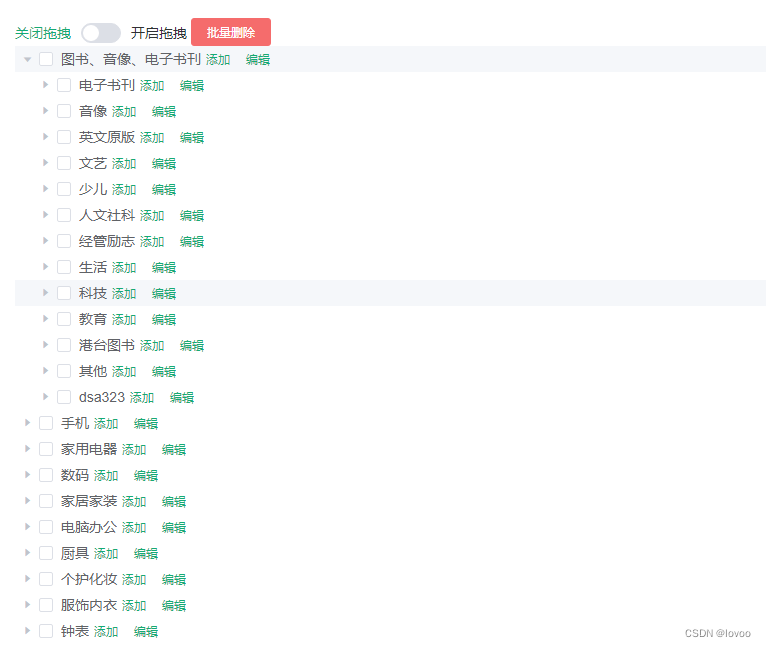
树形结构的三级分类如何实现?
概述: 本三级联动分类服务端使用的是: Springboot MyBatis-plus,前端使用的是:VueElementUI,树形控件使用的是el-tree。本三级联动分类可以把任一子项拖拽到其它目录,可以添加、编辑、删除分类。 效果图:…...

SSM整合完整流程
🏠个人主页:shark-Gao 🧑个人简介:大家好,我是shark-Gao,一个想要与大家共同进步的男人😉😉 🎉目前状况:23届毕业生,目前在某公司实习…...

虹科方案 | 助力高性能视频存储解决方案-2
上篇文章《虹科方案 | 助力高性能视频存储解决方案-1》我们分享了虹科&ATTO 和 Avid 共同创建协作解决方案,助力高性能视频存储,今天我们再深入介绍一下我们的案例详情。 一、行业挑战 从高端广播设施到小型独立工作室的媒体后期制作环境都需要允许多…...

java版深圳 工程管理系统软件 自主研发,工程行业适用 软件源码
Java版工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离 功能清单如下: 首页 工作台:待办工作、消息通知、预警信息,点击可进入相应的列表 项目进度图表:选择(总体或单个)项目显示…...
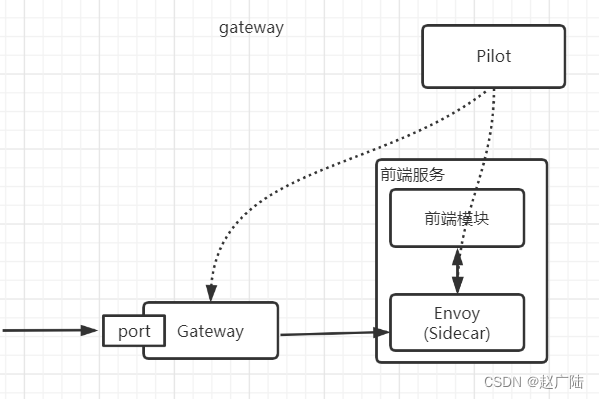
云原生Istio架构和组件介绍
目录 1 Istio 架构2 Istio组件介绍2.1 Pilot2.2 Mixer2.3 Citadel2.4 Galley2.5 Sidecar-injector2.6 Proxy(Envoy)2.7 Ingressgateway2.8 其他组件 1 Istio 架构 Istio的架构,分为控制平面和数据面平两部分。 - 数据平面:由一组智能代理([En…...
吹爆,全网第一个手把手教你从零开始搭建Spring Cloud Alibaba的笔记
Spring Cloud Alibaba 是阿里巴巴提供的微服务开发一站式解决方案,是阿里巴巴开源中间件与 Spring Cloud 体系的融合。 Springcloud 和 Srpingcloud Alibaba 区别? SpringCloud: 部分组件停止维护和更新,给开发带来不便;SpringCl…...

企业短信遭疯狂盗用,可能是没配置验证码
手机短信作为一种快捷的通讯方式被广泛应用。不仅在个人日常生活中,企业也习惯使用手机短信来进行验证和提醒,以保证业务的正常进行。随着数字化的发展,手机短信也成为了不法分子滥用的目标之一,给个人和企业带来不同经济损失。 个…...
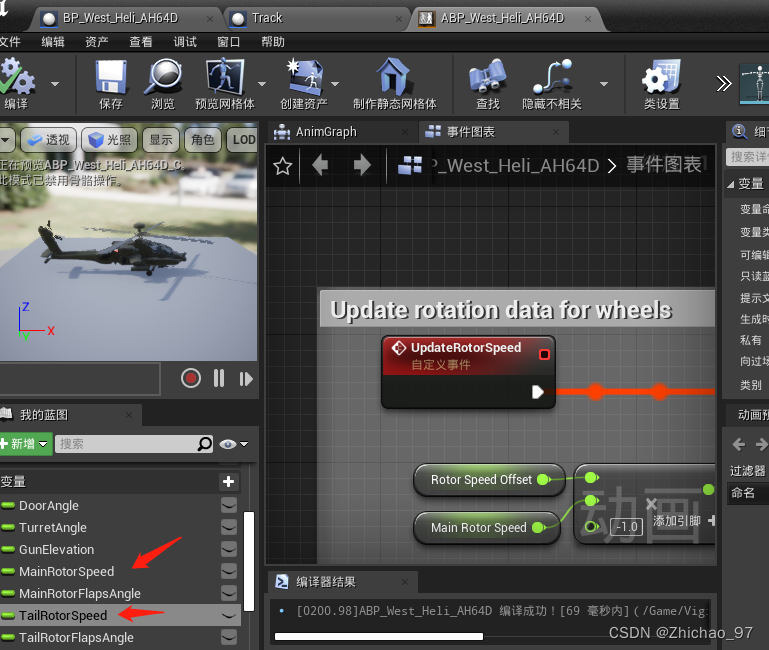
【UE】直升机沿样条线移动
效果 步骤 1. 将虚幻商城中的免费资产导入工程 下载完毕后可以看到如下文件 2. 新建一个Actor蓝图类,命名为“Track”,这个蓝图就是用来画样条线的 打开“Track”,添加样条组件 3. 打开“BP_West_Heli_AH64D” 在事件图表中先新建一个时间轴…...

GaussDB_200_6.5.1部署安装
目录 安装前准备 安装依赖 修改/etc/hosts 上传解压介质 预安装 拷贝安装包 预安装配置 编辑preinstall.ini配置文件 编辑host0配置文件 执行预安装命令 安装FusionInsight_Manager 修改install安装配置文件 执行安装命令 web操作安装数据库 GaussDB200测试 配…...

软件工具 | Python调用运筹优化求解器(一):以CVRPVRPTW为例
目录 1. 引言2. 求解器介绍3. 基础语言3.1 创建模型3.2 添加变量3.3 添加目标函数3.4 添加约束3.5 设置参数3.6 求解 4. 数学模型4.1 [CVRP数学模型](https://mp.weixin.qq.com/s/DYh-5WkrYxk1gCKo8ZjvAw)4.2 [VRPTW数学模型](https://mp.weixin.qq.com/s/tF-ayzjpZfuZvelvItue…...

如何在JAVA中实现网络编程?
在Java中实现网络编程通常需要使用Java提供的网络编程库——Java Networking API。Java Networking API支持常见的TCP和UDP协议,包括Socket、ServerSocket、DatagramSocket等类,通过这些类,我们可以创建、连接、监听和传输数据。 下面是在Ja…...

【redis】redis的缓存过期淘汰策略
【redis】redis的缓存过期淘汰策略 文章目录 【redis】redis的缓存过期淘汰策略前言一、面试题二、redis内存满了怎么办?1、redis默认内存是多少?在哪查看?如何修改?在conf配置文件中可以查看 修改,内存默认是0redis的默认内存有…...
ASP.NET动态Web开发技术第8章
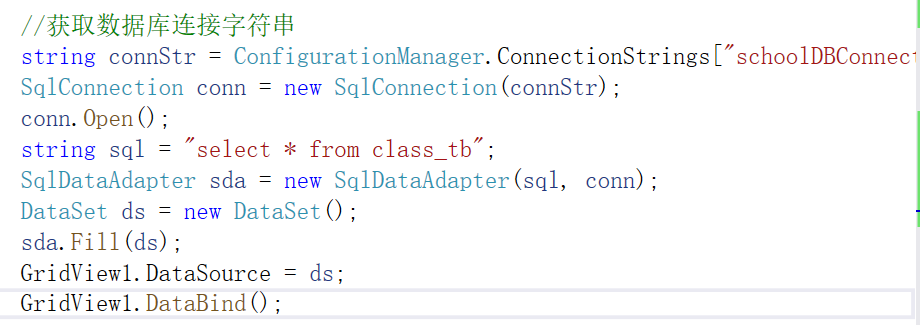
第8章ASP.NET数据访问 一.预习笔记 1.SqlDataSource控件 SqlDataSource数据源控件支持连接SQL关系数据库,它使用SQL命令来检索和修改数据。通常将SqlDataSource数据源控件与数据绑定控件一起使用。 属性1:ID:当前数据源控件的唯一标识符 …...
【旋转编码器如何工作以及如何将其与Arduino一起使用】
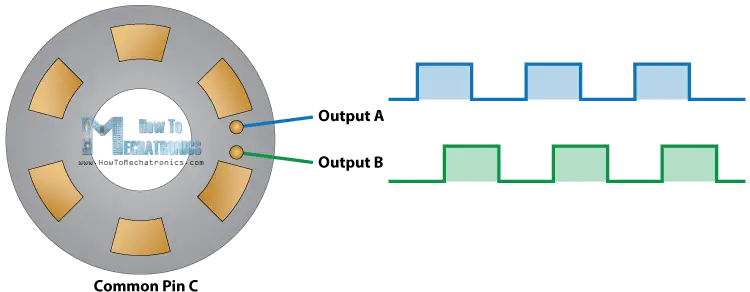
在本教程中,我们将学习旋转编码器的工作原理以及如何将其与Arduino一起使用。您可以观看以下视频或阅读下面的书面教程。 1. 概述 旋转编码器是一种位置传感器,用于确定旋转轴的角度位置。它根据旋转运动产生模拟或数字电信号。 有许多不同类型的旋转编码器按输出信号或传感…...

Tre靶场通关过程(linpeas使用+启动项编辑器提权)
Tre靶场通关 通过信息收集获得到了普通用户账号密码,利用PEASS-ng的linpeas脚本进行提权的信息收集,根据已有信息进行提权。 靶机下载地址: https://download.vulnhub.com/tre/Tre.zip 信息收集 靶机IP探测:192.168.0.129 a…...
java多线程下
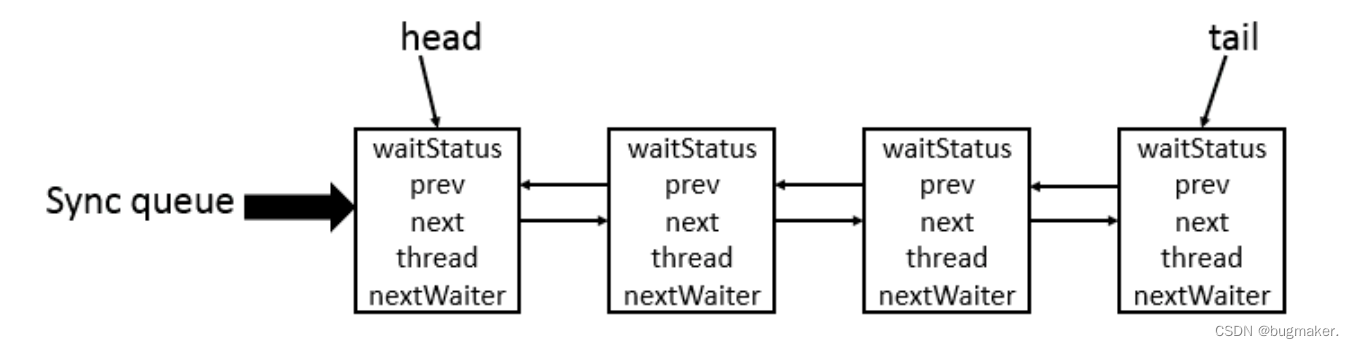
ThreadLocal ThreadLocal 有什么用?通常情况下,我们创建的变量是可以被任何一个线程访问并修改的。如果想实现每一个线程都有自己的专属本地变量该如何解决呢?JDK 中自带的ThreadLocal类正是为了解决这样的问题。 ThreadLocal类主要解决的就…...
使用无标注的数据训练Bert
文章目录 1、准备用于训练的数据集2、处理数据集3、克隆代码4、运行代码5、将ckpt模型转为bin模型使其可在pytorch中运用 Bert官方仓库:https://github.com/google-research/bert 1、准备用于训练的数据集 此处准备的是BBC news的数据集,下载链接&…...

《Netty》从零开始学netty源码(五十二)之PoolThreadCache
PoolThreadCache Netty有一个大的公共内存容器PoolArena,用来管理从操作系统中获得的内存,在高并发下如果所有线程都去这个大容器获取内存它的压力是非常大的,所以Netty为每个线程建立了一个本地缓存,即PoolThreadCacheÿ…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...
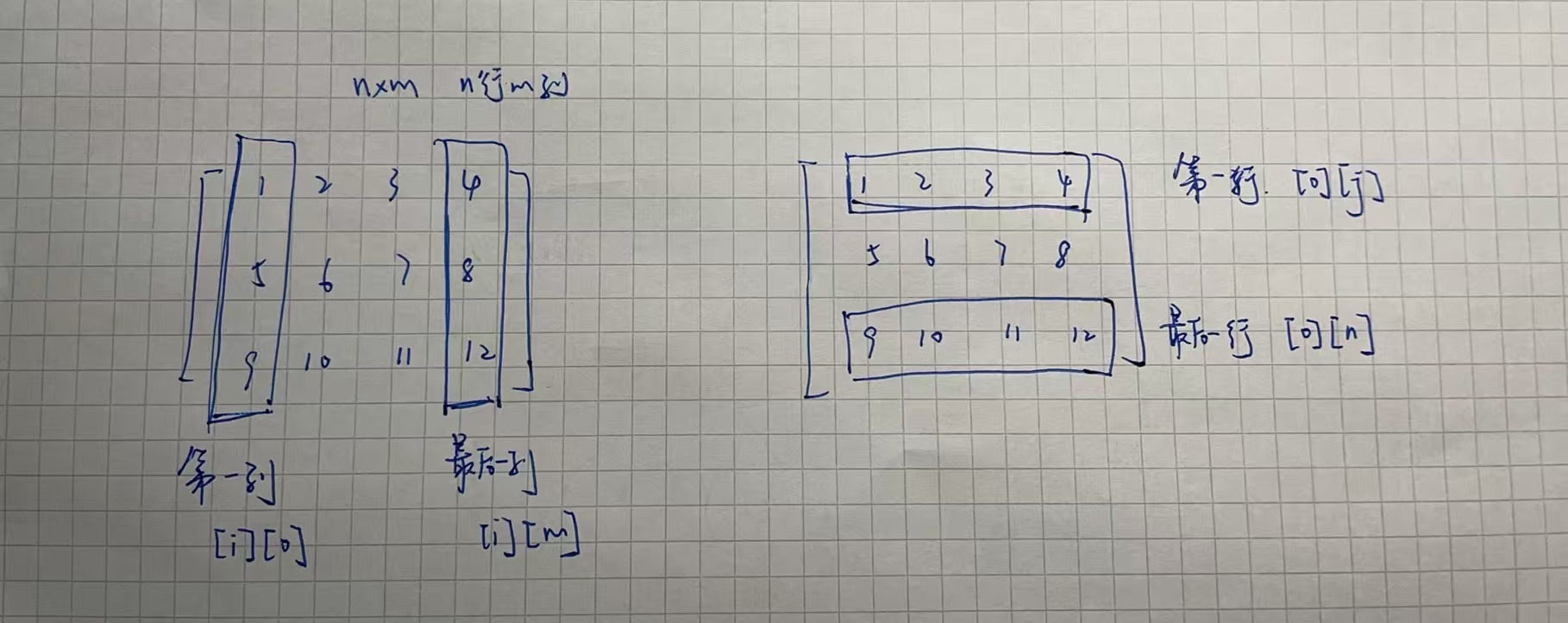
二维数组 行列混淆区分 js
二维数组定义 行 row:是“横着的一整行” 列 column:是“竖着的一整列” 在 JavaScript 里访问二维数组 grid[i][j] 表示 第i行第j列的元素 let grid [[1, 2, 3], // 第0行[4, 5, 6], // 第1行[7, 8, 9] // 第2行 ];// grid[i][j] 表示 第i行第j列的…...

Java多线程从入门到精通
一、基础概念 1.1 进程与线程 进程是指运行中的程序。 比如我们使用浏览器,需要启动这个程序,操作系统会给这个程序分配一定的资源(占用内存资源)。 线程是CPU调度的基本单位,每个线程执行的都是某一个进程的代码的某…...

调试快捷键 pycharm vscode
目录 调试快捷键 pycharm vscode 修改快捷键 方法 1:通过菜单打开 方法 2:用快捷键打开 调试快捷键 pycharm Resume Program F9 Step Over F8 两个离的比较近,比较方便,比vscode的好。 vscode Continue F5 改为F9 S…...

Qt Quick Dialogs模块功能及架构
Qt Quick Dialogs 是 Qt Quick 的一个附加模块,提供了一套用于创建和使用系统对话框的 QML 类型。在 Qt 6.0 中,这个模块经过了重构和增强。 一、主要功能和特点 1. 对话框类型 Qt Quick Dialogs 在 Qt 6.0 中提供了以下标准对话框类型: …...

民锋视角下的资金流效率与账户行为建模
民锋视角下的资金流效率与账户行为建模 在当前复杂多变的金融环境中,资金流效率已成为衡量一家金融服务机构专业能力的重要指标。民锋在账户管理与资金调配的实战经验中,逐步建立起一套以资金流路径为核心的行为建模方法,用以评估客户行为、交…...
