数据结构(六)—— 二叉树(7)构建二叉树
文章目录
- 如何使用递归构建二叉树
- 1、创建一颗全新树(题1-5)
- 2、在原有的树上新增东西(题6)
- 1 106 从 后序 与 中序 遍历序列构造二叉树
- 2 105 从 前序 与 中序 遍历序列构造二叉树
- 3 108 将有序数组转换为二叉搜索树(输入)
- 4 654 最大二叉树(输入很难想)
- 递归
- 单调栈
- 5 617 合并二叉树
- 6 701 二叉搜索树中的插入操作(重点独立重做)
- 7 450 删除二叉搜索树中的节点(中等题)
- 8 538 把二叉搜索树转换为累加树
如何使用递归构建二叉树
1、创建一颗全新树(题1-5)
构造树一般采用前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。
TreeNode* newtree = new TreeNode(val); // 每次递归都new一个节点
if(..) return newtree; // 直接返回这个root
newtree->left = 递归函数(....) // 用这个新建节点的左去接递归函数的返回值
newtree->right = 递归函数(....)
return newtree;
2、在原有的树上新增东西(题6)
删除二叉树节点,增加二叉树节点,用递归函数的返回值来完成。
输入为root
if (root == nullptr) {TreeNode* temp = new TreeNode(val); // 在树上新加的节点return temp;
}root->left = insertIntoBST(root->left, val);
root->right = insertIntoBST(root->right, val);return root; // return输入的root
1 106 从 后序 与 中序 遍历序列构造二叉树
1和2为同一类型,题外话:
前序和中序可以唯一确定一棵二叉树。
后序和中序可以唯一确定一棵二叉树。
但前序和后序不能唯一确定一棵二叉树!因为没有中序遍历无法确定左右部分,也就是无法分割。
设有一颗二叉树:
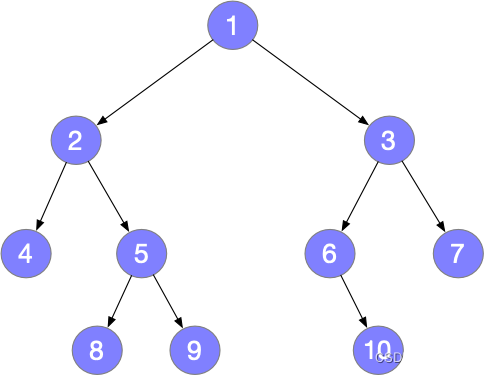
树的遍历结果可得两个规律:
1、在后序遍历序列中,最后一个元素为树的根节点
2、在中序遍历序列中,根节点的左边为左子树,根节点的右边为右子树
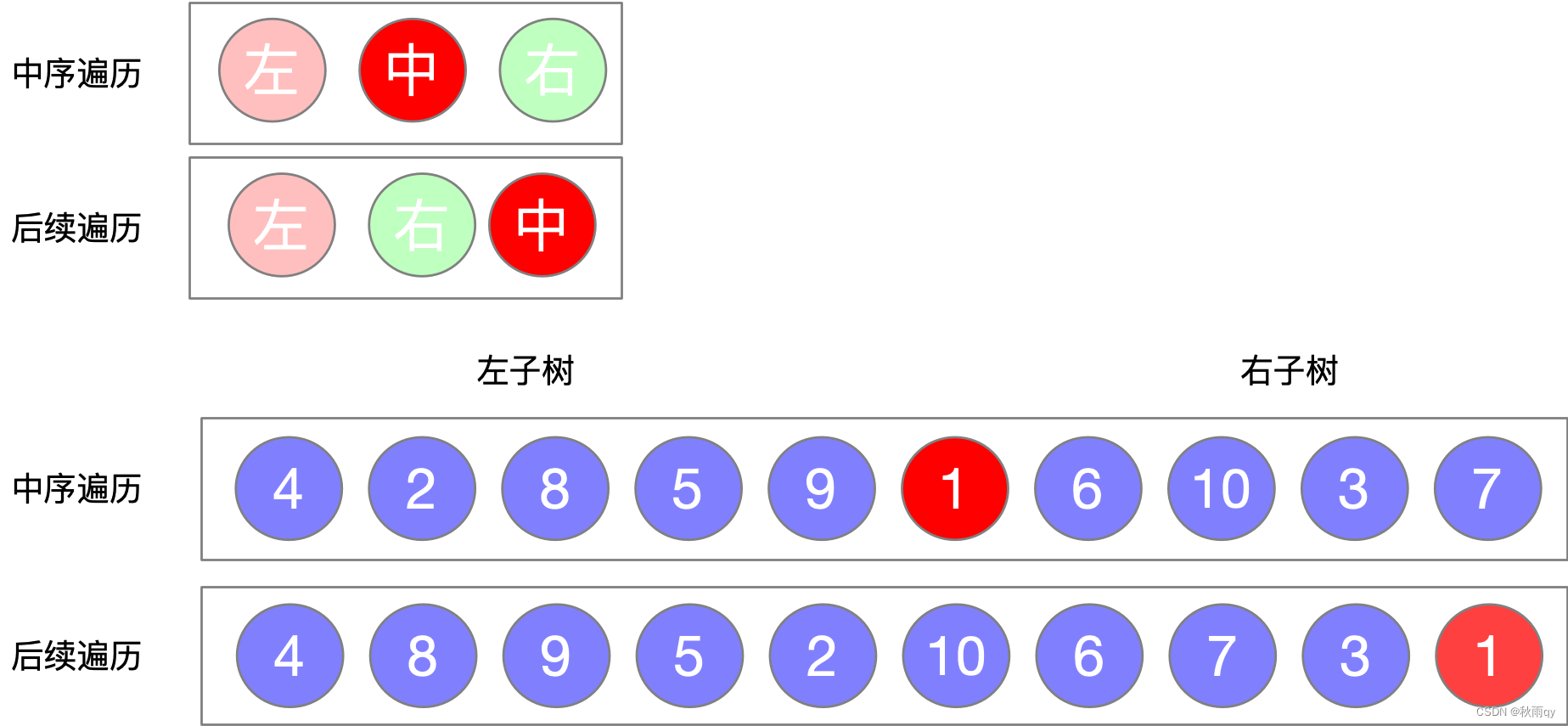
根据特性还原,步骤如下
1、输入中序和后序(如果是空数组就退)
2、处理后序:找到根节点(后序最后一个元素)(如果后序只有一个元素了直接返回)
3、处理中序:中序中根节点的位置
4、将中序分为左、右子树
5、得到后序的左、右子树
6、子树作为下一次递归的输入
步骤拆解伪代码如下:
// 第一步
if (postorder.size() == 0) return NULL;// 第二步:后序遍历数组最后一个元素,就是当前的中间节点
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// 叶子节点
if (postorder.size() == 1) return root;// 第三步:确认根节点在中序中的位置
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;
}// 第四步:切割中序数组,得到 中序左数组和中序右数组
// 第五步:切割后序数组,得到 后序左数组和后序右数组// 第六步
root->left = traversal(中序左数组, 后序左数组);
root->right = traversal(中序右数组, 后序右数组);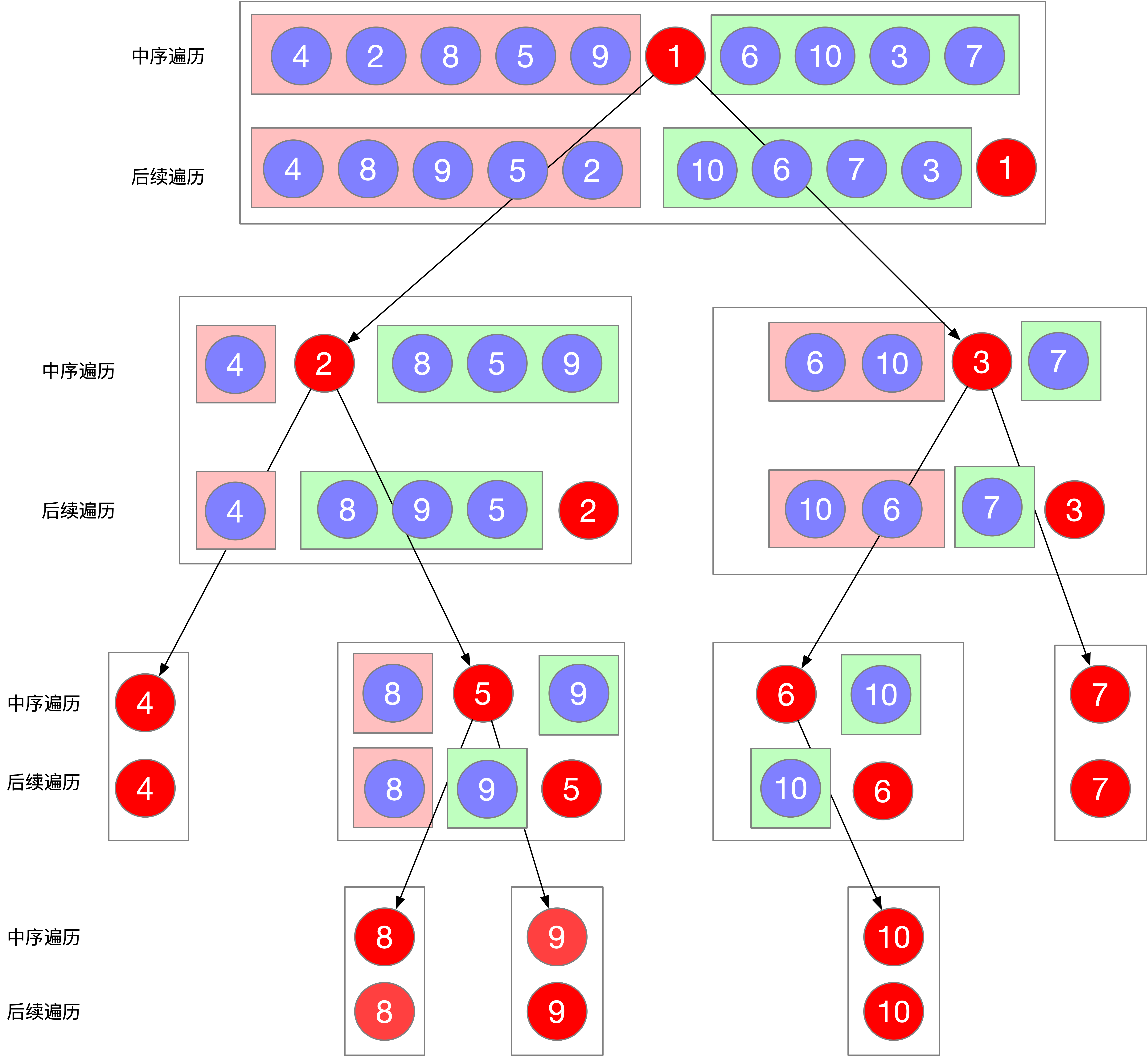
第4和第5尤其重要,如何将输入的中序和后序分割为中序左右树和后序左右树尤为关键
4、将中序分割左右子树
// 找到根节点在中序中的位置(中序的切割点)
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;
}// 左闭右开区间:[0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end) 注意这里加1,因为要跳过根节点,下面分割后序不加。
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end());
5、后序数组的切割点怎么找?
后序的根节点在最后,不像中序可以靠根节点来分割左右子树。
此时有一个必然条件,中序数组大小一定是和后序数组的大小相同的,后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
// postorder 舍弃末尾元素,因为这个元素就是中间节点,已经用过了
postorder.resize(postorder.size() - 1);// 左闭右开,注意这里使用了左中序数组大小作为切割点:[0, leftInorder.size)
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
// [leftInorder.size(), end) 注意这里不加1,前面分割中序时加
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
整体代码如下
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int sizeinorder = inorder.size();int sizepostorder = postorder.size();if (sizepostorder == 0) return nullptr;int rootValue = postorder[sizepostorder - 1]; // 根节点的值TreeNode* newtree = new TreeNode(rootValue);if (sizepostorder == 1) return newtree;int delimiterIndex;for (delimiterIndex = 0; delimiterIndex < sizeinorder; delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}vector<int> inorderleft(inorder.begin(), inorder.begin() + delimiterIndex);vector<int> inorderright(inorder.begin() + delimiterIndex + 1, inorder.end());vector<int> postorderleft(postorder.begin(), postorder.begin() + inorderleft.size());vector<int> postorderright(postorder.begin() + inorderleft.size(), postorder.end() - 1);newtree->left = buildTree(inorderleft, postorderleft);newtree->right = buildTree(inorderright, postorderright);return newtree;
}
2 105 从 前序 与 中序 遍历序列构造二叉树
注意看分割时的索引
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int sizepreorder = preorder.size();int sizeinorder = inorder.size();if (sizepreorder == 0) return nullptr;int rootval = preorder[0];TreeNode* newtree = new TreeNode(rootval);if (sizepreorder == 1) return root;int inrootindex;for (inrootindex = 0; inrootindex < sizeinorder; ++inrootindex) {if (inorder[inrootindex] == rootval) break;}vector<int> inorderleft(inorder.begin(), inorder.begin() + inrootindex);vector<int> inorderright(inorder.begin() + inrootindex + 1, inorder.end());vector<int> preorderleft(preorder.begin() + 1, preorder.begin() + 1 + inorderleft.size());vector<int> preorderright(preorder.begin() + 1 + inorderleft.size(), preorder.end());newtree->left = buildTree(preorderleft, inorderleft);newtree->right = buildTree(preorderright, inorderright);return newtree;
}
3 108 将有序数组转换为二叉搜索树(输入)
二分法复习,数组的mid就是根节点
1、输入输出
TreeNode* construct(vector<int>& nums, int left, int right)
输入一个数组nums,返回一个从nums[left]到nums[right]的元素构建一棵树
2、左指针大于右指针退出递归
if (left > right) return nullptr;
3、使用二分法找到这一区间[left, right]中的中间值mid,记为nums[mid],从而确定根节点的值。(本质就是寻找分割点,分割点作为当前节点,然后递归左区间和右区间)
问题:数组长度为偶数,中间节点有两个,取哪一个?实际上取哪一个都可以,答案都对。
int mid = (left + right) / 2;,这么写其实有一个问题,就是数值越界,例如left和right都是最大int,这么操作就越界了,在二分法中尤其需要注意!求mid写做:int mid = left + ((right - left) / 2);
int mid = left + ((right - left) / 2);
TreeNode* newtree = new TreeNode(nums[mid]);
newtree->left = traversal(nums, left, mid - 1);
newtree->right = traversal(nums, mid + 1, right);
return newtree;
4、整合
class Solution {
private:TreeNode* traversal(vector<int>& nums, int left, int right) {if (left > right) return nullptr;int mid = left + ((right - left) / 2);TreeNode* root = new TreeNode(nums[mid]);root->left = traversal(nums, left, mid - 1);root->right = traversal(nums, mid + 1, right);return root;}public:TreeNode* sortedArrayToBST(vector<int>& nums) {TreeNode* root = traversal(nums, 0, nums.size() - 1);return root;}
};
4 654 最大二叉树(输入很难想)
递归
构造树一般采用前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。
1、输入输出
TreeNode* construct(vector<int>& nums, int left, int right)
输入一个数组nums,返回一个从nums[left]到nums[right]的元素构建一棵树
2、左指针大于右指针退出递归
if (left > right) return nullptr;
3、找到这一区间[left, right]中的最大值的索引maxindex,记为nums[maxindex],这样确定根节点的值,随后进行递归。
int maxindex = left;
for (int i = left + 1; i <= right; ++i) {if (nums[i] > nums[maxindex]) {maxindex = i;}
}
// 找最大值索引TreeNode* node = new TreeNode(nums[maxindex]);
node->left = construct(nums, left, maxindex - 1);
node->right = construct(nums, maxindex + 1, right);
return node;
4、整合
class Solution {
public:TreeNode* bfs(vector<int>& nums, int left, int right){if(left > right){return nullptr;}int maxindex = left;for(int i = left + 1; i <= right; ++i){if(nums[i] > nums[maxindex]) maxindex = i;}TreeNode* newtree = new TreeNode(nums[maxindex]);newtree->left = bfs(nums, left, maxindex-1);newtree->right = bfs(nums, maxindex+1, right);return newtree;}TreeNode* constructMaximumBinaryTree(vector<int>& nums) {return bfs(nums, 0, nums.size()-1);}
};
单调栈
之后补充
5 617 合并二叉树
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if (root1 == nullptr && root2 == nullptr) return nullptr;if (root1 == nullptr) return root2;if (root2 == nullptr) return root1;TreeNode* newtree = new TreeNode(root1->val + root2->val);newtree->left = mergeTrees(root1->left, root2->left);newtree->right = mergeTrees(root1->right, root2->right);return newtree;
}
6 701 二叉搜索树中的插入操作(重点独立重做)
在原有的树上新增东西
TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == nullptr) {TreeNode* temp = new TreeNode(val);return temp;}// TreeNode* temp = new TreeNode(root->val);if (root->val > val) {root->left = insertIntoBST(root->left, val);}if (root->val < val) {root->right = insertIntoBST(root->right, val);}// return temp;return root;
}
7 450 删除二叉搜索树中的节点(中等题)
8 538 把二叉搜索树转换为累加树
相关文章:

数据结构(六)—— 二叉树(7)构建二叉树
文章目录 如何使用递归构建二叉树1、创建一颗全新树(题1-5)2、在原有的树上新增东西(题6) 1 106 从 后序 与 中序 遍历序列构造二叉树2 105 从 前序 与 中序 遍历序列构造二叉树3 108 将有序数组转换为二叉搜索树(输入…...

安装适用于Linux的Windows11子系统(WSL2)
1. 主板BIOS开启虚拟化 开启虚拟化需要在BIOS中进行设置,进入主板BIOS→找到虚拟化设置→开启。 2. 检验是否开启虚拟化 打开Windows命令行,并运行 systeminfo固件中已启用虚拟化为是,代表主板BIOS已经开启虚拟化。 3. 启用Windows功能…...
使用Spring的五大类注解读取和存储Bean
目录 1.存储Bean对象的注解 1.1 五大类注解 1.2 方法注解 1.3添加注解的依赖 2.注解的使用 2.1 controller注解 2. 2Service注解 2.3.Resopsitory注解 2.4Component注解 2.5Configuration注解 2.6 注解之间的关系 3.方法注解 3.1 方法注解要配合类注解来使用。 3.2…...

Vue3通透教程【十一】初探TypeScript
文章目录 🌟 写在前面🌟 TypeScript是什么?🌟TypeScript 增加了什么?🌟TypeScript 初体验🌟 写在最后🌟 写在前面 专栏介绍: 凉哥作为 Vue 的忠实 粉丝输出过大量的 Vue 文章,应粉丝要求开始更新 Vue3 的相关技术文章,Vue 框架目前的地位大家应该都晓得,所谓…...
Linux环境安装iperf3(网络性能测试工具)
[rootlocalhost ]# yum search iperf 已加载插件:fastestmirror Loading mirror speeds from cached hostfile* base: mirrors.tuna.tsinghua.edu.cn* extras: mirrors.huaweicloud.com* updates: mirrors.tuna.tsinghua.edu.cnN/S matched: iperf iperf3-devel.i6…...

回顾第一章
回顾 Shell脚本中的$虚函数虚函数和纯虚函数 git merge/rebasegit merge特点git rebase特点 Linux内核调试——coredump获取core dump 深度测试和模板测试2D游戏的制作思路C11特性 Shell脚本中的$ $0: 脚本自身的名称; $1: 传入脚本的第一个参数; $2…...
Jupyter Notebook入门教程
Jupyter Notebook(又称Python Notebook)是一个交互式的笔记本,支持运行超过40种编程语言。本文中我们将介绍Jupyter Notebook的主要特点,了解为什么它能成为人们创造优美的可交互式文档和教育资源的一个强大工具。 首先ÿ…...

独立按键识别
项目文件 文件 关于项目的内容知识点可以见专栏单片机原理及应用 的第四章 IO口编写 参考图电路编写程序,要求实现如下功能: 开始时LED均为熄灭状态,随后根据按键动作点亮相应LED(在按键释放后能继续保持该亮灯状态,直至新的按键压下时为止…...

【论文阅读】AlphaFold2阅读笔记
摘要 给一串氨基酸的序列,去预测他的结构是什么样的 蛋白质的折叠问题 alphaFold精度不够 这里可以达到原子精度的预测 CASP14 精度 这个是什么问题是不是解决了问题 模型的结果并不重要 导论 摘要故事的详细版本 在写论文的时候,可以这样写&a…...

机器学习基础知识之数据归一化
文章目录 归一化的原因1、最大最小归一化2、Z-score标准化3、不同方法的应用 归一化的原因 在进行机器学习训练时,通常一个数据集中包含多个不同的特征,例如在土壤重金属数据集中,每一个样本代表一个采样点,其包含的特征有经度、…...

QCC51XX---pydbg_cmd集合
目录 common pydbg_cmd headset pydbg_cmd earbud pydbg_cmd common pydbg_cmd log apps1.log_level() apps1.fw.gbl.debug_log_level__global 查看log等级apps1.fw.gbl.debug_log_level__global.value = 5 设置log等级 apps1.log()...

camx 马达的MSM_ACTUATOR_WRITE_DAC 操作
camx 马达的MSM_ACTUATOR_WRITE_DAC操作 为什么要分析 MSM_ACTUATOR_WRITE_DACmm-camera MSM_ACTUATOR_WRITE_DACcamx MSM_ACTUATOR_WRITE_DAC总结 为什么要分析 MSM_ACTUATOR_WRITE_DAC 目前的camx源码 省略了hw_mask 的处理。 一般来说 hw_mask 是0 ,但是对于非0…...

【无人机】无人机平台的非移动 GPS 干扰器进行位置估计的多种传感器融合算法的性能分析(Matlab代码实现)
💥 💥 💞 💞 欢迎来到本博客 ❤️ ❤️ 💥 💥 🏆 博主优势: 🌞 🌞 🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 …...
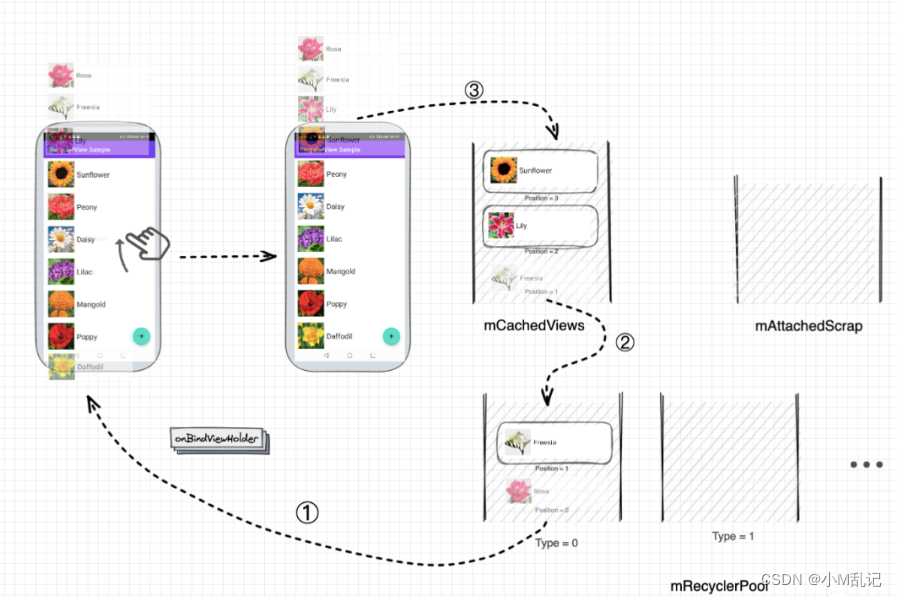
一篇文章搞定《RecyclerView缓存复用机制》
------《RecyclerView缓存复用机制》 前言零、为什么要缓存一、RecyclerView如何构建我们的列表视图二、缓存过程三、缓存结构1、mChangedScrap/mAttachedScrap2、mCachedViews3、mViewCacheExtension4、mRecyclerPool 四、总结 前言 本篇文章,暂时不加入预加载进行…...

Elasticsearch概述
1.Elasticsearch干啥的? Elasticsearch 是一个开源的分布式搜索和分析引擎,用于实时搜索、分析和存储大规模数据。它可以帮助用户在海量数据中快速进行全文搜索、聚合分析、地理空间分析等操作,并支持水平扩展以应对高并发访问需求。 Elasti…...

停车场收费系统
1.系统的开发工具 1.1 AppServe集成应用 Mysql:MySQL 是一款安全、跨平台、高效的,并与 PHP、Java 等主流编程语言紧密结合的数据库系统。该数据库系统是由瑞典的 MySQL AB 公司开发、发布并支持,由 MySQL 的初始开发人员 David Axmark 和 Mi…...
nodejs+vue+elementui学生毕业生离校系统
学生毕业离校系统的开发过程中。该学生毕业离校系统包括管理员、学生和教师。其主要功能包括管理员:首页、个人中心、学生管理、教师管理、离校信息管理、费用结算管理、论文审核管理、管理员管理、留言板管理、系统管理等,前台首页;首页、离…...

儿童用灯哪个品牌好?推荐专业的儿童护眼台灯
一款好的儿童台灯,主要是从5个方面决定,照度及均匀度,蓝光,色温,显指,频闪 ① 照度及均匀度最高是国AA级,其次就是国A级 ② 蓝光一定要选择RG0无危险级,蓝光能量最强,…...

探究Android插件化开发的新思路——Shadow插件化框架
Shadow插件化框架是什么? Shadow是一种Android App的插件化框架,它利用类似于ClassLoader的机制来实现应用程序中的模块化,并让这些模块可以在运行时灵活地进行加载和卸载。Shadow框架主张将一个大型的Android App拆分成多个小模块ÿ…...

SimpleDateFormat和DateTimeFormatter的区别及使用详解
目录 1.简介2.区别3.SimpleDateFormat3.1 字符串转日期3.2 日期转字符串 4.DateTimeFormatter4.1 字符串转日期4.2 日期转字符串 扩展 1.简介 DateTimeFormatter 和 SimpleDateFormat 都是用于格式化日期和时间的类,但是它们有一些区别。 SimpleDateFormat 是 Jav…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
