算法训练营 day46 动态规划 最后一块石头的重量 II 目标和 一和零
算法训练营 day46 动态规划 最后一块石头的重量 II 目标和 一和零
最后一块石头的重量 II
1049. 最后一块石头的重量 II - 力扣(LeetCode)
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
是不是感觉和昨天讲解的416. 分割等和子集非常像了。
本题物品的重量为stones[i],物品的价值也为stones[i]。
对应着01背包里的物品重量weight[i]和 物品价值value[i]。
接下来进行动规五步曲:
- 确定dp数组以及下标的含义
dp[j]表示容量(这里说容量更形象,其实就是重量)为j的背包,最多可以背最大重量为dp[j]。
- 确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题则是:dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
- dp数组如何初始化
因为重量都不会是负数,所以dp[j]都初始化为0就可以了,这样在递归公式dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);中dp[j]才不会初始值所覆盖。
- 确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
- 举例推导dp数组
举例,输入:[2,4,1,1],此时target = (2 + 4 + 1 + 1)/2 = 4 ,dp数组状态图如下:

一维dp数组
class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int a : stones) {sum += a;}int target = sum / 2;int[] dp = new int[target + 1];for (int i =0; i < stones.length; i++) {for (int j = target; j >=stones[i]; j--) {if (j < stones[i]) {dp[j] = dp[j];} else {dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}}return (sum - dp[target]) - dp[target];}
}
二维dp数组
class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int a : stones){sum += a;}int target = sum/2;int[][] dp = new int[stones.length][target+1];for (int j = stones[0]; j <=target; j++) {dp[0][j] = stones[0];}for (int i = 1; i <stones.length; i++) {for (int j = 1; j <=target; j++) {if (j<stones[i]){dp[i][j] = dp[i-1][j];}else {dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-stones[i]]+stones[i]);}}}return (sum - dp[stones.length - 1][target]) - dp[stones.length - 1][target];}
}
目标和
494. 目标和 - 力扣(LeetCode)
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
假设加法的总和为x,那么减法对应的总和就是sum - x。
所以我们要求的是 x - (sum - x) = target
x = (target + sum) / 2
此时问题就转化为,装满容量为x的背包,有几种方法。
这里的x,就是bagSize,也就是我们后面要求的背包容量。
大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。
这么担心就对了,例如sum 是5,S是2的话其实就是无解的
-
确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法
其实也可以使用二维dp数组来求解本题,dp[i][j]:使用 下标为[0, i]的nums[i]能够凑满j(包括j)这么大容量的包,有dp[i][j]种方法。
-
确定递推公式
只要搞到nums[i],凑成dp[j]就有dp[j - nums[i]] 种方法。
凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
-
dp数组如何初始化
从递推公式可以看出,在初始化的时候dp[0] 一定要初始化为1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递推结果将都是0。
-
确定遍历顺序
对于01背包问题一维dp的遍历,nums放在外循环,target在内循环,且内循环倒序。
-
举例推导dp数组
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:

一维dp数组
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int num : nums) {sum += num;}int S = (sum + target) / 2;if (sum < Math.abs(target)) return 0;if ((target + sum) % 2 != 0) return 0;int[] dp = new int[S + 1];dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = S; j >=nums[i]; j--) {dp[j] +=dp[j - nums[i]];}}return dp[S];}
}
二维dp数组
public static int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int num : nums) {sum += num;}int S = (sum + target) / 2;if (sum < Math.abs(target)) return 0;if ((target + sum) % 2 != 0) return 0;int[][] dp = new int[nums.length + 1][S + 1];dp[0][0] = 1;for (int i = 1; i <= nums.length; i++) {for (int j = 0; j <= S; j++) {if (j < nums[i - 1]) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]];}}}return dp[nums.length][S];}
一和零
474. 一和零 - 力扣(LeetCode)
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
本题中strs 数组里的元素就是物品,每个物品都是一个!
而m 和 n相当于是一个背包,两个维度的背包。
-
确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。 -
确定递推公式
dp[i][j]可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。dp[i][j]就可以是dp[i - zeroNum][j - oneNum] + 1。然后我们在遍历的过程中,取
dp[i][j]的最大值。所以递推公式:
dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1); -
dp数组如何初始化
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
-
确定遍历顺序
物品就是strs里的字符串,背包容量就是题目描述中的m和n。
-
举例推导dp数组
以输入:[“10”,“0001”,“111001”,“1”,“0”],m = 3,n = 3为例
最后dp数组的状态如下所示:

public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m + 1][n + 1];for (String str : strs) {int oneNum = 0, zeroNum = 0;for (char c : str.toCharArray()) {if (c == '0') zeroNum++;else oneNum++;}for (int i = m; i >= zeroNum; i--) {for (int j = n; j >= oneNum; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
相关文章:

算法训练营 day46 动态规划 最后一块石头的重量 II 目标和 一和零
算法训练营 day46 动态规划 最后一块石头的重量 II 目标和 一和零 最后一块石头的重量 II 1049. 最后一块石头的重量 II - 力扣(LeetCode) 有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。 每一回合…...
nginx-host绕过实例复现
绕过Nginx Host限制第一种处理方法Nginx在处理Host的时候,会将Host用冒号分割成hostname和port,port部分被丢弃。所以,我们可以设置Host的值为2023.mhz.pw:xxx"example.com,这样就能访问到目标Server块:第二种处理…...

Java学习记录day9
类与对象 内部类 成员内部类 在一个类的内部定义的类。 public class Outer {private int a 10;public void outMethod() {System.out.println("这是外部类中的方法");}// 成员内部类public class Inner{private int b 10;public void innerMethod() {// 外部类…...
ActiveReports.NET 17.0 Crack by Xacker
一个完整的报告解决方案,用于在您的业务应用程序中设计、定制、发布和查看报告。 ActiveReports.NET 通过直观的 Visual Studio 集成报表设计器和丰富的控件帮助您提供精美的报表。ActiveReports 提供基于代码的跨平台报告、易于使用的设计器和灵活的 API。适用于桌…...

【计算机网络】传输层TCP协议
文章目录认识TCP协议TCP协议的格式字段的含义序号与确认号六个标志位窗口大小确认应答(ACK)机制超时重传机制连接管理机制三次握手四次挥手滑动窗口流量控制拥塞控制延迟应答捎带应答面向字节流粘包问题TCP异常情况总结认识TCP协议 传输控制协议 (TCP,T…...
Mysql5.7安装【Windows版】
文章目录一、下载二、添加到环境变量三、添加配置文件my.ini四、安装Mysql 修改密码一、下载 下载地址 滑倒最下面有一个MySQL Community Server 选择要下载的版本 二、添加到环境变量 下载好了之后开始解压 把bin目录添加到环境变量 可以点击进入bin目录,直接复…...
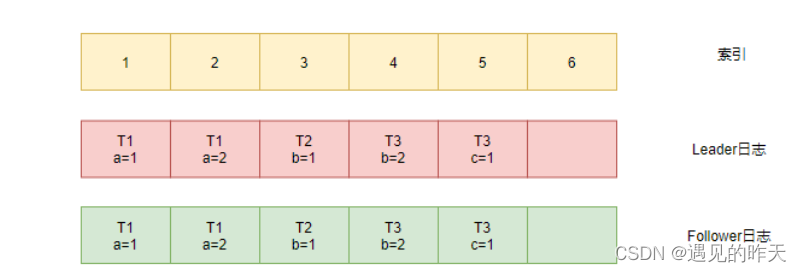
分布式一致性算法Raft原理图释
什么是分布式一致性算法Raft 分布式一致性算法Raft:指在分布式场景下实现集群数据同步的解决方案 掌握了这个算法,就可以较容易地处理绝大部分场景的容错和数据一致性需求 Raft三大角色 跟随者(Follower):普通群众…...
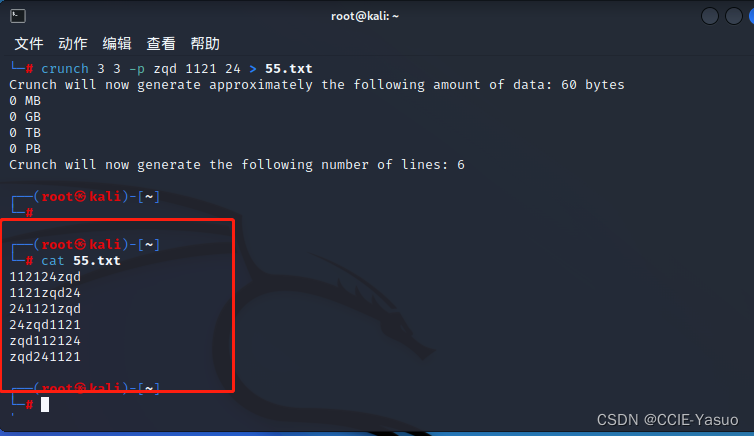
网络安全-字典生成-crunch
网络安全-字典生成-crunch crunch工具,在kali已经集成好了 2是代表最小字符长度 4是最大字符长度 生成了一个2M的文件 还有我们来查看这个密码本 从abcd26个英文字母的2位到4位的组合,他全部排列了一次 还可以自定义数字,特殊字符…...

闪光桐人の实习日记
2023年2月13日 1,认识了职场礼仪,学习了职场礼仪的重要性 尊重->心情愉悦->建立信任与好感->合作机遇的敲门砖 2,学习了职场礼仪中的邮件礼仪 模板管理中设置自己的名片 部门写到三级部,如果部门名太长要换一行 发送…...

PostgreSQL 常见配置参数
max_wal_size : 两个检查点(checkpoint)之间,WAL可增长的最大大小,即:自动WAL checkpoint允许WAL增长的最大值。该值缺省是1GB。如果提高该参数值会提升性能,但也是会消耗更多空间、同时会延长崩溃恢复所需…...

JAVA 常用类型之String结构
String在java中我们是用来操作字符串的,但它的底层结构确是一个char[]数组,通过数组的方式将每个字符进行保存。 使用时:String str"ABCD",内部存value确是:value[A,B,C,D]; 如下图: 参考String源…...

二三层网络设备封装与解封装原理
1、寻址转发(寻址指的是寻找IP地址) 路由表放在一个公共的地方,比如主控板上,由主控板 的CPU运行路由协议,计算路由,生成和维护路由表。 转发表与路由表: 转发表是根据路由表生成的。路由表中…...

9、MyBatis框架——使用注解开发实现数据库增删改查操作、一级缓存、二级缓存、MyBatis实现分页
目录 一、使用注解开发实现数据库增删改查操作 1、搭建项目 2、使用注解开发操作数据库 二、一级缓存 1、一级缓存失效的情况 三、二级缓存 1、手动开启二级缓存cacheEnabled 2、二级缓存机制 四、MyBatis实现分页 1、配置环境 2、startPage()开启分页 3、PageInfo…...

C++STL剖析(六)—— set和multiset的概念和使用
文章目录🌟 前言🍑 树型结构和哈希结构🍑 键值对1. set的介绍和使用🍑 set的模板参数列表🍑 set的构造🍑 set的使用🍅 insert🍅 find🍅 erase🍅 swap…...
SpringColud第四讲 Nacos的Windows安装方式和Linux的安装方式
在Nacos的GitHub页面,提供有下载链接,可以下载编译好的Nacos服务端或者源代码: 目录 1.Windows安装Nacos 1.1.下载 1.2.解压 1.3.修改相关配置: 1.4.启动: 1.5.登录: 2.Linux的安装方式Nacos 2.1.…...
微服务项目【网关服务限流熔断降级分布式事务】
网关服务限流熔断降级 第1步:启动sentinel-dashboard控制台和Nacos注册中心服务 第2步:在网关服务中引入sentinel依赖 <!-- sentinel --> <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-…...

【情人节用Compose给女神写个爱心动画APP】
情人节用Compose给女神写个爱心动画APP前言涉及知识点实现思路实现过程绘制爱心创建动画效果Preview预览效果完整源码彩蛋前言 前一阵子看电视里的学霸用代码写了个炫酷的爱心,网上有很多js和python的源码,复制粘贴就能拥有,但是Android的好…...
GUI swing和awt
GUI(Graphical User Interface,简称 GUI,图形用户界面)是指采用图形方式显示的计算机操作用户界面,与早期计算机使用的命令行界面相比,图形界面对于用户来说在视觉上更易于接受。Java GUI主要有两个核心库&…...
速通Spring
尚硅谷2023最新版Spring6课程_bilibili 1 Spring 【强制】Spring是什么? 1) Spring是一款主流的Java EE轻量级开源框架。 轻量级:体积很小,且不需要依赖于其他组件。 2) 狭义的Spring。 Spring Framework。 3) 广义的Spring。 以Spring F…...
【C++】C++入门
一、 C关键字(C98) C有63个关键字(C语言有32个),如下: asmdoifreturntrycontinueautodoubleinlineshorttypedefforbooldynamic_castintsignedtypeidpublicbreakelselongsizeoftypenamethrowcaseenummutabl…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
