OSQP二次规划求解库使用说明
OSQP二次规划求解库使用说明
贺志国
2023.5.10
1. 凸二次规划的一般表达式
m i n 1 2 x T P x + q T x s . t . l ≤ A x ≤ u min \quad \frac{1}{2}x^T Px + q^Tx \qquad s.t. \quad l \leq Ax \leq u min21xTPx+qTxs.t.l≤Ax≤u
其中, P P P称为内核矩阵,要求是半正定矩阵。正定矩阵在复数域上是共轭对称矩阵(Hermite矩阵),在实数域上是对称矩阵。因为我们在实数域内求解, P P P也是一个对称矩阵。 q q q称为偏移向量, A A A称为仿射矩阵。
凸二次规划的求解算法主要有如下几种:
- 有效集法:Active Set Method
- 内点法:Interior Point Method
- 一阶方法:First Order Method
- 交替方向乘子法:Alternating Direction Method of Multipliers(ADMM)
OSQP利用交替方向乘子法(ADMM)求解,qpOASES则利用有效集法,从网上给出的测评报告看,OSQP库的求解效率比qpOASES库要高很多。
2. 使用OSQP求解凸二次规划的简单示例
为了形象地说明使用OSQP求解凸二次规划的过程,下面给出一个简单的示例:
m i n 1 2 x T [ 4 1 1 2 ] x + [ 1 1 ] T x min \quad \frac{1}{2}x^T\left[\begin{matrix} 4 & 1\\ 1 & 2\end{matrix}\right]x + \left[\begin{matrix} 1 \\ 1\end{matrix}\right]^Tx min21xT[4112]x+[11]Tx
s.t. (subject to):
[ 1 0 0 ] ≤ [ 1 1 1 0 0 1 ] x ≤ [ 1 0.7 0.7 ] \left[\begin{matrix}1 \\ 0 \\ 0 \end{matrix}\right] \leq \left[\begin{matrix} 1 & 1 \\ 1 & 0 \\ 0 & 1 \end{matrix}\right]x \leq \left[\begin{matrix}1 \\ 0.7 \\ 0.7 \end{matrix}\right] 100 ≤ 110101 x≤ 10.70.7
本示例中,内核矩阵 P = [ 4 1 1 2 ] P=\left[\begin{matrix} 4 & 1\\1 & 2\end{matrix}\right] P=[4112]的元素全部为实数,因此它一定是对称矩阵。对于对称矩阵,只需要存储上三角矩阵即可,这也是OSQP存储稀疏矩阵的常见做法,当然也是该库提高计算效率的有效措施。
具体而言,OSQP库使用csc_matrix(indices, indptr, data, csc = Compressed Sparse Column)的方式来存储一个矩阵。csc_matrix存储格式定义如下:
- indices is array of row indices
- data is array of corresponding nonzero values
- indptr points to column starts in indices and data
下面仍然以内核矩阵 P = [ 4 1 1 2 ] P=\left[\begin{matrix} 4 & 1\\1 & 2\end{matrix}\right] P=[4112]为例进行说明。首先,将内核矩阵简化为上三角矩阵:
P = [ 4 1 0 2 ] P=\left[\begin{matrix} 4 & 1\\0 & 2\end{matrix}\right] P=[4012]
P P P的非零元素个数为3,记为:P_nnz = 3 (nnz: number of non-zero elements)
P P P中非零元素为:4, 1, 2,记为:P_x = {4, 1, 2};
P P P中非零元素行索引为:0, 0, 1,这是按照先第一列,再第二列。。。,最后第N列的顺序标记。第一列的非零元素是4,行索引为0;第二列的非零元素为1, 2,行索引分别为:0, 1,于是记为:P_i = {0, 0, 1};
P P P中第一列非零元素是1个,第二列非零元素是2个,记为:P_p = {0, 1, 3}。这个记法有些反人类,也很难形象理解,容我再详细解释一番。P_p元素个数为矩阵列数加1,P_p的第一个元素为0,P_p中前后两个元素的差值表示矩阵P相应列的非零元素个数。例如:P_p = {0, 1, 3}表示:1 - 0 = 1 代表矩阵P第一列元素非零个数为1个,3 - 1 = 2 代表矩阵P第二列元素非零个数为2个。助记方法:P_i (i代表indices), P_p(p代表indptr)。
根据上述介绍,下面给出该示例的求解代码:
#include "osqp.h"int main(int argc, char **argv) {// P矩阵是对称矩阵,只存储上三角部分,下三角部分视为零值c_float P_x[3] = {4.0, 1.0, 2.0, }; // P矩阵非零元素个数为3// nnz = number of non-zero elements.c_int P_nnz = 3; // P矩阵非零元素行索引,按照先第一列,再第二列。。。// 的顺序排列。下例表示非零元素的行序号为0、0、1c_int P_i[3] = {0, 0, 1, }; // 1-0=1表示第0列非零元素个数// 3-1=2表示第1列非零元素个数c_int P_p[3] = {0, 1, 3, }; c_float q[2] = {1.0, 1.0, };// A矩阵非零元素c_float A_x[4] = {1.0, 1.0, 1.0, 1.0, };// A矩阵非零元素个数为4c_int A_nnz = 4;// A矩阵非零元素的行序号为0、1、0、2(按列排序)c_int A_i[4] = {0, 1, 0, 2, };// 2-0=2表示第0列2个元素非零// 4-2=2表示第1列2个元素非零c_int A_p[3] = {0, 2, 4, };c_float l[3] = {1.0, 0.0, 0.0, };c_float u[3] = {1.0, 0.7, 0.7, };c_int n = 2;c_int m = 3;// Exitflagc_int exitflag = 0;// Workspace structuresOSQPWorkspace *work;OSQPSettings *settings = (OSQPSettings *)c_malloc(sizeof(OSQPSettings));OSQPData *data = (OSQPData *)c_malloc(sizeof(OSQPData));// Populate dataif (data) {data->n = n;data->m = m;data->P = csc_matrix(data->n, data->n, P_nnz, P_x, P_i, P_p);data->q = q;data->A = csc_matrix(data->m, data->n, A_nnz, A_x, A_i, A_p);data->l = l;data->u = u;}// Define solver settings as defaultif (settings) {osqp_set_default_settings(settings);settings->alpha = 1.0; // Change alpha parameter}// Setup workspaceexitflag = osqp_setup(&work, data, settings);// Solve Problemosqp_solve(work);// Cleanupif (data) {if (data->A) c_free(data->A);if (data->P) c_free(data->P);c_free(data);}if (settings) c_free(settings);return exitflag;
}
相关文章:

OSQP二次规划求解库使用说明
OSQP二次规划求解库使用说明 贺志国 2023.5.10 1. 凸二次规划的一般表达式 m i n 1 2 x T P x q T x s . t . l ≤ A x ≤ u min \quad \frac{1}{2}x^T Px q^Tx \qquad s.t. \quad l \leq Ax \leq u min21xTPxqTxs.t.l≤Ax≤u 其中, P P P称为内核矩阵&#x…...

Elasticsearch(一)
Elasticsearch(一) 初始elasticsearch 什么是elasticsearch elasticsearch是一款非常强大的开源搜索引擎,可以帮助我们从海量数据中快速查找到需要的内容 elasticsearch结合kibana、Logstash、Beats,也就是elastic stack&…...

深入探究Java中的枚举类型:定义、特性和应用
引言: 在Java编程中,枚举类型是一种强大而灵活的工具,用于定义一组具名的常量。它不仅提供了代码可读性和可维护性的优势,还为开发人员提供了一种更安全和结构化的方式来处理固定的常量集合。本文将深入探讨Java中的枚举类型&…...

linux密码忘了?一招解决
目录 一、前言 二、进入编辑界面 三、单用户模式 四、修改密码 五、更新信息 六、退出 七、验证 一、前言 版本:centos7.9、VMware15.5 在我们学习linux运行级别的时候,面试题可能会出如何找回root密码,下面来详细的介绍一波ÿ…...
苹果mac清理软件CleanMyMac X v4.13兼容13系统,堪称Mac最好的系统清理工具
CleanMyMac X for mac是MacOS上一款Mac清理优化工具,不仅包含各种清理功能,更是具有卸载器、维护、扩展、碎纸机这些实用功能,可以同时代替很多工具。它可以清理,优化,保养和监测您的电脑,确保您的Mac运行…...
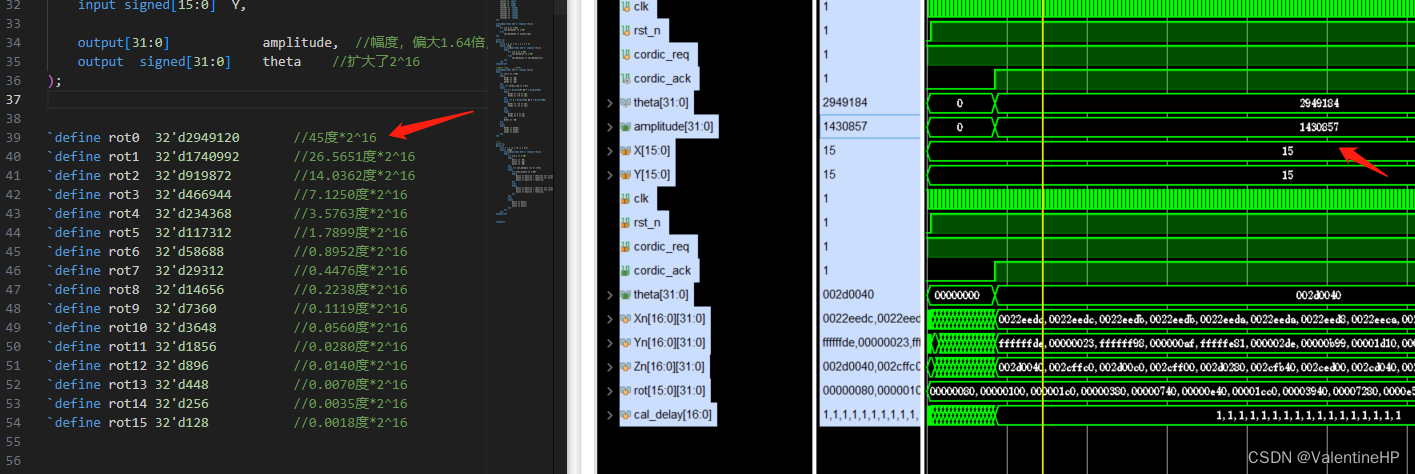
FPGA实现Cordic算法求解arctan和sqr(x*2 + y* 2)
一. 简介 由于在项目中需要使用的MPU6050,进行姿态解算,计算中设计到**arctan 和 sqr(x2 y 2),**这两部分的计算,在了解了一番之后,发现Cordic算法可以很方便的一次性求出这两个这两部分的计算。另外也可以一次性求出sin和cos的…...

【最终截稿 | Springer 独立出版 | EI稳定检索】 2023年绿色建筑国际会议(ICoGB 2023)
会议简介 Brief Introduction 2023年绿色建筑国际会议(ICoGB 2023) 会议时间:2023年5月21日-23日 召开地点:瑞典斯德哥尔摩 大会官网:www.icogb.org ICoGB 2023将围绕“绿色建筑”的最新研究领域而展开,为研究人员、工程师、专家学…...

Flutter常用状态管理框架及优缺点
Flutter 中常见的状态管理框架有以下几种: Provider: Provider 是一个轻量级的状态管理框架,可用于单个 Widget 或整个 Widget 树中分发状态。它通过 InheritedWidget 和 ChangeNotifier 来实现状态管理,并支持依赖项注入。Redux…...
Ubuntu 20.04 系统配置 OpenVINO 2022.3 环境
由于 OpenVINO 2021 版本在调用 IECore 时会出现 Segmentation fault 的问题,因此需要将其升级为 2022 版本的。 1. 卸载原来版本的 OpenVINO 进入OpenVINO的卸载目录,通常在 /opt/intel 文件夹下, cd /opt/intel/openvino_2021/openvino_…...

浏览器存储技术:localStorage、sessionStorage和cookie的区别
随着互联网技术的不断发展,人们越来越依赖浏览器进行网页浏览和数据处理。浏览器存储技术是Web开发中非常重要的一部分,它可以帮助我们在浏览器端存储数据,而无需将数据传输到服务器。本文将介绍三种常见的浏览器存储技术:localSt…...

MySQL中的内连接和外连接
一、MySQL内连接(INNER JOIN) 内连接,又称为等值连接,是最常见的连接类型。它根据两个(或多个)表中具有相同列值的行来创建一个新的结果表。在内连接中,只有通过连接条件匹配的行才会被包含在结…...

node学习手册
Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行时,使 JavaScript 可以脱离浏览器环境运行在服务端。它提供了一组 API,可以让开发者轻松地进行服务器端编程。 以下是 Node.js 的学习手册: 安装 Node.js 首先,需要在官网…...

Java中的JSP是什么?如何实现JSP
JavaServer Pages(JSP)是一种Java技术,可以用于开发动态Web应用程序。它允许开发人员将Java代码嵌入到HTML页面中,以便生成动态内容。本文将介绍JSP的工作原理,以及如何在Java中实现JSP。 JSP的工作原理 JSP的工作原…...
c++之函数对象和谓词
目录 函数对象: 谓词: 一元谓词函数举例如下 二元谓词举例如下 函数对象和函数的区别 一元谓词的案例 二元函数对象案例 二元谓词案例 函数对象: 重载函数调用操作符的类,其对象常称为函数对象(function obj…...
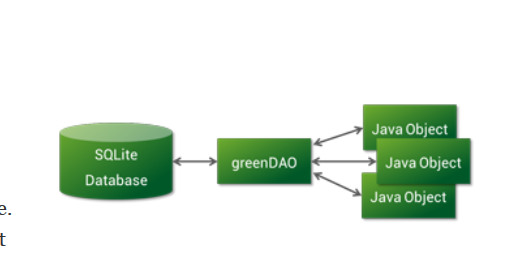
《Andorid开源》greenDao 数据库orm框架
一 前言:以前没用框架写Andorid的Sqlite的时候就是用SQLiteDatabase ,SQLiteOpenHelper ,SQL语句等一些东西,特别在写SQL语句来进行 数据库操作的时候是一件很繁琐的事情,有时候没有错误提示的,很难找到错误的地方&a…...
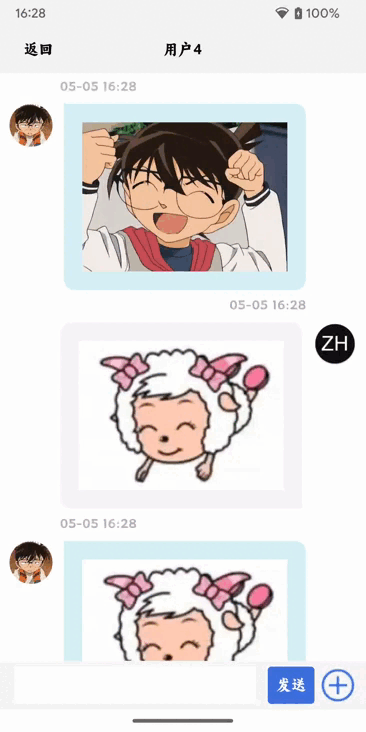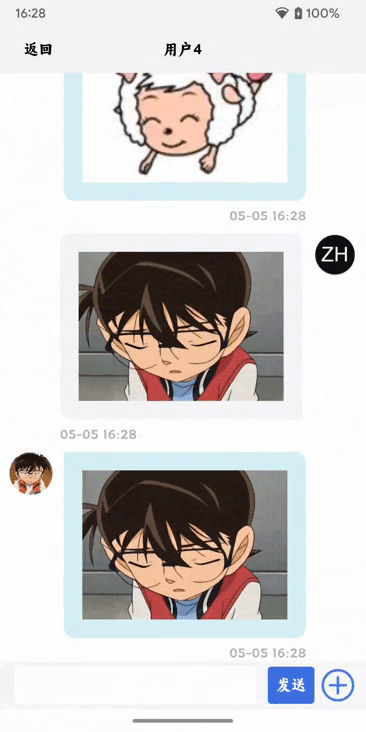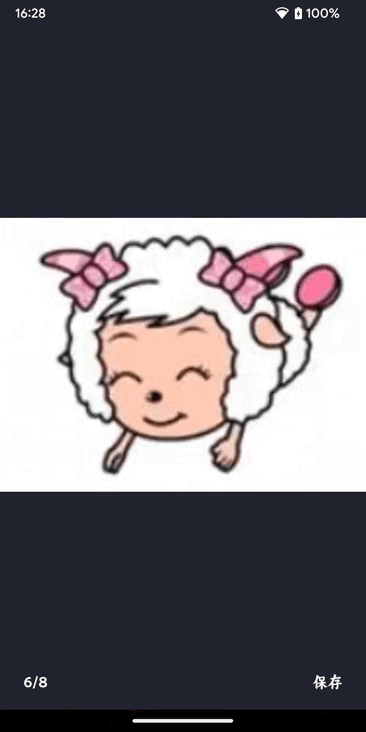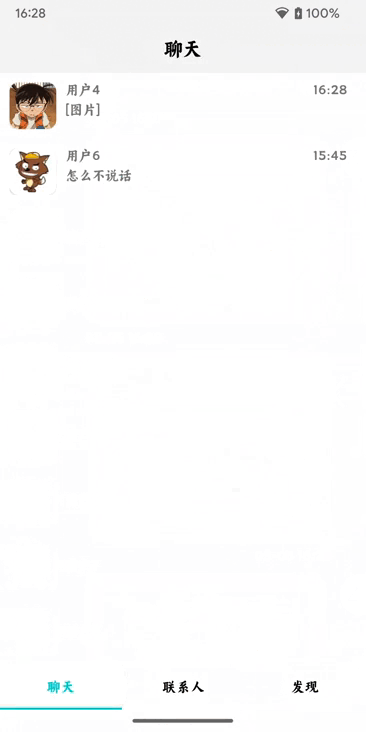
Android类似微信聊天页面教程(Kotlin)五——选择发送图片
前提条件 安装并配置好Android Studio Android Studio Electric Eel | 2022.1.1 Patch 2 Build #AI-221.6008.13.2211.9619390, built on February 17, 2023 Runtime version: 11.0.150-b2043.56-9505619 amd64 VM: OpenJDK 64-Bit Server VM by JetBrains s.r.o. Windows 11 …...

MongoDB:Win/Linux环境安装及一键部署脚本
1. Win安装 1.1 下载 MongoDB 安装程序 访问 MongoDB 官网,进入下载页面:Download MongoDB Community Server | MongoDB 选择 Windows 平台并下载最新版的 MongoDB 安装程序。 1.2 安装 MongoDB 双击安装程序,按照提示完成 MongoDB 的安装…...

KingbaseES V8R3 集群运维系列 -- failover切换后集群自动恢复
案例说明: KingbaseES V8R3集群默认在触发failover切换后,为保证数据安全,原主库需要通过人工介入后,恢复为新的备库加入到集群。在无人值守的现场环境,需要在触发failover切换后,主库可以自动恢复为新备…...
【Selenium中】——全栈开发——如桃花来
目录索引 查找元素:查找方法:单个元素查找:多个元素查找:*代码演示:* 元素交互操作:清空文字: 推荐的变量名定义名称:执行JavaScript :滚动页面方法:*滚动到底…...

Sarsa增强版之Sarsa-λ依然走迷宫
Sarsa-λ(Sarsa Lambda)是Sarsa算法的一种变体,其中“λ”表示一个介于0和1之间的参数,用于平衡当前状态和之前所有状态的重要性。 Sarsa算法是一种基于Q-learning算法的增量式学习方法,通过在实际环境中不断探索和学…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
