递归到动态规划:省去枚举行为
如果在动态规划的过程中没有枚举行为,那严格位置依赖和傻缓存的方式并没有太大区别,但是当有枚举行为的时候(一个位置依赖于多个位置),那严格位置依赖是有优化空间的,枚举行为也许可以省去,题目:
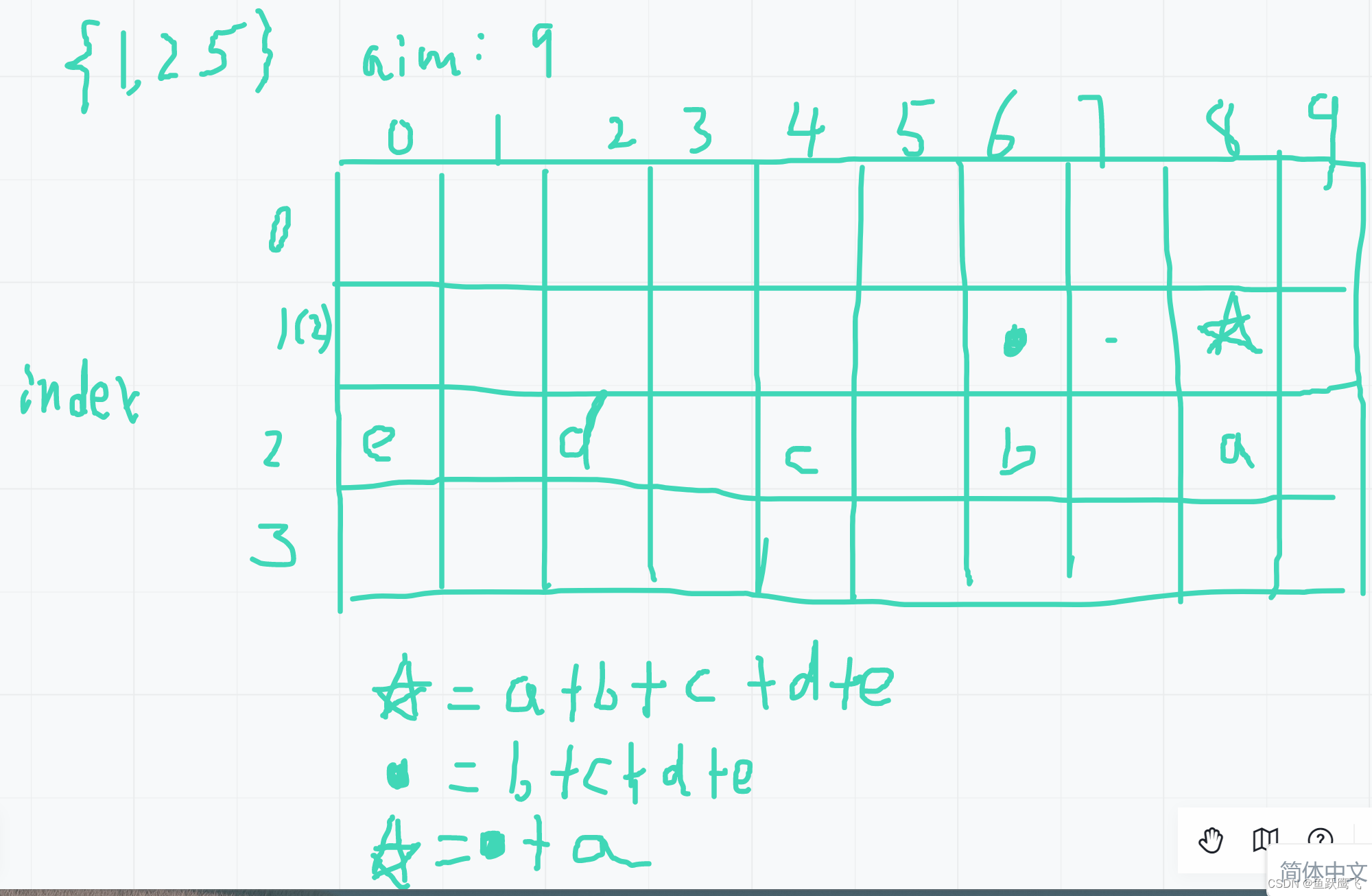
| arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。 每个值都认为是一种面值,且认为张数是无限的。 返回组成aim的方法数 例如:arr = {1,2},aim = 4 方法如下:1+1+1+1、1+1+2、2+2 一共就3种方法,所以返回3 |
这个题目的动态规划普遍位置({1,8})的依赖,我们原来dp[1][8] = dp [2][8] + dp[2][6] + dp[2][4] + dp[2][2] + dp[2][0]
而dp[1][6] = dp[2][6] + dp[2][4] + dp[2][2] + dp[2][0]
我们可以看到计算dp[2][8]时候用到的 dp[2][6] + dp[2][4] + dp[2][2] + dp[2][0]之前其实是计算过的,这个值就是dp[1][6]
所以可以简化为dp[1][6] + dp[2][8]
普遍位置就是dp[index][rest] = dp[index+1][rest] + dp[index][rest-arr[index]]
dp[index][rest-arr[index]]这个要先判断存在不存在
也就是它依赖于它的下方和左边,dp数组按照从下到上,从左到右的顺序初始化即可
对应的代码如下:
package dataStructure.recurrence.practice;/*** arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。* 每个值都认为是一种面值,且认为张数是无限的。* 返回组成aim的方法数* 例如:arr = {1,2},aim = 4* 方法如下:1+1+1+1、1+1+2、2+2* 一共就3种方法,所以返回3*/
public class CoinsWayNoLimit {public static int coinsWay(int[] arr, int aim) {return process1(arr, 0, aim);}/*** 动态规划的解法-原始版* 根据递归,可变的参数是index和rest,变化范围分别是0~arr.length, 0~rest* @param arr 原始的数组* @param aim 要组成的目标* @return*/public static int coinsWayDp(int[] arr, int aim) {int[][] dp = new int[arr.length + 1][aim + 1];//最后一行只有0位置是1,其他都是0(0是int默认值,不需要初始化)dp[arr.length][0] = 1;//根据递归,所有的(index, rest)都依赖于下一行前面的某个位置//所以行必须从下往上,列初始化的顺序无所谓for(int index = arr.length - 1; index >=0; index --) {for(int rest = 0; rest <= aim; rest ++) {int ways = 0;for(int num = 0; num * arr[index] <= rest; num ++) {ways += dp[index + 1][rest - (num * arr[index])];}dp[index][rest] = ways;}}return dp[0][aim];}/*** 动态规划的解法-原始版* 根据递归,可变的参数是index和rest,变化范围分别是0~arr.length, 0~rest* @param arr 原始的数组* @param aim 要组成的目标* @return*/public static int coinsWayDpBest(int[] arr, int aim) {int[][] dp = new int[arr.length + 1][aim + 1];//最后一行只有aim位置是1,其他都是0(0是int默认值,不需要初始化)dp[arr.length][0] = 1;//根据递归,所有的(index, rest)都依赖于下一行前面的某个位置//所以行必须从下往上,这里我们要省掉枚举行为,一个位置依赖于他下面的位置和他前面的某个位置,所以必须从前往后for(int index = arr.length - 1; index >=0; index --) {for(int rest = 0; rest <= aim; rest ++) {//这是倒数第二行,他下面肯定有位置dp[index][rest] = dp[index + 1][rest];//但是左边的位置rest-arr[index]不一定存在,所以要做判断if(rest-arr[index] >= 0) {//如果存在就加上dp[index][rest] += dp[index][rest-arr[index]];}}}return dp[0][aim];}/*** 递归黑盒方法,从index号下标开始组成left* @param arr 原始的面值数组,每个面值都是无限的* @param index 当前要考虑的位置下标* @param rest 还差多少钱* @return*/public static int process1(int[] arr, int index, int rest) {if(rest < 0) return 0;if(index == arr.length) {return rest == 0? 1 : 0;}int ways = 0;for(int num = 0; num * arr[index] <= rest; num++) {ways += process1(arr, index + 1, rest - (num * arr[index]));}return ways;}public static void main(String[] args) {int[] arr = {1,2};int aim = 4;int ways = coinsWay(arr, aim);System.out.println(ways);int waysDp1 = coinsWayDp(arr, aim);System.out.println(waysDp1);int waysDpBest = coinsWayDpBest(arr, aim);System.out.println(waysDpBest);}
}
省去了枚举行为,结果完全一致,原来的时间复杂度是O(N * M * K),现在的话变成了O(N * M)
其中K是rest/数组中最小的那个面值
个人的总结是:如果某个位置只依赖它的90度角范围内的枚举都是可以优化的(上、左 上、左上、左 等等)
欢迎私信讨论
相关文章:

递归到动态规划:省去枚举行为
如果在动态规划的过程中没有枚举行为,那严格位置依赖和傻缓存的方式并没有太大区别,但是当有枚举行为的时候(一个位置依赖于多个位置),那严格位置依赖是有优化空间的,枚举行为也许可以省去,题目…...

服务(第二十一篇)mysql高级查询语句(二)
①视图表: 视图表是虚拟表,用来存储SQL语句的定义 如果视图表和原表的字段相同,是可以进行数据修改的; 如果两者的字段不通,不可以修改数据。 语法: 创建:create view 试图表名 as ... 查…...

MYSQL高可用配置(MHA)
1、什么是MHA MHA(Master High Availability)是一套优秀的MySQL高可用环境下故障切换和主从复制的软件。 MHA 的出现就是解决MySQL 单点的问题。 MySQL故障切换过程中,MHA能做到0-30秒内自动完成故障切换操作。 MHA能在故障切换的过程中最大…...

单精度浮点数与十进制数据相互转换
一、float基础: Float类型占4个字节,也就是32bit,其中最高位是符号位,2~9位是指数位,后边的23bit是数值位.如下所示 大部分数据的二进制形式都可以用科学计数法表示,即1.m*2^n这种形式,只要知道m和n,就能确定一个数值 二、小数位如何转变为二进制: 下面…...

PMP敏捷-4大价值观、12原则
宣言及4大价值观 个体及互动 胜于 流程和工具 以人为本 工作的软件 胜于 完整的文档 以价值为导向 客户合作 胜于 合同谈判 合作共赢 应对变更 胜于 遵循计划 拥抱变化 12原则 工作原则:精益、至简,实现这种原则的方式是“定期反省”。9、10、12 …...
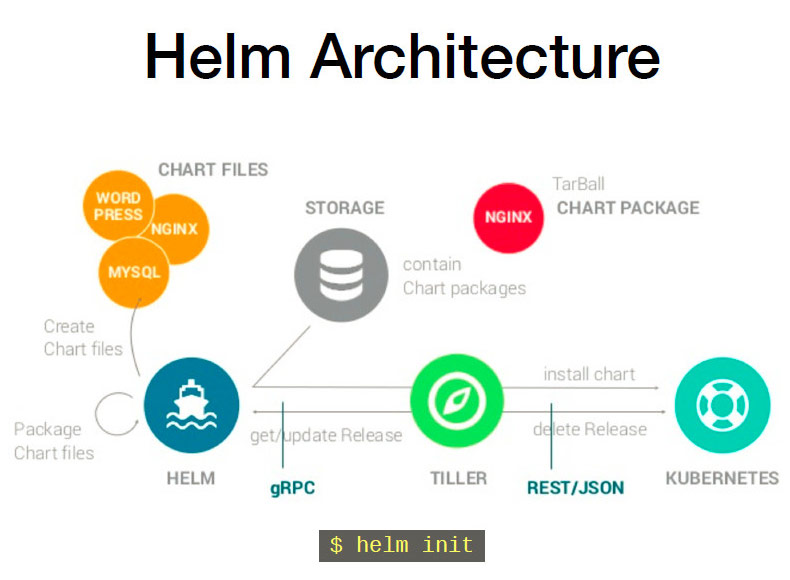
K8S—Helm
一、Helm介绍 helm通过打包的方式,支持发布的版本管理和控制,很大程度上简化了Kubernetes应用的部署和管理。 Helm本质就是让k8s的应用管理(Deployment、Service等)可配置,能动态生成。通过动态生成K8S资源清单文件&a…...

ALSA内部函数调用流程
ALSA内部函数调用流程 一直都有这样的一个疑问 就是在linux系统中我们调用snd_pcm_open后,就不知道alsa内部是怎么运行的了 用户的pcm_open()相当于先对ASoC各个驱动模块startup(),再做hw_params()。 pcm_open()pcm->fd open("/dev/snd/pcm…...

Python正则表达式详解,保姆式教学,0基础也能掌握正则
正则作为处理字符串的一个实用工具,在Python中经常会用到,比如爬虫爬取数据时常用正则来检索字符串等等。正则表达式已经内嵌在Python中,通过导入re模块就可以使用,作为刚学Python的新手大多数都听说”正则“这个术语。 今天来给…...

ChatGPT 接入飞书教程,创建自己的聊天机器人
ChatGPT 接入飞书教程,创建自己的聊天机器人 一、飞书进入开发者平台。点击创建应用。二、打开Aircode,点击创建应用,上面输入名字,下面选择Node.js v16三、配置环境,点击Environments,创建四个变量,全部要大写本教程收集于: AIGC从入门到精通教程 首先,准备三个账号…...
)
JS生成随机数(多种解决方案)
JS生成随机数 概述 随机数是编程语言中的重要组成部分。在JavaScript中,生成随机数是一项简单的任务。本文将介绍生成随机数的各种方法。 Math.random() Math.random()是JavaScript中生成随机数最常见的方法。该方法返回介于0和1之间的随机数。例如,…...

文件IO 函数 静态库和动态库的创建 5.11
5.11 文件IO函数 1.数据读写 ssize_t read(int fd,void *buf,size_t count); 功能: 从fd对应的文件中 读取前count个字节的数据到buf缓冲区中 头文件: #include <unistd.h> 参数: fd :文件描述符 buf…...

考研日语-详解ている、てある、ていく、てくる用法
目录 一、ている用法 1. 表示现在状态 2. 表示持续动作 3. 表示经验或习惯 4. 表示结果或效果 二、てある用法 1. 表示已经完成的动作 2. 表示现在状态 3. 表示被动 三、ていく用法 1. 表示未来的动作 2. 表示逐渐变化的过程 四、てくる用法 1. 表示过去到现在的…...

Spring Security 6.x 系列【36】授权服务器篇之OpenID Connect 1.0
有道无术,术尚可求,有术无道,止于术。 本系列Spring Boot 版本 3.0.4 本系列Spring Security 版本 6.0.2 本系列Spring Authorization Server 版本 1.0.2 源码地址:https://gitee.com/pearl-organization/study-spring-security-demo 文章目录 1. 前言2. OpenID Connect…...
【计算机视觉 | Pytorch】timm 包的具体介绍和图像分类案例(含源代码)
一、具体介绍 timm 是一个 PyTorch 原生实现的计算机视觉模型库。它提供了预训练模型和各种网络组件,可以用于各种计算机视觉任务,例如图像分类、物体检测、语义分割等等。 timm 的特点如下: PyTorch 原生实现:timm 的实现方式…...

轻博客Plume的搭建
什么是 Plume ? Plume 是一个基于 ActivityPub 的联合博客引擎。它是用 Rust 编写的,带有 Rocket 框架,以及 Diesel 与数据库交互。前端使用 Ructe模板、WASM 和SCSS。 反向代理 假设我们实际访问地址为: https://plume.laosu.ml…...

机器人关节电机PWM
脉冲宽度调制(Pulse width modulation,PWM)技术。一种模拟控制方式 机器人关节电机的控制通常使用PWM(脉冲宽度调制)技术。PWM是一种用于控制电子设备的技术,通过控制高电平和低电平之间的时间比例,实现对电子设备的控制。在机器人关节电机中,PWM信号可以控制电机的…...

MPU6050详解(含源码)
前言:MPU6050是一款强大的六轴传感器,需要理解MPU6050首先得有IIC的基础,MPU6050 内部整合了 3 轴陀螺仪和 3 轴加速度传感器,并且含有一个第二 IIC 接口,可用于连接外部磁力传感器,内部有硬件算法支持. 1…...

Vue入门学习笔记:TodoList(三):实例中的数据、事件和方法
目录: Vue入门学习笔记:TodoList(一):HelloWorld Vue入门学习笔记:TodoList(二):挂载点、模板、实例 Vue入门学习笔记:TodoList(三)&a…...

怎么找到引发回流的JavaScript代码?
要找到引发回流的JavaScript代码,可以使用浏览器的开发者工具中的性能分析器。不同的浏览器有不同的名称和位置,例如Google Chrome的开发者工具中的性能分析器被称为Performance,Firefox的开发者工具中的性能分析器被称为Profiler。 以下是在…...

未来广告策划,转型还是淘汰?
在广告行业呆了十来年了,最近我越来越感觉到广告行业真的是一个需要与时俱进,并且应用场景非常广泛的一个专业。 而且由于这是一个需要创意能力的行业,所以对比于重复性容易被机器以及人工智能所代替的岗位行业来说,广告的可替代…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
