【C++】AVL树

 

---

目录

 1 简介

2 实现

2.1 框架构建

2.2 插入操作

2.2.1 平衡因子的更新

2.2.2 平衡因子异常时树的调整

3 检验 

---

 1 简介

AVL树基于二叉搜索树之上，又对其提出了平衡的要求，即：当向二叉搜索树插入新节点后，保证每个节点的左右子树高度之差的绝对值不超过1

AVL树具有如下性质：

1、它的左右子树都是二叉搜索树。

2、左右子树高度之差（简称平衡因子 = 右子树高度 - 左子树高度）的绝对值不超过1。

AVL树有多种方法来实现，使用平衡因子的方式只是其中一种，接下来讲解实现过程。

2 实现

2.1 框架构建

#pragma once
#include<iostream>template<class K, class V>
struct AVLTreeNode
{std::pair<K, V> _kv;AVLTreeNode<K, V>* _left; //左指针AVLTreeNode<K, V>* _right; //右指针AVLTreeNode<K, V>* _parent; //父指针int _bf; //balance factor 平衡因子
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public://
private:Node* _root = nullptr;
};

2.2 插入操作

2.2.1 平衡因子的更新

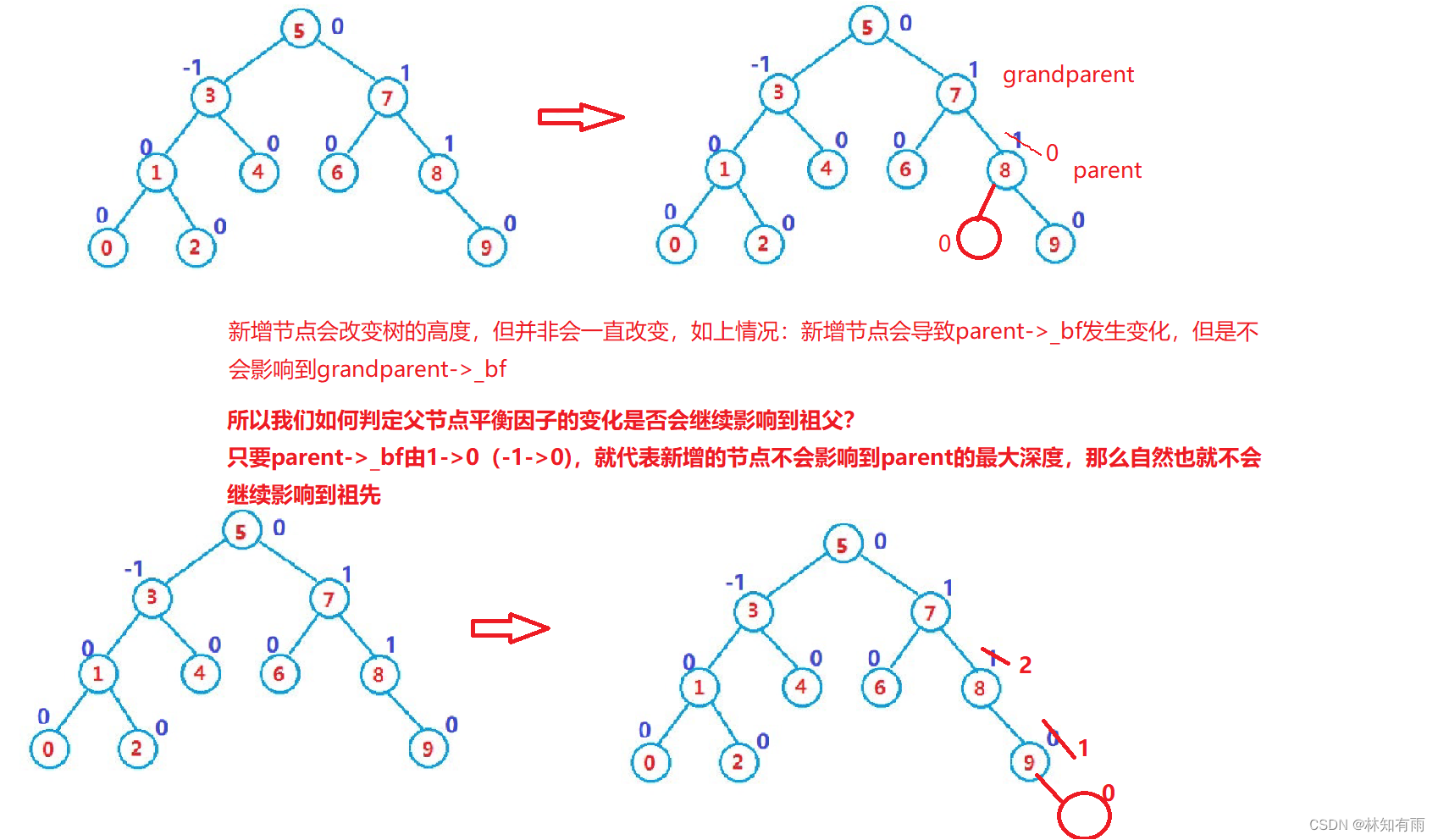
//1、更新平衡因子转换成代码
//这里注意：最坏情况下，平衡因子要持续更新到根节点后停止while (parent){if (cur == parent->_left)--parent->_bf;else++parent->_bf;if (parent->_bf == 0)break;else if(parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if(parent->_bf == 2 || parent->_bf == -2){//调整树来减小平衡因子}else assert(false);}

2.2.2 平衡因子异常时树的调整

对于如何调整树，我们引入AVL树的旋转操作，AVL树的旋转分为4种

而旋转最终的目的：

1、让这颗子树左右高度差不超过1

2、旋转过程中让它继续保持是搜索树

3、更新调整孩子节点的平衡因子

4、让这棵树的高度跟插入前保持一致

情况1：新节点插入较深右子树的右侧---右右：左单旋 

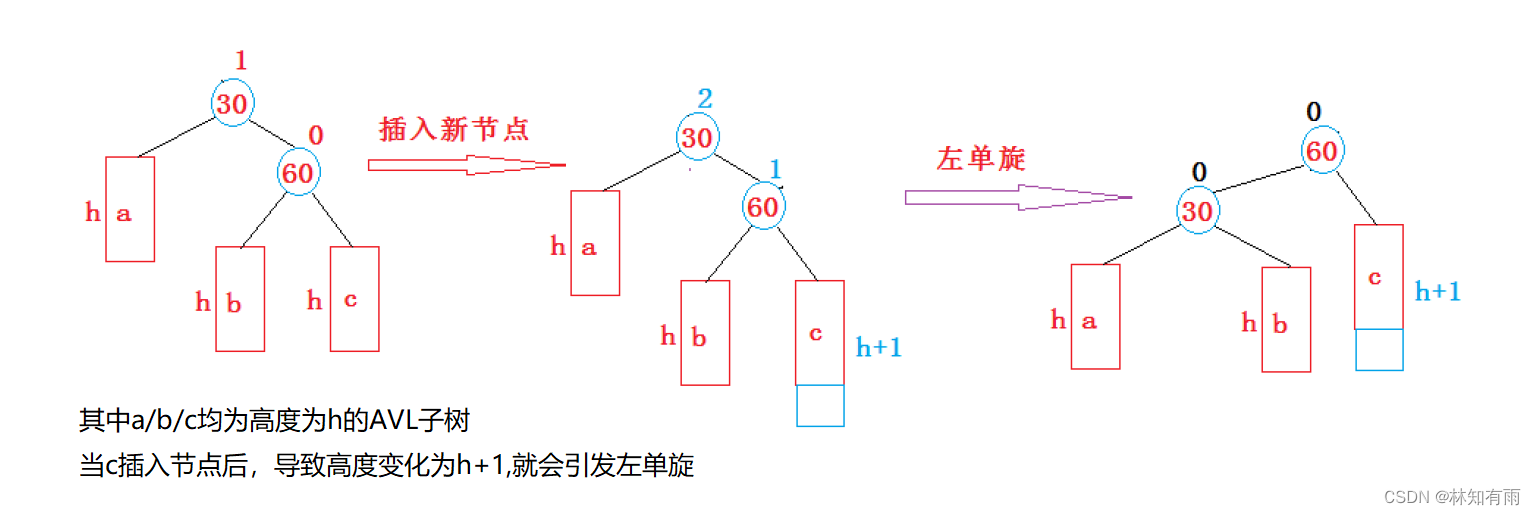
步骤：1、将值为60的节点的左子树移到值为30的节点的右指针下

2、再将以值为30的节点的树移到值为60的节点的左指针下 

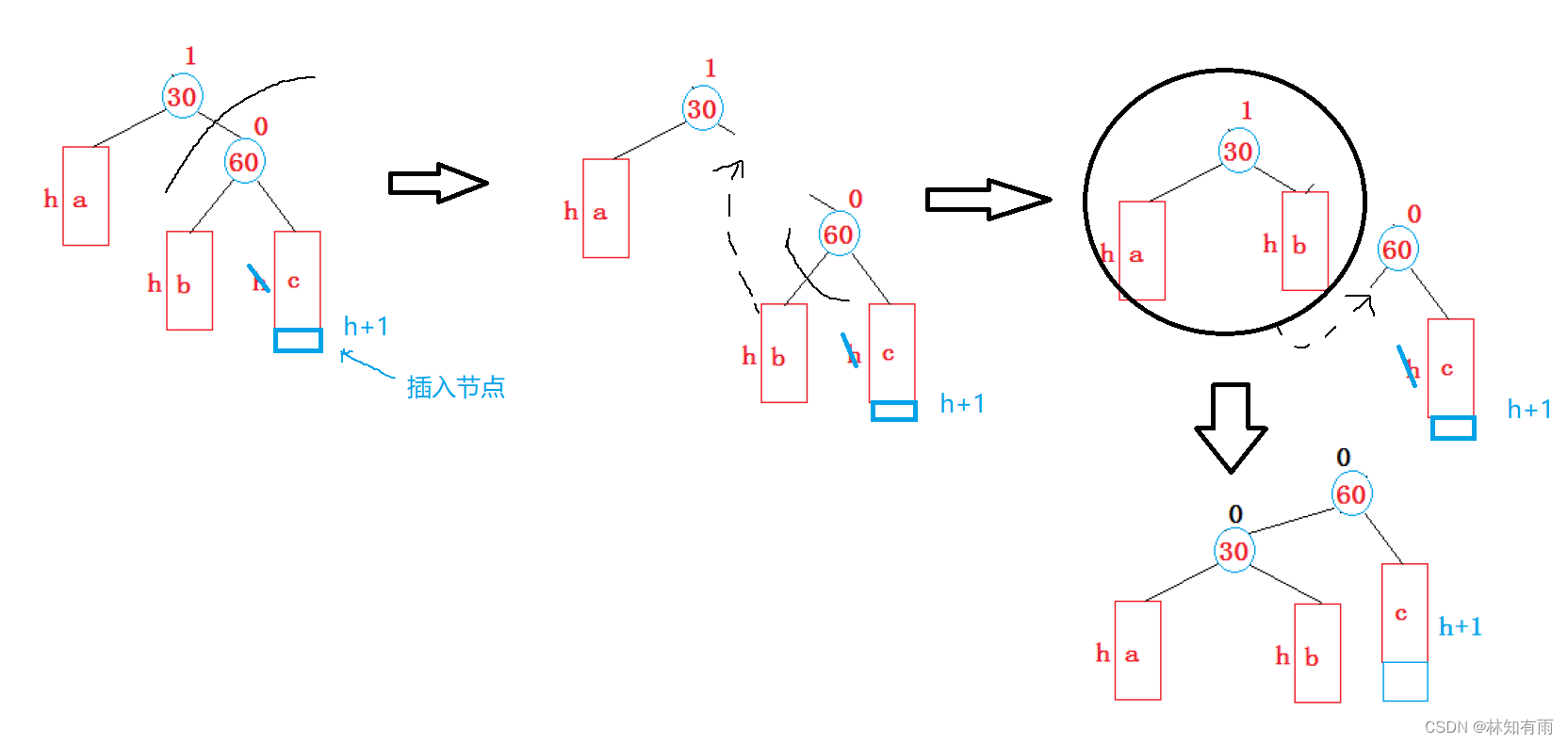
void RotateL(Node* parent){Node* sub = parent->_right;Node* subL = sub->_left;if (subL)subL->_parent = parent;Node* ppnode = parent->_parent;parent->_right = subL;sub->_left = parent;parent->_parent = sub;if (ppnode == nullptr){_root = sub;_root->_parent = nullptr;}else{if (ppnode->_right == parent)ppnode->_right = sub;else if (ppnode->_left == parent)ppnode->_left = sub;sub->_parent = ppnode;}//重新更新平衡因子sub->_bf = 0;parent->_bf = 0;}

情况2：新节点插入较深左子树的左侧---左左：右单旋 

步骤：1、将值为30的节点的右子树移到值为60的节点的左指针下

2、再将以值为60的节点的树移到值为30的节点的右指针下 

代码与左单旋类似

void RotateR(Node* parent){Node* sub = parent->_left;Node* subR = sub->_right;if (subR)subR->_parent = parent;Node* ppnode = parent->_parent;parent->_left = subR;sub->_right = parent;parent->_parent = sub;if (ppnode == nullptr){_root = sub;_root->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = sub;else if (ppnode->_right == parent)ppnode->_right = sub;sub->_parent = ppnode;}sub->_bf = 0;parent->_bf = 0;}

情况3：新节点插入较高左子树的右侧---左右：先左单旋再右单旋  -- 左右双旋

步骤：先以30为轴进行左单旋，再以60为轴进行右单旋

 

 

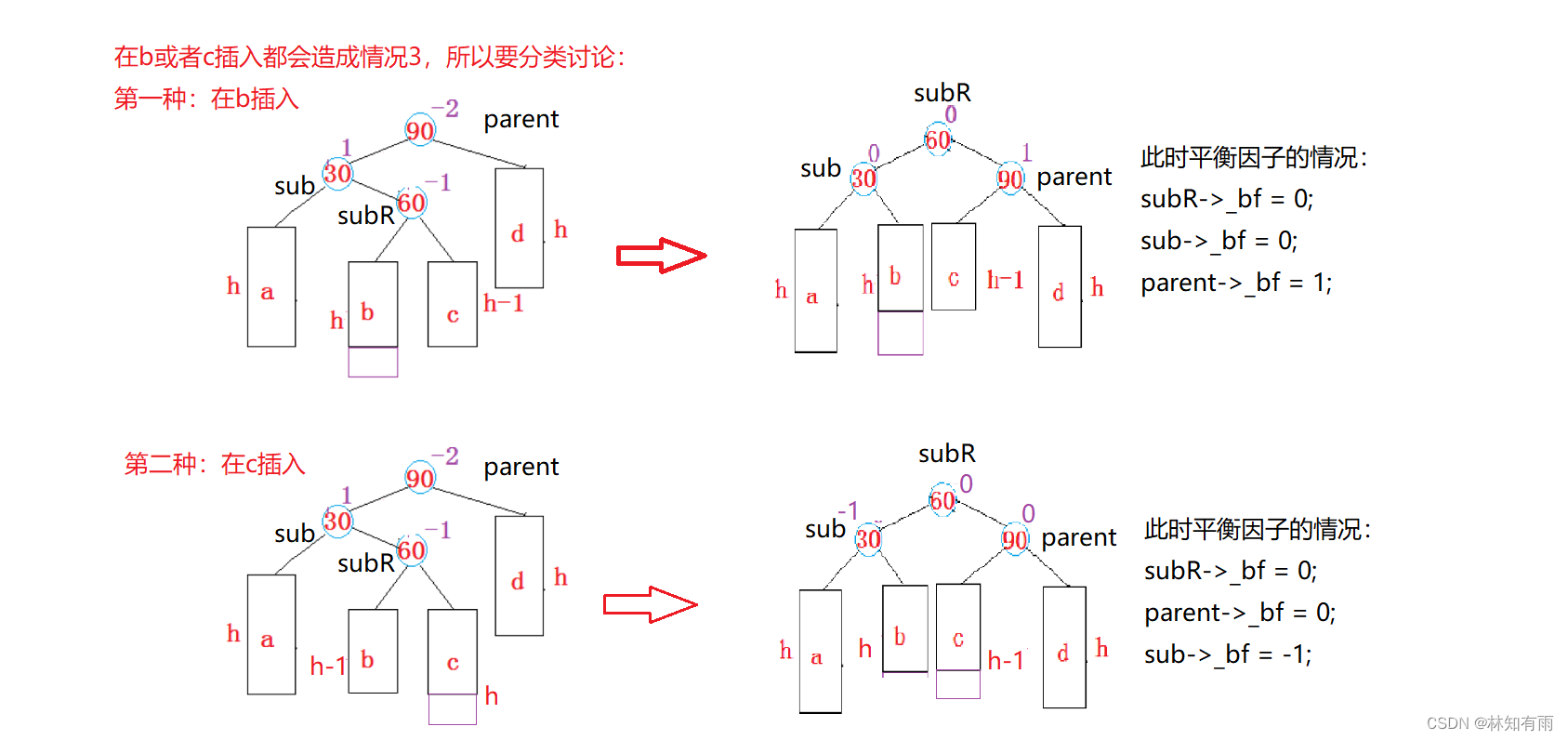
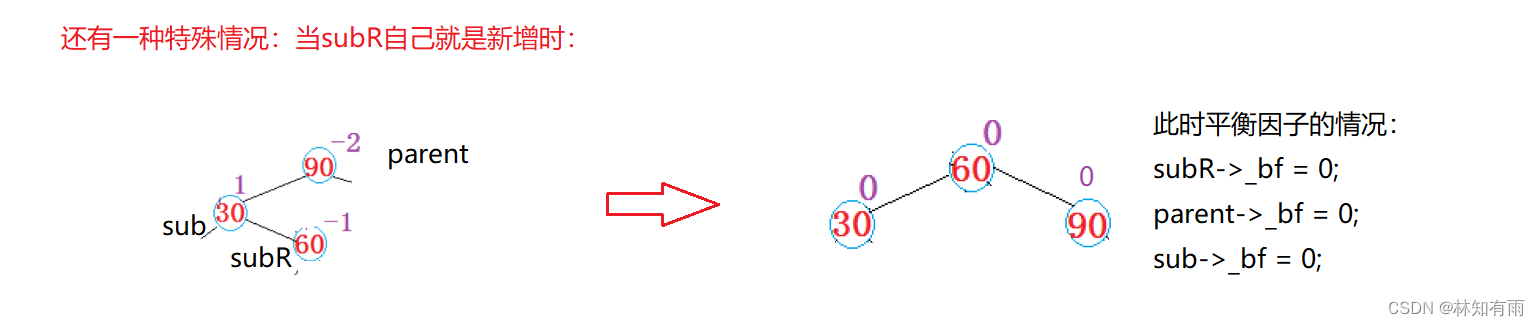
void RotateLR(Node* parent){Node* sub = parent->_left;Node* subR = sub->_right;int bf = subR->_bf; //记录subR的_bf来判断是左插入还是右插入...RotateL(parent->_left);RotateR(parent);if (bf == -1) //subR左子树新增{sub->_bf = 0;parent->_bf = 1;subR->_bf = 0;}else if (bf == 1) //subR右子树新增{parent->_bf = 0;sub->_bf = -1;subR->_bf = 0;}else if (bf == 0) //subR自己就是新增{parent->_bf = 0;sub->_bf = 0;subR->_bf = 0;}elseassert(false);}

 

情况4：新节点插入较高右子树的左侧---右左：先右单旋再左单旋  -- 右左双旋

 

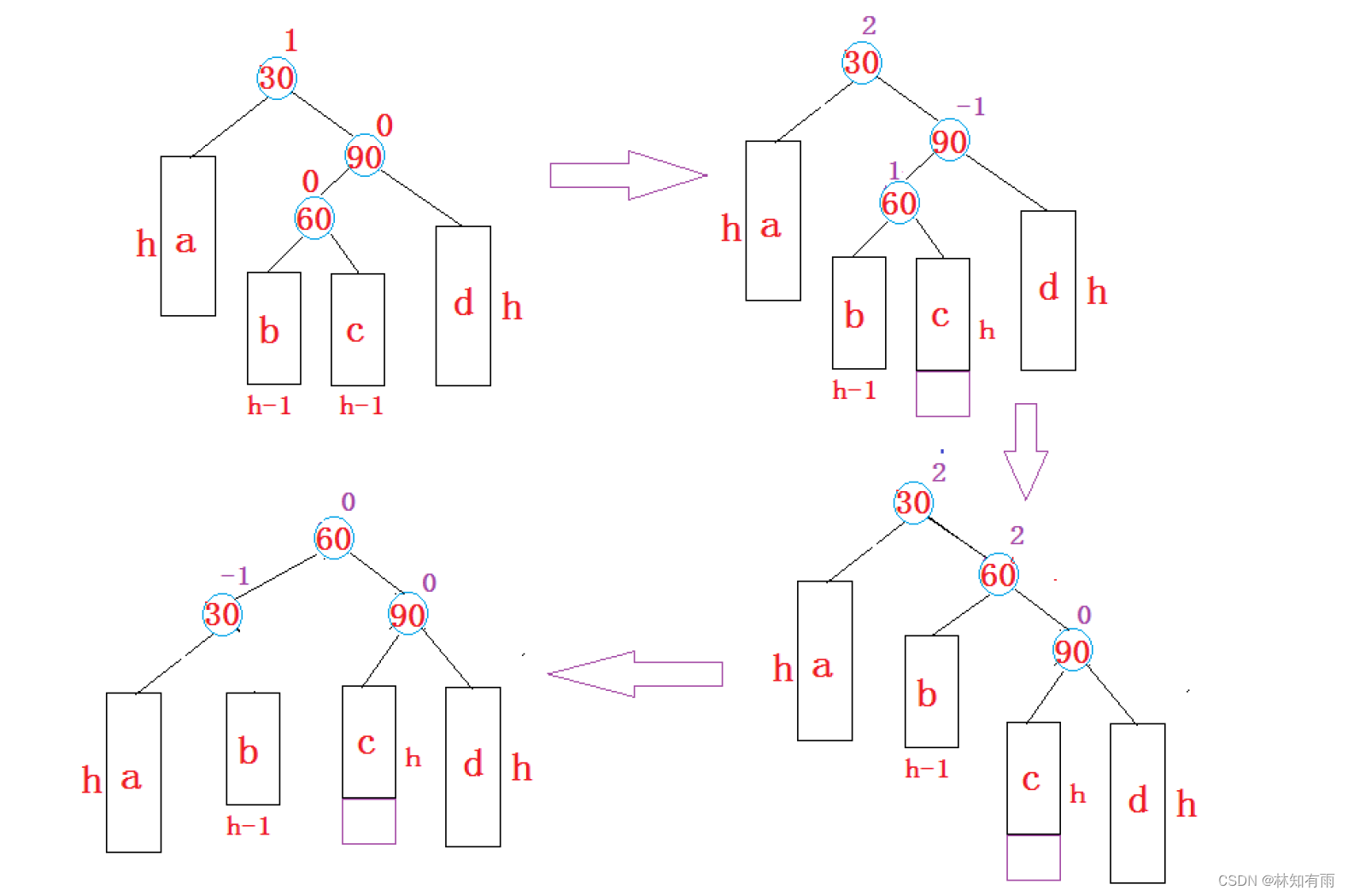
代码与左右双旋类似

void RotateRL(Node* parent){Node* sub = parent->_right;Node* subL = sub->_left;int bf = subL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1){parent->_bf = -1;sub->_bf = 0;subL->_bf = 0;}else if (bf == 0){parent->_bf = 0;sub->_bf = 0;subL->_bf = 0;}else if (bf == -1){parent->_bf = 0;sub->_bf = 1;subL->_bf = 0;}elseassert(false);}

综上可得到AVL数插入节点的整体过程：

bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}elsereturn false;}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//更新平衡因子while (parent){if (cur == parent->_left)--parent->_bf;else++parent->_bf;if (parent->_bf == 0)break;else if (parent->_bf == -1 || parent->_bf == 1){cur = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){if (parent->_bf == 2 && cur->_bf == 1)RotateL(parent);else if (parent->_bf == -2 && cur->_bf == -1)RotateR(parent);else if (parent->_bf == -2 && cur->_bf == 1)RotateLR(parent);else if (parent->_bf == 2 && cur->_bf == -1)RotateRL(parent);break;}}return true;}

3 检验 

要检验一棵树是否为AVL树，可以先检验是否为二叉搜索树，再检验是否平衡树

如下附上代码：

//按照中序遍历打印，若为有序则是二叉搜索树
void _inorder(Node* root) {if (root == nullptr)return;_inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_inorder(root->_right);}

//检验是否为平衡二叉树
int getHeight(Node* root){if (root == nullptr)return 0;int lh = getHeight(root->_left);int rh = getHeight(root->_right);return lh > rh ? lh + 1 : rh + 1;}bool _isBalanced(Node* root){if (root == nullptr)return true;int lh = getHeight(root->_left);int rh = getHeight(root->_right);if (rh - lh != root->_bf)cout << "平衡因子异常" << endl;if (abs(lh - rh) > 2)return false;return _isBalanced(root->_left)&& _isBalanced(root->_right);}

本文着重讲解AVL数的整体构建过程，并未涉及到迭代器和其他等接口的设计，这些内容会在之后讲解红黑树一起加入。

感谢阅读