汉诺塔递归算法精讲
文章目录
- 前言
- 一、汉诺塔是个啥?
- 二、手动解法
- 三、解法抽象
- 四、递归解法
- 五、总结
前言
递归算法是计算机算法中的基础算法,也是非常重要的算法,从某种程度上讲,它有一点儿AI的影子。人脑是可以完成递归思路的,但是对不起,残酷的现实是,一般人脑在精力集中的情况下,能递归个三五层就就基本晕菜了。反正我是这样,你或者您可能深度多一些。当然个别领域,例如棋手,可能深度多达10层或者20层,这是凤毛麟角了。
废话少说,说说汉诺塔的递归解法思路,并给出本人朴素的解释,力图使一看就晕的小伙伴们,能看清楚。
一、汉诺塔是个啥?
尽管您或许知道这个小游戏,但是为了将问题说清楚,还是要简单介绍一下。以下内容来自 《百度百科》
汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
二、手动解法
下面尝试用静态图来分析和描述一下手动解法,大家也可以参考下列链接,以期获得感性认识。
汉诺塔在线游戏
为了简便起见,我们从三个开始尝试。
如图:
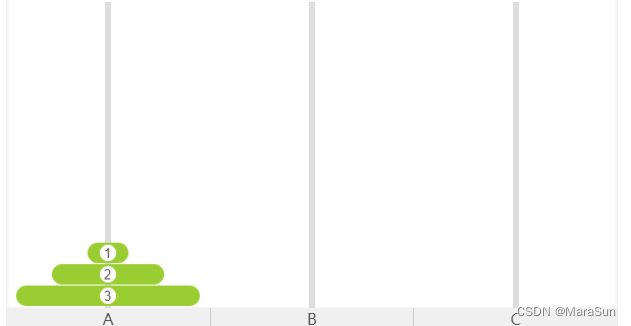
根据题目要求,每次移动一个,而且必须是小的在上面。如果胡乱尝试,您可能好会成功,但是可能会不得要领,因此先分析,才能厘清思路。
分析:我们考虑最后一步,必然是将 1 从什么地方 移到 C 上,倒数第二步,必然是将2 从什么地方移到C上,倒数第三步必然是将3 从什么地方移到C上。因为3 最大,因此,倒数第三步时,必然是3的上面没有盘子,C的上面没有盘子。否则就违背了原则,因此,如果想办法通过什么方法变成下面的情况,倒数第三步就实现了。
如图:
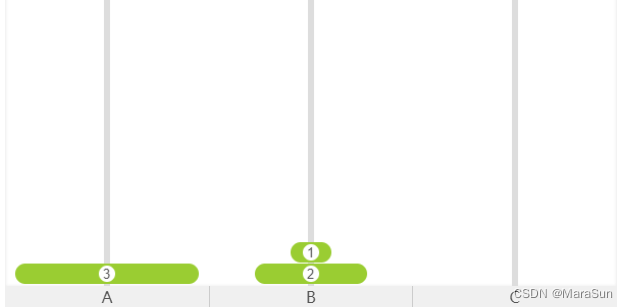
此时就可以把 3 移到 C上,如图
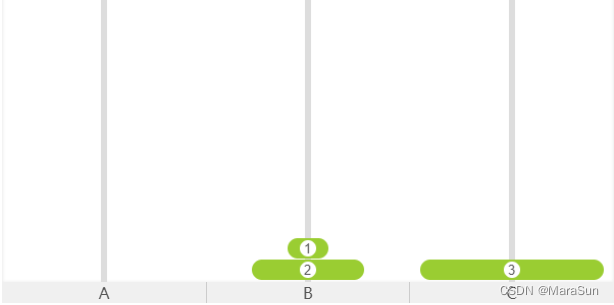
冷静一下,你会发现,此时问题已经降级为,如何将两个盘子移到C上的问题,只是位置从A 变成了B,聪明的你,可以知道这并没有区别。所以现在的问题是 怎么将两个盘子移到到C上。这个问题就非常简单了,1->A, 2->C,1->C。 由于我们遵守小的在上面的原则,就是说每次只能取最上面的 一个 盘子,因此上面的步骤也可以用位置来表示就是
B->A, B->C, A->C, 至于上面的盘子是啥,其本身已经记住了。
OK, 三个已经完成了。
三、解法抽象
现在我们整理一下思路:
要想把3个盘子从A移到C上,必须先把3-1个盘子从A移到B上;套用上面的想法,
做进一步的思考:如果想把3-1个盘子从A移到B上,必需先把 3-1-1个盘子从A移到C上。
仔细看上面的步骤,我们进一步分析其细节,把语言可以精确的描述为:
要想把3(n)个盘子从A 移到C上,必须先把3-1(n-1)个盘子通过C移到B上;
如果想把3-1(n-1)个盘子从A移到B上,比需先把 3-1-1(n-1-1)个盘子通过B移到C上。
可以看出上述的步骤的相似性,就是有三个抽象点,第一:起点, 第二 终点, 第三是:过度点。
仿照上面的思路,我们可以得到 n个盘子的移动方法;
要想把n个盘子移到C上,必须先把n-1个盘子通过C移到B上;
采用更抽象的描述就是:
要想把n个盘子从 起点 移到 终点上,必须先把n-1个盘子通过 终点 移到 过渡点上;
我们用 From 表示起点,To 表示终点 , By 表示过渡点,那么上面的描述就是
要想把n个盘子从from 移到 to ,必须先把n-1个盘子通过 to 移到 by 上;
进一步,假设我们完成了一个过程,叫 HanoiMove, 根据上面的分析,它必须包括四个关键属性: 个数n,起点 from,过渡点 by,终点 to,我们不妨记作
HanoiMove(n,from, by, To) ,这个表示 把 n 个盘子从From 经过 by, 移到到 To,聪明的你应该看出来这不就是函数吗?为了更清楚起见,我们采用 相应的位置表示起点,过渡点和终点。
四、递归解法
根据上面的分析,我们只要逐层降级就可以完成任务了,这就用到了递归,为了说清楚,我们慢慢来。
第一步:调用 HanoiMove(n,from, by, To) ,表示将n从 From 经过 by 移到 To 上。
第二步:HanoiMove(n-1,from, by, To ) ,这个表示 将n-1个盘子,从 from 经过to移到 by 上
第三步:此时From 上面只有一个 最大号的 盘子了 ,编号n,只需 将 编号n的盘子从 From 移动到 to上就可以了。注意此时是移动一个盘子,没有递归的问题。
第四步:这个时候, n-1个盘子 在 by 上面(by成为起点了,from 是过渡点, to仍然是终点), 调用前面的过程 HanoiMove(n-1,by, from, to ) 这个表示 将n-1个盘子,从 by 经过From移到 to上
到这一步就完成了所有的盘子的搬运。
写成伪代码的函数就是:
HanoiMove(n,from, by, To){HanoiMove(n-1,from, by, To ) 输出:From->toHanoiMove(n-1,by, from, to )
}
但是这样就行了吗?
递归调用的一个关键就是结束条件,如果没有,就会一直递归下去,直到溢出错误出现。上面的伪代码中,没有结束条件,那么结束条件是什么呢?显然是n=1 的时候,就结束了。因此,加上结束条件之后的代码为:
HanoiMove(n,from, by, To){if(n==1) {输出:From->toreturn }HanoiMove(n-1,from, by, To ) 输出:From->toHanoiMove(n-1,by, from, to )
}
可以将上述伪代码,改编成某种语言运行
其C#代码如下:
public void HanoiMove(int n, string from, string by, string to){if (n > 1){HanoiMove(n - 1, from , to, by);Console.WriteLine( String.Format("\r\n{0} {1}->{2}", n, from, to));//是盘子编号,可以不用。HanoiMove(n - 1, by, from, to);}else{Console.WriteLine( String.Format("\r\n{0} {1}->{2}", n, from, to));}}
注意:上面的输出的n 可以不用。
五、总结
对于递归调用的代码实现,一定要将过程抽象出来,反复的在头脑中进行这一过程的拟合,将具体步骤进行高度的抽象,具化成参数和表达式(输出),并设置结束条件(递归出口)。
MaraSunDB BJFWDQ 2023-02-15
`
相关文章:

汉诺塔递归算法精讲
文章目录前言一、汉诺塔是个啥?二、手动解法三、解法抽象四、递归解法五、总结前言 递归算法是计算机算法中的基础算法,也是非常重要的算法,从某种程度上讲,它有一点儿AI的影子。人脑是可以完成递归思路的,但是对不起…...

vue的$nextTick的原理
参考:https://cloud.tencent.com/developer/article/1633546 总结一下:就是$nextTick将回调函数放到微任务或者宏任务当中以延迟它地执行顺序;(总结的也比较懒👶) 重要的是理解源码中它的三个参数的意思&a…...

前端学习第一阶段——第五章CSS(下)
5-9 浮动 08-浮动导读 09-传统网页布局三种方式 10-为什么需要浮动 11-什么是浮动 12-浮动特性-脱标 13-浮动特性-浮动元素一行显示 14-浮动特性-浮动元素具有行内块特性 15-浮动元素经常搭配标准流的父元素 16-浮动布局练习1 <!DOCTYPE html> <html lang"en&quo…...
基于django搭建简单的个人博客
文章目录第一步、在Ubuntu中安装虚拟环境并进入第二步、安装blog所需要的包,在requirements.txt中安装mysqlclient可能会报错,输入下列命令后在安装即可成功第三步、创建好数据库,把测试数据导入第四步、修改DjangoBlog包中 settings中数据库…...

JVM解释器与JIT编译器如何并存?
[1] JVM解释器 JVM设计的初衷仅仅只是为了满足Java程序实现跨平台特性,因此避免采用静态编译的方式直接生成本地机器指令,从而诞生了实现解释器在运行时采用逐行解释字节码的执行程序。 解释器真正意义上所承担的角色就是一个运行时“翻译者”࿰…...
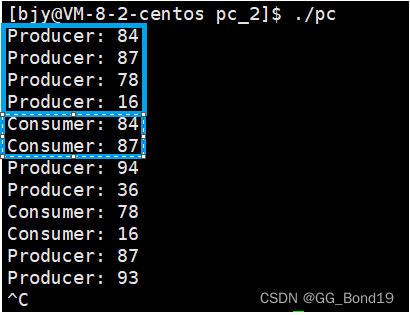
生产者消费者模型
目录 一、生产者消费者模型的概念 二、生产者消费者模型的特点 三、生产者消费者模型优点 四、基于BlockingQueue的生产者消费者模型 4.1 基本认识 4.2 模拟实现 一、生产者消费者模型的概念 生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题 生产者和…...

mysql索引--实例
学生表:Student (Sno, Sname, Ssex , Sage, Sdept) 学号,姓名,性别,年龄,所在系 Sno为主键 课程表:Course (Cno, Cname,) 课程号,课程名 Cno为主键 学生选课表:SC (Sno, Cno, Score)…...

浅聊一下,可中断锁(ReentrantLock)
前言 今天早上上厕所,上的我痔疮犯了,屁股一坐下去就感觉一根针在刺我,得的是外痔,之前还坚持用痔疮膏来着,但是感觉涂药的那个姿势以及位置我实在无法忍受,就把它给断了,到头来还是屁股糟了罪&…...

关于Arcgis林业数据处理的62个常用技巧
一、计算面积 ( 可以帮我们计算小班面积 ) 添加 AREA 字段,然后右键点击字段列,然后点击 CALCULATE VALUES; ---> 选择 ADVANCED --》把下面的代码输入,然后在最下面 处写 OUTPUT 点击 OK 就 OK 了。 Dim Outp…...
一些NLP术语
一些NLP术语pre-training(预训练)fine-tuning(微调)下游任务Few-shot Learning(少样本学习)Prompt?(自然语言提示信息)二级标题三级标题pre-training(预训练&…...

Session详解,学习 Session对象一篇文章就够了
目录 1 Session概述 2 Session原理 3 Session使用 3.1 获取Session 3.2 Session保存数据 3.3 Session获取数据 3.4 Session移除数据 4 Session与Request应用区别 4.1 Session和request存储数据 4.2 获取session和request中的值 4.3 session和request区别效果 5 Sess…...
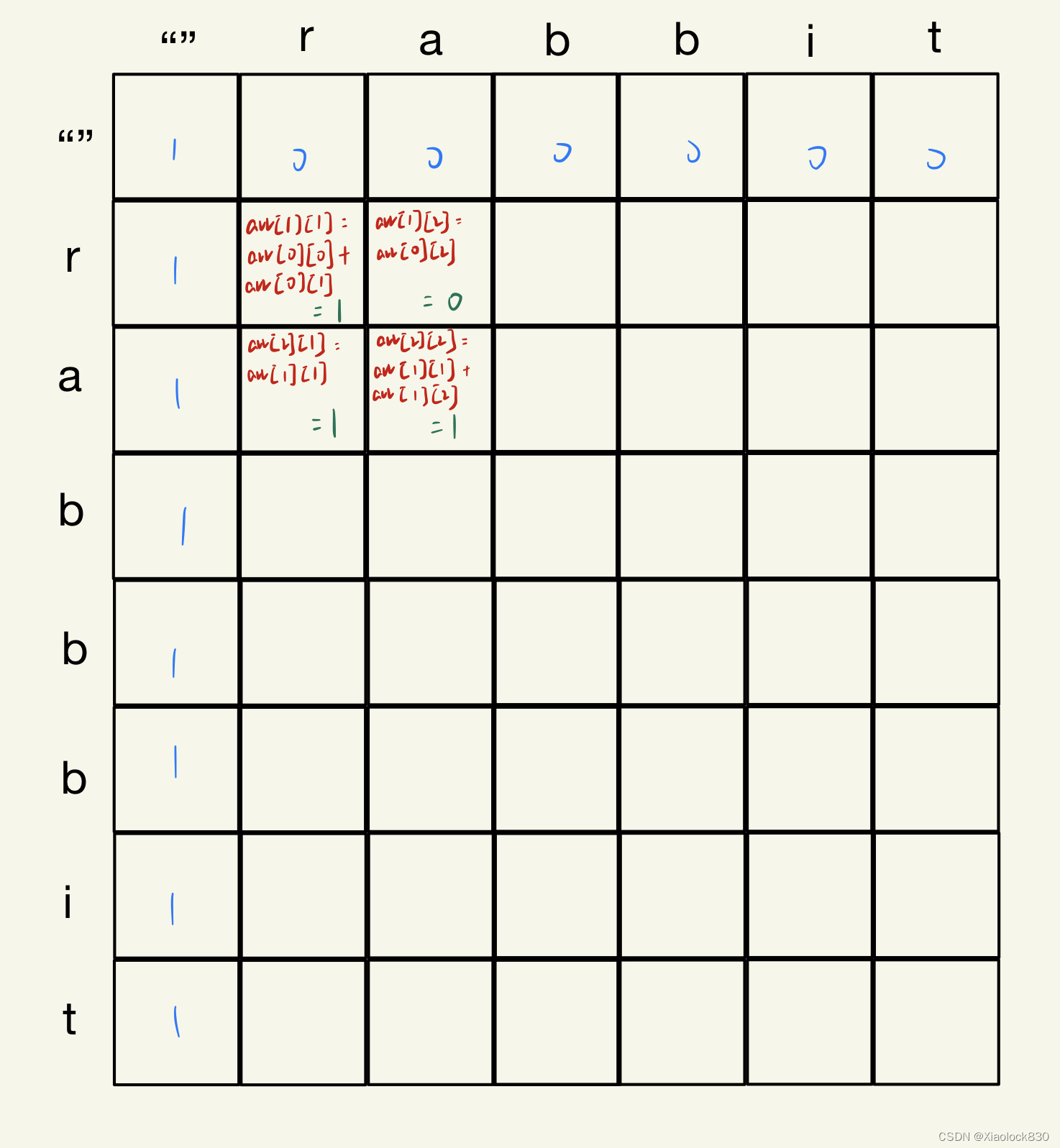
Java——不同的子序列
题目链接 leetcode在线oj题——不同的子序列 题目描述 给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。 字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新…...

Git 基本操作之Git GUI界面和git命令行如何选择
1. 为啥推荐使用git命令行 我发现公司有很多的同事都喜欢使用git的GUI界面工具,喜欢鼠标点点点就完成了代码的提交,这种方式的确是比较简单便捷,但是却存在风险。先上一个事故给大家醒醒脑。 VScode Git 界面操作引发的惨案 上面的惨案是VS…...

Python编程 动态爱心
作者简介:一名在校计算机学生、每天分享Python的学习经验、和学习笔记。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.所用库 1.random简介 2.math 简介 3.tkinter库的简介 二.实际图 三.…...

JavaScript :基础语法
位置: HTML 中的 Javascript 脚本代码必须位于 <script> 与 </script> 标签之间。 JavaScript 输出方式 window.alert() 弹出警告框。document.write() 将内容写到 HTML 文档中。innerHTML 写入到 HTML 元素。console.log() 写入到浏览器的控制台。 …...

buu [AFCTF2018]Single 1
题目描述: Jmqrida rva Lfmz (JRL) eu m uqajemf seny xl enlxdomrexn uajiderc jxoqarerexnu. Rvada mda rvdaa jxooxn rcqau xl JRLu: Paxqmdyc, Mrrmjs-Yalanja mny oekay. Paxqmdyc-urcfa JRLu vmu m jxiqfa xl giaurexnu (rmusu) en dmnza xl jmrazxdeau. Lxd …...

Linux C++ 200行完成线程池类
文章目录1、atomic使用2、volatile关键字3、条件变量4、成员函数指针使用5、线程池6、主线程先退出对子线程影响7、return、exit、pthread_exit区别8、进程和线程的区别1、atomic使用 原子操作,不可分割的操作,要么完整,要么不完整。 #includ…...

C语言指针剖析(初阶) 最详细!
什么是指针?指针和指针类型野指针指针运算指针和数组二级指针指针数组什么是指针?指针是内存中一个最小单元的编号,也就是地址。1.把内存划分为一个个的内存单元,一个内存单元的大小是一个字节。2.每个字节都给定唯一的编号&#…...

AcWing语法基础课笔记 第三章 C++中的循环结构
第三章 C中的循环结构 学习编程语言语法是次要的,思维是主要的。如何把头脑中的想法变成简洁的代码,至关重要。 ——闫学灿 学习循环语句只需要抓住一点——代码执行顺序! while循环 可以简单理解为循环版的if语句。If语句是判断一次…...
A simple freeD tracking protocol implementation written in golang
可以使用的go版本freed调试代码 可以通过udp发送和接收数据 What is freeD? freeD is a very simple protocol used to exchange camera tracking data. It was originally developed by Vinten and is now supported by a wide range of hard- and software including Unreal…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
