统计学期末复习整理
统计学:描述统计学和推断统计学。计量尺度:定类尺度、定序尺度、定距尺度、定比尺度。
描述统计中的测度: 1.数据分布的集中趋势 2.数据分布的离散程度 3.数据分布的形状。
离散系数 也称为标准差系数,通常是用一组数据的标准差与其平均数之比计算 C . V . = s x ‾ C.V.=\frac{s}{\overline{x}} C.V.=xs
离散系数的作用主要用于比较不同总体或样本数据的离散程度,越小说明数据离散程度小。
四种概率抽样方法
1.简单随机抽样 :从含有 N N N个元素的总体中,抽取 n n n个元素作为样本,使得每一个容量为 n n n的样本都拥有相同的概率被抽中。分为重复抽样和不重复抽样两种方法。2.分层抽样 :在抽样之前先将总体的元素划分为若干层,然后从各个层中抽取一定数量的元素组成一个样本。在分层时,应使层内各元素差异尽量小,层与层之间差异尽可能大。采取分层抽样时,为了保持样本结构与总体结构相同,通常采用按比例抽样,按各层元素数占总体元素数的比例从中抽取样本。3.系统抽样:先将总体中元素按某种顺序排列,并按某种规则确定一个随机起点,然后每隔一定的间隔抽取一个元素,直至抽取 n n n个元素形成一个样本,又称等距抽样或机械抽样。4.整群抽样:在抽样之前先将总体的元素划分为若干群,然后以群作为抽样单位从中抽取部分群,再对抽中的各个群所包含的元素进行观察。
中心极限定理设从均值为 μ \mu μ,方差为 σ 2 \sigma^2 σ2的任意一个总体中抽取容量为 n n n的随机样本,则当 n n n充分大时,样本均值 x ‾ \overline{x} x的抽样分布近似服从均值为 μ \mu μ,方差为 σ 2 / n \sigma^2/n σ2/n的正态分布。
点估计的评价准则
无偏性:样本估计量的数学期望应等于被估计总体参数的真值。对于总体的一个未知参数可以有不同的无偏估计量。有效性:令 θ 1 ^ 和 θ 2 ^ \hat{\theta_1}和\hat{\theta_2} θ1^和θ2^是总体未知参数 θ \theta θ的两个无偏估计量,所谓有效性是指样本容量 n n n相同的情况下 θ 1 ^ \hat{\theta_1} θ1^对应的观测值较 θ 2 ^ \hat{\theta_2} θ2^对应的观测值更为集中于 θ \theta θ的真值附近,即 D ( θ 1 ^ ) < D ( θ 2 ^ ) D(\hat{\theta_1})<D(\hat{\theta_2}) D(θ1^)<D(θ2^),则称 θ 1 ^ \hat{\theta_1} θ1^是较 θ 2 ^ \hat{\theta_2} θ2^有效的估计量。一致性:当样本容量增大,即当 n n n趋近于无穷大的时候,要求 θ ^ \hat{\theta} θ^依概率收敛于 θ ^ \hat{\theta} θ^,即 lim n → + ∞ P ( ∣ θ ^ − θ ∣ < ξ ) = 1 ( ξ 为任意小的正数 ) \lim_{n \to +\infty}P(|\hat{\theta}-\theta|<\xi)=1(\xi为任意小的正数) limn→+∞P(∣θ^−θ∣<ξ)=1(ξ为任意小的正数)
区间估计 :区间估计是在点估计的基础上,根据给定的置信度估计总体参数取值范围的方法。影响因素有数据离散度、样本容量、置信水平。
在区间估计中,由样本统计量所构成的总体参数的估计区间称为置信区间,区间最小值称为置信下界,区间最大值称为置信上界。一般的将构造置信区间的步骤重复很多次,置信区间包含总体参数真值的次数所占的比例称为置信水平。
区间估计的步骤
(1)确定置信水平 ( 1 − α ) (1-\alpha) (1−α),然后查表确定其 z α / 2 z_{\alpha/2} zα/2值。(2)计算样本的均值 x ‾ \overline{x} x和标准差 σ x ‾ \sigma_{\overline{x}} σx。(3)确定置信区间: x ‾ ± z α / 2 ∗ σ x ‾ \overline{x}\pm z_{\alpha/2}*\sigma_{\overline{x}} x±zα/2∗σx。在相同置信水平下, n n n较大时,置信区间较短,区间估计精度较高。
(1)总体服从正态分布且总体方差 σ 2 \sigma ^2 σ2已知时,样本均值 x ‾ \overline{x} x的抽样分布均为正态分布,数学期望为总体均值 μ \mu μ,方差为 σ 2 n \frac{\sigma ^2}{n} nσ2,总体均值 μ \mu μ的置信区间: x ‾ ± z α / 2 ∗ σ n \overline{x} \pm z_{\alpha/2}*\frac{\sigma}{\sqrt{n}} x±zα/2∗nσ。
总体比例的区间估计
在大样本情况下,用样本比例 p p p来代替 π \pi π,这时总体比例 π \pi π的置信区间为 p ± z α / 2 p ( 1 − p ) / n p\pm z_{\alpha /2}\sqrt{p(1-p)/n} p±zα/2p(1−p)/n
假设检验的原理:假设检验也成为显著性检验,是事先作出一个关于总体参数的假设,然后利用样本信息来判断原假设是否合理,即判断样本信息与原假设是否有显著差异,从而决定应接受或否定原假设的统计推断方法。
对总体作出的统计假设进行检验的方法依据是概率论中的"在一次试验中小概率事件几乎不发生"原理。
假设检验的步骤:
(1)根据问题要求提出原假设 H 0 H_0 H0和备择假设 H 1 H_1 H1。(2)确定适当的检验统计量(根据中心极限定理)及相应的抽样分布。(3)选取显著性水平 α \alpha α,确定原假设 H 0 H_0 H0的接受域和拒绝域。
显著性水平表示原假设 H 0 H_0 H0为真时拒绝 H 0 H_0 H0的概率,即拒绝原假设所冒的风险。(4)计算检验统计量的值。(5)作出统计决策。
假设检验中的两类错误
第一类错误:原假设 H 0 H_0 H0为真,但作出拒绝原假设的判断,也称弃真错误。
犯此类错误的概率用 α \alpha α表示,所以也称 α \alpha α错误, P ( 拒绝 H 0 ∣ H 0 为真 ) = α P(拒绝H_0|H_0为真)=\alpha P(拒绝H0∣H0为真)=α。
第二类错误:原假设 H 0 H_0 H0为假,但作出接受原假设的判断。
犯此类错误的概率用 β \beta β表示,所以也称 β \beta β错误, P ( 接受 H 0 ∣ H 0 为假 ) = β P(接受H_0|H_0为假)=\beta P(接受H0∣H0为假)=β。
假设检验中的P值
P值的含义: P值是指在原假设 H 0 H_0 H0为真时,样本统计量落在其观测值以外的概率,即表示在实际原假设为真的情况下,拒绝 H 0 H_0 H0犯错误的概率,也成为观测到的显著性水平或相关概率值。
P值和假设检验中的显著性水平的区别: P值有效的补充了 α \alpha α提供的关于检验结果可靠性的有限信息,利用统计量根据显著性水平 α \alpha α作出决策,如果拒绝原假设,也仅仅知道决策犯错误的概率,而P值则是犯错误的实际概率。
第十章 卡方 χ 2 \chi^2 χ2分布与拟合优度检验
1. χ 2 \chi^2 χ2统计量与分布: χ 2 = ∑ ( f 0 − f e ) 2 f e \chi^2=\sum\frac{(f_0-f_e)^2}{f_e} χ2=∑fe(f0−fe)2, f 0 f_0 f0为某一类别的观测值频数, f e f_e fe为某一类别的期望值频数(建立在原假设 H 0 H_0 H0成立的前提下)
2. χ 2 \chi^2 χ2分布特征:② χ 2 \chi^2 χ2分布与自由度有关,自由度越小,越向左边倾斜,随着自由度的增加, χ 2 \chi^2 χ2分布将逐步趋近于对称,即正态分布。(一般认为 n n n>45)③数据呈右偏分布。 χ 2 \chi^2 χ2检验一般是单侧检验,其尾部为拒绝域,由显著性水平 α \alpha α决定。
拟合优度检验
1.概念:用于检验原假设 H 0 H_0 H0是否正确,而该原假设 H 0 H_0 H0通常表述为一个随机变量的总体分布服从一个特定的形式。拟合优度检验是检验随机样本的总体分布与某种特定分布拟合的程度,也就是检验观测值与理论值之间的接近程度(在一定的显著性水平上)。
2.自由度的确定: d f = k − m − 1 df=k-m-1 df=k−m−1, k k k为数据类别的个数, m m m为样本数据中估计的参数个数。
例10.2某公司工资数据如下:工资段 20 − 30 , 30 − 40 , 40 − 50 , 50 − 60 , 60 − 70 , 70 − 80 , 80 − 90 20-30,30-40,40-50,50-60,60-70,70-80,80-90 20−30,30−40,40−50,50−60,60−70,70−80,80−90分别有 5 , 21 , 40 , 45 , 30 , 17 , 7 5,21,40,45,30,17,7 5,21,40,45,30,17,7人。试检验工资的分布是否服从均值为 55.03 55.03 55.03,标准差为 13.56 13.56 13.56的正态分布( α = 0.01 \alpha=0.01 α=0.01).。
第一步,计算期望值频数 f e f_e fe
(1)计算Z值,选择40-50区间为例计算。
Z 1 = X − μ σ = 40 − 55.03 13.56 = − 1.11 , Z 2 = 50 − 55.03 13.56 = − 0.37 Z_1=\frac{X-\mu}{\sigma}=\frac{40-55.03}{13.56}=-1.11,Z_2=\frac{50-55.03}{13.56}=-0.37 Z1=σX−μ=13.5640−55.03=−1.11,Z2=13.5650−55.03=−0.37
由Z值的几何意义,我们知道-1.11,-0.37是数据偏离均值55.03的程度。
(2)求标准正态分布下-1.11~-0.37之间正态分布曲线下的面积,求得为0.2222。
(3)期望值频数 f e f_e fe=165*0.2222=36.663.。
第二步, χ 2 \chi^2 χ2检验
(1) H 0 H_0 H0:总体服从正态分布, H 1 H_1 H1总体不服从正态分布
(2)查表得 χ 2 ( α = 0.01 , d f = 4 ) = 13.277 \chi^2(\alpha=0.01,df=4)=13.277 χ2(α=0.01,df=4)=13.277
(3)计算 χ 2 \chi^2 χ2统计量
(4)因为 χ 2 \chi^2 χ2=3.942102 < < < 13.277,没落在拒绝域内,所以接受原假设,即认为工资数据的分布是服从正态分布的。
相关与回归分析的关系?
答:联系:先进行相关分析再进行回归分析,只有在确定两变量存在着相关分析后,才能分析两变量的回归分析。两变量间的相关程度越大,研究回归才更有意义。通过相关分析,可以大致判断现象与现象之间配合什么数学模型建立回归方程(4分)。
区别:分析的目的不同,相关分析主要分析变量之间有无关系,有多大程度的关系;回归分析用于构建有联系的变量间的回归模型,用于推理变量之间的因果关系。相关分析的两个或两个以上的变量是随机变量。回归分析中的自变量是确定性的变量。(4分)
回归分析:
缺点:样本容量 n n n较小时,仅凭相关系数较大还不足以说明变量有密切关系,当 n n n较大时,相关系数绝对值容易偏小。
回归平方和 S S R = ∑ ( y ^ − y ‾ ) 2 SSR=\sum{(\hat{y}-\overline{y})^2} SSR=∑(y^−y)2,残差平方和 S S E = ∑ ( y i − y ^ ) 2 SSE=\sum{(y_i-\hat{y})^2} SSE=∑(yi−y^)2,总离差平方和 S S T = S S R + S S E SST=SSR+SSE SST=SSR+SSE。
最小二乘法: 原理:使观测值与估计值的离差平方和最小。 y y y的估计值 y ^ = b 0 + b 1 x \hat{y}=b_0+b_1x y^=b0+b1x
b 1 = n ∑ x y − ∑ x ∑ y n ∑ x 2 − ( ∑ x ) 2 , b 0 = y ‾ − b 1 x ‾ b_1=\frac{n\sum{xy-\sum{x}\sum{y}}}{n\sum{x^2}-(\sum{x})^2},b_0=\overline{y}-b_1\overline{x} b1=n∑x2−(∑x)2n∑xy−∑x∑y,b0=y−b1x
多元线性回归的显著性检验
提假设: H 0 : β 1 = β 2 = ⋯ = β m = 0 , H 1 : H_0:\beta_1=\beta_2=\cdots=\beta_m=0,H_1: H0:β1=β2=⋯=βm=0,H1:至少一个回归系数不等于0。
计算统计量 F = S S R / m S S E / n − m − 1 F=\frac{SSR/m}{SSE/n-m-1} F=SSE/n−m−1SSR/m,确定显著性水平和自由度为(m,n-m-1),找临界值 F α F_{\alpha} Fα。若 F > F α F>F_{\alpha} F>Fα,拒绝 H 0 H_0 H0,否则接受并说明所有自变量联合起来对因变量有显著影响。
回归系数的显著性检验
H 0 : β i = 0 H_0:\beta_i=0 H0:βi=0(自变量 x i x_i xi与因变量没有线性关系)
确定 t t t检验的统计量和显著性水平,若 ∣ t ∣ > t α / 2 |t|>t_{\alpha/2} ∣t∣>tα/2,拒绝 H 0 H_0 H0,否则接受。
或者根据给定的P值与方差分析表中的P1值比较,若P1<P则说明该回归系数显著。
方差分析表 : ①m—SSR–SSR/m②n-m-1—SSE—SSE/(n-m-1)
第十二章 时间序列分析
Q:什么是时间序列,有哪些分类? A:时间序列是指一个变量的观测值按照时间顺序排列而成的序列,它反映了现象动态变化的过程和特点,是研究事物发展趋势、规律以及进行预测的依据。分为绝对数、相对数、平均数时间序列。
Q:时间序列的组成因素及其模型? A:组成因素:长期趋势,季节波动,循环波动,不规则波动。
乘法模型是假设时间序列各个构成部分对序列的影响均按照比例变化,加法模型是假设这四种因素对时间序列的影响是可加的。
Q:对时间序列进行平滑以描述其趋势的方法有哪些? A:移动平均法是采用逐项递移的方法分别计算一系列移动的序时平均数,形成一个新的派生序时平均数时间序列。指数平滑法通过对历史时间数列进行逐层平滑计算,从而消除随机因素的影响,识别现象基本变化趋势,并以此来预测未来。
Q:常用时间序列预测方法? 移动平均预测法、指数平滑预测法、线性趋势预测法、自回归预测模型、季节因素分析预测法。
有趋势序列的最小二乘法预测模型:
1.线性趋势模型 Y t ^ = a + b t \hat{Y_t}=a+bt Yt^=a+bt, t t t是时间标号
2.二次曲线趋势模型 Y t ^ = a + b t + c t 2 \hat{Y_t}=a+bt+ct^2 Yt^=a+bt+ct2
有趋势序列的自回归预测模型:
n n n阶自回归模型: Y t ^ = A 0 + A 1 Y t − 1 + A 2 Y t − 2 + ⋯ + A n Y t − n \hat{Y_t}=A_0+A_1Y_{t-1}+A_2Y_{t-2}+\cdots+A_nY_{t-n} Yt^=A0+A1Yt−1+A2Yt−2+⋯+AnYt−n
步骤:①确实最大滞后值 n n n,自由度 t − 2 n − 1 t-2n-1 t−2n−1。②利用表确定自回归方程和临界值③计算检验统计量 t = a n − A n S a n t=\frac{a_n-A_n}{S_{a_n}} t=Sanan−An/如果不拒绝原假设,那么第 n n n个变量被舍弃,重复该步骤。
什么是因子分析 :因子分析是用少量集成后的互不相关的因子变量去解释大量统计变量的一种统计方法,这种方法能以较少的因子变量和最小的信息损失来解释变量之间的结构。
因子分析的步骤 :①根据具体问题,判断待分析的若干原始变量是否适合作因子分析,并采用某些检验方法来判断数据是否符合分析要求②选择提取公因子的方法,并按一定标准确定提取公因子的数目③考察公因子的可解释性,并在必要时进行因子旋转,以寻求最佳的解释方式④计算出因子得分等中间指标,进一步分析使用。
巴特利特球度检验、反映象相关矩阵检验、KMO检验。
什么是方差分析,基本思想和原理: 方差分析就是针对一定因素分析总体的各个因素水平是否有差异。通过对因素水平间方差与因素水平内方差的比较,当这两个方差的比值较小时,方差分析的结果可以认为总体均值相同,否则认为不同。
方差分析中的基本假定 方差分析的前提条件是讨论的总体服从正态分布,其各个总体的方差相等,并且选择的样本是相互独立的。
什么是聚类分析,作用是什么 : 聚类分析主要用于辨别具有相似性的事物,并根据彼此不同的特性加以聚类,使同一类事物具有高度的相似性,不同类事物具有较大的差异性。聚类分析能够从现有的样本数据出发,按照他们的亲疏程度分成若干类,并通过变量与变量的连接状况,揭示在同一类别中不同变量或样本的亲疏程度。
相关文章:

统计学期末复习整理
统计学:描述统计学和推断统计学。计量尺度:定类尺度、定序尺度、定距尺度、定比尺度。 描述统计中的测度: 1.数据分布的集中趋势 2.数据分布的离散程度 3.数据分布的形状。 离散系数 也称为标准差系数,通常是用一组数据的标准差与…...

Sketch在线版免费使用,Windows也能用的Sketch!
Sketch 的最大缺点是它对 Windows/PC 用户不友好。它是一款 Mac 工具,无法在浏览器中运行。此外,使用 Sketch 需要安装其他插件才能获得更多响应式设计工具。然而,现在有了 Sketch 网页版工具即时设计替代即时设计! 即时设计几乎…...

详解uni-app项目运行在安卓真机调试
详解uni-app项目运行在安卓真机调试 uni-app项目运行在安卓真机调试 文章目录 详解uni-app项目运行在安卓真机调试前言为什么要用真机调试?真机调试操作步骤总结 前言 UNI-APP学习系列之详解uni-app项目运行在安卓真机调试 为什么要用真机调试? 因为安…...

体积小、无广告、超实用的5款小工具
大家好,我又来啦,今天给大家带来的5款软件,共同特点都是体积小、无广告、超实用,大家观看完可以自行搜索下载哦。 1.动态桌面——WinDynamicDesktop WinDynamicDesktop是一款用于根据时间和地点自动更换桌面壁纸的工具。它可以让…...

OZON好出单吗?新手如何做?注意事项是什么?
最近OZON的势头确实很猛,东哥后台也收到了很多关于OZON的咨询,很多想尝试跨境电商的新手卖家都对这个平台跃跃欲试,其中问最多的就是,“OZON好出单吗?”“新手做OZON需要注意什么?避开哪些坑?”…...
性能测试需求分析有哪些?怎么做?
目录 性能测试必要性评估 常见性能测试关键评估项如下: 性能测试工具选型 性能测试需求分析 性能测试需求评审 性能测试需求分析与传统的功能测试需求有所不同,功能测试需求分析重点在于从用户层面分析被测对象的功能性、易用性等质量特性ÿ…...

STM32F103RCT6 -- 基于FreeRTOS 的USART1 串口通讯
1. 在STM32F103RCT6 单片机上跑FreeRTOS 实时操作系统,使用串口USART1 通讯,发送 – 接收数据,实现上位机与下位机的通信 使用 FreeRTOS 提供的队列(Queue)机制来实现数据的接收和发送 2. USART1 配置: …...

区间预测 | MATLAB实现基于QRCNN-LSTM-Multihead-Attention多头注意力卷积长短期记忆神经网络多变量时间序列区间预测
区间预测 | MATLAB实现基于QRCNN-LSTM-Multihead-Attention多头注意力卷积长短期记忆神经网络多变量时间序列区间预测 目录 区间预测 | MATLAB实现基于QRCNN-LSTM-Multihead-Attention多头注意力卷积长短期记忆神经网络多变量时间序列区间预测效果一览基本介绍模型描述程序设计…...
)
递归--打印一个字符串的全部排列(java)
打印一个字符串的全部排列 打印一个字符串的全部排列解题思路打印一个字符串的全部排列,要求不要出现重复的排列递归专题 打印一个字符串的全部排列 自负串全排序: 举例: abc 的全排序是: abc acb bac bca cba cab 解题思路 因为每个字符都要选,其实就是选择每个字符…...

【001 设备驱动】主设备号和次设备号的用途
一、请简述主设备号和次设备号的用途 Linux 中每个设备都有一个设备号,设备号由主设备号和次设备号两部分组成,主设备号表示某一个具体的驱动,次设备号表示使用这个驱动的各个设备。 Linux 提供了一个名为 dev_t 的数据类型表示设备号&…...

移动端PDF在线预览
苹果手机可以直接在线预览PDF文件,而安卓手机不行,必须得下载(如图),所以需要解决一下 1.准备所需js文件 (1)js下载地址https://mozilla.github.io/pdf.js/ (2)下载步骤 ①:打开网址后&#x…...

虚拟机两次寻址
一次寻址: 虚拟、逻辑地址:CS(段选择子) eip(段内偏移)> 线性地址 : 32位或64位 通过页表> 物理地址 x86: 页面大小4k pte4个字节 10-10-12 (不管是x86 x86PAE x64下页内偏…...
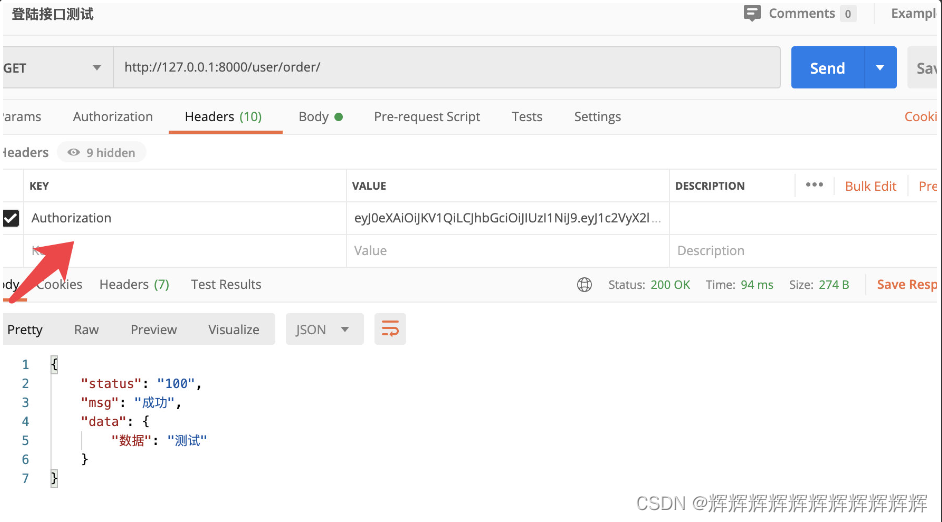
DRF之JWT认证
一、JWT认证 在用户注册或登录后,我们想记录用户的登录状态,或者为用户创建身份认证的凭证。我们不再使用Session认证机制,而使用Json Web Token(本质就是token)认证机制。 Json web token (JWT), 是为了在网络应用环…...

华为OD机试真题 Java 实现【放苹果】【2022Q4 100分】
一、题目描述 把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法? 注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5,1)被视为是同一种分法。 数据范围:0≤m≤10 ,1≤n≤10 。 二、输入描述 输入两个int整数。 三、输出描述 输…...

拼多多继续ALL IN
2023年注定是中国电商不平凡的一年。 随着网购用户数量见顶,经济形势进入新常态,电商平台已经来到了短兵相接的肉搏战阶段。 此刻的618大促,硝烟弥漫,刀光剑影,电商“决战”似乎是迫在眉睫。对各个平台来说,…...

Unity的IPostprocessBuildWithReport:深入解析与实用案例
Unity IPostprocessBuildWithReport Unity IPostprocessBuildWithReport是Unity引擎中的一个非常有用的功能,它可以让开发者在构建项目后自动执行一些操作,并且可以获取构建报告。这个功能可以帮助开发提高工作效率,减少手动操作的时间和错误…...
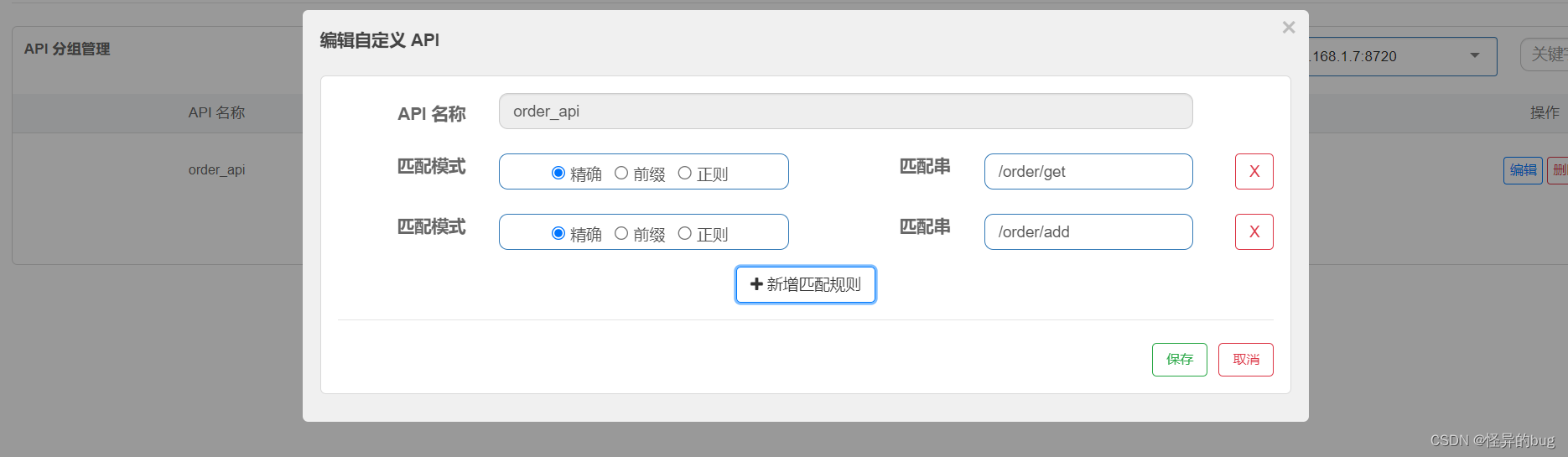
九、Spring Cloud—gateway网关
一、引言 每个微服务都需和前端进行通信,解决每个微服务请求时的鉴权、限流、权限校验、跨域等逻辑,放在一个统一的地方进行使用。 在微服务架构中,网关是一个重要的组件,它作为系统的入口,负责接收所有的客户端请求…...

ARM微架构与程序编写
目录 1.流水线 2.指令流水线 3. 多核处理器编辑 4. 工程搭建 4.1为Keil软件配置编译工具链 5.程序编写 5.1 数据处理指令 5.2 带标志位的加法ADC ADDS 5.3 跳转指令B\BL 5.4 单寄存器内存访问 5.5 批量寄存器内存访问 5.6 栈的应用->叶子函数的调用过程 5.…...
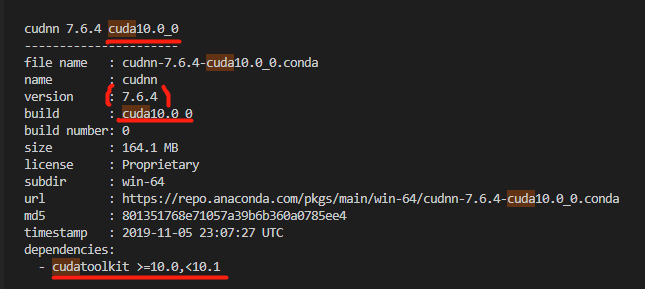
Windows下利用Anaconda创建多个CUDA环境
参考 https://blog.csdn.net/qq_42395917/article/details/126237388 https://blog.csdn.net/qq_42406643/article/details/109545766 (待学习补充) https://blog.csdn.net/qq_43919533/article/details/125694437 (待学习补充) 安装cudatoolkit和cudnn # 前提是我已经安装了…...

C SS复习笔记
1.img标签 img的src属性是图片显示不出来时显示的文字 ing的title属性是光标放到图片上,提示的文字 2.a标签 a标签的target属性表示打开窗口的方式,默认的值是_self表示当前窗口的打开页面,_blank表示新窗口打开页面。 a标签的href链接分…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
