克拉默法则证明(Cramer‘s Rule)
若 n 个方程 n 个未知量构成的非齐次线性方程组:
{ a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 . . . . . . a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n \begin{equation*} \begin{cases} a_{11}x_{1} + a_ {12}x_{2} + ... + a_{1n}x_{n} = b_1 \\ a_{21}x_{1} + a_ {22}x_{2} + ... + a_{2n}x_{n} = b_2 \\ ... ...\\ a_{n1}x_{1} + a_ {n2}x_{2} + ... + a_{nn}x_{n} = b_n \end{cases} \end{equation*} ⎩ ⎨ ⎧a11x1+a12x2+...+a1nxn=b1a21x1+a22x2+...+a2nxn=b2......an1x1+an2x2+...+annxn=bn
的系数行列式 ∣ A ∣ ≠ 0 |A| \neq 0 ∣A∣=0,则方程组有唯一解,且
x i = ∣ A i ∣ ∣ A ∣ , i = 1 , 2 , . . . , n x_i = \frac{|A_i|}{|A|}, i = 1, 2, ..., n xi=∣A∣∣Ai∣,i=1,2,...,n
其中 ∣ A i ∣ |A_i| ∣Ai∣ 是 ∣ A ∣ |A| ∣A∣ 中的 i i i 列元素(即 x i x_i xi 的系数)替换成方程组右端的常数项 b 1 , b 2 , . . . , b n b_1, b2, ..., b_n b1,b2,...,bn 所构成的行列式。
证明:
使用 a 1 , . . . , a n a_1, ..., a_n a1,...,an 表示 A 的列,用 e 1 , . . . , e n e_1, ... , e_n e1,...,en 表示 n × n n\times n n×n的单位阵 I I I的列。由于有 A x = b Ax = b Ax=b,由矩阵乘法:
A ⋅ [ e 1 , . . . , x , . . . , e n ] = [ A e 1 , . . . , A x , . . . , A e n ] = [ a 1 , . . . , b , . . . , a n ] = A i \begin{align*} A\cdot [e_1, ..., x, ..., e_n] &= [Ae_1, ..., Ax, ..., Ae_n] \\ &= [\ \ a_1\ , ...\ , \ b\ \ , ..., a_n] \\ &= A_i \end{align*} A⋅[e1,...,x,...,en]=[Ae1,...,Ax,...,Aen]=[ a1 ,... , b ,...,an]=Ai
记 [ e 1 , . . . , x , . . . , e n ] [e_1, ..., x, ..., e_n] [e1,...,x,...,en] 为 I i ( x ) I_i(x) Ii(x),
两边求行列式:
∣ A ∣ ⋅ ∣ I i ( x ) ∣ = ∣ A i ∣ |A|\cdot|I_i(x)| = |A_i | ∣A∣⋅∣Ii(x)∣=∣Ai∣
其中: ∣ I i ( x ) ∣ = x i |I_i(x)| = x_i ∣Ii(x)∣=xi
所以有: x i = ∣ A i ∣ ∣ A ∣ , ∣ A ∣ ≠ 0 x_i = \frac{|A_i|}{|A|},|A|\neq 0 xi=∣A∣∣Ai∣,∣A∣=0,得证。
相关文章:
)
克拉默法则证明(Cramer‘s Rule)
若 n 个方程 n 个未知量构成的非齐次线性方程组: { a 11 x 1 a 12 x 2 . . . a 1 n x n b 1 a 21 x 1 a 22 x 2 . . . a 2 n x n b 2 . . . . . . a n 1 x 1 a n 2 x 2 . . . a n n x n b n \begin{equation*} \begin{cases} a_{11}x_{1} a_ {12}x_{2}…...

【接口防刷】处理方案
【接口防刷】 欢迎使用【接口防刷】常见的处理方案访问次数和频率限制验证码校验登录校验机制数据交互加密异常监测机制附录 欢迎使用【接口防刷】常见的处理方案 接口防刷处理方案是指为了防止恶意攻击或非法数据采集,采取一系列技术措施来保护接口数据的安全和完…...
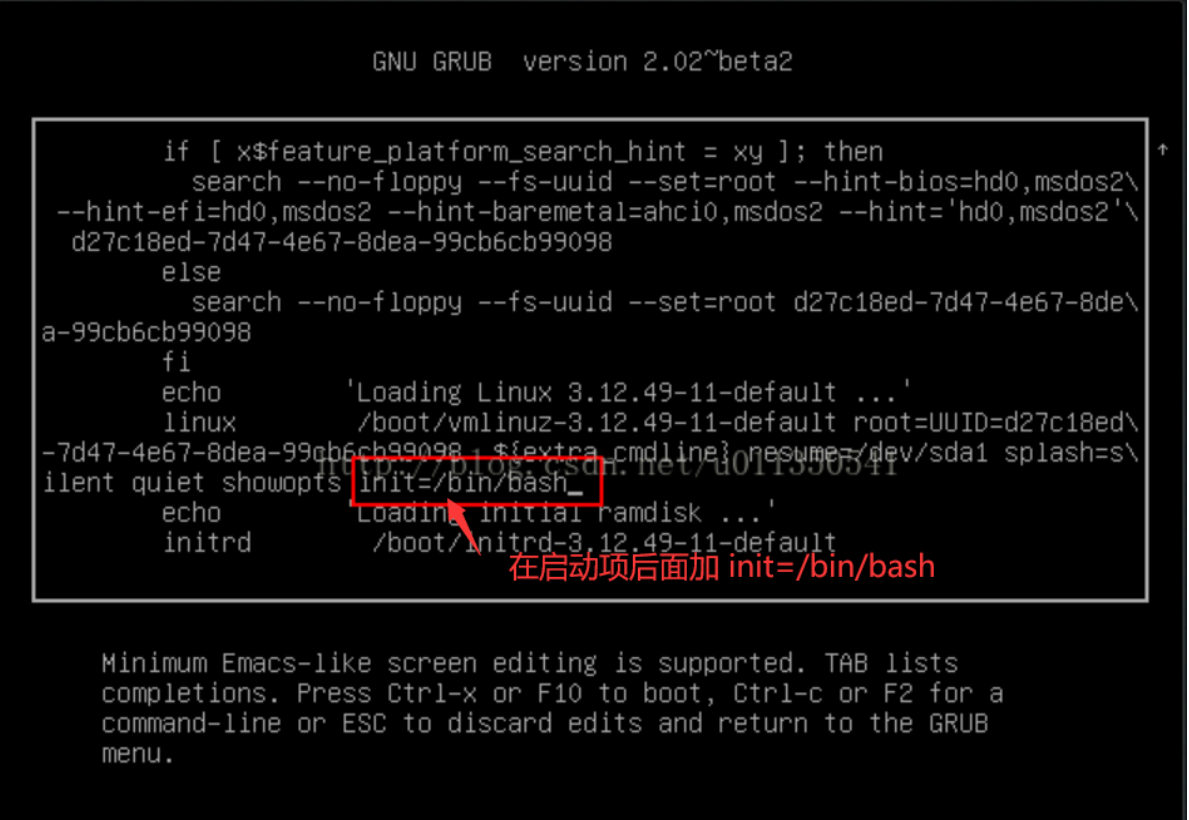
安装Linux-SUSE操作系统
文章目录 一、安装Linux-SUSE系统1、环境准备2、SUSE 镜像的下载2.1、下载企业服务器2.2、ARM和桌面的ISO 3、安装SUSE4、配置本地 yum 源5、SUSE常用安装命令6、在 SUSE系统上安装mysql数据库步骤:7、破解SUSE系统root密码 一、安装Linux-SUSE系统 1、环境准备 操…...

二、机器人的结构设计
1 、螺丝连接的坚固性 坚固性是机器人能顺利完成指定任务的一个重要条件,无论我们程序设计的如何完美, 如果不能保证机器人具有坚固性和稳定性,就无法保证任务的顺利完成,机器人在运行时如 果发生散架和分裂都会影响其功能的实现…...
UITableView学习笔记
看TableView的资料其实已经蛮久了,一直想写点儿东西,却总是因为各种原因拖延,今天晚上有时间静下心来记录一些最近学习的TableView的知识。下面进入正题,UITableView堪称UIKit里面最复杂的一个控件了,使用起来不算难&a…...

Nginx反向代理与负载均衡
简介 Nginx 是一款高性能、轻量级的 Web 服务器软件,常用于反向代理和负载均衡。以下是 Nginx 反向代理和负载均衡的基本原理和实现方式 1、反向代理 当客户端请求访问一个 Web 服务器时,首先会发送请求到 Nginx,然后 Nginx 将请求转…...

Delaunay三角剖分学习笔记
文章目录 Delaunay三角剖分学习笔记1 Voronoi \text{Voronoi} Voronoi图1.1 定义与性质 2 三角剖分2.1 定义与性质2.2 质量(quality)评定标准 3 Delaunay三角剖分3.1 定义3.2 准则与性质 4 Delaunay三角剖分算法4.1 Bowyer-Watson算法4.1.1 算法步骤:4.1.2 算法伪代…...

@Resource和@Autowired的区别
1.相同点 Resource和Autowired这两个注解的作用都是在Spring生态里面去实现Bean的依赖注入 2.不同点 2.1 Autowired 首先,Autowired是Spring里面提供的一个注解,默认是根据类型来实现Bean的依赖注入。 Autowired注解里面有一个required属性默认值是t…...

linux达梦数据库的安装与卸载
一、安装 创建dmdba用户及用户组 创建安装目录: mkdir -p /dm8 创建组 :groupadd dinstall 创建用户 :useradd -g dinstall dmdba 设置密码 :passwd dmdba 创建文件夹:mkdir /dmdata 更改安装目录所有者: c…...
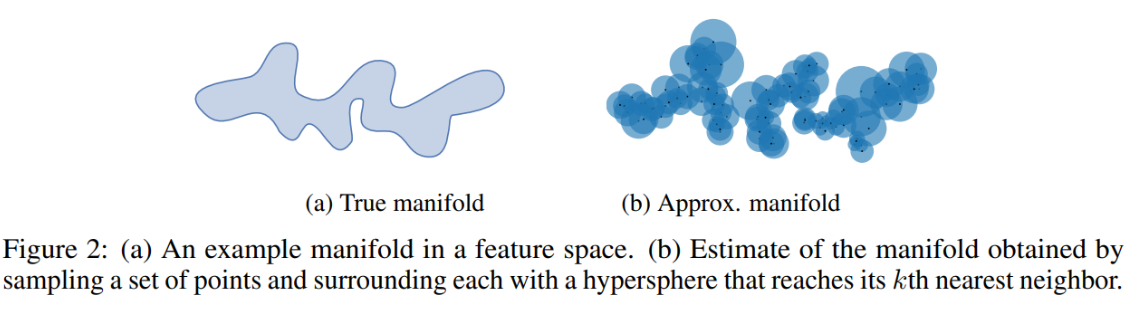
生成式模型的质量评估标准
Sample Quality Matrix 如何评价生成式模型的效果?ISFIDsFIDPrecision & RecallPrecisonRecall计算precision和recall 如何评价生成式模型的效果? Quality: 真实性(逼真,狗咬有四条腿) Diversity: 多样性&#x…...
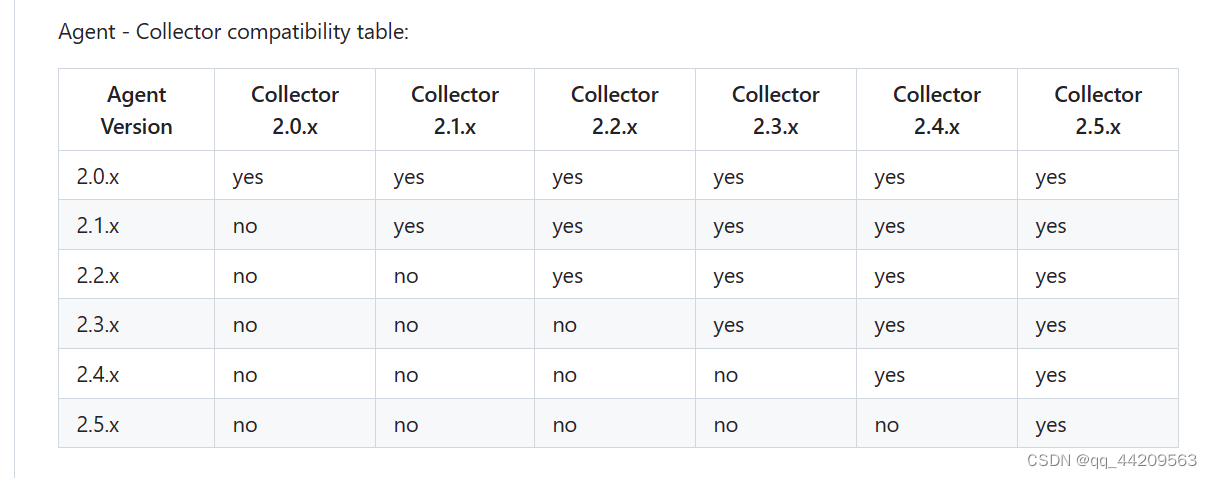
pinpoint安装部署(相关博客合集)
pinpoint安装部署 说明一、PinPoint介绍及工作原理1.1 确定部署的组件及服务 二、相关组件版本兼容情况2.1 确定版本 三、部署3.1 HBASE3.2 agent 说明 本博客写在搭建PinPoint之前,主要是用来记录查阅的相关博客资料,等到动手搭建完再更新实际部署操作…...
)
python-匿名函数(lambda函数)
匿名函数(lambda函数) 匿名函数(也称为lambda函数)是一种在代码中定义临时函数的方式,它没有明确的函数名称。匿名函数通常用于需要简短、一次性的函数定义,特别是在处理函数作为参数传递或函数返回的情况…...

JS逆向常见情况
分类:JS压缩混淆加密 与 URL/API参数的加密 代码压缩:去除不必要的空格换行等内容,使源码变成几行,大大降低可读性并提升网站加载速度 代码混淆:使用变量替换、字符串阵列化、控制流平坦化、多态变异、僵尸函数…...

利用matlab对滤波器频率特性分析
【设计目标】对双二阶环路滤波器进行时频域分析和处理的基本方法 【设计工具】MATLAB【设计要求】 1)分析典型的双二阶环路滤波器电路:低通、高通、带通、带阻 2)理论分析各滤波电路的系统函数 3)利用Matlab分析各滤波电路的系统函数的频率特性(幅频、相频)、零极点分…...
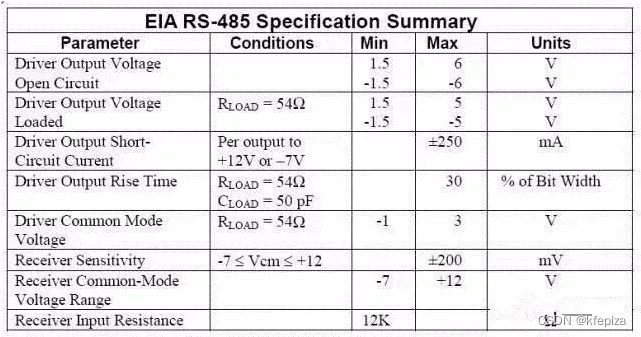
对比 RS232,RS422,RS485
对比 RS232,RS422,RS485 首先, 串口、UART口、COM口、RJ45网口、USB口是指的物理接口形式(硬件)。TTL、RS-232、RS-485、RS-422是指的电平标准(电信号)。 RS232,RS422,RS485 对比表格 通信标准RS-232RS-422RS-485工作方式单端差分差分通信线数量4 地线52 地线3节…...
python使用requests+excel进行接口自动化测试(建议收藏)
前言 在当今的互联网时代中,接口自动化测试越来越成为软件测试的重要组成部分。Python是一种简单易学,高效且可扩展的语言,自然而然地成为了开发人员的首选开发语言。而requests和xlwt这两个常用的Python标准库,能够帮助我们轻松…...

华为OD机试真题 Java 实现【食堂供餐】【2023 B卷 考生抽中题】,附详细解题思路
一、题目描述 某公司员工食堂以盒饭的方式供餐。 为将员工取餐排队时间降为0,食堂的供餐速度必须要足够快。 现在需要根据以往员工取餐的统计信息,计算出一个刚好能达到排队时间为0的最低供餐速度。 即,食堂在每个单位时间内必须至少做出多少份盒饭才能满足要求。 二、…...

一分钟学一个 Linux 命令 - cd
前言 大家好,我是 god23bin。欢迎来到这个系列,每天只需一分钟,记住一个 Linux 命令不成问题。今天让我们从 cd 命令开始,掌握在 Linux 系统中切换目录的技巧。 什么是 cd 命令? cd 命令来自这么一个词语࿰…...
常用命令汇总)
vi(vim)常用命令汇总
vim ~/.vimrc vim.vimrc 配置 set nobackup set cursorline #当前行 set cc100 #分屏线 set number set laststatus2 syntax on colorscheme delek 快速移动光标 w(e) 移动光标到下一个单词 b 移动光标到上一个单词 0 移动光标到本行最开头 ^ 移动光标到本行最开头的字符…...
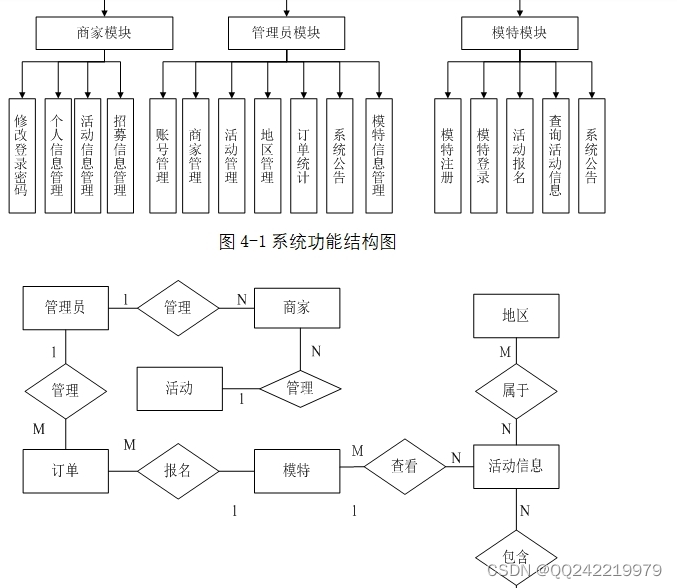
模特信息管理系统的开发与实现(ASP.NET,SQLServer)
需求分析 模特信息管理系统主要给商家和模特用户提供服务,系统分为前台和后台两部分。 本研究课题重点主要包括:活动管理,商家管理,模特管理,系统公告管理和活动报名管理。 活动管理模块主要实现活动更新、活动添加、活…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
