K8s运维备忘
1.服务器集群搭建:
VagrantFile中加入以下代码,创建3个虚拟机:
Vagrant.configure("2") do |config|
(1..3).each do |i|
config.vm.define "k8s-node#{i}" do |node|
# 设置虚拟机的Box
node.vm.box = "centos7"
config.vm.box_url = "https://mirrors.ustc.edu.cn/centos-cloud/centos/7/vagrant/x86_64/images/CentOS-7.box"
# 设置虚拟机的主机名
node.vm.hostname="k8s-node#{i}"
# 设置虚拟机的IP
node.vm.network "private_network", ip: "192.168.56.#{99+i}", netmask: "255.255.255.0"
# 设置主机与虚拟机的共享目录
# node.vm.synced_folder "~/Documents/vagrant/share", "/home/vagrant/share"
# VirtaulBox相关配置
node.vm.provider "virtualbox" do |v|
# 设置虚拟机的名称
v.name = "k8s-node#{i}"
# 设置虚拟机的内存大小
v.memory = 2048
# 设置虚拟机的CPU个数
v.cpus = 2
end
end
end
end
相关文章:

K8s运维备忘
1.服务器集群搭建: VagrantFile中加入以下代码,创建3个虚拟机: Vagrant.configure("2") do |config| (1..3).each do |i| config.vm.define "k8s-node#{i}" do |node| # 设置虚拟机的Box …...
)
激光雷达+rtk+rgb联合使用(4)
因为一直在忙一些乱七八糟的事情,就没顾得上继续写,想着快速收尾算了。 前面写到,我在点云的匹配上花了大量的时间,不断的调参数,换方法,一共几百个点云,想着先每50个匹配一次,得到几…...

【K8S系列】快速初始化⼀个最⼩集群
序言 走得最慢的人,只要不丧失目标,也比漫无目的地徘徊的人走得快。 文章标记颜色说明: 黄色:重要标题红色:用来标记结论绿色:用来标记一级重要蓝色:用来标记二级重要 希望这篇文章能让你不仅有…...
Exploit/CVE-2010-0738
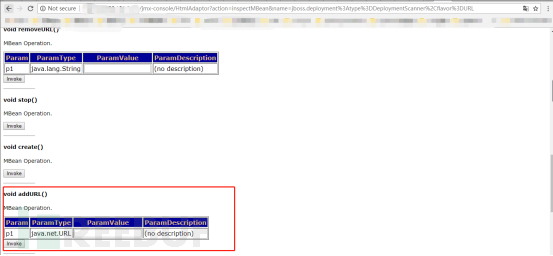
打开JBoss的潘多拉魔盒:JBoss高危漏洞分析 *本文中涉及到的相关漏洞已报送厂商并得到修复,本文仅限技术研究与讨论,严禁用于非法用途,否则产生的一切后果自行承担。 前言 JBoss是一个基于J2EE的开放源代码应用服务器࿰…...
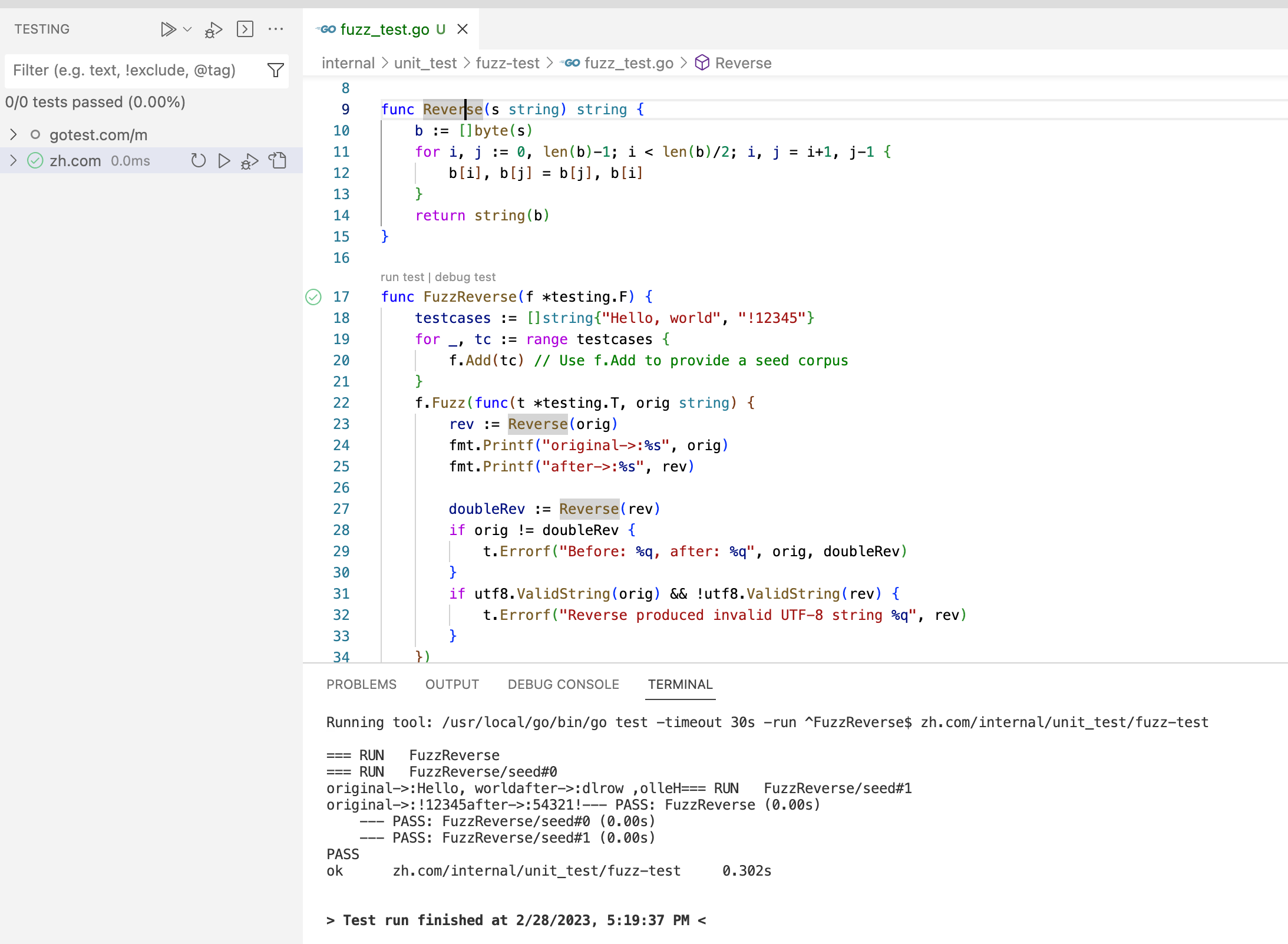
Go单元测试及框架使用
Go自带测试框架 单元测试 建议Go 语言推荐测试文件和源代码文件放在一块,测试文件以 _test.go 结尾。函数名必须以 Test 开头,后面一般跟待测试的函数名参数为 t *testing.T 简单测试用例定义如下: func TestXXXX(t *testing.T) {// ...}…...

TreeMap类型实体类数据进行排序
实体类Student类代码如下所示: package com.test.Test11;public class Student implements Comparable<Student>{private int age;private String name;private Double height;public int getAge() {return age;}public void setAge(int age) {this.age age…...
HOOPS助力AVEVA数字化转型:支持多种3D模型格式转换!
行业: 电力和公用事业、化工、造船、能源、采矿业 挑战: 创建大规模复杂资产的客户需要汇集多种类型的数据,以支持初始设计和创建强大的数字双胞胎;现有版本的产品只支持半打CAD格式;有限的内部开发资源限制了增加对新…...
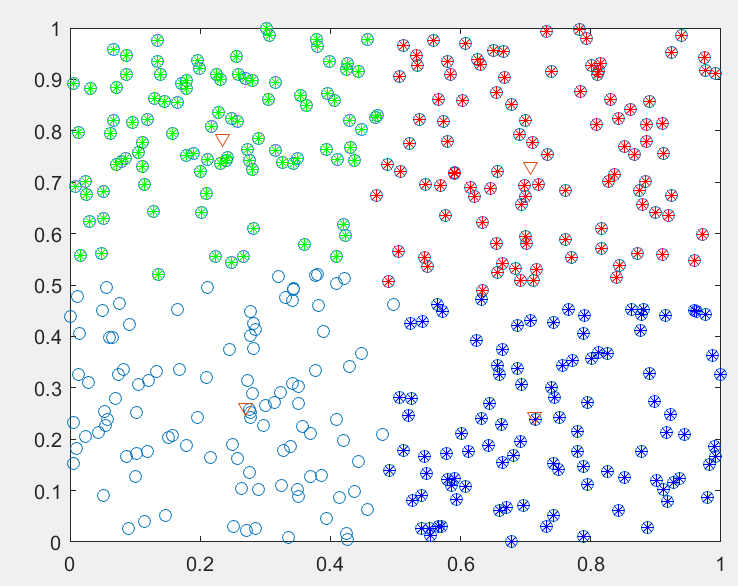
(转载)基于遗传模拟退火的聚类算法(matlab实现)
1 理论基础 1.1 模糊聚类分析 模糊聚类是目前知识发现以及模式识别等诸多领域中的重要研究分支之一。随着研究范围的拓展,不管是科学研究还是实际应用,都对聚类的结果从多方面提出了更高的要求。模糊C-均值聚类(FCM)是目前比较流行的一种聚类方法。该…...

【C++】struct 和 class 的区别
欢迎来到博主 Apeiron 的博客,祝您旅程愉快。时止则止,时行则行。动静不失其时,其道光明。 目录 1、缘起 2、示例代码 3、总结 1、缘起 在 C 中,struct 和 class 唯一的区别就在于 默认的访问权限不同。区别如下: …...
活动笔记丨物业行业人效提升与灵活用工新路径
近日,盖雅工场成功举办物业行业人效提升专场交流,来自广深地区央企和民营的领先物业企业和现场服务业的多位代表齐聚深圳招商积余大厦,共同研讨行业人效提升的挑战和实践。 本次闭门交流会聚焦于人效提升,讨论话题包括各自企业在人…...
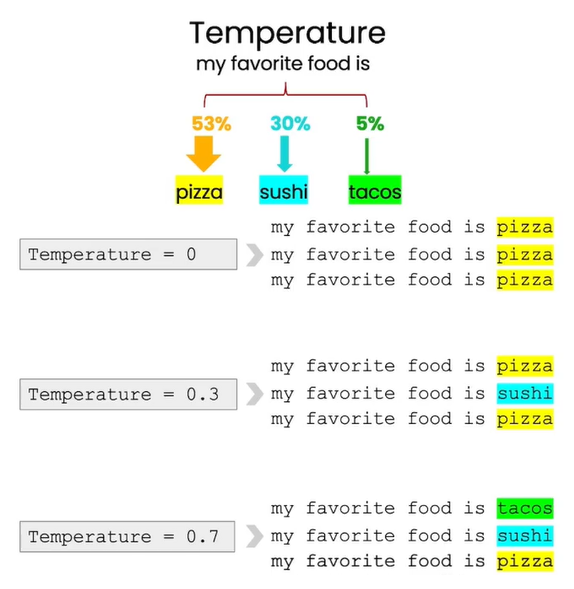
学习笔记:吴恩达ChatGPT提示工程
以下为个人笔记,原课程网址Short Courses | Learn Generative AI from DeepLearning.AI 01 Introduction 1.1 基础LLM 输入 从前有一只独角兽,输出 它和其他独角兽朋友一起住在森林里输入 法国的首都在哪?输出 法国的首都在哪…...
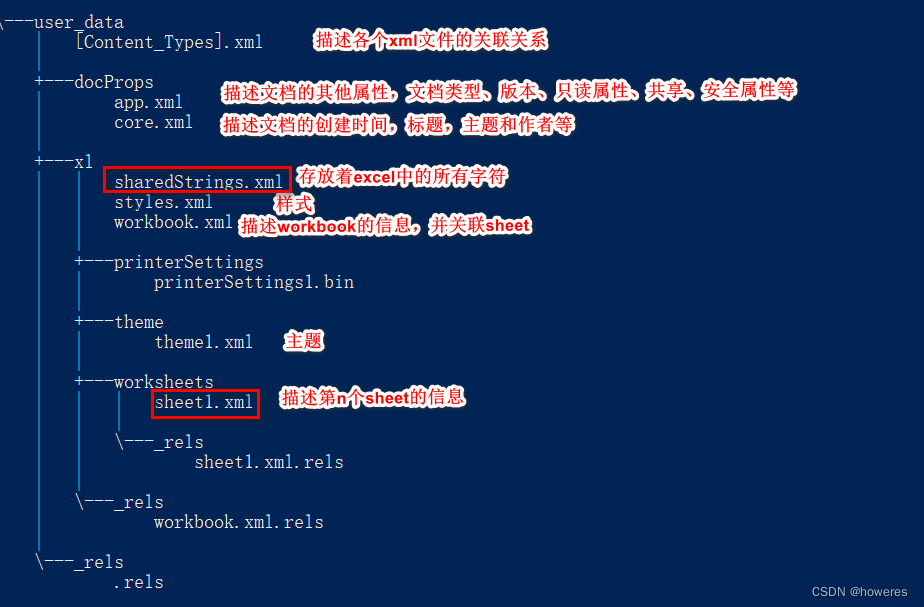
POI in Action
POI 组件依赖 按需引入对应依赖 (给出官方的指引) 组件作用Maven依赖POIFSOLE2 FilesystempoiHPSFOLE2 Property SetspoiHSSFExcel XLSpoiHSLFPowerPoint PPTpoi-scratchpadHWPFWord DOCpoi-scratchpadHDGFVisio VSDpoi-scratchpadHPBFPublisher PUBpoi-scratchpadHSMFOutloo…...

苹果Vision Pro将引爆人机交互的重大变革
2023年6月6日,苹果发布了大家期待已久的Vision Pro,Vision Pro是一款专业级MR设备,融合了虚拟现实(VR)和增强现实(AR)技术,可以让用户完全沉浸在高分辨率显示内容中。允许用户以一种全新的方式在其周围的空间中查看APP。用户可以用…...
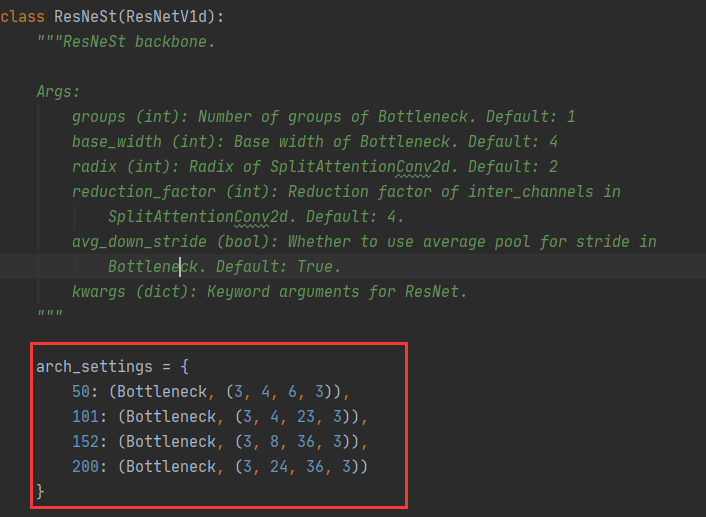
MMDetection学习记录(二)之配置文件
文件结构 config文件 在 config_base_ 文件夹下有 4 个基本组件类型,分别是:数据集(dataset),模型(model),训练策略(schedule)和运行时的默认设置(default runtime)。 命名风格 {model}_[model setting]_{backbone}_{neck}_[no…...

Python数据分析:NumPy、Pandas和Matplotlib的使用和实践
在现代数据分析领域中,Python已成为最受欢迎的编程语言之一。Python通过庞大的社区和出色的库支持,成为了数据科学家和分析师的首选语言。在Python的库中,NumPy、Pandas和Matplotlib是三个最为重要的库,它们分别用于处理数值数组、…...

实习生面试问题及回答记录
文章目录 文章简介技术类1、DFS和BFS算法的区别是什么?2、解释一下什么是快速排序?3、 如果让你写一个排序算法?你会怎么写?(大概说出代码的思路)4、解释一下二分查找的具体逻辑?5、在代码的数据…...
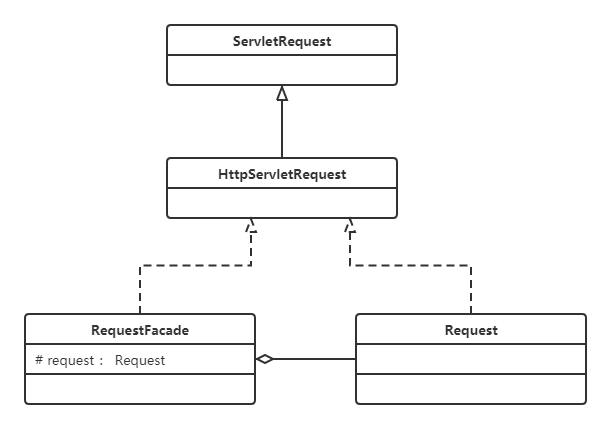
设计模式(十):结构型之外观模式
设计模式系列文章 设计模式(一):创建型之单例模式 设计模式(二、三):创建型之工厂方法和抽象工厂模式 设计模式(四):创建型之原型模式 设计模式(五):创建型之建造者模式 设计模式(六):结构型之代理模式 设计模式…...

买法拍房需要注意什么
法拍房,由于其价格亲民、房屋信息透明度高、竞拍过程公平公正而受到越来越多的人开始关注。但是其中又有着许多的风险及相关的注意事项。那么,如何做到成功“捡漏”,买法拍房需要注意什么呢? 买法拍房需要注意什么 1、隐藏的各种收费 税费&a…...

linux命令输出结果但不显示在屏幕上的通用办法
linux命令输出结果但不显示在屏幕上的通用办法 这个针对于我这种小白马大哈很简单的一个命令,记给自己备用 举个例子:unzip命令不输出结果 unzip xx.zip > /dev/null 2>&1 unzip xx.zip > /dev/null 前半部分是将标准输出重定向到空设备&a…...

【Linux系统进阶详解】Linux字符权限rwx-权限组合原理,对应类型ugo,user,group,other,+-=详解及权限管理实战
在Linux系统中,每个文件和目录都有三种权限:读权限(r)、写权限(w)和执行权限(x)。这些权限可以被分配给三个不同的用户组:用户(user)、组(group)和其他人(other)。此外,权限可以使用“+”、“-”和“=”符号进行修改。 权限组合原理 Linux系统中的权限由字母…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
