【改进的多同步挤压变换】基于改进多同步挤压的高分辨率时频分析工具,用于分析非平稳信号(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码、数据、文章
💥1 概述
文献来源:

该文提出一种高分辨率时频(TF)分析方法,用于强非平稳信号的分析。通过传统方法生成的TF表示通常过于模糊,无法为此类信号提供精确的特征。最近提出的一种称为多同步挤压变换(MSST)的方法克服了传统方法中存在的大多数问题,这似乎是一种很有前途的工具。但是,MSST仍然存在一个主要问题,即非重分配点问题,这可能导致一些特殊TF点的能量模糊问题。本文主要关注解决这个问题。研究发现,MSST中的此类问题是由重分配步骤的离散过程中的舍入操作引起的。然后采用一种有效的方法来使用简单的策略来解决这个问题。此外,研究中还提供了离散实现。数值分析表明,所提方法能够有效提高与MSST相当的能量浓度。与其他先进方法的比较还表明,所提出的方法在处理强非平稳信号和噪声附加信号方面具有更好的性能。在实验信号分析中,我们进行了三个实验,以验证所提方法在真实世界信号分析中的有效性。
原文摘要:
In this paper, a high-resolution time-frequency (TF) analysis method is presented for the analysis of strongly non-stationary signals. TF representations generated by conventional methods are usually too blurry to provide precise features for such signals. A recently proposed method, called multisynchrosqueezing transform (MSST), overcomes most of the problems that exist in conventional methods, which seems to be a promising tool. However, the MSST still has a major problem, i.e., non-reassigned point problem, which may lead to the blurry energy problem for some special TF points. This paper mainly focuses on resolving this problem. This study finds that such a problem in the MSST is caused by the rounding operation in the discrete procedure of the reassigned step. An effective method is then employed to address this problem using a simple strategy. Additionally, discrete implementation is provided in the study. The numerical analysis shows that our proposed method can effectively improve the energy concentration comparable to the MSST. Comparisons with other advanced methods also show that the proposed method offers better performance in addressing strongly non-stationary signals and noise-added signals. In the experimental signal analysis, we carry out three experiments to validate the effectiveness of the proposed method in the analysis of real-world signals.
有轴承缺陷的旋转机器通常会产生脉冲信号,振动传感器[1],[2],[3],[4],[5],[6],[7]。然而,当机器以可变速度运行时,振动信号处理变得具有挑战性。这是因为在这种情况下测量的信号通常表现出强烈的非平稳特性,即信号的频率随时间而变化很大。非平稳信号分析在旋转机械故障诊断中越来越受到关注。时频(TF)分析(TFA)技术具有应对此类挑战的强大能力。回顾TFA技术在旋转机械故障诊断中的发展的几篇文章可以在[8],[9],[10]中找到。从最近的研究中可以知道,能量浓度是评估TFA方法性能的关键指标[11]。这是因为集中TF表示(TFR)具有更好的表征信号故障特征的能力。然而,受海森堡不确定性原理的限制,传统的TFA方法,例如短时傅里叶变换(STFT),小波变换(WT)和S变换,在处理强时变信号时难以提供集中的结果。近几十年来,旨在克服传统方法缺点的各种新开发的TFA技术引起了广泛关注,例如,重新分配方法(RM)[12],同步挤压变换(SST)[13,14],解调SST(DSST)[15,16],高阶SST [17],[18],[19],同步提取变换(SET)[20,21]和多SST(MSST)[22]。
RM技术旨在根据信号的瞬时频率(IF)和群延迟的局部估计,将数据映射到更接近集中区域的新坐标[12],从而锐化能量涂抹的TFR。这种能量涂抹的TFR通常是由STFT,WT或S变换预先产生的。但是,RM 的映射应用于频谱图或标度图,通常定义为 STFT 或 WT 的平方幅度。这样的映射会丢失信号的相位信息,这也意味着无法从RM结果重建信号。作为一种类似RM的后处理技术,SST仅根据IF的估计值执行TFR映射,从而保留了逆能力。这使得SST在许多领域更具优势,例如机械故障诊断[23,24],地震信号分析[25,26]和呼吸动力学分析[27]。最近的各种研究侧重于在表征强时变信号时进一步增强SST技术的能力[13],[14],[15],[16],[17],[18],[19],[20],[21],[22]。
在线性TFA算法框架下提出了SST技术,例如WT,STFT和S变换。然而,受线性TF原子缺点的限制,线性TFA方法不能很好地处理强时变信号。相应的TF结果经常受到能量模糊问题的困扰。SST也面临同样的问题。解调技术设计非线性TF原子来表征时变信号,可以有效克服线性TFA方法的问题。此外,基于解调技术的新型SST方法在提高能量浓度方面显示出广阔的潜力。这种技术通常称为DSST方法[15,16]。然而,解调技术必须根据信号的先验信息设计非线性TF原子[9]。在实践中,很难甚至不可能提前确定真实世界信号的基本信息。这阻碍了DSST技术的工程应用。
提出了高阶SST方法来处理高度调频(FM)信号,该方法不需要事先提供有关信号的任何信息[17],[18],[19]。理论上,SST假设分析的信号应该是纯谐波信号。这意味着 SST 仅适用于处理微弱的 FM 信号。为了改善这种情况,在更复杂的信号模型上建立了高阶SST的框架,例如线性FM信号和高阶多项式FM信号。在无噪声情况下,高阶SST可以为强时变信号提供高度集中的结果。然而,最近的研究发现,高阶SST方法对噪声非常敏感。使用这种方法通常很难获得具有高噪声的信号的满意结果[22]。
SET方法旨在仅保留与信号时变特征密切相关的TF系数[20,21]。此外,SET消除了大多数弱相关的TF系数。因此,SET结果比SST结果更集中。但是,SET仅提供信号的近似重建。重建的性能随着信号非线性度的增加而降低。
最近发表的一篇论文介绍了MSST方法,该方法采用迭代程序来提高SST的能量浓度。MSST允许对信号进行完美的重建,不需要先验信息。[22]中的研究表明,在处理无噪声和加噪声信号时,MSST可以提供比RM,DSST和高阶SST更集中的结果。MSST方法似乎是实现理想TFR(ITFR)的有前途的工具[28]。然而,[22]的讨论部分指出,MSST方法中存在一个主要问题,即阻碍TF特征集中表征的非重分配点问题。
📚2 运行结果

 部分代码:
部分代码:
function [Ts] = IMSST_Z(x,hlength,num)
% Computes the IMSST (Ts) of the signal x.
% INPUT
% x : Signal needed to be column vector.
% hlength: The length of window function.
% num : iteration number.
% OUTPUT
% Ts : The SST
% tfr : The STFT
[xrow,xcol] = size(x);
if (xcol~=1),
error('X must be column vector');
end;
if (nargin == 2),
num=10;
end
if (nargin == 1),
num=10;
hlength=xrow/8;
end
hlength=hlength+1-rem(hlength,2);
ht = linspace(-0.5,0.5,hlength);ht=ht';
% Gaussian window
h = exp(-pi/0.32^2*ht.^2);
[hrow,~]=size(h); Lh=(hrow-1)/2;
N=xrow;
t=1:xrow;
tfr= zeros (round(N/2),N) ;
omega = zeros (round(N/2),N-1);
omega2 = zeros (round(N/2),N);
Ts = zeros (round(N/2),N);
%Compute STFT
for icol=1:N,
ti= t(icol); tau=-min([round(N/2)-1,Lh,ti-1]):min([round(N/2)-1,Lh,xrow-ti]);
indices= rem(N+tau,N)+1;
rSig = x(ti+tau,1);
tfr(indices,icol)=rSig.*conj(h(Lh+1+tau));
end;
tfr=fft(tfr);
tfr=tfr(1:round(N/2),:);
%2D IF of the SST
for i=1:round(N/2)
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。

🌈4 Matlab代码、数据、文章
相关文章:

【改进的多同步挤压变换】基于改进多同步挤压的高分辨率时频分析工具,用于分析非平稳信号(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

有关 python 切片的趣事
哈喽大家好,我是咸鱼 今天来讲一个我在实现 python 列表切片时遇到的趣事 在正式开始之前,我们先来了解一下切片(slice) 切片操作是访问序列(列表、字符串…)中元素的另一种方法,它可以访问一…...

ChatGPT 会带来失业潮吗?
(永久免费,扫码加入) 最近在翻知乎上的一些文章,很多都是跟ChatGPT有关的。因为本身是搞Python编程的,知乎推荐系统给我推荐了一篇廖雪峰老师的文章,觉得很有意思。 一共1119个赞,还是很厉害的&…...

如何对待工作中的失误
在日复一日的工作中,我们免不了会产生一些失误,会因此感到沮丧和失望。但如何正确地对待和处理这些失误才是最重要的,它直接影响到我们的工作表现和个人成长。一起来谈谈作为职场人的你时如何处理工作中的失误的吧! 一、在面对失…...

微信小程序快速入门【一】
微信小程序快速入门【一】 文章目录 微信小程序快速入门【一】👨🏫内容1:背景👨⚖️内容2:准备工作👨💻内容3:新建一个小程序🍉文末推荐 👨…...
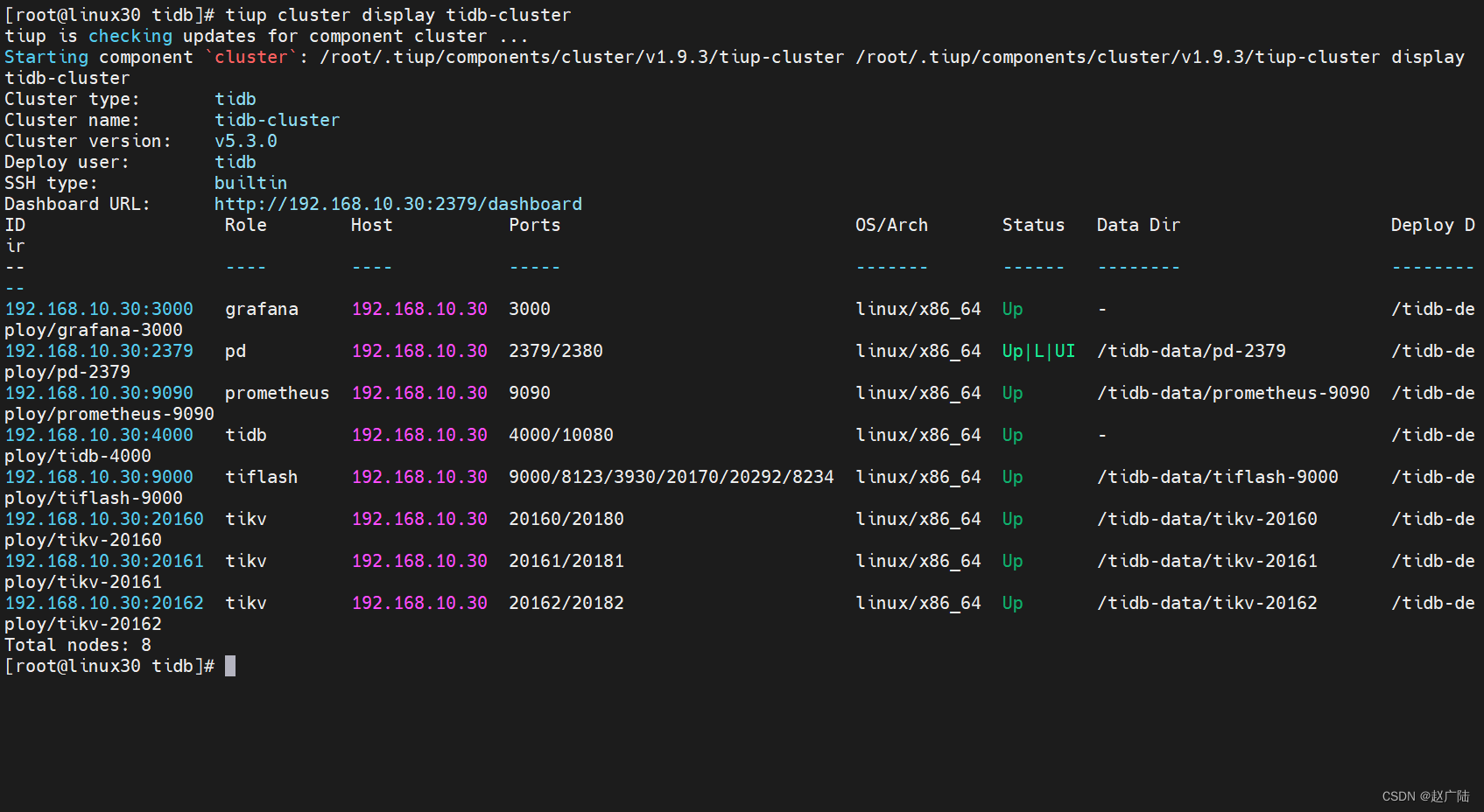
TiDB亿级数据亚秒响应查询集群部署
目录 1 集群部署1.1 环境要求1.1.1 操作系统建议配置1.1.2 服务器建议配置 1.2 环境准备1.3 安装TiUP1.3.1 什么是TiUP1.3.2 安装TiUP组件1.3.3 配置TiUP环境1.3.4 检查TiUP 工具是否安装1.3.5 安装 cluster 组件1.3.6 升级cluster组件 1.4 编辑部署文件1.4.1 常见的部署场景1.…...

并发——同步访问共享的可变数据
关键字 synchronized 可以保证在同一时刻,只有一个线程可以执行某一个方法,或者某一段代码块。许多程序员把同步的概念仅仅理解为一种互斥的方式。即,当一个对象被一个线程修改的时候,可以阻止另一个线程观察到内部不一致的状态。…...
禁用容器网络)
Docker网络模型(九)禁用容器网络
禁用容器网络 如果你想完全禁用容器上的协议栈,你可以在启动容器时使用 --network none 标志。在容器内,只有回环设备被创建。下面的例子说明了这一点。 创建容器 $ docker run --rm -dit \--network none \--name no-net-alpine \alpine:latest \ash通…...

JavaScript 教程---互联网文档计划
学习目标: 每天记录一章笔记 学习内容: JavaScript 教程---互联网文档计划 笔记时间: 2023-6-5 --- 2023-6-11 学习产出: 1.入门篇 1、JavaScript 的核心语法包含部分 基本语法标准库宿主API 基本语法:比如操作符…...

做好功能测试需要的8项基本技能【点工进来】
功能测试是测试工程师的基础功,很多人功能测试还做不好,就想去做性能测试、自动化测试。很多人对功能测试的理解就是点点点,如何自己不用心去悟,去研究,那么你的职业生涯也就停留在点点点上了。在这里,我把…...
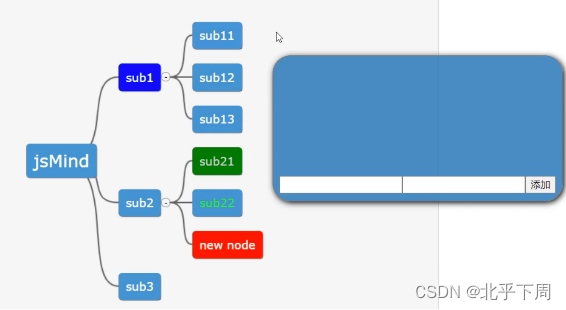
在弹出框内三个元素做水平显示
最终效果图要求是这样: js代码: // 显示弹出窗口 function showPopup(node) {var popup document.createElement(div);popup.className popup;var inputContainer1 document.createElement(div);/* inputContainer1.className input-container1; */…...

纠删码技术在vivo存储系统的演进【上篇】
作者:vivo 互联网服务器团队- Gong Bing 本文将学术界和工业界的纠删码技术的核心研究成果进行了相应的梳理,然后针对公司线上存储系统的纠删码进行分析,结合互联网企业通用的IDC资源、服务器资源、网络资源、业务特性进行分析对原有纠删码技…...
如何实现APP自动化测试?
APP测试,尤其是APP的自动化测试,在软件测试工程师的面试中越来越会被问到了。为了更好的回答这个问题,我今天就给大家分享一下,如何进行APP的自动化测试。 一、为了实现JavaAppiumJunit技术用于APP自动化测试,所以需要…...

INNODB和MyISAM区别
1 存储引擎是MyISAM 如下: CREATE table test_myisam (cli int ) ENGINEMyISAM 存储目录里会有三个文件 test_myisam.frm为“表定义”,是描述数据表结构的文件 test_myisam.MYI文件是表的索引 test_myisam.MYD文件是表的数据 2 存储引擎是INNODB…...
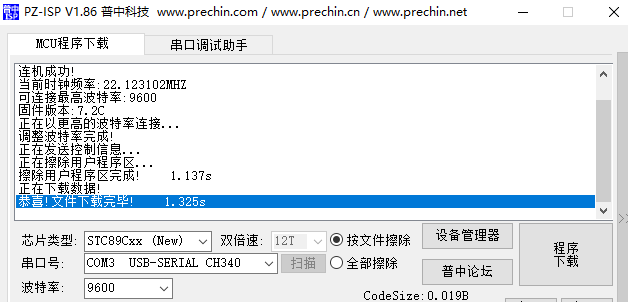
普中自动下载软件1.86下载程序失败案例
今天在用开发板做一个功能,下载的时候报错了,说芯片超时 确定驱动安装好了的 波特率也试了一圈 线也换过了 最后发现是芯片类型选错了,这个开发板是用的stc89c52,所以我选了图里这个,但是翻了开发板配套的资料,发现…...

JavaScript HTML DOM
JavaScript HTML DOM(文档对象模型)是一种用于访问和操作HTML文档元素的编程接口。它将HTML文档表示为一个树形结构,使开发人员可以使用JavaScript来操作和修改HTML元素、属性、样式和事件。 通过使用HTML DOM,你可以使用JavaScr…...
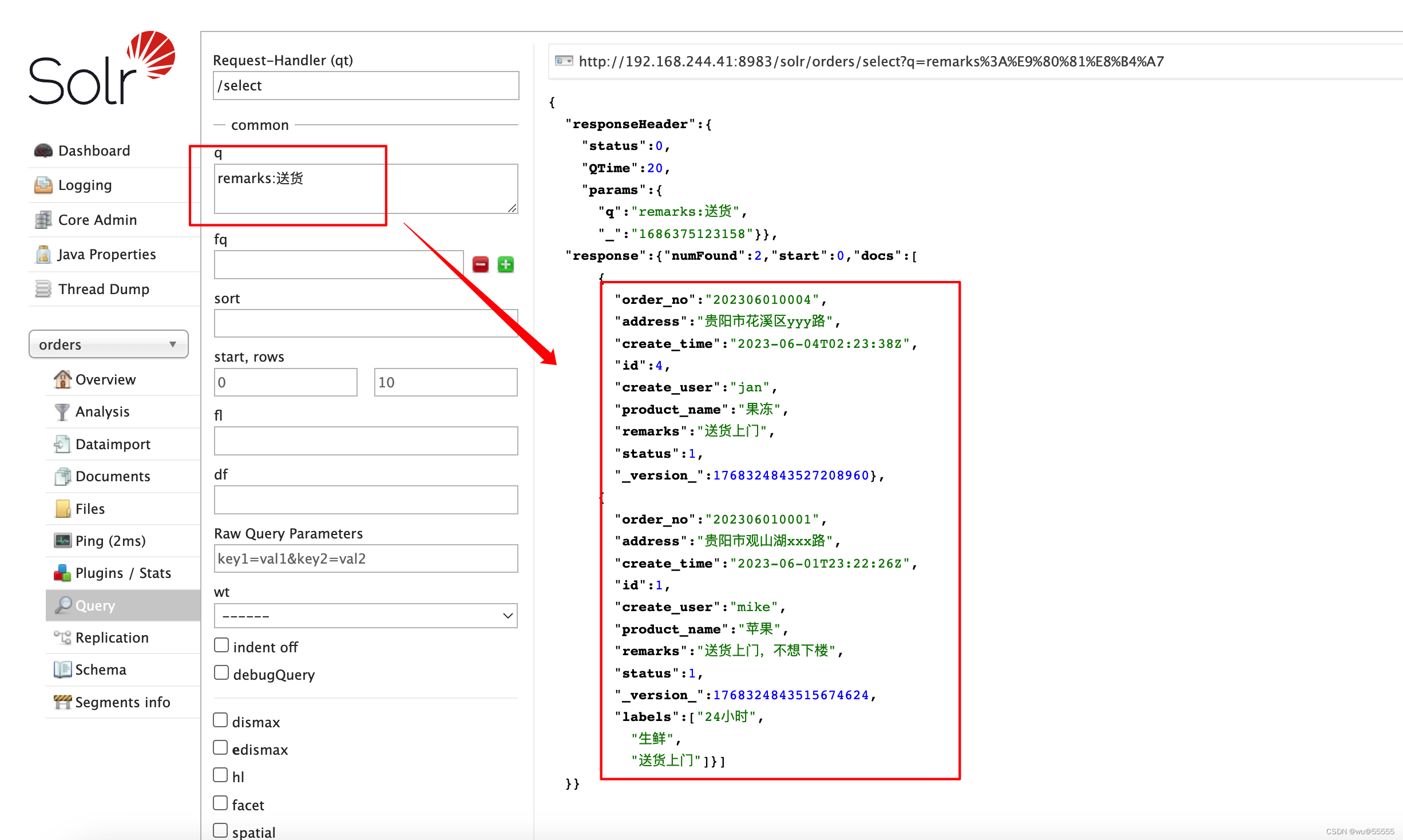
solr快速上手:配置IK中文分词器(七)
0. 引言 solr作为搜索引擎,常用在我们对于搜索速度有较高要求且大数据量的业务场景,我们之前已经配置过英文分词器,但是针对中文分词不够灵活和实用,要实现真正意义上的中文分词,还需要单独安装中文分词器 solr快速上…...

【软件测试】接口测试工具APIpost
说实话,了解APIpost是因为,我的所有接口相关的文章下,都有该APIpost水军的评论,无非就是APIpost是中文版的postman,有多么多么好用,虽然咱也还不是什么啥网红,但是不知会一声就乱在评论区打广告…...

第六章 假言:那么、就、则;才。
第六章 假言:那么、就、则;才。 第一节 假言-公式化转换-等价矛盾 真题(2012-38)-假言-A→B的公式化转换-A→B的等价命题:①逆否命题:非B→非A。 38.经理说:“有了自信不一定赢。”董事长回…...

[干货] 如何解决慢SQL?详细分析和优化实践!
慢SQL优化实践 本篇博客将分享如何通过慢SQL分析工具和常用优化手段,来解决慢SQL的问题。首先让我们看一下慢SQL的定义。 什么是慢SQL 简单来说,慢SQL指的是执行时间较长的SQL语句。在数据库中,一个查询的运行时间往往会受到多种因素的影响…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

