【机器学习】采样方法
文章目录
- 采样方法
- 11.1 简介
- 11.2 常见采样方法
- 11.2.1 均匀分布采样
- 11.2.2 逆变换采样
- 11.2.3 拒绝采样
- 11.2.4 重要采样
- 11.2.5 Metropolis方法
- 11.2.6 Metropolis-Hasting 算法
- 11.2.7 吉布斯采样
采样方法
11.1 简介
-
什么是采样
从一个分布中生成一批服从该分布的样本,该过程叫采样.采样本质上是对随机现象的模拟,根据给定的概率分布,来模拟产生一个对应的随机事件。采样可以让人们对随机事件及其产生过程有更直观的认识.
-
蒙特卡洛
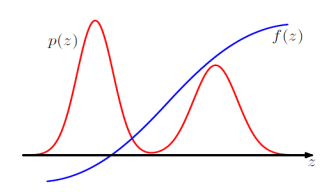
要解决的问题:寻找某个定义在概率分布𝑝(𝑧)上的函数𝑓(𝑧)的期望,即计算 E ( f ) = ∫ f ( z ) p ( z ) d z \mathbb E(f)=\int f(\mathbf z)p(\mathbf z)\mathrm d\mathbf z E(f)=∫f(z)p(z)dz
对于大多数实际应用中的概率模型来说,无法精确计算其和或积分,可以采取基于数值采样的近似推断方法,也被称为蒙特卡罗(MonteCarlo)方法
对这个问题,蒙特卡罗方法是从概率分布𝑝(𝑧)中独立抽取𝑙个样本 z ( 1 ) , z ( 2 ) , . . . , z ( l ) z^{(1)},z^{(2)},...,z^{(l)} z(1),z(2),...,z(l) ,这样期望即可通过有限和的方式计算,以此得到一个经验平均值,即计算: f ^ = 1 L ∑ l = 1 L f ( z ( l ) ) \hat{f}=\frac{1}{L}\sum_{l=1}^{L}f\bigl(\mathbf{z}^{(l)}\bigr) f^=L1∑l=1Lf(z(l))
11.2 常见采样方法
11.2.1 均匀分布采样
均匀分布是指整个样本空间中的每一个样本点对应的概率(密度)都是相等的;根据样本空间是否连续,又分为离散均匀分布和连续均匀分布。
一般计算机的程序都是确定性的,无法产生真正意义上的完全均匀分布的随机数,只能产生伪随机数,用线性同余法生成区间[0, m - 1]上的伪随机数序列:
x t + 1 = ( a ⋅ x t + c ) m o d m x_{t+1}=(a\cdot x_t+c)\mod m xt+1=(a⋅xt+c)modm
其中,模 m > 0 m>0 m>0,系数 0 < a < m 0<a<m 0<a<m,增量 0 ≤ c < m 0\leq c<m 0≤c<m,种子 x 0 x_0 x0满足 0 ≤ x 0 < m 0\leq x_{0}<m 0≤x0<m

11.2.2 逆变换采样
定理:设𝑦是一个连续随机变量,概率密度函数为𝑝(𝑦) ,累计分布函数为ℎ(y) =P(𝑦) ,则𝑧 = ℎ(y) 是定义在区间0 ≤ 𝑧 ≤ 1上的均匀分布,即𝑝 (𝑧) = 1 (0 ≤ 𝑧 ≤ 1)。
证明:ℎ(y) 是累计分布函数,则0 ≤ 𝑧 = ℎ(y) ≤ 1,且ℎ(y)是单调递增函数 , z的累积分布函数:
P ( z ≤ Z ) = P ( h ( y ) ≤ Z ) = P ( y ≤ h − 1 ( Z ) ) = h ( h − 1 ( Z ) ) = Z p ( z ) = d F ( Z ) d Z = 1 ( 0 ≤ z ≤ 1 ) \begin{array}{c}\mathrm P(z\leq Z)=\mathrm P(h(y)\leq Z)=\mathrm P(y\leq h^{-1}(Z))=h(h^{-1}(Z))=Z\\\\ p(z)=\dfrac{\mathrm dF(Z)}{\mathrm dZ}=1(0\leq z\leq1)\end{array} P(z≤Z)=P(h(y)≤Z)=P(y≤h−1(Z))=h(h−1(Z))=Zp(z)=dZdF(Z)=1(0≤z≤1)
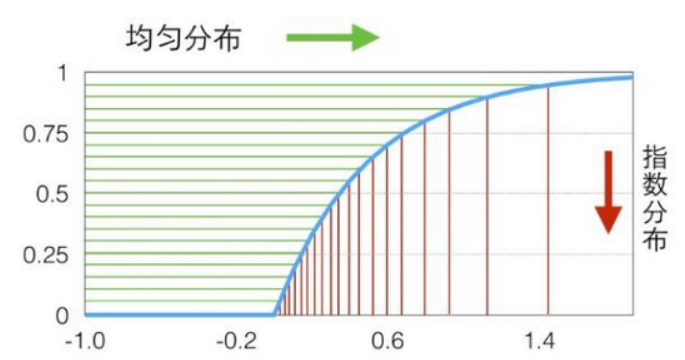
待采样的目标分布为 p ( x ) p(x) p(x),它的累计分布函数为 z = Φ ( X ) = ∫ − ∞ X p ( x ) d x \mathrm{z}=\Phi(X)=\int_{-\infty}^{X}p(x)d x z=Φ(X)=∫−∞Xp(x)dx,则逆变换采样法步骤为:
- 从均匀分布U(0,1)产生一个随机数 z i z_i zi
- 计算逆函数 X i = Φ − 1 ( z i ) X_{i}=\Phi^{-1}(z_{i}) Xi=Φ−1(zi),循环上述步骤,产生更多样本
例:
指数分布密度函数 p ( x ) = λ exp ( − λ x ) ( 0 ≤ x < ∞ ) p(x)=\lambda\exp(-\lambda x)(0\le x<\infty) p(x)=λexp(−λx)(0≤x<∞)其累计分布函数为 z = Φ ( X ) = 1 − exp ( − λ X ) \text{z}=\Phi(X)=1-\exp(-\lambda X) z=Φ(X)=1−exp(−λX)
其逆变换为: X = − λ − 1 ln ( 1 − z ) X=-\lambda^{-1}\ln(1-z) X=−λ−1ln(1−z)
11.2.3 拒绝采样
拒绝采样,又称为接受-拒绝采样,基本思想是用一“更大的的概率分布”或“更简单的概率分布”q(z)覆盖原本的概率分布,这个更简单的概率分布容易采样 (如正态分布)
- p ( z ) = 1 z p p ~ ( z ) \operatorname{p}(z)=\frac{1}{z_p}\tilde{\operatorname{p}}(z) p(z)=zp1p~(z)为采样分布, p ~ ( z ) \tilde{\operatorname{p}}(z) p~(z)为已知分布, Z p Z_p Zp为归一化因子(这一步没看明白暂且当成一样的)
- 引入较简单分布 q ( z ) q(z) q(z) ,称为提议分布,从中可以较容易采样
- 引入常数k,对任意z满足 k q ( z ) ≥ p ~ ( z ) \mathrm{kq}(z)\geq\tilde{\mathrm{p}}(z) kq(z)≥p~(z), k q ( z ) kq(z) kq(z)称为比较函数
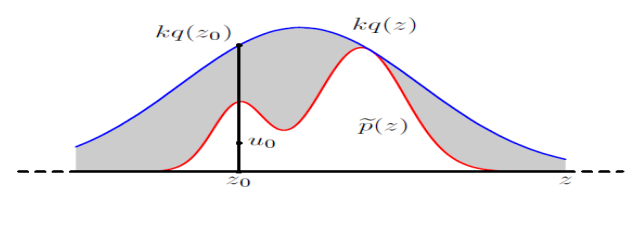
拒绝采样方法的步骤:
- 从 q ( z ) q(z) q(z)中随机采一个样本 z 0 z_0 z0
- 生成区间 [ 0 , k q ( z 0 ) ] [0,kq(z_0)] [0,kq(z0)]上的均匀分布的一个样本 u 0 u_0 u0
- 如果 u 0 ≥ p ~ ( z ) u_0\geq \tilde{\mathrm{p}}(z) u0≥p~(z),则拒绝该样本;反之接受
- 重复以上过程得到 [ z 0 , z 1 , … z n ] \left[z_{0},z_{1},\ldots z_{n}\right] [z0,z1,…zn]即是对 p ( z ) p(z) p(z)的一个近似
在上述拒绝采样方法中,𝑧的原始值从概率分布𝑞(𝑧)中生成,这些样本之后被接受的可能性为: p ~ ( z ) k q ( z ) \frac{{\tilde{p}}(z)}{k q(z)} kq(z)p~(z),因此,样本被接受的平均概率为:
p ( a c c e p t ) = ∫ { p ~ ( z ) k q ( z ) } q ( z ) d z = 1 k ∫ p ~ ( z ) d z p(\mathrm{accept})=\int\left\{\frac{\tilde{p}(z)}{kq(z)}\right\}q(z)dz=\frac{1}{k}\int\tilde{p}(z)dz p(accept)=∫{kq(z)p~(z)}q(z)dz=k1∫p~(z)dz
原则上𝑘可以取得很大,从而满足总能全覆盖,但是不难发现,𝑘取得越大,拒绝概率也更高;因此,选取的𝑘要尽可能的小,并使得𝑘𝑞(𝑧)恰好能覆盖$ \tilde{\mathrm{p}}(z)$
11.2.4 重要采样
E [ f ] = ∫ f ( z ) p ( z ) d z (11.1) \mathbb{E}[f] = \int f(z)p(z)dz \tag{11.1} \\ E[f]=∫f(z)p(z)dz(11.1)
f ^ = 1 L ∑ l = 1 L f ( z ( l ) ) (11.2) \hat{f} = \frac{1}{L}\sum\limits_{l=1}^L f(z^{(l)}) \tag{11.2} f^=L1l=1∑Lf(z(l))(11.2)
想从复杂概率分布中采样的一个主要原因是能够使用式(11.1)计算期望。重要采样(importance sampling)的方法提供了直接近似期望的框架,但是它本身并没有提供从概率分布$ p(z) $中采样的方法。
公式(11.2)给出的期望的有限和近似依赖于能够从概率分布 p ( z ) p(z) p(z)中采样。然而,假设直接从 p ( z ) p(z) p(z)中采样无法完成,但是对于任意给定的 z z z值,我们可以很容易地计算 p ( z ) p(z) p(z)。一种简单的计算期望的方法是将 z z z空间离散化为均匀的格点,将被积函数使用求和的方式计算,形式为
E [ f ] ≃ ∑ l = 1 L p ( z ( l ) ) f ( z ( l ) ) \mathbb{E}[f] \simeq \sum\limits_{l=1}^Lp(z^{(l)})f(z^{(l)}) E[f]≃l=1∑Lp(z(l))f(z(l))
这种方法的一个明显的问题是求和式中的项的数量随着 z z z的维度指数增长。此外,正如我们已经注意到的那样,我们感兴趣的概率分布通常将它们的大部分质量限制在 z z z空间的一个很小的区域,因此均匀地采样非常低效,因为在高维的问题中,只有非常小的一部分样本会对求和式产生巨大的贡献。我们希望从 p ( z ) p(z) p(z)的值较大的区域中采样,或理想情况下,从 p ( z ) f ( z ) p(z)f(z) p(z)f(z)的值较大的区域中采样。
与拒绝采样的情形相同,重要采样基于的是对提议分布 q ( z ) q(z) q(z)的使用,我们很容易从提议分布中采样,如下图所示:
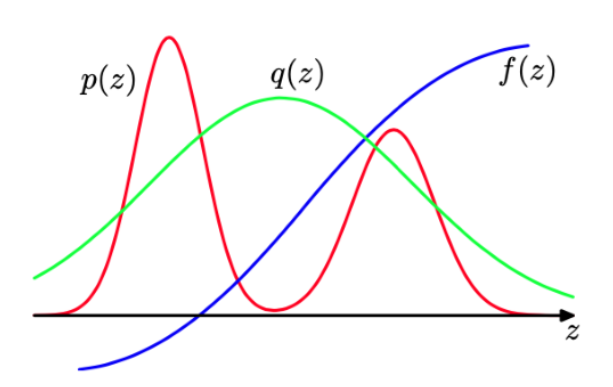
重要采样解决的是计算函数 f ( z ) f(z) f(z)关于分布 p ( z ) p(z) p(z)的期望的问题,其中,从 p ( z ) p(z) p(z)中直接采样比较困难。相反,样本 z ( l ) {z^{(l)}} z(l)从一个简单的概率分布 q ( z ) q(z) q(z)中抽取,求和式中的对应项的权值为 p ( z ( l ) ) / q ( z ( l ) ) p(z^{(l)})/q(z^{(l)}) p(z(l))/q(z(l)),这样就可以还原到从 p ( z ) p(z) p(z)中取样。
上述过程中的式子,我们可以通过$ q(z) 中的样本 中的样本 中的样本 {z^{(l)}} $的有限和的形式来表示期望
E = ∫ f ( z ) p ( z ) d z = ∫ f ( z ) p ( z ) q ( z ) q ( z ) d z ≃ 1 L ∑ l = 1 L p ( z ( l ) ) q ( z ( l ) ) f ( z ( l ) ) \mathbb{E} = \int f(z)p(z)dz \ = \int f(z)\frac{p(z)}{q(z)}q(z)dz \simeq \frac{1}{L}\sum\limits_{l=1}^L\frac{p(z^{(l)})}{q(z^{(l)})}f(z^{(l)}) E=∫f(z)p(z)dz =∫f(z)q(z)p(z)q(z)dz≃L1l=1∑Lq(z(l))p(z(l))f(z(l))
其中 r l = p ( z ( l ) ) / q ( z ( l ) ) r_l = p(z^{(l)}) / q(z^{(l)}) rl=p(z(l))/q(z(l))被称为重要性权重(importance weights),修正了由于从错误的概率分布 q ( z ) q(z) q(z)中采样引入的偏差。
而更常见的情形是,概率分布 p p p的计算结果没有标准化,也就是 p ( z ) = p ~ ( z ) / Z p p(z) = \tilde{p}(z) / Z_p p(z)=p~(z)/Zp中我们只知道 p ~ ( z ) \tilde{p}(z) p~(z),其中 p ~ ( z ) \tilde{p}(z) p~(z)可以很容易地由 z z z计算出来(可能没有函数表达式),而 Z p Z_p Zp未知( p ~ ( z ) \tilde{p}(z) p~(z)无法积分算)。类似的,我们可能希望使用重要采样分布 q ( z ) = q ~ ( z ) / Z q q(z) = \tilde{q}(z) / Z_q q(z)=q~(z)/Zq中的 q ~ ( z ) \tilde{q}(z) q~(z),它具有相同的性质。于是我们得到:
E [ f ] = ∫ f ( z ) p ( z ) d z = Z q Z p ∫ f ( z ) p ~ ( z ) q ~ ( z ) q ( z ) d z ≃ Z q Z p 1 L ∑ l = 1 L r ~ l f ( z ( l ) ) \mathbb{E}[f] = \int f(z)p(z)dz \ = \frac{Z_q}{Z_p}\int f(z)\frac{\tilde{p}(z)}{\tilde{q}(z)}q(z)dz \ \simeq \frac{Z_q}{Z_p}\frac{1}{L}\sum\limits_{l=1}^L\tilde{r}_lf(z^{(l)}) E[f]=∫f(z)p(z)dz =ZpZq∫f(z)q~(z)p~(z)q(z)dz ≃ZpZqL1l=1∑Lr~lf(z(l))
其中 r ~ l = p ~ ( z ( l ) ) / q ~ ( z ( l ) ) \tilde{r}_l = \tilde{p}(z^{(l)}) / \tilde{q}(z^{(l)}) r~l=p~(z(l))/q~(z(l))。
我们还可以使用同样的样本集合来计算比值 Z p / Z q Z_p / Z_q Zp/Zq,结果为:
Z p Z q = 1 Z q ∫ p ~ ( z ) d z = ∫ p ~ ( z ) q ~ ( z ) q ( z ) d z ≃ 1 L ∑ l = 1 L r ~ l \frac{Z_p}{Z_q} = \frac{1}{Z_q}\int\tilde{p}(z)dz = \int\frac{\tilde{p}(z)}{\tilde{q}(z)}q(z)dz \ \simeq \frac{1}{L}\sum\limits_{l=1}^L\tilde{r}_l ZqZp=Zq1∫p~(z)dz=∫q~(z)p~(z)q(z)dz ≃L1l=1∑Lr~l
第一个等式中 Z p Z_p Zp用 ∫ p ~ ( z ) d z \int\tilde{p}(z)dz ∫p~(z)dz等价计算了出来,第二个等式中 Z q Z_q Zq用 q ( z ) = q ~ ( z ) / Z q q(z) = \tilde{q}(z) / Z_q q(z)=q~(z)/Zq替代
因此:
E [ f ] ≃ ∑ l = 1 L w l f ( z ( l ) ) \mathbb{E}[f] \simeq \sum\limits_{l=1}^Lw_lf(z^{(l)}) E[f]≃l=1∑Lwlf(z(l))
其中:
w l = r ~ l ∑ m r ~ m = p ~ ( z ( l ) ) / q ( z ( l ) ) ∑ m p ~ ( z ( l ) ) / q ( z ( l ) ) w_l = \frac{\tilde{r}_l}{\sum_m\tilde{r}_m} = \frac{\tilde{p}(z^{(l)})/q(z^{(l)})}{\sum_m\tilde{p}(z^{(l)})/q(z^{(l)})} wl=∑mr~mr~l=∑mp~(z(l))/q(z(l))p~(z(l))/q(z(l))
11.2.5 Metropolis方法
与拒绝采样和重要采样相同,我们再一次从提议分布中采样。但是这次我们记录下当前状态 z ( τ ) z^{(\tau)} z(τ)以及依赖于这个当前状态的提议分布 q ( z ∣ z τ ) q(z|z^\tau) q(z∣zτ),从而样本序列 z ( 1 ) , z ( 2 ) , … z^{(1)},z^{(2)},\ldots z(1),z(2),…组成了一个马尔科夫链。
我们假设提议分布足够简单很容易直接采样,且 p ( z ) = p ~ ( z ) / Z p p(\mathbf{z})=\widetilde{p}({\mathbf{z}})/Z_{p} p(z)=p (z)/Zp中的 p ~ ( z ) \widetilde{p}({\mathbf{z}}) p (z)可以很容易的计算值。
在算法的每次迭代中,我们从提议分布中生成一个候选样本 z ∗ z^* z∗,然后根据一个恰当的准则接受这个样本。
在基本的 Metropolis 算法中,我们假定提议分布是对称的,即 q ( z A ∣ z B ) = q ( z B ∣ z A ) q(z_A|z_B)=q(z_B|z_A) q(zA∣zB)=q(zB∣zA)对于所有的 z A z_A zA和 z B z_B zB都成立。这样,候选样本被接受的概率为:
A ( z ⋆ , z ( τ ) ) = min ( 1 , p ~ ( z ⋆ ) p ~ ( z ( τ ) ) ) A(\mathbf{z}^{\star},\mathbf{z}^{(\tau)})=\min\left(1,\frac{\widetilde{p}(\mathbf{z}^{\star})}{\widetilde{p}(\mathbf{z}^{(\tau)})}\right) A(z⋆,z(τ))=min(1,p (z(τ))p (z⋆))
我们的接受准则是:当接受概率大于预设值u时,则接受这个样本。
如果候选样本被接受,那么 z ( τ + 1 ) = z ∗ z^{(\tau+1)} = z^* z(τ+1)=z∗;否则候选样本点 z ∗ z^* z∗被抛弃, z ( τ + 1 ) z^{(\tau+1)} z(τ+1)被设置为 z ( τ ) z^{(\tau)} z(τ)
然后从概率分布 q ( z ∣ z ( τ + 1 ) ) q(z|z^{(\tau+1)}) q(z∣z(τ+1))中再次抽取一个候选样本。
可以看到,在 Metropolis 算法中,当一个候选点被拒绝时,前一个样本点会被包含到是最终的样本的列表中,从而产生了这个样本点的多个副本。虽然在实际中我们只会保留一个样本副本,以及一个整数的权因子,记录状态出现了多少次。设计马尔科夫链蒙特卡洛方法的一个中心目标就是避免随机游走行为。

11.2.6 Metropolis-Hasting 算法
与 Metropolis 算法相比,提议分布不再是参数的一个对称函数,此时的接受概率变为:
A k ( z ⋆ , z ( τ ) ) = min ( 1 , p ~ ( z ⋆ ) q k ( z ( τ ) ∣ z ⋆ ) p ~ ( z ( τ ) ) q k ( z ⋆ ∣ z ( τ ) ) ) A_k(\mathbf{z}^{\star},\mathbf{z}^{(\tau)})=\min\left(1,\frac{\widetilde{p}(\mathbf{z}^{\star})q_k(\mathbf{z}^{(\tau)}|\mathbf{z}^{\star})}{\widetilde{p}(\mathbf{z}^{(\tau)})q_k(\mathbf{z}^{\star}|\mathbf{z}^{(\tau)})}\right) Ak(z⋆,z(τ))=min(1,p (z(τ))qk(z⋆∣z(τ))p (z⋆)qk(z(τ)∣z⋆))
其中k标记出可能的转移集合中的成员,对于一个对称的提议分布, Metropolis-Hasting 准则会退化为 Metropolis 准则。
具体推导过程设计到马尔科夫链的知识,这里只记形式
11.2.7 吉布斯采样
吉布斯采样是一个简单的并且广泛应用的马尔科夫链蒙特卡洛算法,可以看做 Metropolis-Hasting 算法的一个具体的情形。
考虑我们项采样的概率分布 p ( z ) = p ( z 1 , … , z M ) p(z)=p(z_1,\ldots,z_M) p(z)=p(z1,…,zM),并且假设我们已经选择了马尔科夫链的某个初始状态。吉布斯采样的每个步骤涉及到将一个变量的值替换为以剩余变量的值为条件,从这个概率分布中抽取的那个变量的值。具体流程如下:
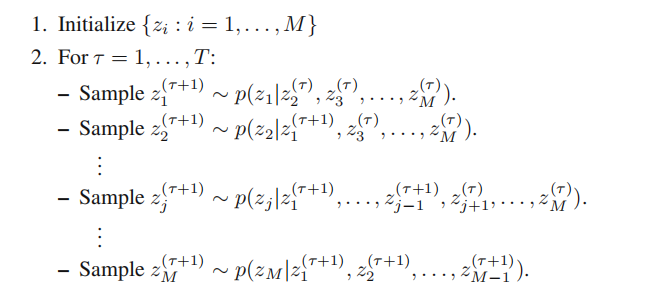
参考书:PRML
参考:PRML学习笔记(十一) - Pelhans 的博客
相关文章:
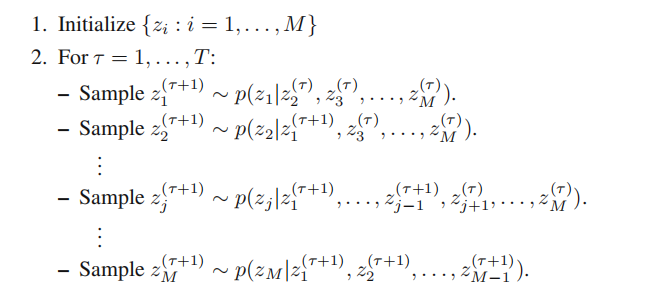
【机器学习】采样方法
文章目录 采样方法11.1 简介11.2 常见采样方法11.2.1 均匀分布采样11.2.2 逆变换采样11.2.3 拒绝采样11.2.4 重要采样11.2.5 Metropolis方法11.2.6 Metropolis-Hasting 算法11.2.7 吉布斯采样 采样方法 11.1 简介 什么是采样 从一个分布中生成一批服从该分布的样本,…...
Seata TCC 模式理论学习、生产级使用示例搭建及注意事项 | Spring Cloud55
一、前言 通过以下系列章节: docker-compose 实现Seata Server高可用部署 | Spring Cloud 51 Seata AT 模式理论学习、事务隔离及部分源码解析 | Spring Cloud 52 Spring Boot集成Seata利用AT模式分布式事务示例 | Spring Cloud 53 Seata XA 模式理论学习、使用…...

一文详解:Vue3中使用Vue Router
目录 安装和配置Vue Router安装Vue Router配置Vue Router Vue Router的基本概念Vue Router 的配置项介绍routes中的配置项介绍 路由跳转使用 router-link组件使用router.push函数 路由传参动态路由嵌套路由命名路由路由守卫全局路由守卫路由独享守卫 路由懒加载使用import()方式…...
C++开发—远程控制
C开发—远程控制 一,准备二,安装版本控制工具1,安装gitforwindows2,安装乌龟git1,安装乌龟git应用2,安装乌龟git对应的语言包 3,设置Visual Studio的git插件4,创建git项目 三&#x…...
)
【Python基础】Python数据容器(集合)
文章目录 数据容器:set(集合)集合的定义集合的常用操作-修改(1)添加新元素(2)移除元素(3)从集合中随机取出元素(4)清空集合(5)取出 两个集合的差集(6)消除 两个集合的差集(7)两个集合 合并(8)统计集合元素数量len()(9)集合的遍历 集合的特点 …...

高通 Camera HAL3:集成camxoverridesettings.txt到整机版本
camxoverridesettings.txt 是高通提供给开发者临时进行CAMX、CHI-CDK功能调试的一种方式,通过配置各种变量值然后写入到该文件,能控制Log打印、参数配置、数据dump等多种功能 这个文件需要集成在设备目录的vendor/etc/camera/里 因为camxoverridesetti…...

PHP面试题大全
一 、PHP基础部分 1、PHP语言的一大优势是跨平台,什么是跨平台? PHP的运行环境最优搭配为ApacheMySQLPHP,此运行环境可以在不同操作系统(例如windows、Linux等)上配置,不受操作系统的限制,所以…...

Linux发送接收邮件
目录 一、实验 1.linux用户发送给linux中的其它用户 2.linux用户发送给外网用户 一、实验 1.linux用户发送给linux中的其它用户 (1)使用命令 yum install -y sendmail 安装sendmail软件 (2)使用yum install -y mailx 安装 mail…...

SpringBoot-【回顾】
第一个SpringBoot程序 自动装配原理 Springboot的自动装配实际上就是为了从Spring.factories文件中获取到对应的需要进行自动装配的类,并生成相应的Bean对象,然后将它们交给Spring容器来帮我们进行管理 启动器:以starter为标记 EnableAuto…...
)
Python模拟试卷2023(1)
模拟试卷(1) 一、简答题 (共8题,100分) 1、已知有列表lst[54,36,75,28,50],请完成一下操作: 1、在列表尾部插入元素42 2、在元素28前面插入66 3、删除并输出28 4、将列表按降序排序 5、清空整个列表 lst[54,3…...

常量接口 vs 常量类 vs 枚举区别
把常量定义在接口里与类里都能通过编译,那2者到底有什么区别呢? 那个更合理? 常量接口 public interface ConstInterfaceA {public static final String CONST_A "aa";public static final String CONST_C "cc"; } 存在…...

第二章 模态命题:必然、可能
第二章 模态命题:必然、可能 第一节 模态命题-句式转换-逻辑转换 题-模态命题-句式转换-逻辑转换:①不一定不可能;②不一定可能不未必。 1.唐代韩愈在《师说》中指出:“孔子曰:三人行,则必有我师。是故…...

Selenium 必了解—如何测试REST API
目录 前言: Web UI测试存在的问题: REST API测试: 依赖包 程序示例: 1-获取联系人 2-GET Request: 3-POST Request: 4- 编辑请求 5- 删除请求 前言: Selenium WebDriver 可以用于测试 Web 应用的…...

pytorch安装老版本
比如1.7.1, cuda 10.1 pip install torch1.7.1cu101 -f https://download.pytorch.org/whl/torch_stable.html官网查看有哪些可以装的: https://download.pytorch.org/whl/torch_stable.html...

怎么自学电脑编程
首要之首:不要急于选择一种语言 新手们有一个常见的错误就是犹豫于判断哪种编程语言是做好的、最该先学的。 我们有很多的选择,但你不能说那种语言最好。 我们应该理解:说到底,什么语言并不重要。 重要的是理解数据结构、控制逻辑…...
)
【华为OD统一考试B卷 | 100分】斗地主之顺子(C++ Java JavaScript Python)
文章目录 题目描述输入描述输出描述用例C++JavajavaScriptpython题目描述 在斗地主扑克牌游戏中, 扑克牌由小到大的顺序为:3,4,5,6,7,8,9,10,J,Q,K,A,2,玩家可以出的扑克牌阵型有:单张、对子、顺子、飞机、炸弹等。 其中顺子的出牌规则为:由至少5张由小到大连续递增的扑…...
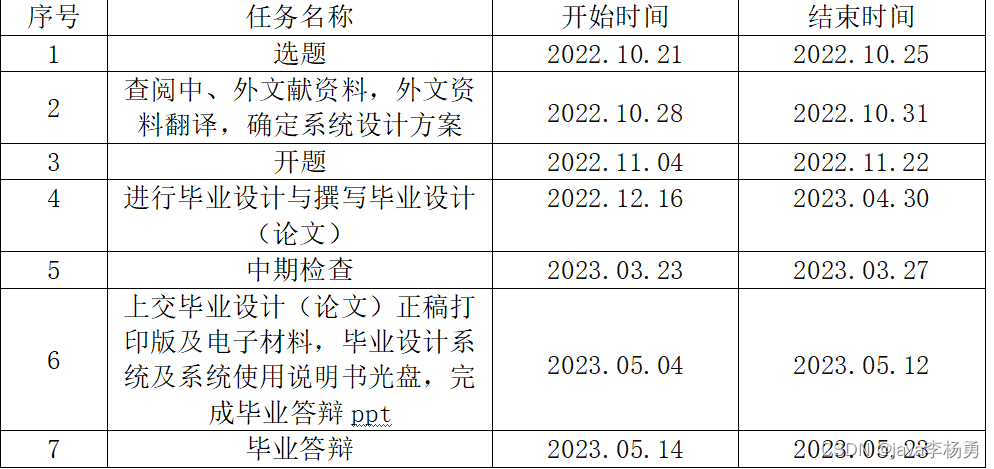
案例39:基于Java办公自动化管理系统开题报告设计
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

基于山景BP10128音频处理器高通滤波器算法设计
+ hezkz17进数字音频答疑 山景BP10128音频处理器是一款高性能的数字信号处理器,专门用于音频信号的处理和增强。它采用先进的数字信号处理技术和算法,能够对音频信号进行实时处理,并且具有高效、稳定、可靠等特点。 该处理器具有以下主要功能: 均衡器:支持低音、中音、…...

docker搭建本地私有仓库
一、搭建本地私有仓库 有时候使用Docker Hub这样的公共仓库可能不方便,这种情况下用户可以使用registry创建一个本地仓库供私人使用,这点跟Maven的管理类似。 使用私有仓库有许多优点: 1)节省网络带宽,针对于每个镜像…...
)
Asp.net某店POS积分管理系统-清除履历表、日志表、月购买额(源代码+论文)
大型百货店作为日常生活中不可缺少的一部分,给人们的生活提供了很大的方便。而为这样一个庞大而复杂的购物平台,提供一套完备的管理系统支持是很必要的。在现代销售行业中,会员制、积分管理、代金消费的概念已经越来越普及。为了吸引更多消费者,加大销售企业的竞争力。就需…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
