八大排序算法之归并排序(递归实现+非递归实现)
目录
一.归并排序的基本思想
归并排序算法思想(排升序为例)
二.两个有序子序列(同一个数组中)的归并(排升序)
两个有序序列归并操作代码:
三.归并排序的递归实现
递归归并排序的实现:(后序遍历递归)
递归函数抽象分析:
四.非递归归并排序的实现
1.非递归归并排序算法思想:
2.算法实现
初步非递归归并排序函数:
一般情况下(所排序数组元素个数不为编辑)边界条件分析:
经过边界修正后的非递归归并排序函数
排序实测:
一.归并排序的基本思想
- 归并排序是基于分治思想和归并操作而设计出来的一种高效排序算法
- 所谓的归并操作就是将两个有序的子序列合并为一个有序序列的操作(归并操作算法的时间复杂度为O(N+M),N+M分别为两个子数组的元素个数)
归并排序算法思想(排升序为例)
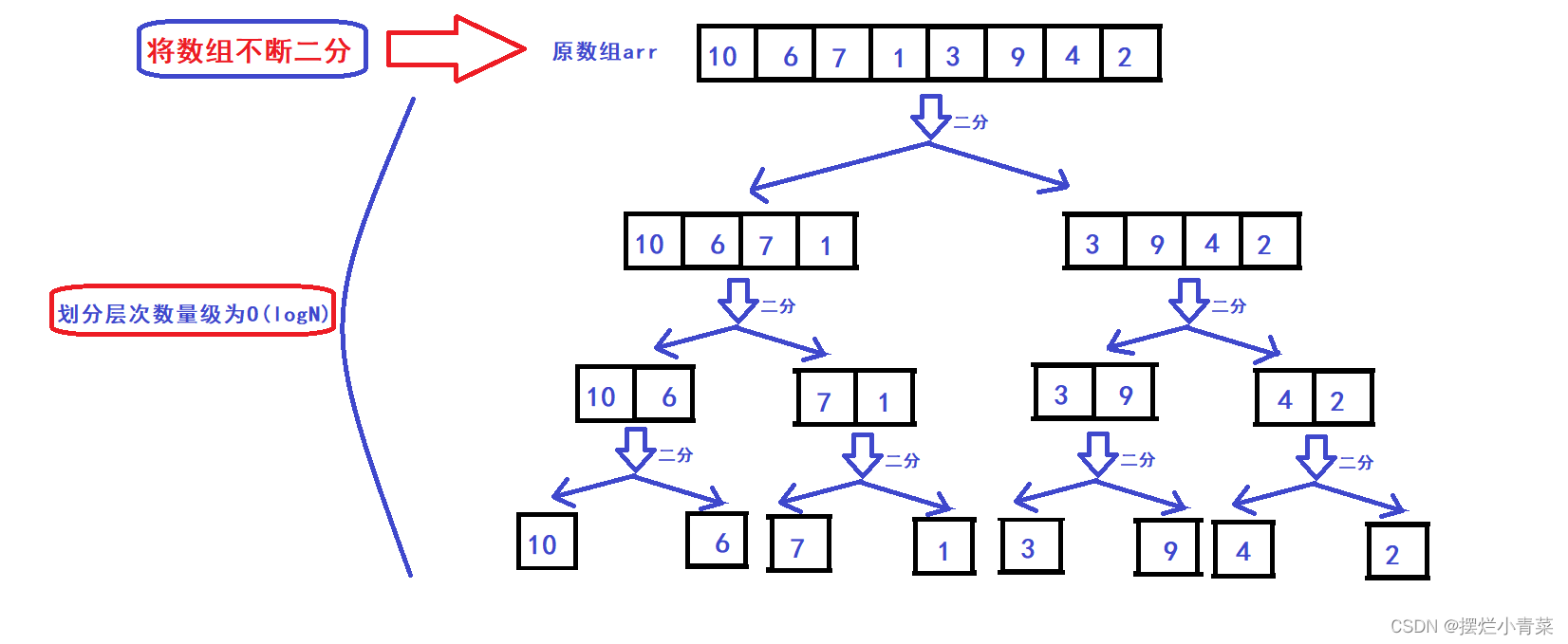
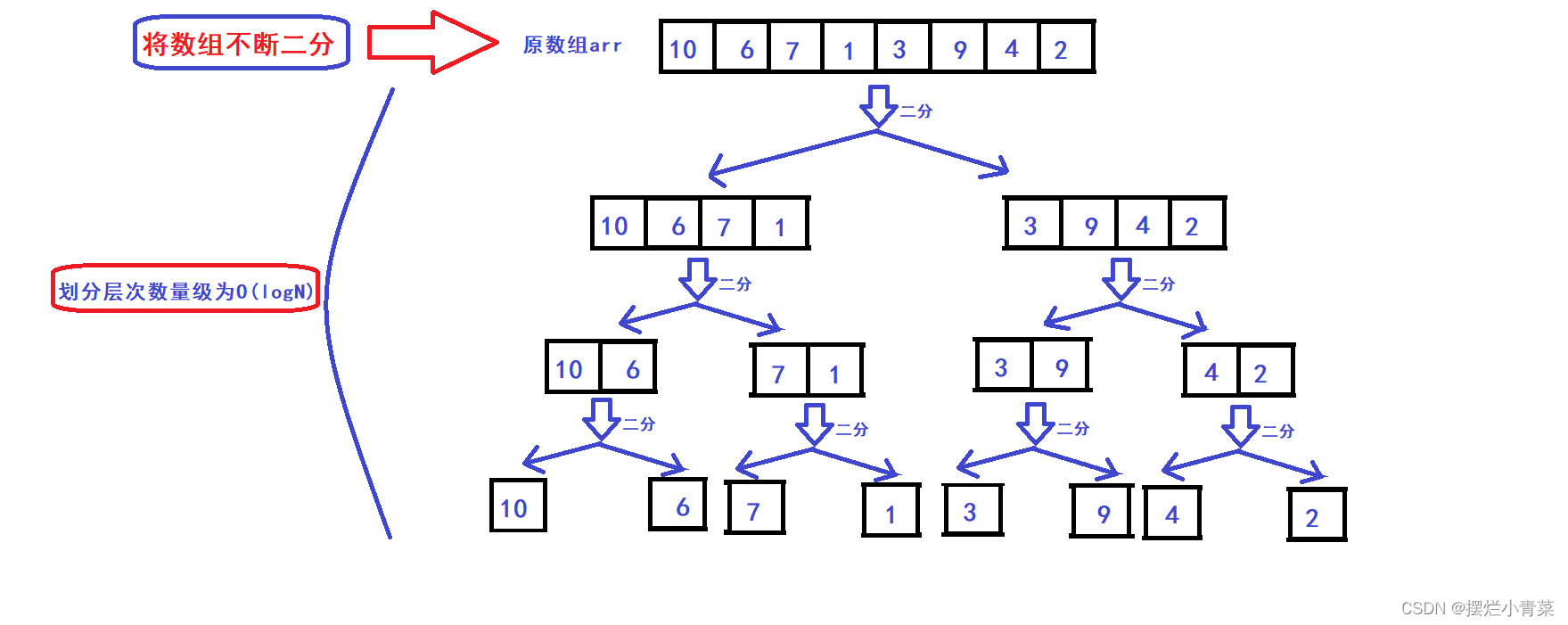
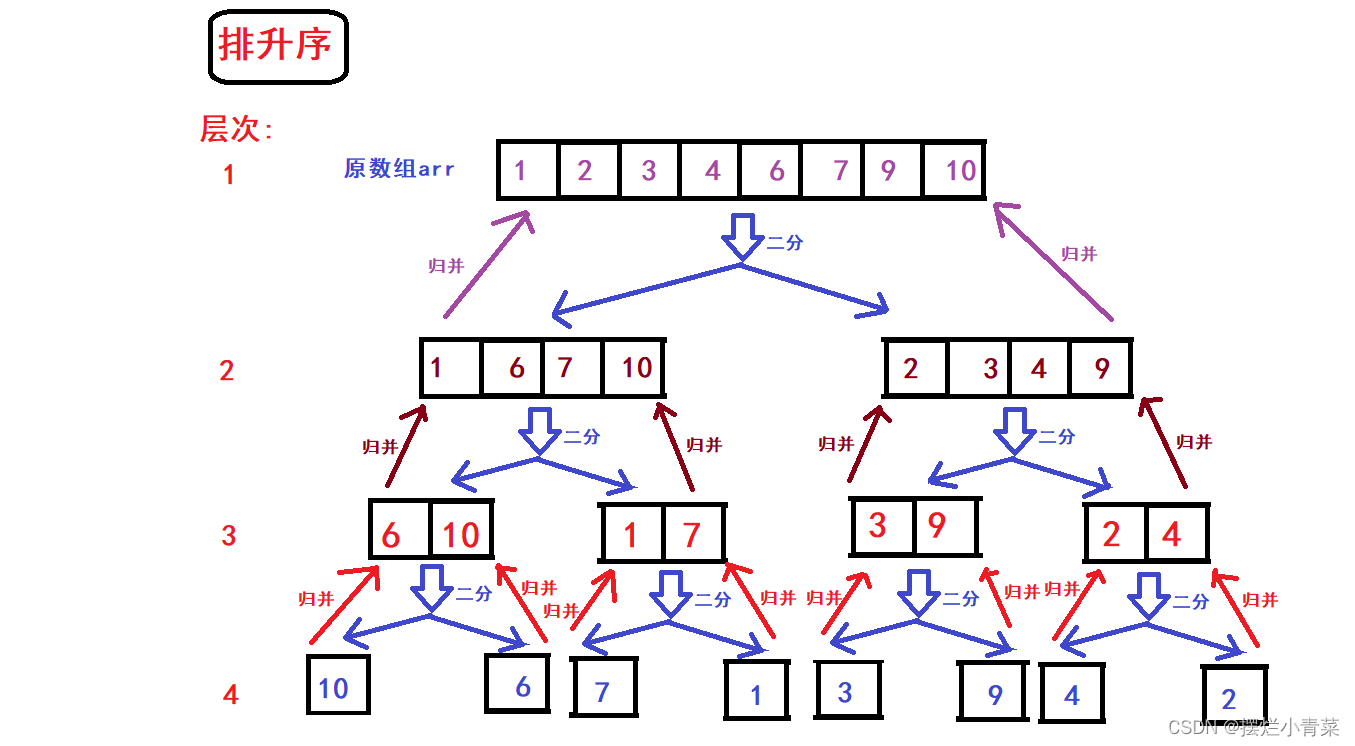
- 假设数组有N个元素,先将数组不断地二分,直到将数组划分为N个由单个元素构成的子数组,整个划分过程中所有子数组构成满二叉树(或接近满二叉树)的逻辑结构,如图:
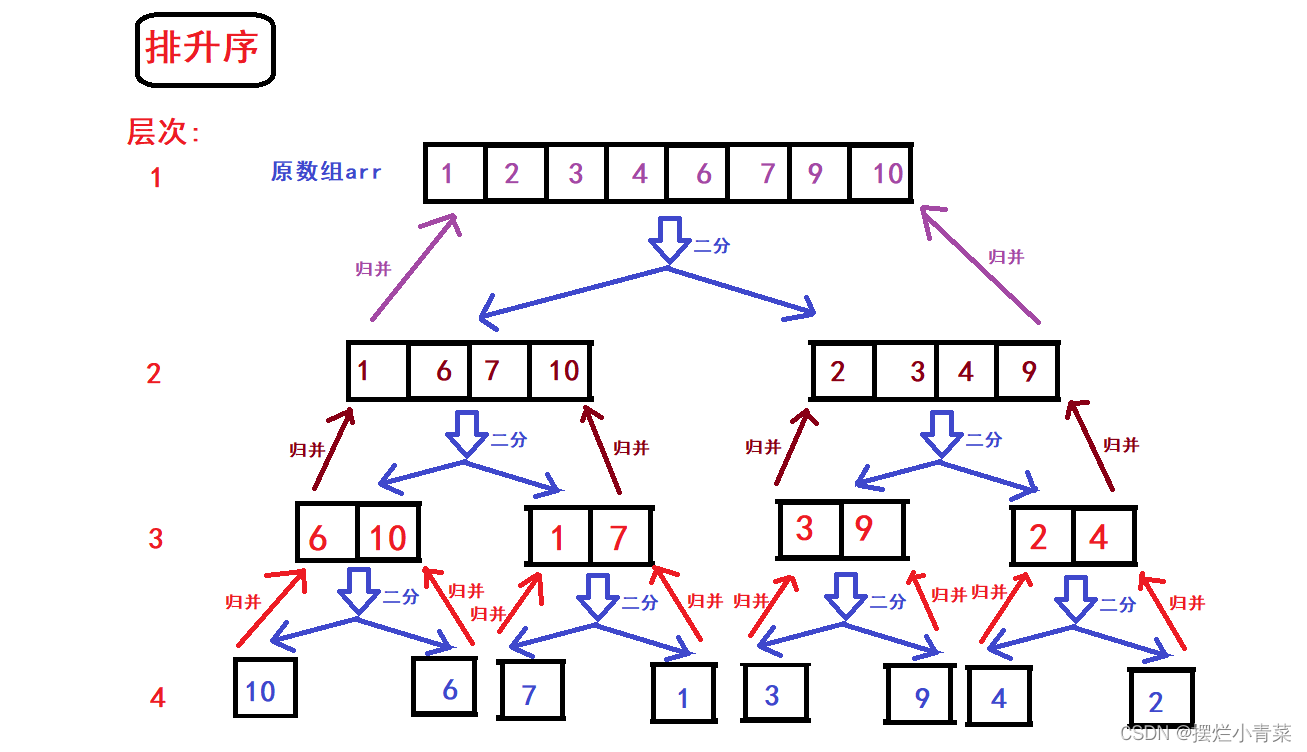
- 数组划分完后再逐层向上将二叉树兄弟结点子数组(具有相同前驱结构)两两进行归并操作完成排序:
- 归并操作算法的时间复杂度为O(M1+M2),M1+M2分别为两个子数组的元素个数,因此二叉树一层子数组的两两归并操作的总时间复杂度为O(N)(N表示原数组的元素个数),而满二叉树的层次数量级为O(logN),因此归并排序的总体时间复杂度为O(NlogN)
- 由于归并排序的数组划分每次都是严格地二分,因此每次排序(无论具体面对怎样的序列)子数组划分结构都是稳定的满二叉树(或接近满二叉树)结构,因此归并排序的时间复杂度在各种情况下都不会有变化(不会像快排,希尔排那样由于所处理的序列的逆序数的差异而导致算法时间复杂度有所变化)
- 然而由于有序序列归并操作需要额外开辟数组来完成,因此归并排序有较大的空间消耗,这是归并排序的一个缺陷
二.两个有序子序列(同一个数组中)的归并(排升序)
函数首部:
void MergeSort(int* arr,int* tem, int left,int right)arr是被分割的原数组,tem是用于归并操作的临时数组,left是arr的左端下标,right是arr的右端下标
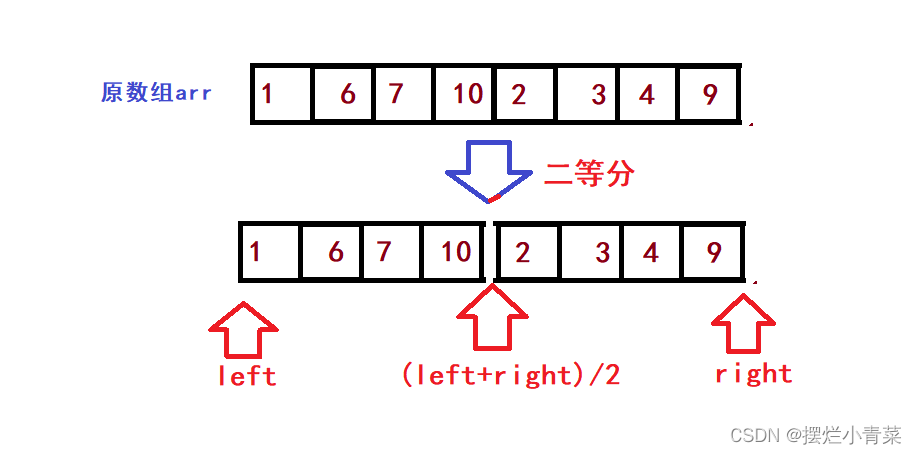
- 假设数组arr被二等分为两个子序列(两个子序列都是有序的):
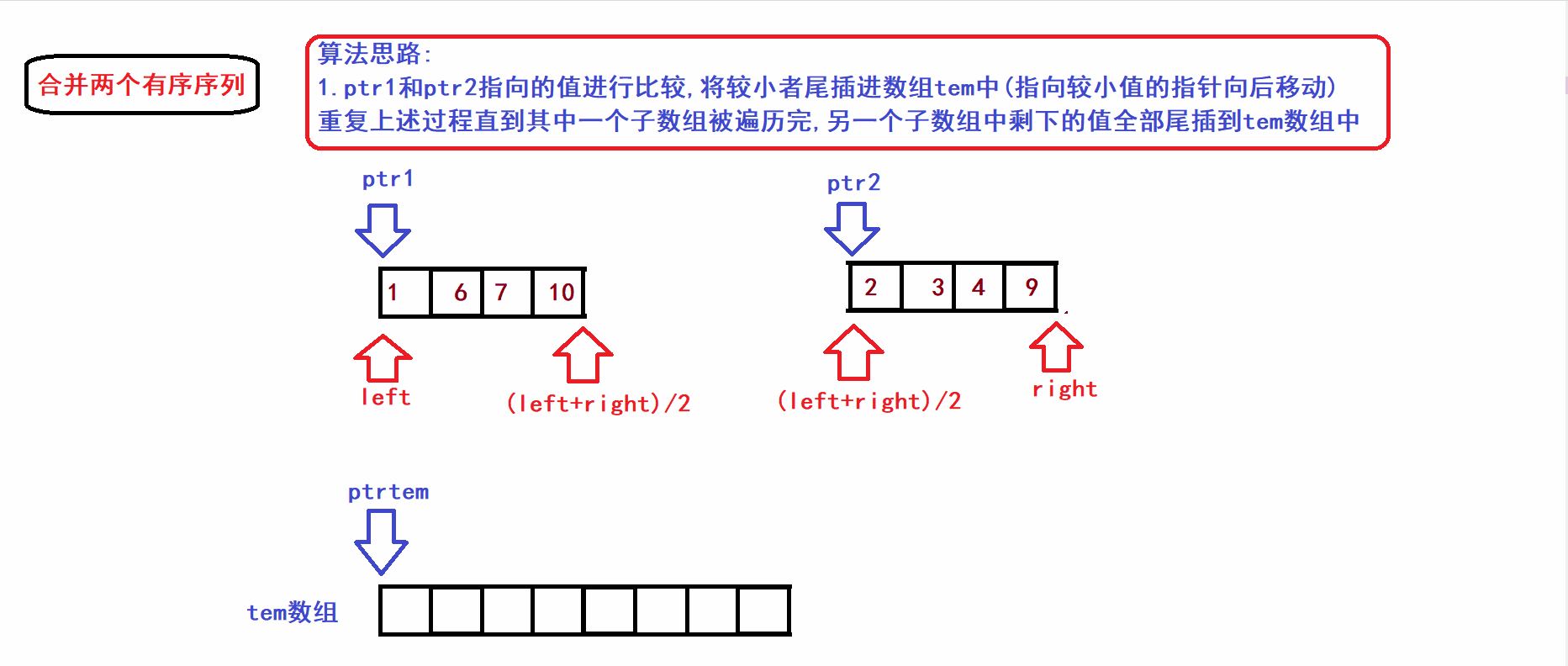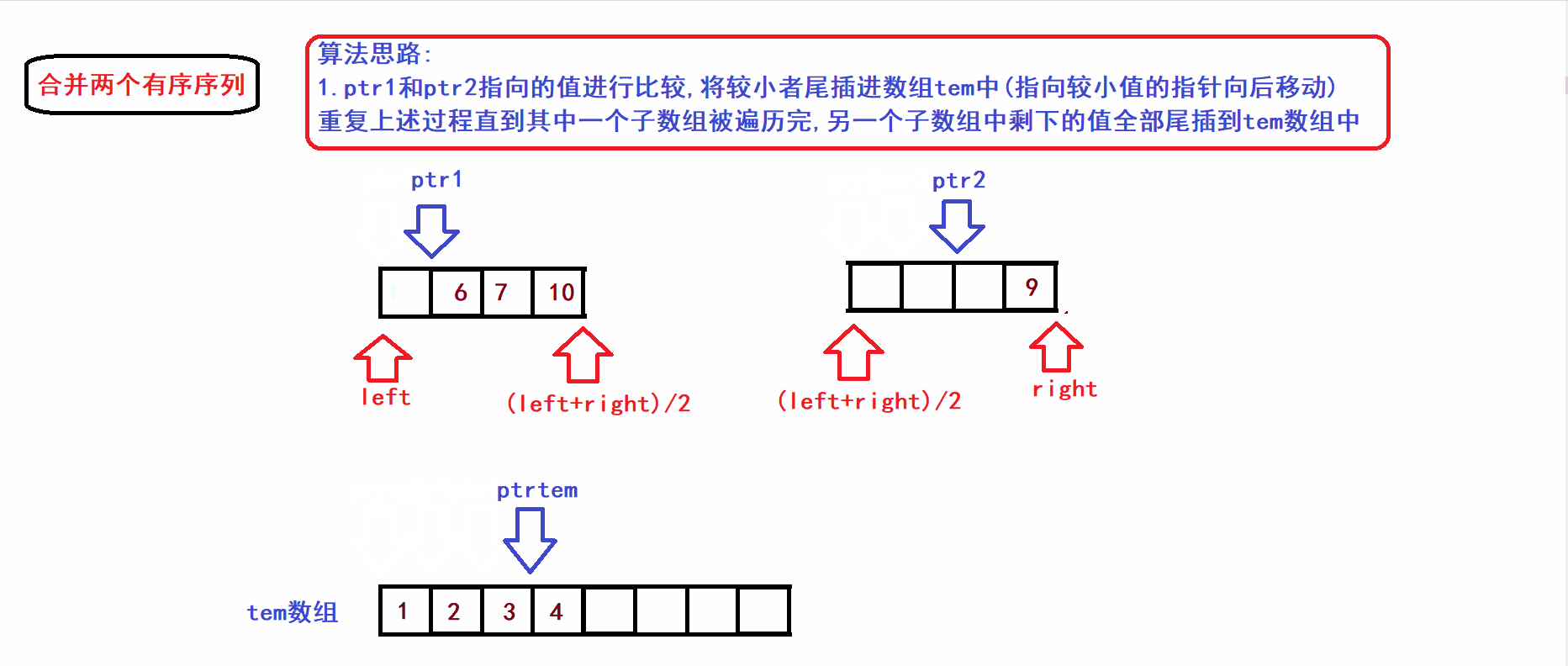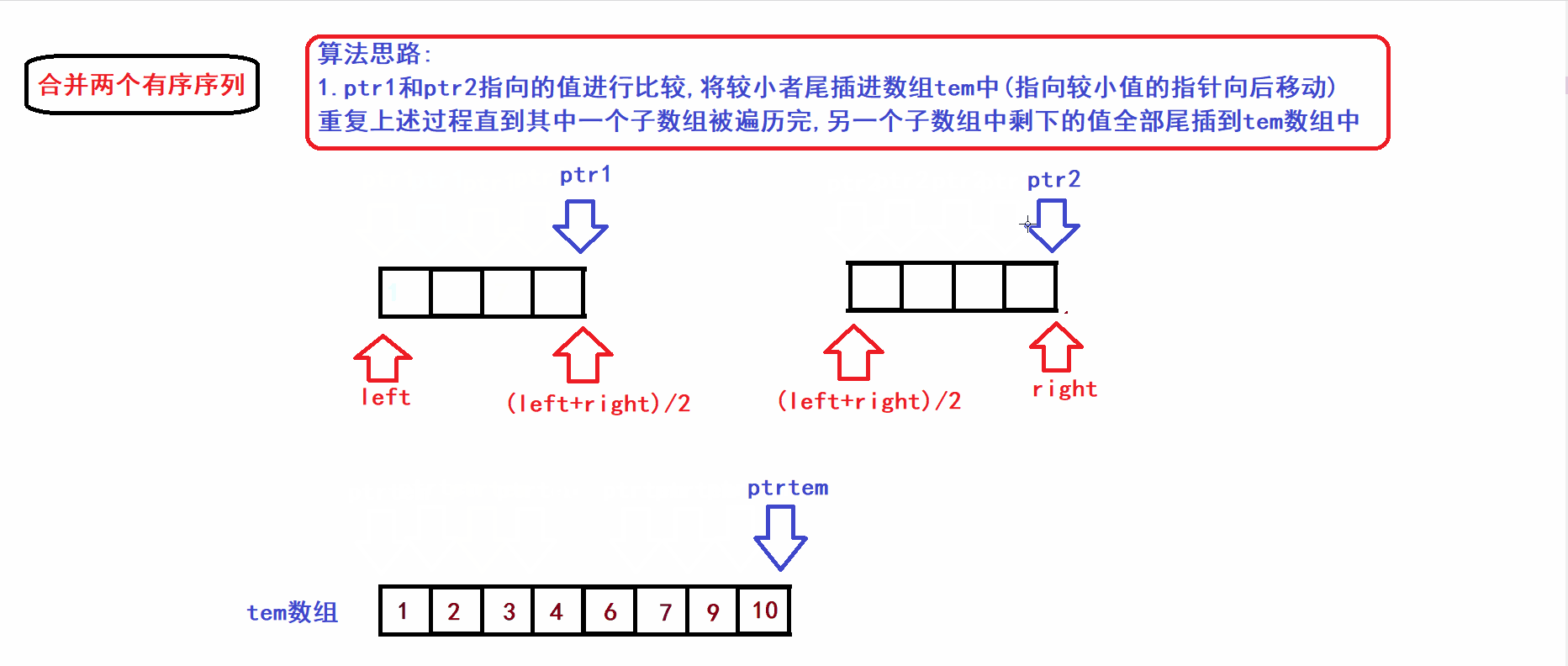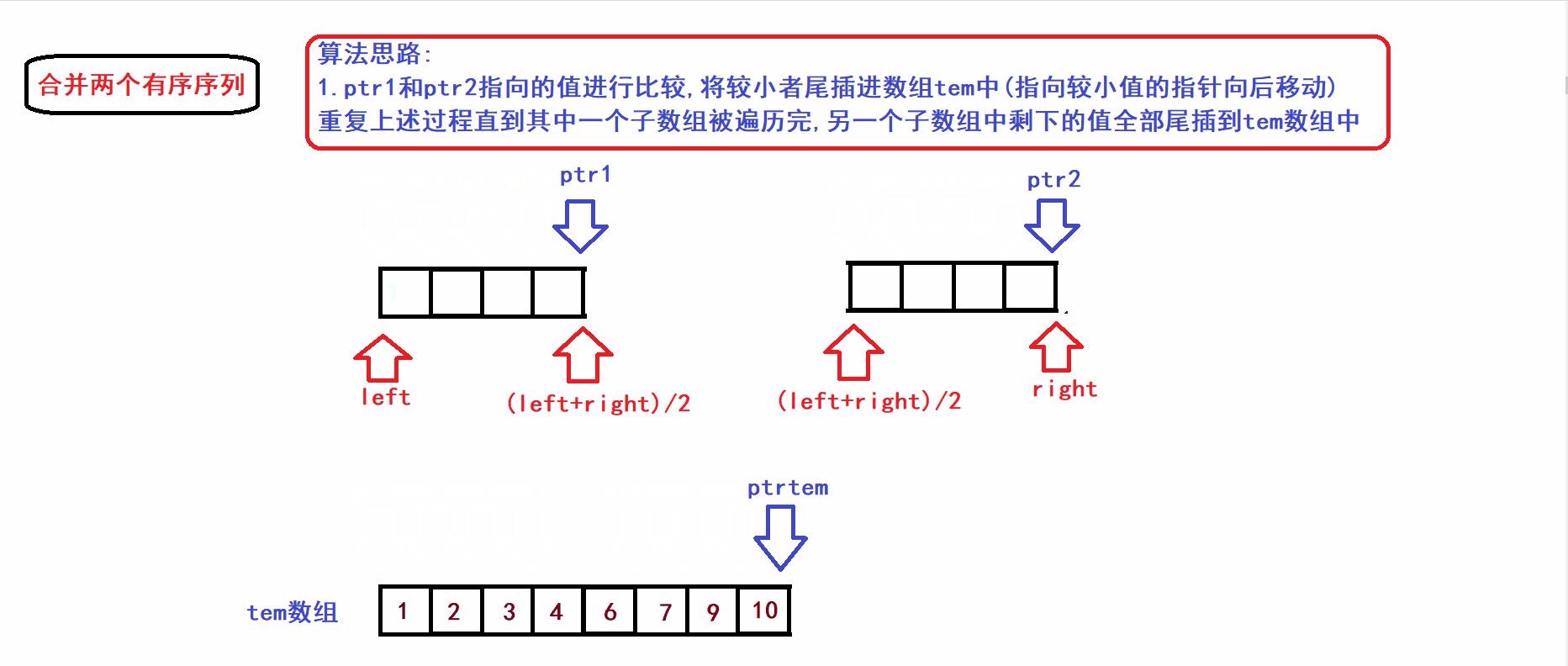
- 接下来我们将上图中的[left,(left+right)/2)和[(left+right)/2),right)两个子序列(有序)合并到一个tem数组中构成一个新的有序序列(利用三指针操作完成归并):
- 从算法gif中不难看出,归并操作的时间复杂度与两个子数组的元素个数成线性关系
两个有序序列归并操作代码:
void MergeSort(int* arr,int* tem, int left,int right) {int mid = left + (right - left) / 2; //找到数组[left,right]的中间分割点int ptr1 = left; //ptr1指向左子数组的首元素int ptr2 = mid; //ptr2指向右子数组的首元素int ptrtem = left; //ptrtem用于在tem数组中尾插数据while (ptr1 < mid && ptr2 < right) //ptr1和ptr2其中一个遍历完子数组就停止循环{//将较小元素尾插进tem数组中if (arr[ptr1] > arr[ptr2]){tem[ptrtem] = arr[ptr2];++ptrtem;++ptr2;}else{tem[ptrtem] = arr[ptr1];++ptrtem;++ptr1;}}//将未被遍历完的子数组剩下的元素尾插到tem数组中while (ptr1 < mid){tem[ptrtem] = arr[ptr1];++ptrtem;++ptr1;}while (ptr2 < right){tem[ptrtem] = arr[ptr2];++ptrtem;++ptr2;}//将归并好的有序序列拷贝到原数组arr上for (int i = left; i < right; ++i){arr[i] = tem[i];} }
三.归并排序的递归实现
递归函数首部:
void MergeSort(int* arr,int* tem, int left,int right)arr是被分割的原数组,tem是用于归并操作的临时数组,left是arr的子数组的左端下标,right是arr的子数组的右端下标
- 在进行子数组两两归并之前,我们先要进行数组的二分分治:
- 我们可以通过分治递归来完成数组的整个二分过程(每个子数组的区间端点下标都被存储在递归函数的各函数栈帧中):(数组二分的递归框架)
void MergeSort(int* arr, int* tem, int left, int right) {if (right <= left+1) //当子数组只剩一个元素时停止划分{return;}int mid = left + (right - left) / 2;MergeSort(arr, tem, left, mid); //划分出的左子数组MergeSort(arr, tem, mid, right); //划分出的右子数组//左右子数组都有序后完成左右子数组的归并 }
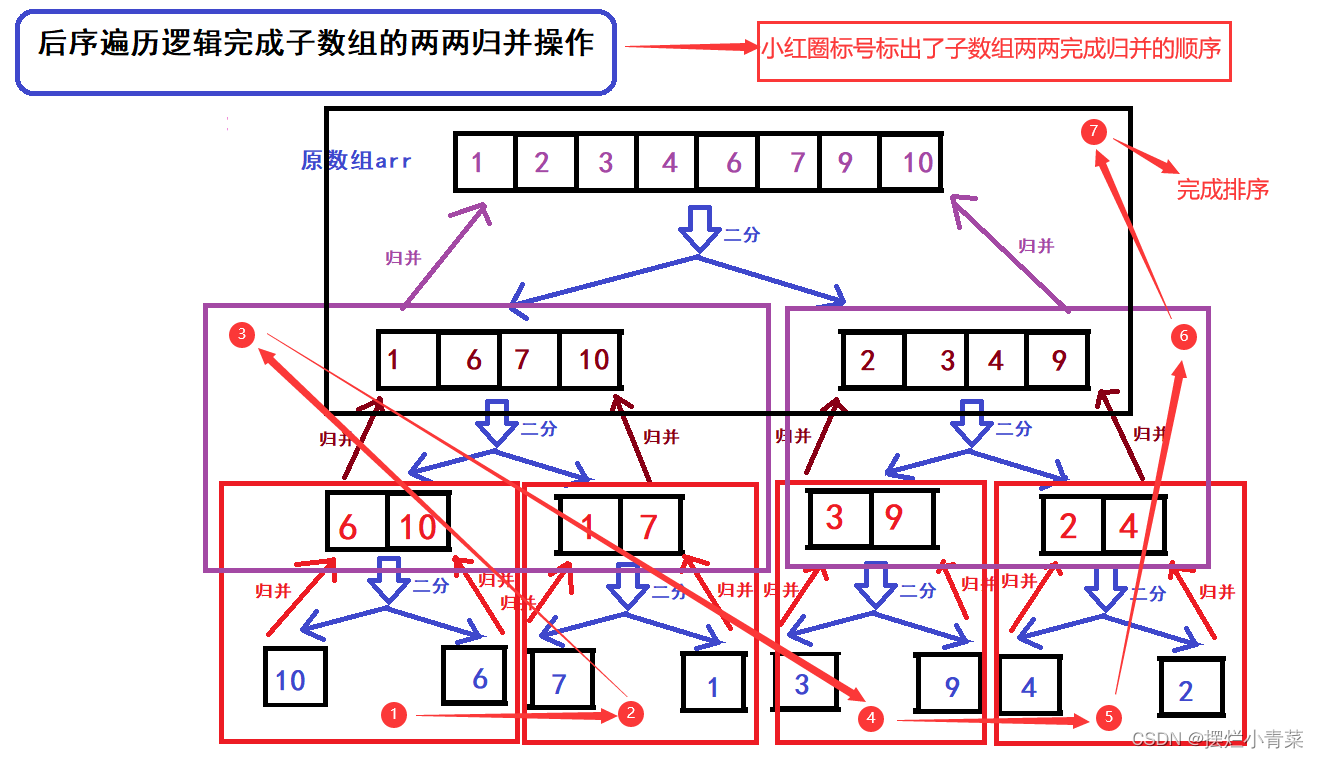
观察递归图解,有序序列两两归并的过程只能发生在上图中的第7,第13,第14,第21,第27,第28,第29步骤中,因此整个排序过程满足分治递归的后序遍历逻辑
递归归并排序的实现:(后序遍历递归)
- 左右子数组(有序)归并的代码段位于函数中两个递归语句之后
void MergeSort(int* arr, int* tem, int left, int right) {if (right <= left+1) //当子数组只剩一个元素时停止划分{return;}int mid = left + (right - left) / 2;MergeSort(arr, tem, left, mid); //划分出的左子数组MergeSort(arr, tem, mid, right); //划分出的右子数组//后序遍历,归并过程发生在两个递归语句之后//左右子数组都有序后完成左右子数组的归并int ptr1 = left; //ptr1指向左子数组的首元素int ptr2 = mid; //ptr2指向右子数组的首元素int ptrtem = left; //ptrtem用于在tem数组中尾插数据while (ptr1 < mid && ptr2 < right) //ptr1和ptr2其中一个遍历完子数组就停止循环{//将较小元素尾插进tem数组中if (arr[ptr1] > arr[ptr2]){tem[ptrtem] = arr[ptr2];++ptrtem;++ptr2;}else{tem[ptrtem] = arr[ptr1];++ptrtem;++ptr1;}}//将未被遍历完的子数组剩下的元素尾插到tem数组中while (ptr1 < mid){tem[ptrtem] = arr[ptr1];++ptrtem;++ptr1;}while (ptr2 < right){tem[ptrtem] = arr[ptr2];++ptrtem;++ptr2;}//将归并好的有序序列拷贝到原数组arr(相应下标位置)for (int i = left; i < right; ++i){arr[i] = tem[i];} }
- 注意细节:

递归函数抽象分析:
- 递归函数MergeSort(arr,tem,left,right)可以抽象为:借助tem数组完成arr数组[left,right)区间序列的排序过程
- 于是可以抽象出递推公式:MergeSort(arr,tem,left,right) = MergeSort(arr,tem,left,left + (right - left) / 2) + MergeSort(arr,tem,left + (right - left) / 2,right) +{子数组[left,left + (right - left) / 2))和子数组[left + (right - left) / 2,right)的有序合并}
- 递归公式的含义是:完成arr数组[left,right)区间序列排序的过程可以拆分为如下三个步骤:
- 先完成左子区间[left,left + (right - left) / 2)的排序
- 再完成右子区间[left + (right - left) / 2,right)的排序
- 最后将左右子区间进行归并完成[left,right)区间序列的排序
- 将MergeSort函数进行一下简单的封装供外界调用:
void _MergeSort(int* arr, int size) {assert(arr);int* tem = (int*)malloc(sizeof(int) * size);assert(tem);MergeSort(arr, tem, 0, size);free(tem); }- arr是待排序数组,size是数组的元素个数,MergeSort是归并排序递归函数
四.非递归归并排序的实现
1.非递归归并排序算法思想:
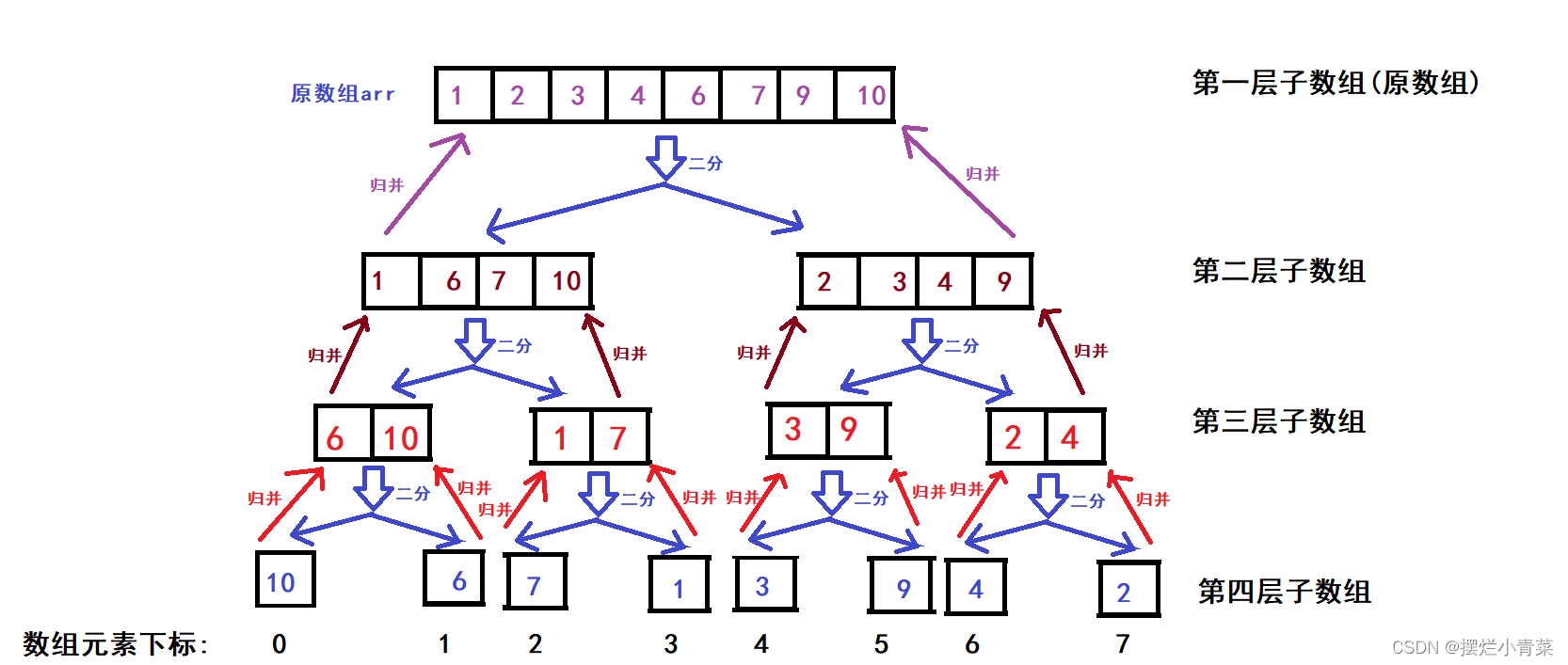
- 归并排序过程中数组逐步被二分的图示:
- 归并排序的递归实现通过后序遍历逻辑来完成各个子数组的两两归并的操作:
- 然而我们也可以利用类似于层序遍历的逻辑来实现子数组两两归并的过程:
从最高层子数组开始进行兄弟子数组的两两归并,完成了一层子数组的归并再继续完成前一层子数组的归并直到最后完成原数组的排序,我们可以通过循环来实现这个过程
2.算法实现
- 非递归归并排序函数首部:
void MergeSortNonR(int* arr, int size)arr代表待排序的数组,size为待排序数组的元素个数
- 先假设所处理的数组的元素个数:N=
(即数组刚好能被完全二分n次)
- 取gap作为二叉树结构某层次各子数组的元素个数:gap初值为1(最深层子数组元素个数为1),随后gap以gap=2*gap的方式递增,用gap来控制排序函数最外层循环:
for (int gap = 1; gap < size; gap *= 2) //完成logN个层次的子数组的归并{}该循环能进行log(size)次,对于每个gap值完成一个层次的子数组的两两归并:
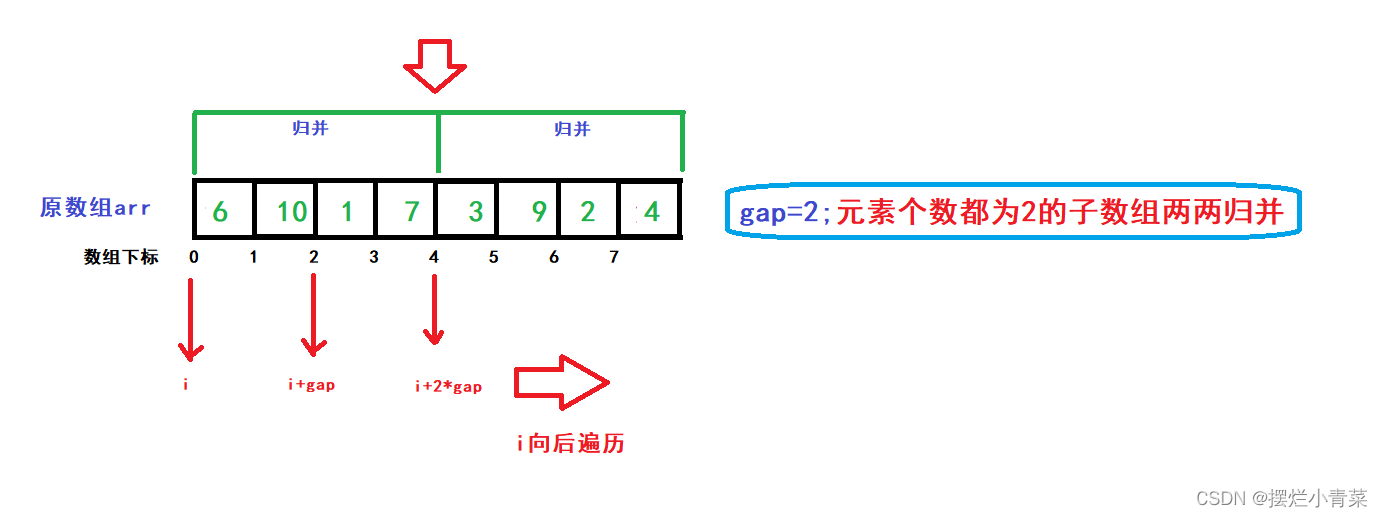
再使用一个变量i来遍历每一个gap情形下的各个进行归并的序列组(每个序列组由两个子数组构成):
for (int gap = 1; gap < size; gap *= 2) //完成logN个层次的子数组的归并{for (int i = 0; i < size; i += 2 * gap) //i每次跳过一个归并序列组(每个序列组有两个子数组){//对子数组[i,i+gap)和子数组[i+gap,i+2*gap)进行归并操作}}图解:
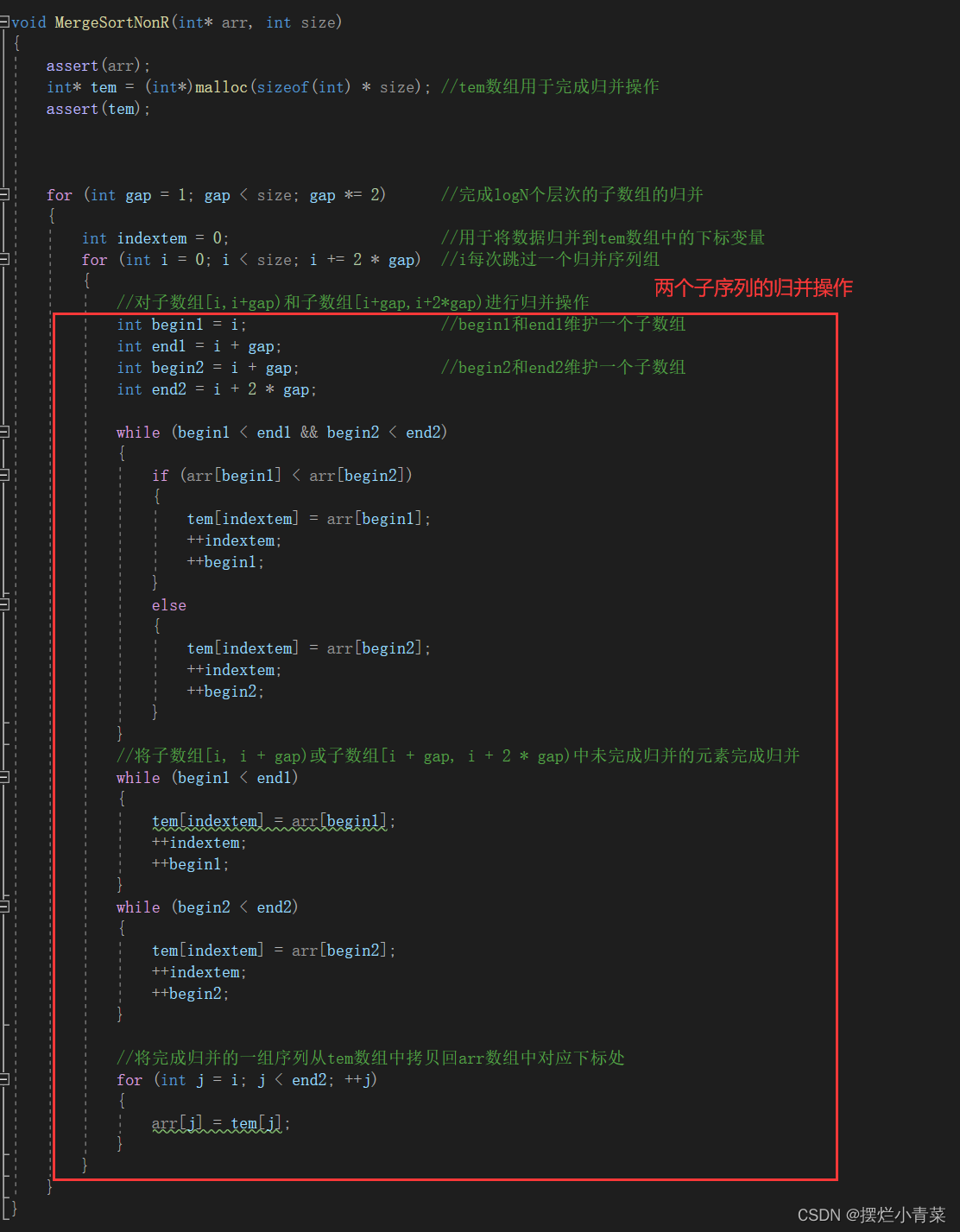
初步非递归归并排序函数:
void MergeSortNonR(int* arr, int size) {assert(arr);int* tem = (int*)malloc(sizeof(int) * size); //tem数组用于完成归并操作assert(tem);for (int gap = 1; gap < size; gap *= 2) //完成logN个层次的子数组的归并{int indextem = 0; //用于将数据归并到tem数组中的下标变量for (int i = 0; i < size; i += 2 * gap) //i每次跳过一个归并序列组(每个序列组有两个子数组){//对子数组[i,i+gap)和子数组[i+gap,i+2*gap)进行归并操作int begin1 = i; //begin1和end1维护一个子数组int end1 = i + gap; int begin2 = i + gap; //begin2和end2维护一个子数组int end2 = i + 2 * gap;while (begin1 < end1 && begin2 < end2){if (arr[begin1] < arr[begin2]){tem[indextem] = arr[begin1];++indextem;++begin1;}else{tem[indextem] = arr[begin2];++indextem;++begin2;}}//将子数组[i, i + gap)或子数组[i + gap, i + 2 * gap)中未完成归并的元素完成归并while (begin1 < end1){tem[indextem] = arr[begin1];++indextem;++begin1;}while (begin2 < end2){tem[indextem] = arr[begin2];++indextem;++begin2;}//将完成归并的一组序列从tem数组中拷贝回arr数组中对应下标处for (int j = i; j < end2; ++j){arr[j] = tem[j];}}}free(tem); }
两个子数组的归并操作见前面的章节;
初步非递归归并排序函数只能处理元素个数为
(即数组刚好能被完全二分n次)的数组
想要使排序函数能够处理任意元素个数的数组,我们就必须进行算法边界条件分析和边界修正
一般情况下(所排序数组元素个数不为
)边界条件分析:
- 设待排序数组的元素个数为size
- 函数中只有下标end1,begin2,end2存在越界的可能(函数中begin1和end1,begin2和end2分别用于维护两个在数组arr中待归并的相邻子数组)
当所处理的数组元素个数不为
时,可能会出现下图中两种下标越界情况
- end1(end1==begin2)越界(end1>size)(此时end2一定也越界)
此时可以直接break终止i控制的循环(end1>size说明arr数组按照gap划分后尾部待归并区间数量只有一个,无须进行归并操作)
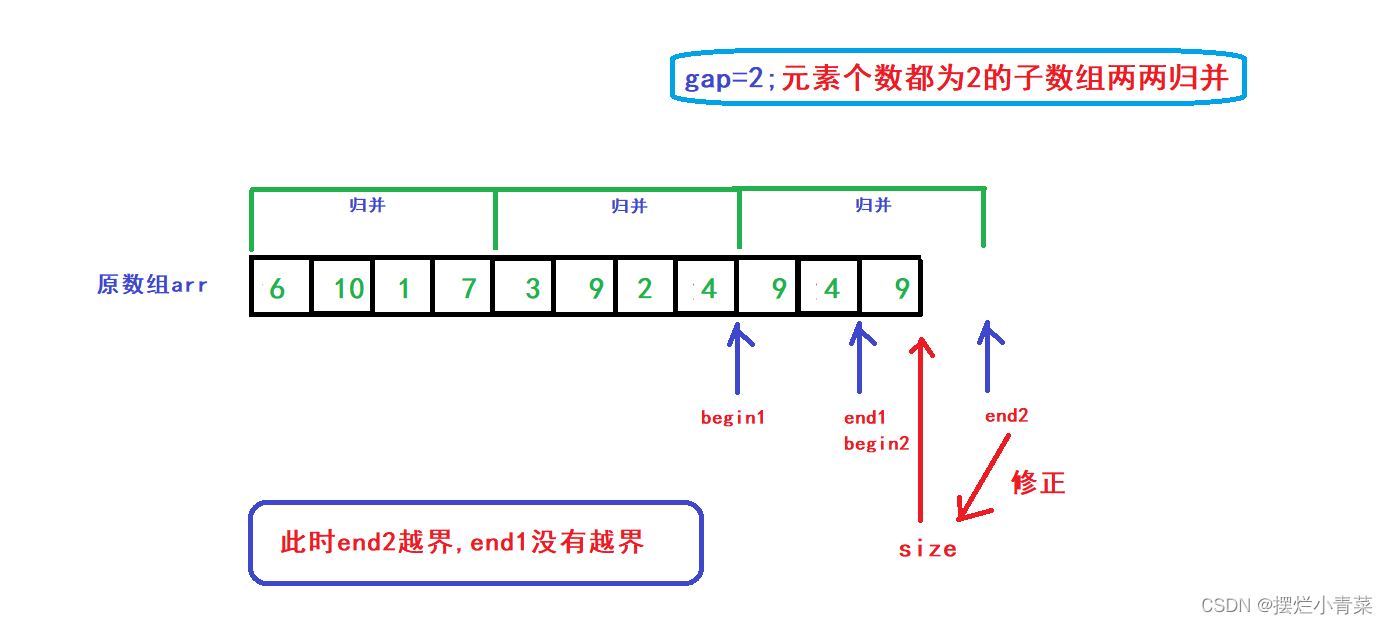
end2越界(end2>size)(end1没越界即(end1<size))
此时要将end2修正为size,后续便可以完成arr数组(按照gap划分后)尾部剩余的两个子数组的归并操作:
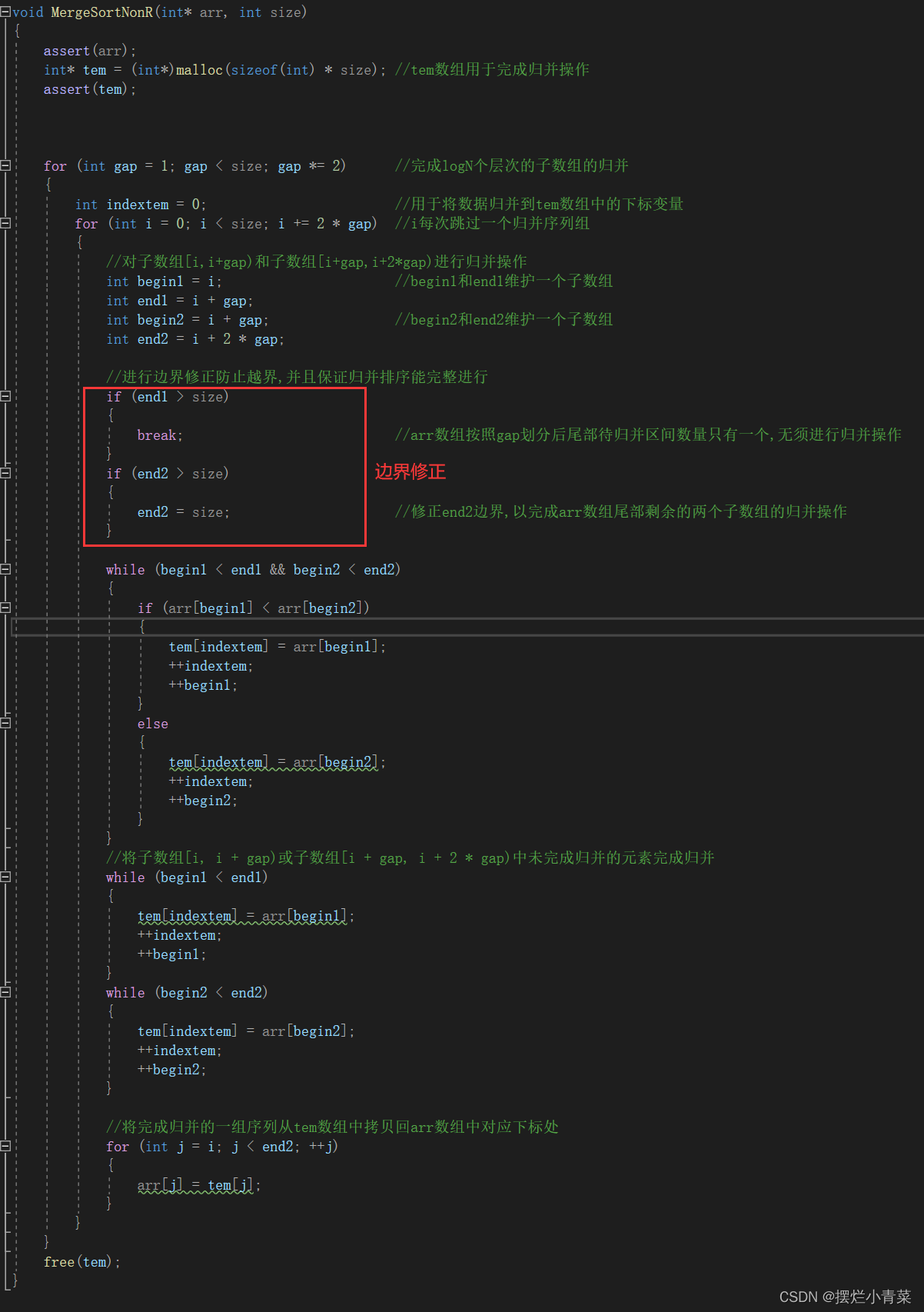
经过边界修正后的非递归归并排序函数
void MergeSortNonR(int* arr, int size) {assert(arr);int* tem = (int*)malloc(sizeof(int) * size); //tem数组用于完成归并操作assert(tem);for (int gap = 1; gap < size; gap *= 2) //完成logN个层次的子数组的归并{int indextem = 0; //用于将数据归并到tem数组中的下标变量for (int i = 0; i < size; i += 2 * gap) //i每次跳过一个归并序列组{//对子数组[i,i+gap)和子数组[i+gap,i+2*gap)进行归并操作int begin1 = i; //begin1和end1维护一个子数组int end1 = i + gap; int begin2 = i + gap; //begin2和end2维护一个子数组int end2 = i + 2 * gap;//进行边界修正防止越界,并且保证归并排序能完整进行if (end1 > size){break; //arr数组按照gap划分后尾部待归并区间数量只有一个,无须进行归并操作}if (end2 > size){end2 = size; //修正end2边界,以完成arr数组尾部剩余的两个子数组的归并操作}while (begin1 < end1 && begin2 < end2){if (arr[begin1] < arr[begin2]){tem[indextem] = arr[begin1];++indextem;++begin1;}else{tem[indextem] = arr[begin2];++indextem;++begin2;}}//将子数组[i, i + gap)或子数组[i + gap, i + 2 * gap)中未完成归并的元素完成归并while (begin1 < end1){tem[indextem] = arr[begin1];++indextem;++begin1;}while (begin2 < end2){tem[indextem] = arr[begin2];++indextem;++begin2;}//将完成归并的一组序列从tem数组中拷贝回arr数组中对应下标处for (int j = i; j < end2; ++j){arr[j] = tem[j];}}}free(tem); }
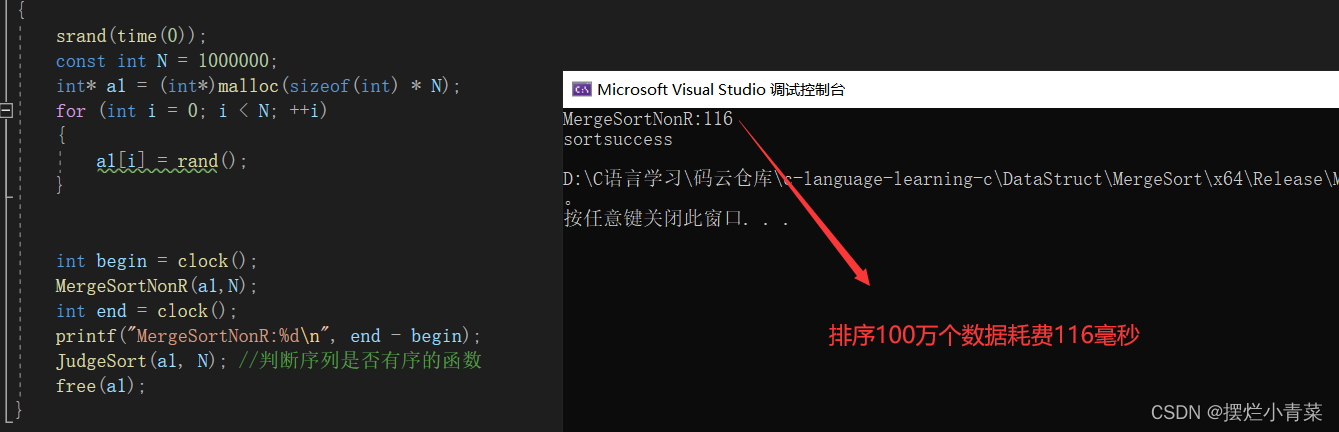
排序实测:
int main() {//排序100万个数据srand(time(0));const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();}int begin = clock();MergeSortNonR(a1,N);int end = clock();printf("MergeSortNonR:%d\n", end - begin);JudgeSort(a1, N); //判断序列是否有序的函数free(a1); }
- 非递归归并排序和递归归并排序在算法思想上没有任何区别(只是子数组归并的顺序不同而已) 两者的时间复杂度都是O(NlogN),空间复杂度都是O(N)(算法中需要开辟额外的数组tem来完成子序列两两归并操作),但是递归归并排序有额外的系统栈开销.

相关文章:

八大排序算法之归并排序(递归实现+非递归实现)
目录 一.归并排序的基本思想 归并排序算法思想(排升序为例) 二.两个有序子序列(同一个数组中)的归并(排升序) 两个有序序列归并操作代码: 三.归并排序的递归实现 递归归并排序的实现:(后序遍历递归) 递归函数抽象分析: 四.非递归归并排序的实现 1.非递归归并排序算法…...
基于SpringBoot+Html的前后端分离的学习平台
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 在知识大爆炸的现代,怎…...

MySQL实战解析底层---“order by“是怎么工作的
目录 前言 全字段排序 rowid排序 全字段排序 VS rowid排序 前言 在开发应用的时候,一定会经常碰到需要根据指定的字段排序来显示结果的需求以举例市民表为例,假设你要查询城市是“杭州”的所有人名字,并且按照姓名排序返回前1000个人的姓…...

Linux和Shell:开源力量与命令行之美
目录 一、概述二、Linux的简单介绍三、Shell的简单介绍四、Linux和Shell的应用领域五、Shell编程结语: 一、概述 Linux和Shell是开源世界中不可或缺的两个重要组成部分。Linux作为一种自由和开放的操作系统,以其稳定性、安全性和可定制性而备受推崇。而S…...
服务负载均衡Ribbon
服务负载均衡Ribbon Ribbon 介绍Ribbon 案例Ribbon 负载均衡策略Ribbon 负载均衡算法设置自定义负载均衡算法 Ribbon 介绍 Ribbon 是一个的客服端负载均衡工具,它是基于 Netflix Ribbon 实现的。它不像 Spring Cloud 服务注册中心、配置中心、API 网关那样独立部署…...

hibernate vilidator主要使用注解的方式对bean进行校验
hibernate vilidator主要使用注解的方式对bean进行校验,初步的例子如下所示: package com.learn.validate.domain; import javax.validation.constraints.Min; import org.hibernate.validator.constraints.NotBlank; public class Student { //在需要校…...
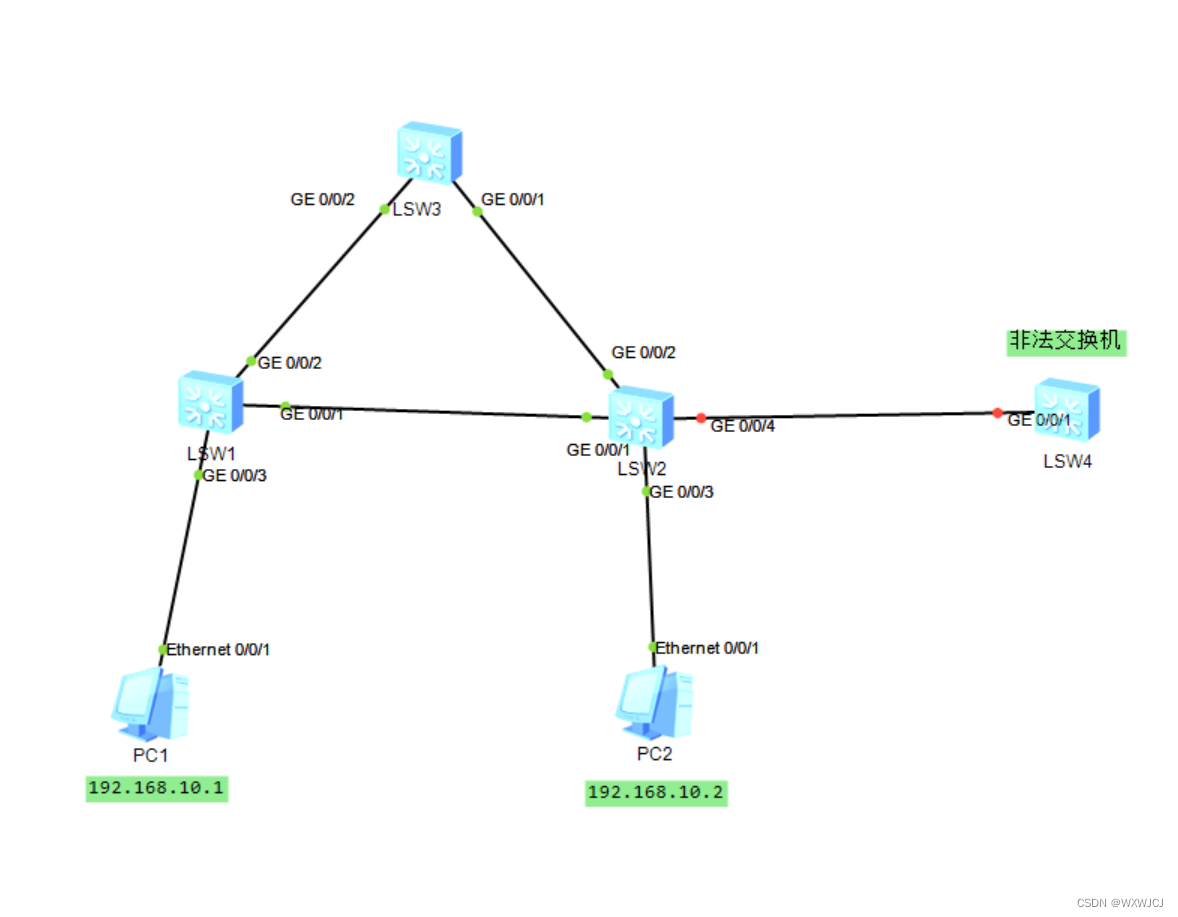
华为HCIP第一天---------RSTP
一、介绍 1、以太网交换网络中为了进行链路备份,提高网络可靠性,通常会使用冗余链路,但是这也带来了网络环路的问题。网络环路会引发广播风暴和MAC地址表震荡等问题,导致用户通信质量差,甚至通信中断。为了解决交换网…...

Jmeter(二) - 从入门到精通 - 创建测试计划(Test Plan)(详解教程)
1.简介 上一篇文章已经教你把JMeter的测试环境搭建起来了,那么这一篇我们就将JMeter启动起来,一睹其芳容,首先我给大家介绍一下如何来创建一个测试计划(Test Plan)。 2.创建一个测试计划(Test Plan&#x…...

Autosar诊断实战系列06-详解Dem中Event的NvM存储
本文框架 前言1. Dem触发NvM存储的基本流程2. Dem触发NvM存储的layout格式及内容2.1 Event在NvM中的layout格式2.2 Event在NvM中的存储内容2.3 Dem中Event与DTC的存储关系3.组合式Event(多个Event对应一个DTC)的存储处理3.1 仅分配一个Memory Entry3.2 检索方式3.3 一对一方式前…...

04 todoList案例
React全家桶 一、案例- TODO List 综合案例 功能描述 动态显示初始列表添加一个 todo删除一个 todo反选一个 todotodo 的全部数量和完成数量全选/全不选 todo删除完成的 todo 1.1 静态组件构建 将资料包中的todos_page/index.html中核心代码添加到Todo.jsx文件中,…...

海睿思分享 | 浅谈企业数据质量问题
一、数据质量问题场景 在日常工作中,业务领导经常通过BI系统来了解各项业务的业绩情况。倘若某天,他打开某张核心报表,发现当日某个区域的数据一直是空白的。BI开发人员经过几个小时的排查分析,发现是当日该区域的销售数据存在产…...

神经网络:激活函数
在计算机视觉中,激活函数是神经网络中的一种非线性函数,用于引入非线性变换和非线性特性到网络中。激活函数的作用、原理和意义如下: 1. 引入非线性变换: 神经网络的线性组合层(如卷积层和全连接层)只能表…...
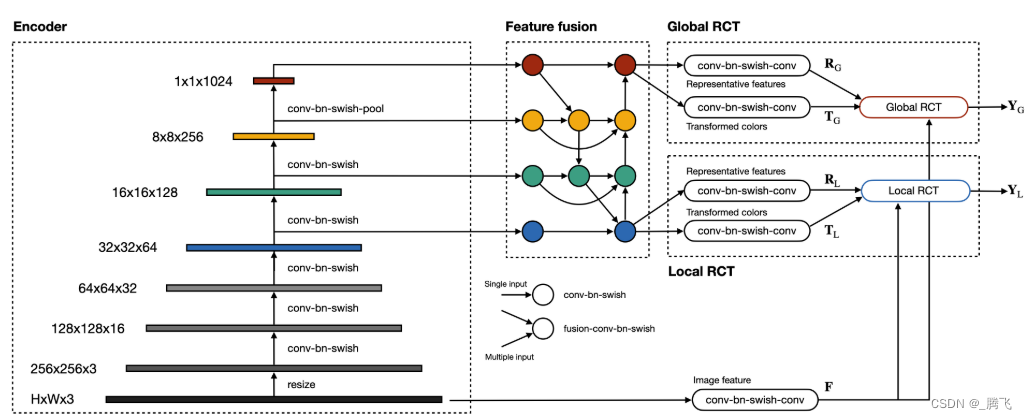
图像色彩增强相关论文阅读-Representative Color Transform for Image Enhancement(ICCV2021)
文章目录 Representative Color Transform for Image EnhancementAbstractIntroductionRelated workMethod实验Conclusion Representative Color Transform for Image Enhancement 作者:Hanul Kim1, Su-Min Choi2, Chang-Su Kim3, Yeong Jun Koh 单位:S…...
Elasticsearch介绍与应用
Elasticsearch介绍与应用 Elasticsearch的官方文档。 Elasticsearch官网参考文档:https://www.elastic.co/guide/index.html Elasticsearch官方下载地址:https://www.elastic.co/cn/downloads/elasticsearch mvnrepository依赖库地址:http…...

JavaEE规范
Servlet:用于开发 Web 应用程序的 API,定义了处理 HTTP 请求和响应的方式。JSP(JavaServer Pages):一种在服务器端生成动态网页的技术,允许将 Java 代码嵌入到 HTML 页面中。(注意JSP本质就是一个Servlet)J…...
)
嵌入式实时操作系统的设计与开发New(八)
创建线程 用户在基于RTOS开发应用程序前,首先要创建线程。 用户创建一个线程时须指定用户希望采用的调度策略。 例如,用户想创建一个周期性执行的线程: acoral_period_policy_data_t* data; data acoral_malloc(sizeof(acoral_period_poli…...

MySQL事务相关笔记
杂项 InnoDB最大特点:支持事务和行锁; MyISAM不支持事务 介绍 一个事务是由一条或者多条对数据库操作的SQL语句所组成的一个不可分割的单元,只有当事务中的所有操作都正常执行完了,整个事务才会被提交给数据库。事务有如下特性…...

如何利用AI高效率快速调色
在设计行业中,时间是非常宝贵的资源,而设计师们常常需要应对繁忙的工作日程和紧迫的截止日期。为了提高工作效率和节省时间,越来越多的设计师开始利用人工智能(AI)技术中的高效调色功能。本文将介绍如何利用AI高效率快…...
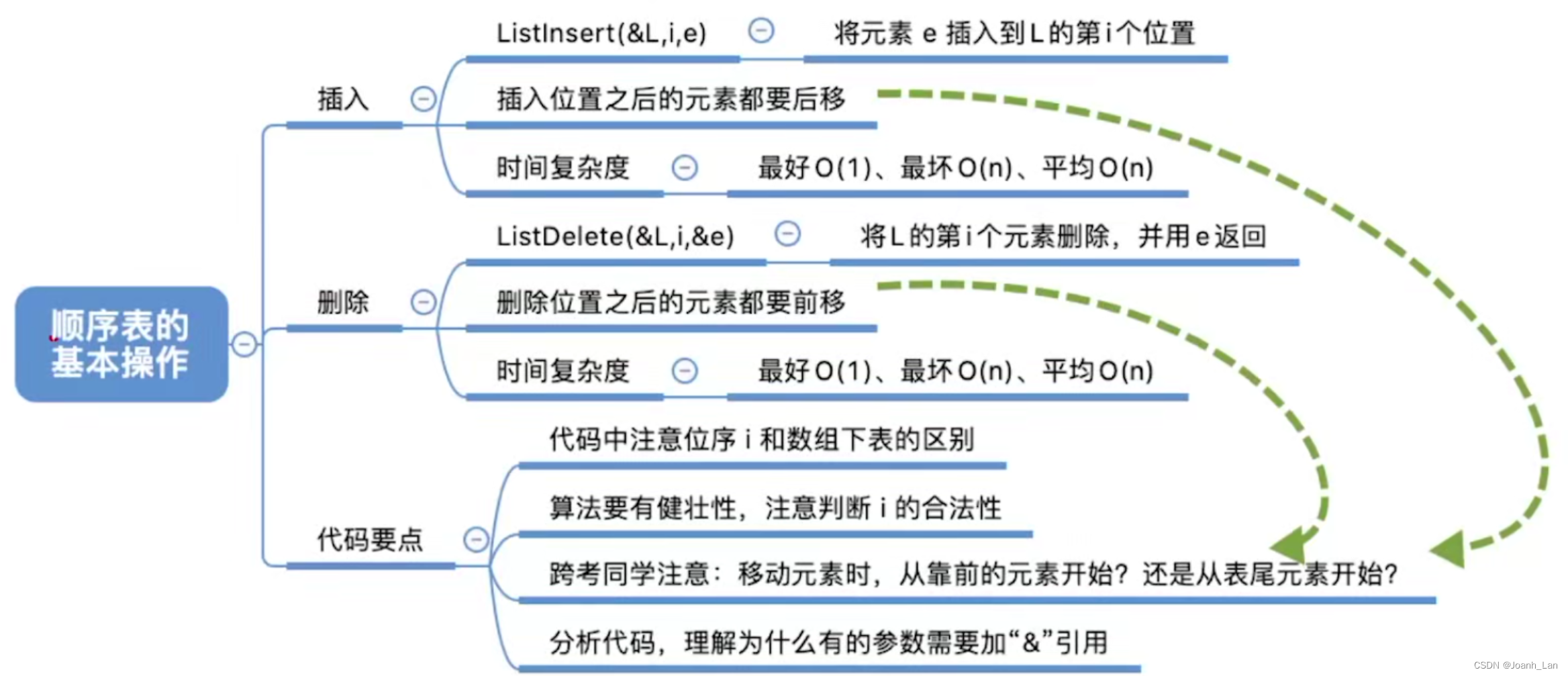
数据结构--顺序表的基本操作--插入 and 删除
数据结构–顺序表的基本操作–插入 顺序表的插入操作 实现目标 ListInsert(&L,i,e):插入操作。在表L中的第i个位置上插入指定元素e。 typedef struct {int data[MaxSize];int len; }Sqlist;代码实现: #include <stdio.h> #include <stdlib.h> …...

BCSP-玄子Java开发之Java Web编程CH01_初识动态网页
BCSP-玄子Java开发之Java Web编程CH01_初识动态网页 1.1 B/S架构 B/S架构:浏览器/服务器 程序完全部署在服务器上使用浏览器访问服务器无需单独安装客户端软件 为什么要使用B/S架构 B/S与C/S比较B/S架构C/S架构软件安装浏览器需要专门的客户端应用升级维护客户…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...