【C++】二叉搜索树的实现(递归和非递归实现)
文章目录
- 1、二叉搜索树
- 1.1 构建二叉搜索树
- 1.2 二叉搜索树的插入
- 1.3 二叉搜索树的删除
- 1.4 二叉搜索树插入和删除的递归实现
为了学习map和set的底层实现,需要知道红黑树,知道红黑树之前需要知道AVL树。
红黑树和AVL树都用到了二叉搜索树结构,所以先谈谈二叉搜索树。
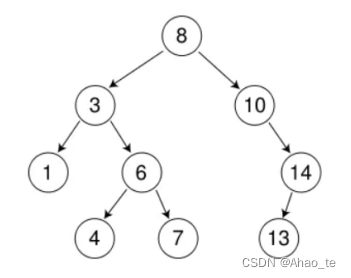
1、二叉搜索树
二叉搜索树(Binary Search Tree)也称二叉排序树,它最重要的是能给数据排序以及去重。
其性质:
- 若左子树不为空,左子树的键值都小于根以及右子树。
- 若右子树不为空,右子树的键值都大于根以及左子树。
- 二叉搜索树的子树都是二叉搜索树。
二叉搜索树顾名思义,根据其特性可以很方便让我们搜索一个值。
二叉树的中序遍历就是一个排序。
二叉搜索树的结点没有相同的值。
值得注意的是:
- 二叉搜索树没有要求严格平衡,所以查找一个值的时间复杂度最坏可能是O(N)(成为单枝树,就是一个链表。)
- 二叉搜索树不支持值修改,因为会打乱树的结构。
1.1 构建二叉搜索树
在二叉树的模型中,有K模型和KV模型,就是一个结点一个值和一个结点一个键值对两个模型。
一个值的很简单,而KV模型就是一个结点存放一个key和一个value。
下面实现的是KV模型的基本框架
#include <iostream>
#include <assert.h>
#include <string>
using namespace std;template<class K, class V>
struct BSTreeNode
{//设置成三叉链的结构,让子树能方便访问根结点struct BSTreeNode<K, V>* _left;struct BSTreeNode<K, V>* _right;struct BSTreeNode<K, V>* _parent;K _key;V _value;//构造BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _parent(nullptr), _key(key), _value(value){}
};template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:
private:Node* _root = nullptr;
};
1.2 二叉搜索树的插入
二叉树插入很简单。
1、如果树是空,直接创建结点返回。
2、树不为空,根据搜索树的特性通过值的大小确定应该放在左还是右子树,如果到达空结点,那么就到达该放的位置。
3、确认好放的位置,因为需要链接,所以需要有一个parent能指向上一个结点。通过上一个结点和新结点的大小判断应该链接在哪边。
4、因为设计的是三叉链结构,所以最后还得指向父节点。
bool Insert(const K& key, const V& value){ //树为空if (_root == nullptr){_root = new Node(key, value);return true;}Node* cur = _root;Node* parent = _root;//找到新结点应该放的位置while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//如果值相同直接返回return false;}}//确认好位置后,父子结点互相链接cur = new Node(key, value);if (parent->_key < cur->_key){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}return true;}
1.3 二叉搜索树的删除


bool Erase(const K& key){//空树返回if (_root == nullptr){return false;}Node* cur = _root;Node* parent = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//先找到需要删的结点//删的结点左为空if (cur->_left == nullptr){//删的结点为根节点情况if (parent == cur){_root = cur->_right;}else{//需要确定父节点哪边指向curif (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}delete cur;}else if (cur->_right == nullptr){//删的结点右为空//删的结点为根节点情况if (parent == cur){_root = cur->_left;}else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}delete cur;}else{//左右都不为空,替换右子树最小的Node* minRight = cur->_right;while (minRight->_left){minRight = minRight->_left;}cur->_key = minRight->_key;cur->_value = minRight->_value;parent = minRight->_parent;//需要确定父节点哪边指向minRightif (parent->_right == minRight){parent->_right = minRight->_right;}else{parent->_left = minRight->_right;}//因为值交换了,所以删除右子树最小结点delete minRight;} //elsereturn true;} //else} // whilereturn false;} //Erase
1.4 二叉搜索树插入和删除的递归实现
有一点必须明确的是,非递归一定是比递归要好的,这里实现递归只是练习,增强代码能力。
首先是InOrder()方法的实现,当调用的方法是不含参数的,实现又需要有参数的,就可以再嵌套一层,并且_InOrder(Node* root)不想提供给类外调用,就可以放在私有域。
...
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:bool Insert(const K& key, const V& value){}bool Erase(const K& key){}void InOrder(){_InOrder(_root);}
private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}Node* _root = nullptr;
};
插入的递归实现
插入递归很简单,值得说的是,通过给root添加引用,能很方便的将新结点链接起来。
...
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:...bool Insert(const K& key, const V& value){return _InsertR(_root, key, value);}bool Erase(const K& key){}...
private:...bool _InsertR(Node*& root, const K& key, const V& value){if (root == nullptr){//因为需要对root修改,所以在参数部分需要对root添加引用(Node*& root)root = new Node(key, value);return true;}if (root->_key < key){_InsertR(root->_right, key, value);}else if (root->_key > key){_InsertR(root->_left, key, value);}else{return false;}}Node* _root = nullptr;
};
删除的递归实现
删除的思路整体上和非递归差不多,不同的是。
1、因为删除需要改变树的结构,肯定是要改变每次递归的根节点的,所以需要传引用。
2、删除的思路是和右子树最小结点值交换后,删除最小结点。需要往右找到最小结点。
...
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:bool Erase(const K& key){_EraseR(_root, key);}
private:
...bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if(root->_key > key){return _EraseR(root->_left, key);}else{//找到删除的结点Node* del = root;if (root->_left == nullptr){//左边为空//因为要改变树的结构,改变root,所以root得加&//引用加完后,改变root也代表着改变父结点的指向//所以就是父节点指向root的指向变成指向root的右子树root = root->_right;}else if (root->_right == nullptr){//右边为空root = root->_left;}else{Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}swap(root->_key, minRight->_key);// 转换成子树中去删除节点// 因为和最小节点的值交换后,原本root的值成了最小值// 再凭借key去查找最小值的结点删// 最小节点左边一定为空_EraseR(root->_right, key);}delete del;return true;} //else}Node* _root = nullptr;
};
本章完~
相关文章:

【C++】二叉搜索树的实现(递归和非递归实现)
文章目录1、二叉搜索树1.1 构建二叉搜索树1.2 二叉搜索树的插入1.3 二叉搜索树的删除1.4 二叉搜索树插入和删除的递归实现为了学习map和set的底层实现,需要知道红黑树,知道红黑树之前需要知道AVL树。 红黑树和AVL树都用到了二叉搜索树结构,所…...

春招来了,如何正确使用领英超高效招聘海外员工、挖掘人才?
金三银四到了,每年的这个时候都是企业招聘的好时机。而领英是目前全球最大的职场社交网络平台,基本上海外求职都是在使用它,所以很多企业涉及到海外招聘时,都会优先考虑领英,但是却经常缺乏一些经验技巧,今…...

Mysql中锁机制深入理解
Mysql中锁机制深入理解默认大家已经知道。分类性能悲观锁,乐观锁操作类型读锁,写锁,数据粒度表锁,行锁,页面锁更细粒度间隙锁,临键锁按使用来讲。由数据粒度出发。表锁,分为 共享锁,…...

去中心化社交网络协议除了Nostr还有哪些?
当下最火的去中心化社交软件Dmaus就是基于Nostr协议开发的,Nostr协议的基本情况之前的文章《一文了解去中心化社交网络协议Nostr》已经做了详细介绍,本文将介绍其他几个目前比较流行的去中心化社交协议。FarcasterFarcaster是由前Coinbase高管Dan Romero…...

【FT2000/4+X100】调试记录
订阅专栏 硬件环境FT2000/4+X100,单板结构,对外显示,运行银行麒麟操作系统。 一 生成UEFI.BIN,烧写在FT2000-4的QSPI Flash中 1 2 下载源文件 edk2-for-support.tar; 参考文件 ft2004c&D2000编译打包说明V1.0.5; 解压源文件; 根目录下 build2004C.sh为四核产品…...
我的Android启动优化—【黑白屏优化】
简述 在Android App使用过程中,对于应用的优化是一个加分项,举个例子,打开你的App需要2秒,人家0.5秒,这就是很大的用户体验上的优化。 问题的产生 在开发中,我们在启动app的时候,屏幕会出现一…...

TongWeb8编码设置说明
应用场景:在遇到中文问题时,常需要通过设置编码格式来解决问题。下面介绍TongWeb8的编码设置及优先级。一、web.xml中请求、响应编码的配置优先级最高在JavaEE8规范中web.xml增加了request, response编码配置,该配置优先级最高。<?xml ve…...

不同相机之间图片像素对应关系求解(单应性矩阵求解)
一、场景 相机1和相机2相对位置不变,相机拍摄图片有重叠,求他们交叠部分的一一对应关系。数学语言描述为已知相机1图片中P点像素(u1, v1),相机1中P点在相机2图片中像素值为(u2, v2),它们存在某种变换,求变换矩阵。 因为…...

远程管理时代,还得是智能化PDU才靠得住!
在如今这个信息技术高速发展的时代,数据中心IDC机房服务器数量与日俱增,提供DNS域名服务、主机托管服务、虚拟主机服务等服务的服务器是IDC最基本的功能之一。服务器需要7*24小时不间断持续工作,但当服务器数量很大,服务器工作、重…...
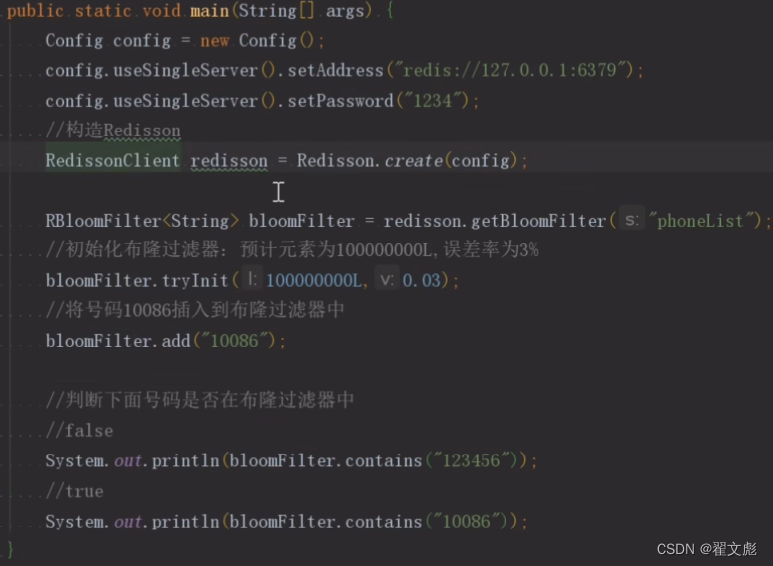
通俗易懂理解——布隆过滤器
文章目录概述本质优缺点优点:缺点:实际应用解决redis缓存穿透问题:概述 本质 本质:很长的二进制向量(数组) 主要作用:判断一个数据在这个数组中是否存在,如果不存在为0,…...

TypeScript 学习之类型推导
在一些情况下,代码上没有显性明确类型,typescript 可以隐形推断出类型。 基础 let x 3;变量x的类型被推断为数字。 类型推断发生在初始化变量和成员,设置默认参数值和决定函数返回值时 最佳通用类型 let x [0, 1, null]; // 类型为 numb…...

Android四大组件——Service详解
Service 为后台运行,不可见,没有界面。优先级高于Activity(内存不足时先杀掉Activity),运行在主线程且不能做耗时操作。 一、Service 启动方式 1、startService() 通过 startService 启动后,service会一直…...

svg转png
svg转png写了一个spring boot项目,支持传入svg文件转出png图片,并且自定义转出png的宽和高。主要代码如下:所需依赖如下:演示如下:首先,运行项目使用接口调用工具调用接口发送请求,提取文件1000…...

教你如何搭建人事OA-员工管理系统,demo可分享
1、简介1.1、案例简介本文将介绍,如何搭建人事OA-员工管理。1.2、应用场景人事OA-员工管理应用对员工信息进行管理,可办理入职、转正、离职等流程。2、设置方法2.1、表单搭建1)新建表单【员工管理】,字段设置如下:名称…...

C++递推基础知识
文章目录一、递推的概念二、递推和递归的区别三、递推的实例1、最基础的:斐波那契数列2、变形版斐波那契数列3、较复杂的递推式求解:昆虫繁殖4、经典逆推问题:题目数量一、递推的概念 1、什么是递推算法? 递推算法:是…...

【Python入门第十天】Python 布尔
布尔表示两值之一:True 或 False。 布尔值 在编程中,通常需要知道表达式是 True 还是 False。 可以计算 Python 中的任何表达式,并获得两个答案之一,即 True 或 False。 比较两个值时,将对表达式求值,P…...
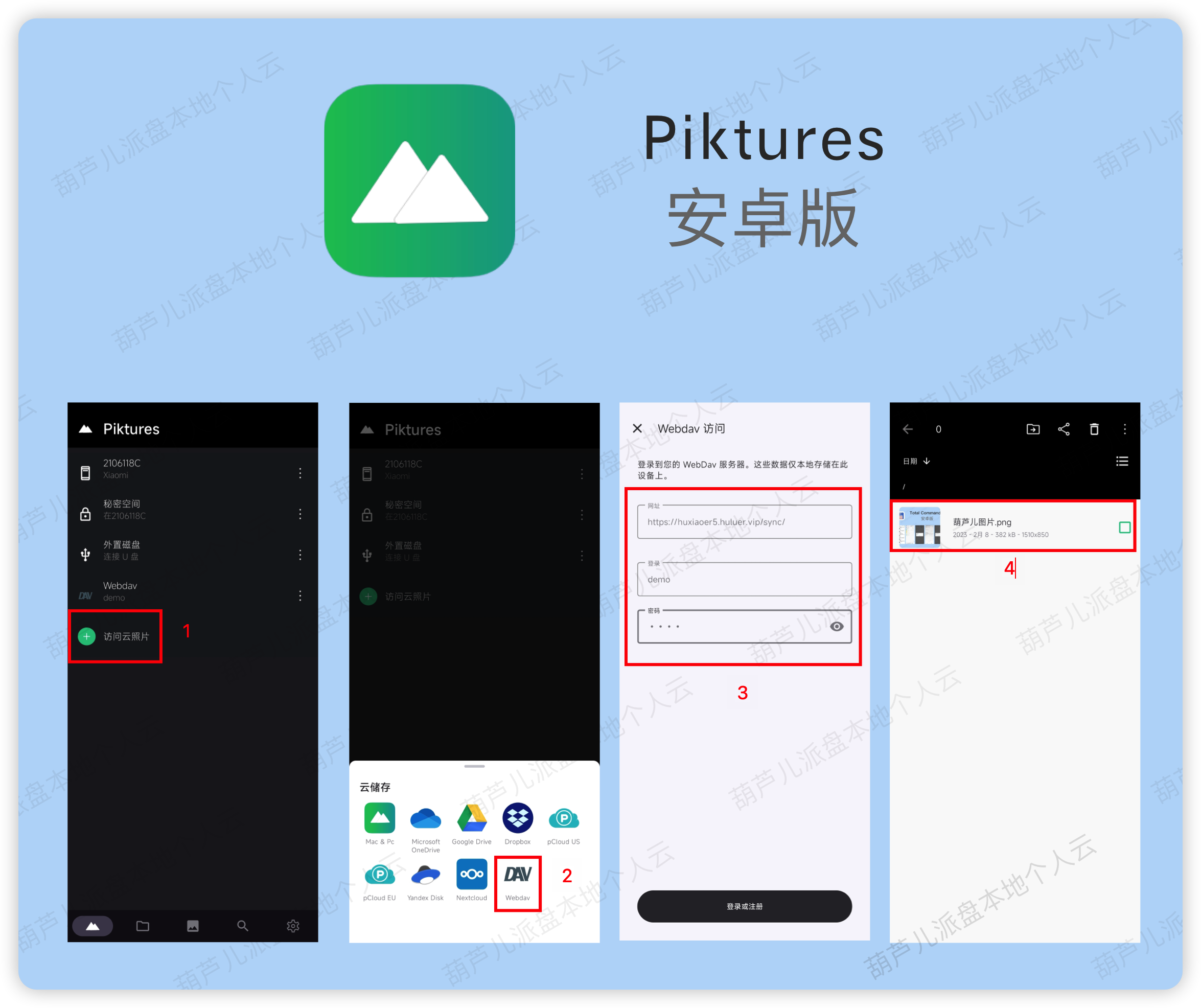
WebDAV之π-Disk派盘+Piktures
Piktures支持WebDAV方式连接π-Disk派盘。推荐一款简单易用,功能超级强大的智能相册应用。Piktures智能相册是一款简单易用,功能超级强大的智能相册应用,它不仅可以访问本地和云照片,还可以照片编辑器,而且它同时还是一…...
Revit问题:Navisworks中导入的rvt模型角度不正确调整
一、Navisworks中导入的rvt模型角度不正确调整方法 通常情况下,我们做好一个Revit模型,有时候出于成果保护或者鉴于Revit自带的碰撞检测效果不够直观、Revit模型体量太大,需要一个轻量化的模型展示,我们通常情况下会使用Autodesk公…...

最全正则验证
一、校验数字的表达式 1. 数字:^[0-9]*$ 2. n位的数字:^\d{n}$ 3. 至少n位的数字:^\d{n,}$ 4. m-n位的数字:^\d{m,n}$ 5. 零和非零开头的数字:^(0|[1-9][0-9]*)$ 6. 非零开头的最多带两位小数的数字:…...
阿里云服务器入门使用流程 新手学习教程
一、阿里云根据个人需要选合适的云服务器,选好cpu、内存、带宽,地域,这四个是主要的。其他可以默认选择。 二、登陆控制台 输入账号密码,进去看到服务界面,新手可能不容易看懂。点击左侧菜单,点击云服务器…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
