[Datawhale][CS224W]图机器学习(三)
目录
- 一、简介与准备
- 二、教程
- 2.1 下载安装
- 2.2 创建图
- 2.2.1 常用图创建(自定义图创建)
- 1.创建图对象
- 2.添加图节点
- 3.创建连接
- 2.2.2 经典图结构
- 1.全连接无向图
- 2.全连接有向图
- 3.环状图
- 4.梯状图
- 5.线性串珠图
- 6.星状图
- 7.轮辐图
- 8.二项树
- 2.2.3 栅格图
- 1.二维矩形栅格图
- 2.多维矩形栅格图
- 3.二维三角形栅格图
- 3.二维六边形栅格图
- 4.n维超立方体图
- 2.2.4 NetworkX内置图
- 1.钻石图
- 2.牛角图
- 3.荔枝图?(虽然看不出跟荔枝有啥联系)
- 4.房子图
- 5.房子x图
- 6.风筝图
- 2.2.5 随机图
- 2.2.6 无标量有向图
- 2.2.7 社交网络
- 1.空手道俱乐部数据集
- 2.雨果《悲惨世界》任务关系
- 3.家庭关系图
- 2.2.8 社群聚类图
- 2.2.9 树结构
- 2.3 常用信息获取
- 2.4 图可视化
- 2.4.1 初始化
- 2.4.2 原生可视化
- 2.4.3 不显示节点
- 2.4.4 设置颜色
- 2.4.5 无向图转有向图后显示
- 2.4.6 通过设置每个节点的坐标来显示图
- 2.4.7 绘制房子图(例子)
- 2.4.8 可视化模板(重要)
- 2.4.9 自我中心图(ego图)
- 2.5 图相关数据分析
- 2.5.1 计算PageRank节点重要度
- 2.5.2 最大连通域子图
- 2.5.3 每个节点的连接数(degree)
- 2.5.4 一些可能用到的图的基础数据
- 2.5.5 节点特征(重要)
- 2.5.6 计算全图的Graphlet
- 参考文献
Datawhale开源学习社区 x 同济子豪兄 Stanford课程中文精讲系列笔记
本文同时发布在:本人博客https://wumorfr.github.io/
一、简介与准备
NetworkX用于实现创建,操作和研究复杂网络的结构,动态功能
几个常用链接
- NetworkX 主页
- NetworkX 文档
- NetworkX 文档 PDF
本文接下来使用环境包括
import networkx
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib as mpl
import pandas as pd
import matplotlib.colors as mcolors# %matplotlib inline #anconda中使用时要添加# windows系统
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示正负号
二、教程
2.1 下载安装
本人是使用pip安装(使用了清华源)
pip install networkx -i https://pypi.tuna.tsinghua.edu.cn/simple
安装好后可在python环境下运行
import networkx as nxprint("nx.__version__: " + nx.__version__)
进行校验输出,结果类似如下

2.2 创建图
本列表中2.2.2至2.2.9暂时视为不常用,因为本人初学使用时基本很少看到,了解即可,可视作资料库,用的时候再查。不过2.2.7中数据集有的时候会用可以多看两眼(笑)
2.2.1 常用图创建(自定义图创建)
1.创建图对象
G = nx.Graph() # 空无向图 (重要)
G = nx.DiGraph() # 空有向图 (重要)
G = nx.MultiGraph() # 空多重无向图
G = nx.MultiDigraph() # 空多重有向图
G.clear() # 清空图
2.添加图节点
此处先创建一个无节点无连接的空图G和另一个首尾相连成串的Path Graph H
G =nx.Graph()
H =nx.path_graph(10)
G.add_node('刘备') # 添加单个节点
G.add_nodes_from(['诸葛亮','曹操']) # 三、添加多个节点
G.add_nodes_from([('关羽',{'武器':'青龙偃月刀','武力值':90,'智力值':80}),('张飞',{'武器':'八丈蛇矛','武力值':85,'智力值':75}),('吕布',{'武器':'方天画戟','武力值':100,'智力值':70})
]) # 添加带属性的节点G.add_nodes_from(H) # 将H的节点添加到G中
print("G.nodes",G.nodes)
print("G.len",len(G))G.add_node(H) # 将H本身作为一个节点添加进G中
print("G.nodes",G.nodes)
print("G.len",len(G))
结果:

注意:
add_node和add_nodes_from
对于add_node加一个点来说,字符串是只添加了名字为整个字符串的节点。但是对于add_nodes_from加一组点来说,字符串表示了添加了每一个字符都代表的多个节点,exp:
g.add_node("spam") #添加了一个名为spam的节点
g.add_nodes_from("spam") #添加了4个节点,名为s,p,a,m
小结
节点可以为任意可哈希的对象,比如字符串、图像、XML对象,甚至另一个Graph、自定义的节点对象
通过这种方式可以根据自己的使用灵活的自由构建:以图、文件、函数为节点等灵活的图的形式
3.创建连接
此处先创建无向空图G和有向空图H
# 创建无向空图G = nx.Graph()
print(G.is_directed())
# 给整张图添加属性特征
G.graph['Name'] = "HelloWord"
print(G.graph)
# 创建有向空图
H = nx.DiGraph()
print(H.is_directed())
输出:


G.add_node(0,feature=5,label=0,zihao=2) # 创建单个节点,此处为创建0号节点,并添加特征属性
G.add_nodes_from([(1,{'feature':1,'label':1,'zihao':3}),(2,{'feature':2,'label':2,'zihao':4})
]) # 创建多个节点
全图节点信息:
print(G.number_of_nodes())
print(G.nodes)
print(G.nodes(data=True))# 遍历所有节点,data=True表示输出节点特征属性信息
for node in G.nodes(data=True):print(node)

此时点均为散点,后创立连接
G.add_edge(0,1,weight=0.5,like=3) # 创建单个连接,设置属性特征
G.add_edges_from([(1,2,{'weight':0.3,'like':5}),(2,0,{'weight':0.1,'like':8})
]) # 创建多个连接
连接情况
全图连接信息
print(G.number_of_nodes())
print(G.size())
print(G.edges())
print(G.edges(data=True))# 遍历所有连接,data=True表示输出连接特征属性信息
for edge in G.edges(data=True):print(edge)

查询节点的连接数
- 指定节点
node_id=1
print(G.degree[node_id])
- 指定节点的所有相邻节点
for neighbor in G.neighbors(node_id):print("Node {} has neighbor {}".format(node_id,neighbor))

- 所有节点
for node_id in G.nodes():for neighbor in G.neighbors(node_id):print("Node {} has neighbor {}".format(node_id,neighbor))

2.2.2 经典图结构
1.全连接无向图
G = nx.complete_graph(7)
nx.draw(G)
plt.show()
# 全图连接数
print("全图连接数:", G.size())
2.全连接有向图
G = nx.complete_graph(7, nx.DiGraph())
nx.draw(G)
plt.show()# 是否是有向图
print("是否是有向图:", G.is_directed())
3.环状图
G = nx.cycle_graph(5)
nx.draw(G)
plt.show()
4.梯状图
G = nx.ladder_graph(5)
nx.draw(G)
plt.show()
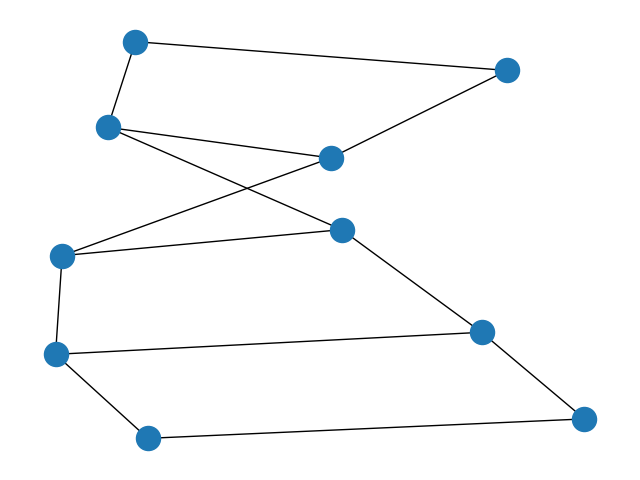
5.线性串珠图
G = nx.path_graph(15)
nx.draw(G)
plt.show()
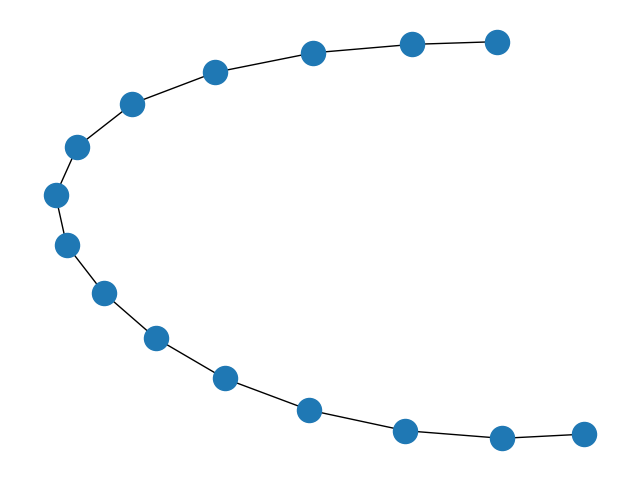
6.星状图
G = nx.star_graph(7)
nx.draw(G)
plt.show()
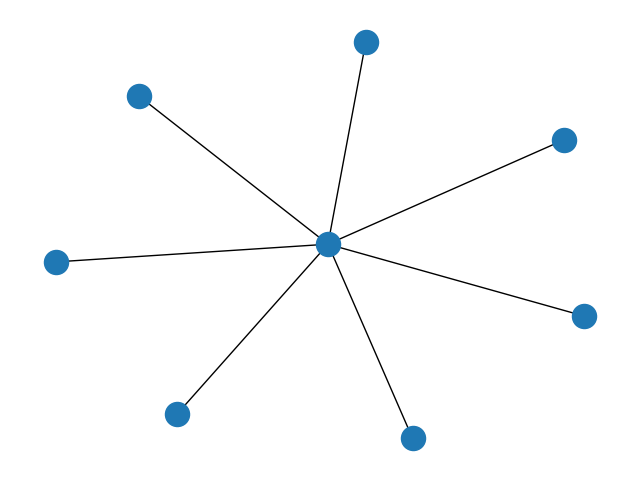
7.轮辐图
G = nx.wheel_graph(8)
nx.draw(G)
plt.show()
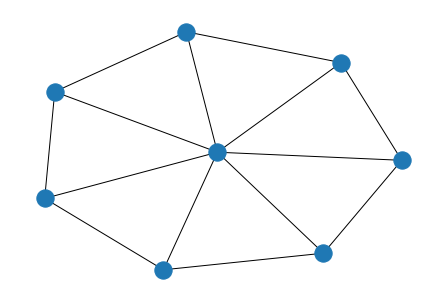
8.二项树
G = nx.binomial_tree(5)
nx.draw(G)
plt.show()
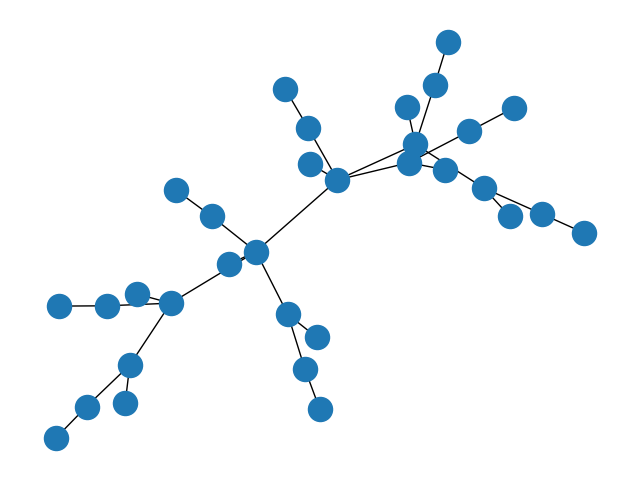
2.2.3 栅格图
1.二维矩形栅格图
G = nx.grid_2d_graph(3, 5)
nx.draw(G)
plt.show()
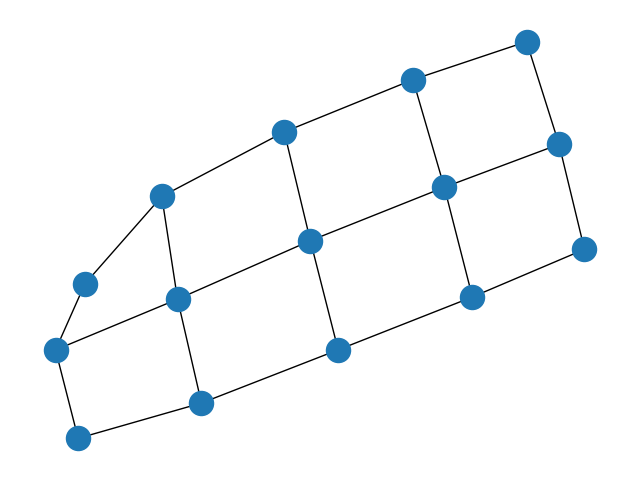
2.多维矩形栅格图
G = nx.grid_graph(dim=(2, 3, 4))
nx.draw(G)
plt.show()
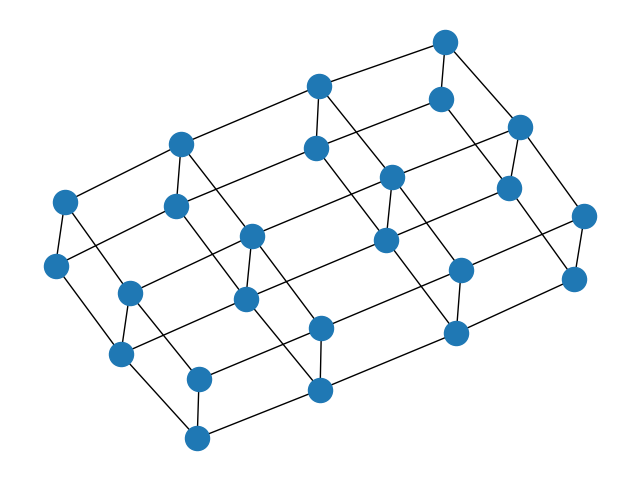
3.二维三角形栅格图
G = nx.triangular_lattice_graph(2, 5)
nx.draw(G)
plt.show()
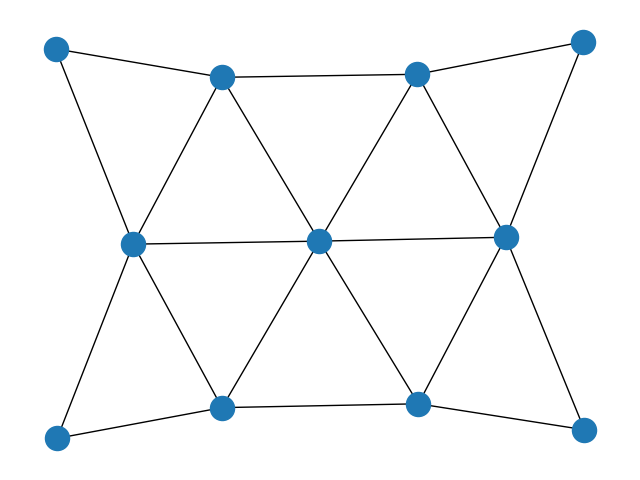
3.二维六边形栅格图
G = nx.hexagonal_lattice_graph(2, 3)
nx.draw(G)
plt.show()
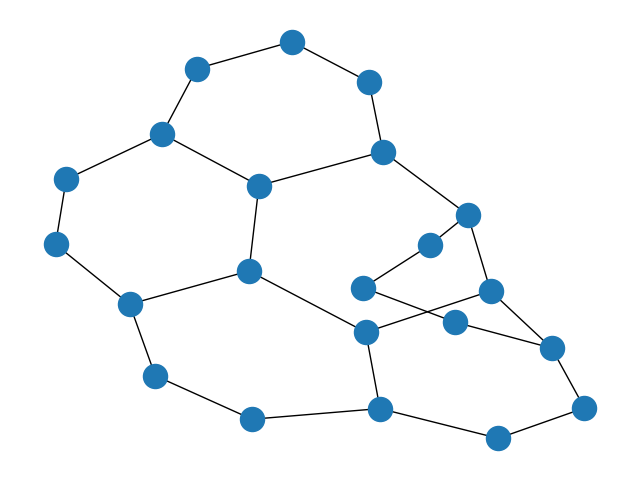
4.n维超立方体图
G = nx.hypercube_graph(4)
nx.draw(G)
plt.show()
2.2.4 NetworkX内置图
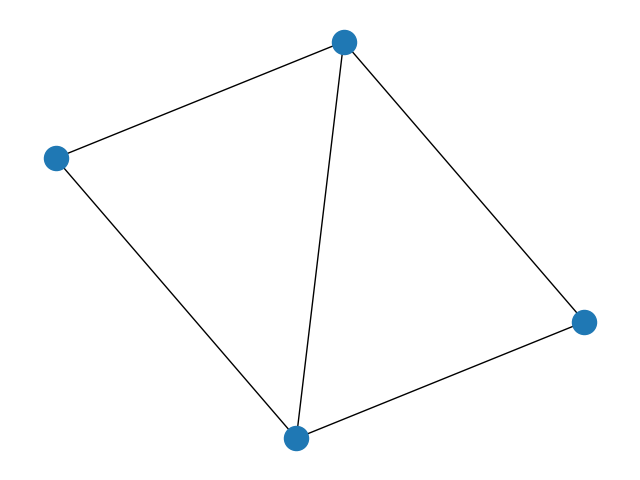
1.钻石图
G = nx.diamond_graph()
nx.draw(G)
plt.show()
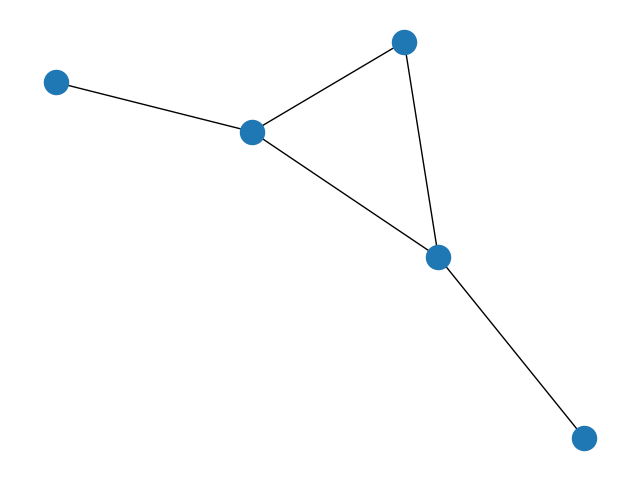
2.牛角图
G = nx.bull_graph()
nx.draw(G)
plt.show()
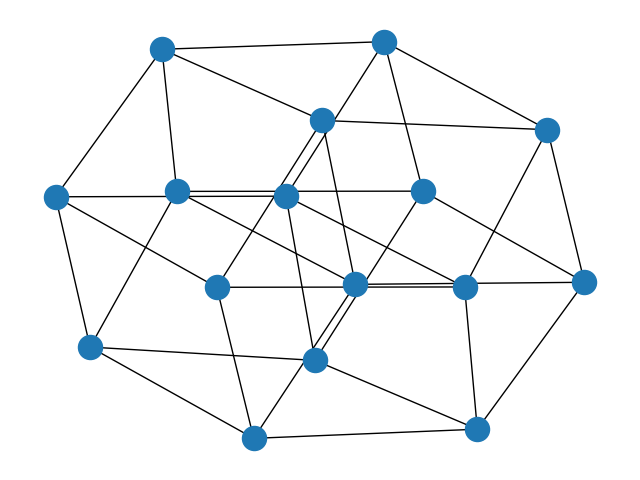
3.荔枝图?(虽然看不出跟荔枝有啥联系)
G = nx.frucht_graph()
nx.draw(G)
plt.show()
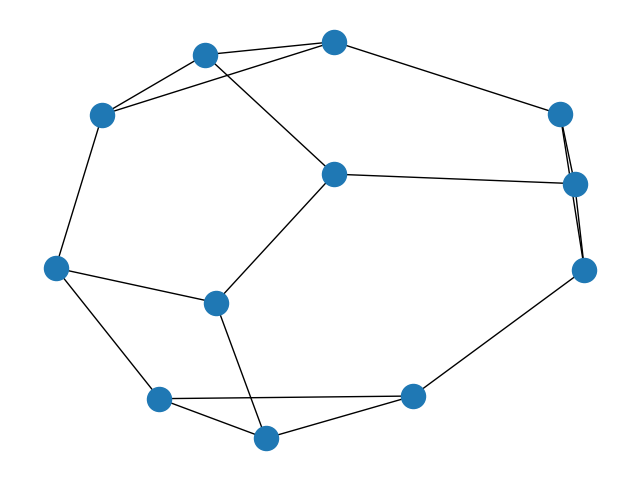
4.房子图
G = nx.house_graph()
nx.draw(G)
plt.show()
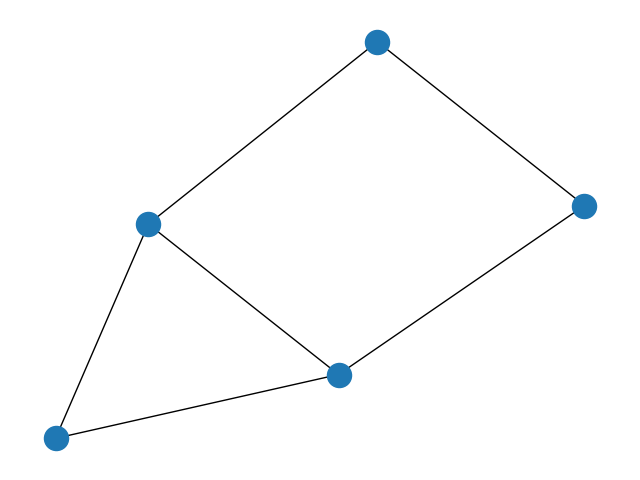
5.房子x图
G = nx.house_x_graph()
nx.draw(G)
plt.show()
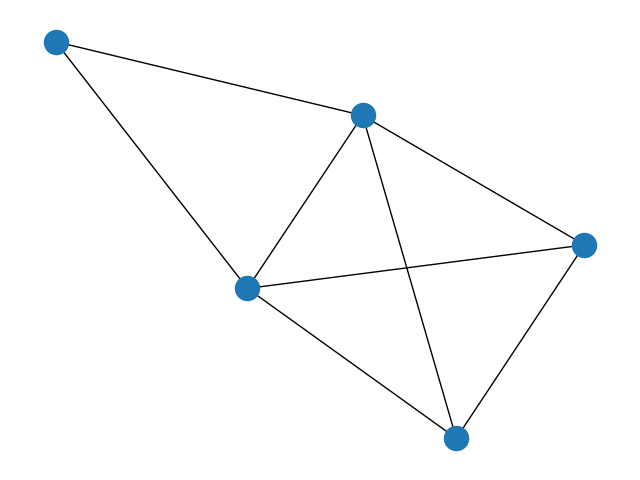
6.风筝图
G = nx.krackhardt_kite_graph()
nx.draw(G)
plt.show()
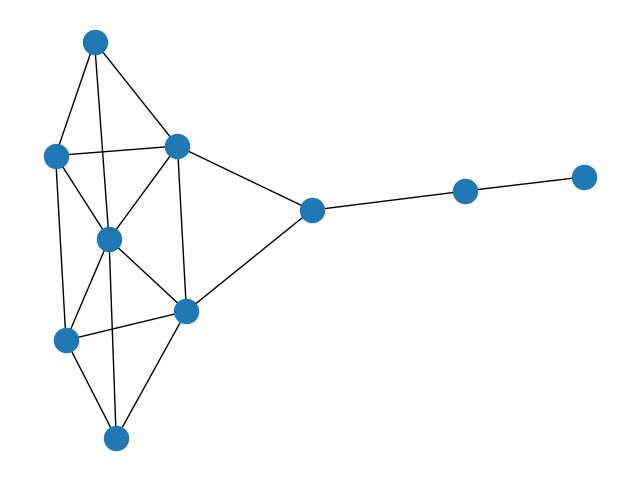
2.2.5 随机图
G = nx.erdos_renyi_graph(10, 0.5)
nx.draw(G)
plt.show()
2.2.6 无标量有向图
G = nx.scale_free_graph(100)
nx.draw(G)
plt.show()
2.2.7 社交网络
1.空手道俱乐部数据集
G = nx.karate_club_graph()
nx.draw(G, with_labels=True)
plt.show()
print(G.nodes[5]["club"])
print(G.nodes[9]["club"])
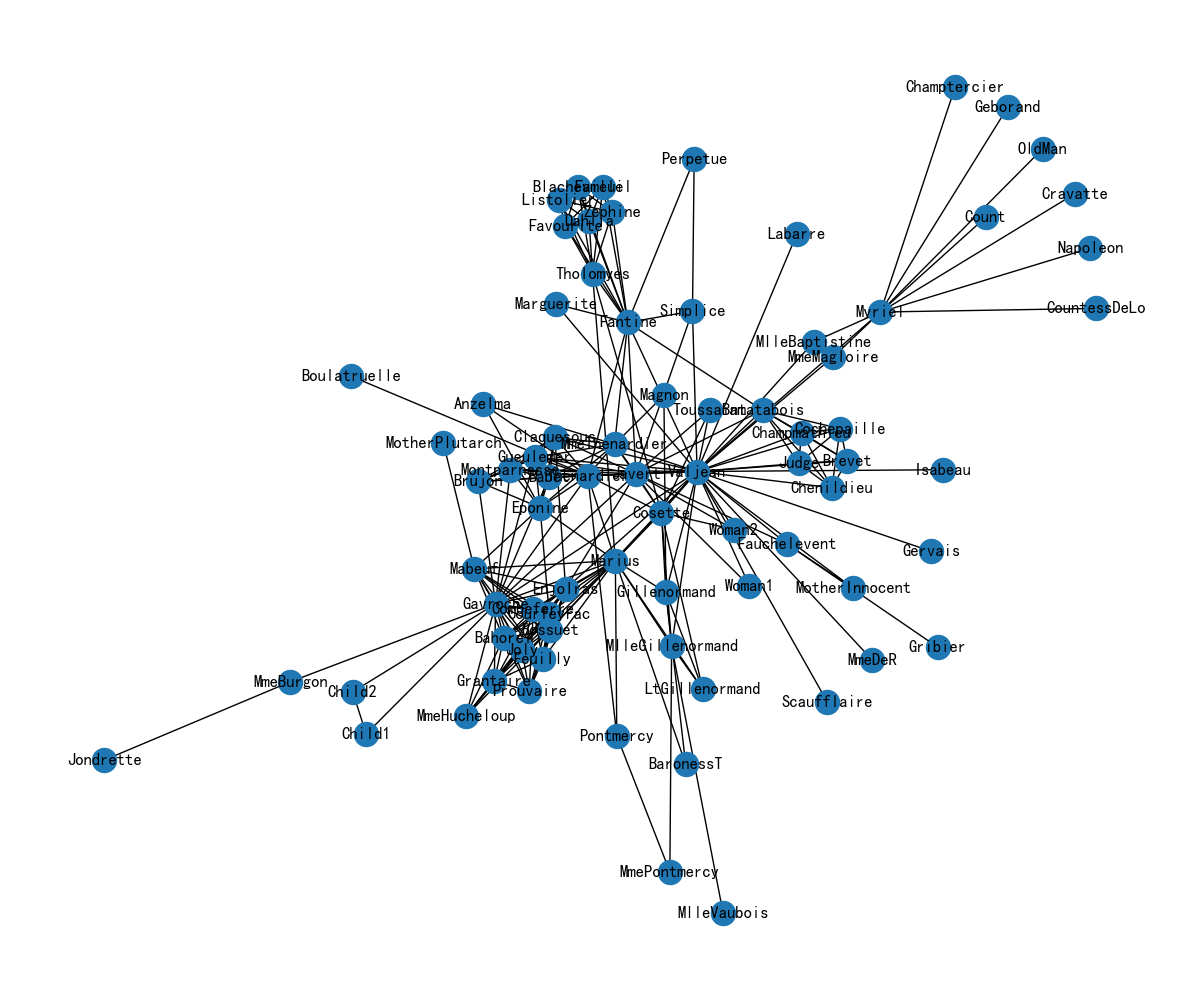
2.雨果《悲惨世界》任务关系
G = networkx.les_miserables_graph()
plt.figure(figsize=(12, 10))
pos = nx.spring_layout(G, seed=10)
nx.draw(G, pos, with_labels=True)
plt.show()
plt.show()
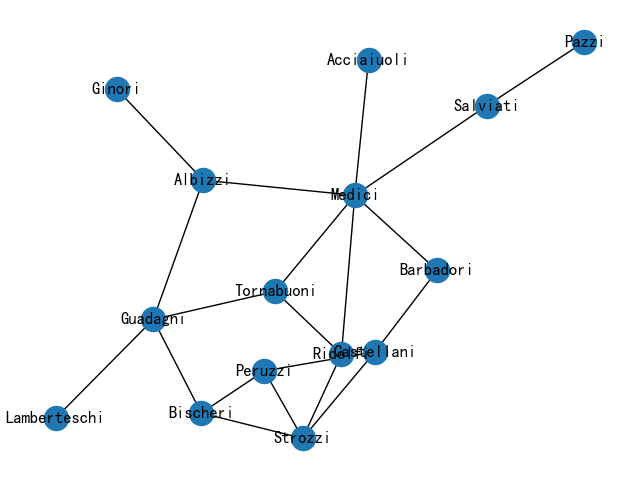
3.家庭关系图
G = nx.florentine_families_graph()
nx.draw(G, with_labels=True)
plt.show()
2.2.8 社群聚类图
G = nx.caveman_graph(4, 3)
nx.draw(G, with_labels=True)
plt.show()
2.2.9 树结构
tree = nx.random_tree(n=10, seed=0)
print(nx.forest_str(tree, sources=[0]))
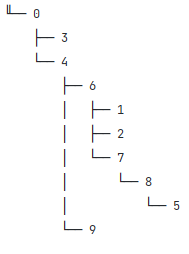
2.3 常用信息获取
nx.info(G) # 图信息的概览
G.number_of_nodes()
G.number_of_edges()# 获取和节点idx连接的边的attr属性之和
G.in_degree(idx, weight='attr')# 如果想知道某个结点相连的某个边权之和:
DG.degree(nodeIdx, weight='weightName')# 获取结点或者边的属性集合,返回的是元组的列表
G.nodes.data('attrName')
G.edges.data('attrName')# 获取n1 n2的边的length权重,那么:
G[n1][n2]['length']# 如果是有重边的图,选择n1,n2第一条边的length权重,则:
G[n1][n2][0]['length']# 获取n1结点的所有邻居
nx.all_neighbors(G, n1)# 判断图中n1到n2是否存在路径
nx.has_path(G, n1, n2)# 根据一个结点的list,获取子图
subG = nx.subgraph(G, nodeList)
2.4 图可视化
2.4.1 初始化
创建4*4网格图(无向图)
G = nx.grid_2d_graph(4,4)
2.4.2 原生可视化
pos = nx.spring_layout(G,seed=123)
nx.draw(G,pos)
plt.show()
2.4.3 不显示节点
nx.draw(G,pos,node_size=0,with_labels=False)
plt.show()
2.4.4 设置颜色
print(len(G.edges()))
nx.draw(G,pos,node_color = '#66ccff', # 节点颜色edgecolors='red', # 节点外边缘颜色edge_color='blue', # edge的颜色# edge_cmap=plt.cm.coolwarm,# 配色方案node_size=800,with_labels=False,width=3,
)
plt.show()
2.4.5 无向图转有向图后显示
nx.draw(G.to_directed(), # 关键是这一句pos,node_color = '#66ccff', # 节点颜色edgecolors='red', # 节点外边缘颜色edge_color='tab:gray', # edge的颜色# edge_cmap=plt.cm.coolwarm,# 配色方案node_size=800,with_labels=False,width=3,arrowsize=10,
)
plt.show()
2.4.6 通过设置每个节点的坐标来显示图
# 无向图
# 初始化图
G = nx.Graph()
G.add_edge(1,2)
G.add_edge(1,3)
G.add_edge(1,5)
G.add_edge(2,3)
G.add_edge(3,4)
G.add_edge(4,5)
nx.draw(G,with_labels=True)
plt.show()# 关键代码
# 设置每个节点可视化的坐标
pos={1:(0,0),2:(-1,0.3),3:(2,0.17),4:(4,0.255),5:(5,0.03)}# 设置其他可视化格式
options = {"font_size":36,"node_size":3000,"node_color":"white","edgecolors":"black","linewidths":5, # 节点线宽"width": 5, # edge线宽
}nx.draw_networkx(G,pos,**options)ax=plt.gca()
ax.margins(0.20) # 在图的边缘留白,防止节点被截断
plt.axis("off")
plt.show()# 有向图
G = nx.DiGraph([(0,3),(1,3),(2,4),(3,5),(3,6),(4,6),(5,6)])
nx.draw(G,with_labels=True)
plt.show()# 可视化每一列包含的节点
left_nodes=[0,1,2]
middle_nodes=[3,4]
right_nodes=[5,6]# 可视化时每个节点的坐标
pos = {n:(0,i) for i ,n in enumerate(left_nodes)}
pos.update({n:(1,i+0.5)for i,n in enumerate(middle_nodes)})
pos.update({n:(2,i+0.5)for i,n in enumerate(right_nodes)})print(pos)nx.draw_networkx(G,pos,**options)ax=plt.gca()
ax.margins(0.20) # 在图的边缘留白,防止节点被截断
plt.axis("off")
plt.show()
2.4.7 绘制房子图(例子)
# 尝试绘制房子图
G = nx.Graph([(0,1),(0,2),(1,3),(2,3),(2,4),(3,4)])pos = {0:(0,0),1:(1,0),2:(0,1),3:(1,1),4:(0.5,2.0)}plt.figure(figsize=(10,8))
nx.draw_networkx_nodes(G,pos,node_size=3000,nodelist=[0,1,2,3],node_color="#66ccff")
nx.draw_networkx_nodes(G,pos,node_size=3000,nodelist=[4],node_color="tab:orange")
nx.draw_networkx_edges(G,pos,alpha=0.5,width=6)
plt.axis("off") # 关闭坐标轴
plt.show()
2.4.8 可视化模板(重要)
# 一、基础可视化
# 创建有向图
seed=114514
G=nx.random_k_out_graph(10,3,0.5,seed=seed)
pos=nx.spring_layout(G,seed=seed)# 初步可视化
nx.draw(G,pos=pos,with_labels=True)
plt.show()# 二、高级可视化
# 节点大小
node_sizes = [12+10*i for i in range(len(G))]
print(node_sizes)# 节点颜色
M = G.number_of_edges()
edge_colors = range(2,M+2)
print(edge_colors)# 节点透明度
edge_alphas = [(5+i)/(M+4)for i in range(M)]
print(edge_alphas)# 配色方案
cmap = plt.get_cmap('plasma')
# cmap = plt.cm.Bluesplt.figure(figsize=(10,8))# 绘制节点
nodes = nx.draw_networkx_nodes(G,pos,node_size=node_sizes,node_color="indigo")# 绘制链接edges = nx.draw_networkx_edges(G,pos,node_size=node_sizes, # 节点尺寸arrowstyle="->", # 箭头样式arrowsize=20, # 箭头尺寸edge_color=edge_colors, # 连接颜色edge_cmap=cmap, # 连接配色方案width=4 # 连接线宽
)# 设置每个连接的透明度
for i in range(M):edges[i].set_alpha(edge_alphas[i])# 调色图例
pc = mpl.collections.PathCollection(edges,cmap=cmap)
pc.set_array(edge_colors)
plt.colorbar(pc)ax=plt.gca()
ax.set_axis_off()
plt.show()
2.4.9 自我中心图(ego图)
Ego graph指距离中心节点小于特定距离(特定路径长度)的所有结点构成的图,特定距离通常为1,即与中心节点直接有边连接。例如,假设下图左为一个完整的图,图右为以DDD为中心节点的ego-graph。换句话说,所谓的ego network,它的节点是由唯一的一个中心节点(ego),以及这个节点的邻居(alters)组成的,它的边只包括了ego和alter之间,以及alter与alter之间的边。
有的也称为Ego Network。
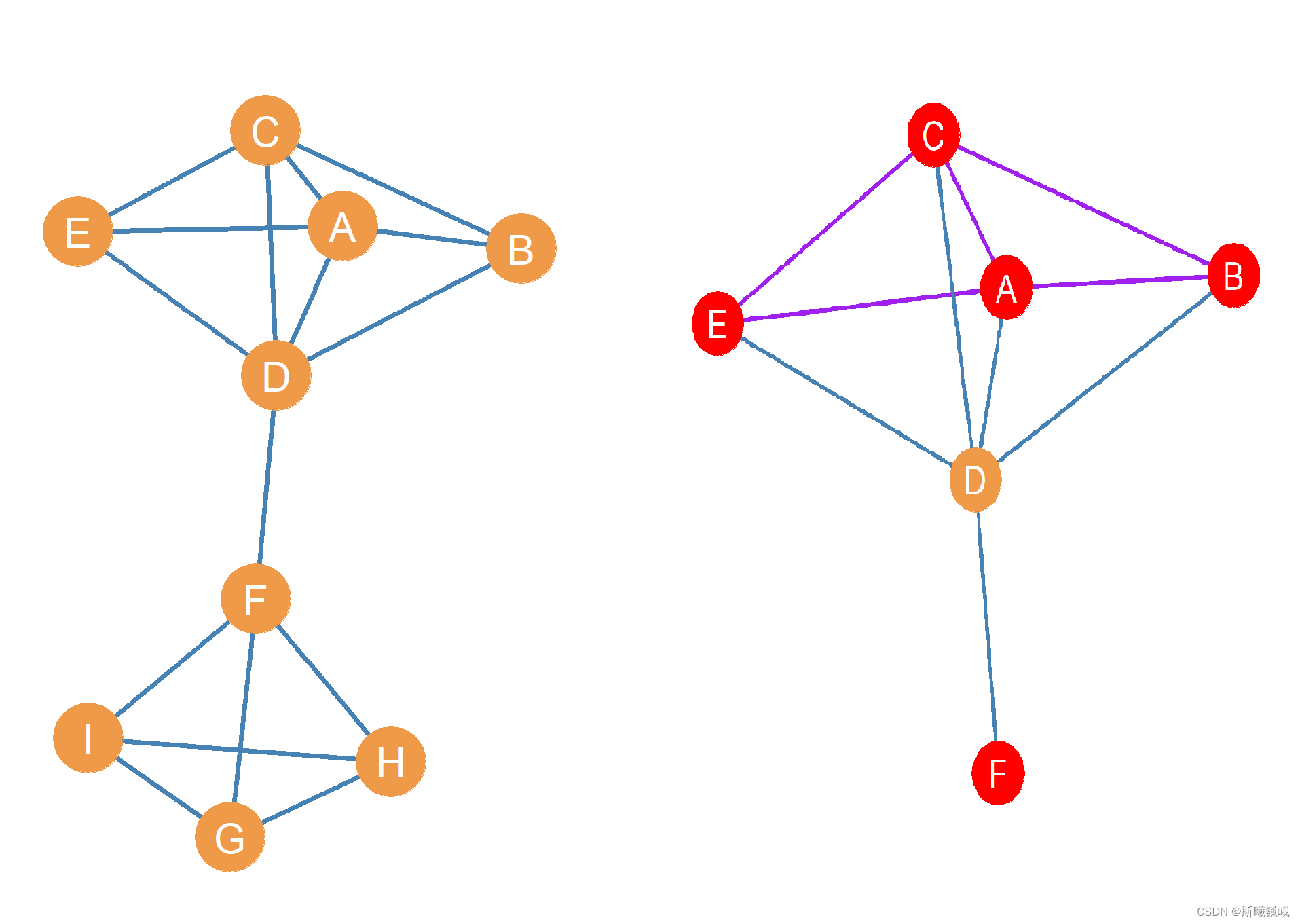
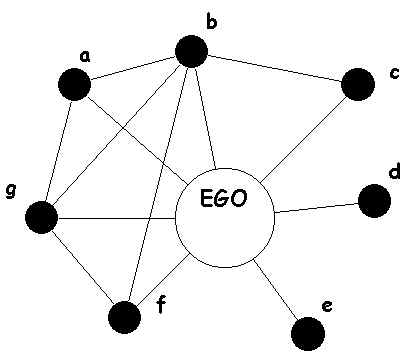
其中,图里面的每个alter和它自身的邻居又可以构成一个ego network,而所有节点的ego network合并起来,就可以组成真实的social network了。
Ego graph中的中心被称为ego(DDD),而其它与ego连接的节点被称为alter(A,B,C,E,FA,B,C,E,FA,B,C,E,F)。
在ego图中,除了ego与alter之间有边外,例如{DA,DB,DC,DE,DF}\{DA, DB,DC,DE,DF\}{DA,DB,DC,DE,DF},alter和alter之间也可以存在边(可选的,可能存在也可能不存在),例如{AC,AB,AE,BC,CE}\{AC,AB,AE,BC,CE\}{AC,AB,AE,BC,CE}。
跟ego graph有关联的有一个称之为N-step neighborhood的概念,它指的是与同ego间路径长度为NNN的所有“邻居”。
2.5 图相关数据分析
2.5.1 计算PageRank节点重要度
G =nx.star_graph(7)
nx.draw(G,with_labels=True)# 计算PageRank节点重要度PageRank = nx.pagerank(G,alpha=0.8)
print(PageRank)
2.5.2 最大连通域子图
# 一、创建图
# 创建 Erdos-Renyi 随机图,也称作 binomial graph
# n-节点数
# p-任意两个节点产生连接的概率G = nx.gnp_random_graph(100,0.02,seed=10374196)# 初步可视化
pos = nx.spring_layout(G,seed=10)
nx.draw(G,pos)
plt.show()
# 二、最大连通阈子图
Gcc = G.subgraph(sorted(nx.connected_components(G),key=len,reverse=True)[0])pos=nx.spring_layout(Gcc,seed=1039653)nx.draw_networkx_nodes(Gcc,pos,node_size=20)
nx.draw_networkx_edges(Gcc,pos,alpha=0.4)
plt.show()
2.5.3 每个节点的连接数(degree)
G = nx.gnp_random_graph(100,0.02,seed=10374196)# 排序一下
degree_sequence = sorted((d for n, d in G.degree()), reverse=True)
print(degree_sequence)
2.5.4 一些可能用到的图的基础数据
导入图
# 第一个参数指定头部节点数,第二个参数指定尾部节点数
G = nx.lollipop_graph(4, 7)# 可视化
pos = nx.spring_layout(G, seed=3068)
nx.draw(G, pos=pos, with_labels=True)
plt.show()# 图数据分析
# 半径
print(nx.radius(G))
# 直径
print(nx.diameter(G))
# 偏心度:每个节点到图中其它节点的最远距离
print(nx.eccentricity(G))
# 中心节点,偏心度与半径相等的节点
print(nx.center(G))
# 外围节点,偏心度与直径相等的节点
print(nx.periphery(G))print(nx.density(G))# 3号节点到图中其它节点的最短距离
node_id = 3
nx.single_source_shortest_path_length(G, node_id)# 每两个节点之间的最短距离
pathlengths = []
for v in G.nodes():spl = nx.single_source_shortest_path_length(G, v)for p in spl:print('{} --> {} 最短距离 {}'.format(v, p, spl[p]))pathlengths.append(spl[p])# 平均最短距离
print(sum(pathlengths) / len(pathlengths))# 不同距离的节点对个数
dist = {}
for p in pathlengths:if p in dist:dist[p] += 1else:dist[p] = 1
print(dist)
2.5.5 节点特征(重要)
# 可视化辅助函数
def draw(G, pos, measures, measure_name):nodes = nx.draw_networkx_nodes(G, pos, node_size=250, cmap=plt.cm.get_cmap('plasma'),node_color=list(measures.values()),nodelist=measures.keys())nodes.set_norm(mcolors.SymLogNorm(linthresh=0.01, linscale=1))# labels = nx.draw_networkx_labels(G, pos)edges = nx.draw_networkx_edges(G, pos)# plt.figure(figsize=(10,8))plt.title(measure_name)plt.colorbar(nodes)plt.axis('off')plt.show()# 导入无向图
G = nx.karate_club_graph()
pos = nx.spring_layout(G, seed=675)
nx.draw(G, pos, with_labels=True)
plt.show()# 导入有向图
DiG = nx.DiGraph()
DiG.add_edges_from([(2, 3), (3, 2), (4, 1), (4, 2), (5, 2), (5, 4),(5, 6), (6, 2), (6, 5), (7, 2), (7, 5), (8, 2),(8, 5), (9, 2), (9, 5), (10, 5), (11, 5)])
# dpos = {1: [0.1, 0.9], 2: [0.4, 0.8], 3: [0.8, 0.9], 4: [0.15, 0.55],
# 5: [0.5, 0.5], 6: [0.8, 0.5], 7: [0.22, 0.3], 8: [0.30, 0.27],
# 9: [0.38, 0.24], 10: [0.7, 0.3], 11: [0.75, 0.35]}
nx.draw(DiG, pos, with_labels=True)
plt.show()# Node Degree
print(list(nx.degree(G)))
print(dict(G.degree()))
# 字典按值排序
print(sorted(dict(G.degree()).items(), key=lambda x: x[1], reverse=True))
draw(G, pos, dict(G.degree()), 'Node Degree')# 节点重要度特征(节点的度,相当于将节点数归一化后的结果) Centrality
# Degree Centrality-无向图
print(nx.degree_centrality(G))
draw(G, pos, nx.degree_centrality(G), 'Degree Centrality')# Degree Centrality-有向图
print(nx.in_degree_centrality(DiG))
print(nx.out_degree_centrality(DiG))
draw(DiG, pos, nx.in_degree_centrality(DiG), 'DiGraph Degree Centrality')draw(DiG, pos, nx.out_degree_centrality(DiG), 'DiGraph Degree Centrality')# Eigenvector Centrality-无向图(特征向量重要度)
print(nx.eigenvector_centrality(G))
draw(G, pos, nx.eigenvector_centrality(G), 'Eigenvector Centrality')# Eigenvector Centrality-有向图(特征向量重要度)
print(nx.eigenvector_centrality_numpy(DiG))
draw(DiG, pos, nx.eigenvector_centrality_numpy(DiG), 'DiGraph Eigenvector Centrality')# Betweenness Centrality(必经之地)
print(nx.betweenness_centrality(G))
draw(G, pos, nx.betweenness_centrality(G), 'Betweenness Centrality')# Closeness Centrality(去哪儿都近)
print(nx.closeness_centrality(G))
draw(G, pos, nx.closeness_centrality(G), 'Closeness Centrality')# PageRank
print(nx.pagerank(DiG, alpha=0.85))
draw(DiG, pos, nx.pagerank(DiG, alpha=0.85), 'DiGraph PageRank')# Katz Centrality
print(nx.katz_centrality(G, alpha=0.1, beta=1.0))
draw(G, pos, nx.katz_centrality(G, alpha=0.1, beta=1.0), 'Katz Centrality')
draw(DiG, pos, nx.katz_centrality(DiG, alpha=0.1, beta=1.0), 'DiGraph Katz Centrality')# HITS Hubs and Authorities
h, a = nx.hits(DiG)
draw(DiG, pos, h, 'DiGraph HITS Hubs')
draw(DiG, pos, a, 'DiGraph HITS Authorities')# NetworkX文档:社群属性 Clustering
print(nx.draw(G, pos, with_labels=True))# 三角形个数
print(nx.triangles(G))
print(nx.triangles(G, 0))
draw(G, pos, nx.triangles(G), 'Triangles')# Clustering Coefficient
print(nx.clustering(G))
print(nx.clustering(G, 0))
draw(G, pos, nx.clustering(G), 'Clustering Coefficient')# Bridges
# 如果某个连接断掉,会使连通域个数增加,则该连接是bridge。
# bridge连接不属于环的一部分。
pos = nx.spring_layout(G, seed=675)
nx.draw(G, pos, with_labels=True)
plt.show()
print(list(nx.bridges(G)))# Common Neighbors 和 Jaccard Coefficient
pos = nx.spring_layout(G, seed=675)
nx.draw(G, pos, with_labels=True)
plt.show()
print(sorted(nx.common_neighbors(G, 0, 4)))
preds = nx.jaccard_coefficient(G, [(0, 1), (2, 3)])
for u, v, p in preds:print(f"({u}, {v}) -> {p:.8f}")
for u, v, p in nx.adamic_adar_index(G, [(0, 1), (2, 3)]):print(f"({u}, {v}) -> {p:.8f}")# Katz Index
# 节点u到节点v,路径为k的路径个数。
import numpy as np
from numpy.linalg import invG = nx.karate_club_graph()
print(len(G.nodes))
# 计算主特征向量
L = nx.normalized_laplacian_matrix(G)
e = np.linalg.eigvals(L.A)
print('最大特征值', max(e))# 折减系数
beta = 1 / max(e)# 创建单位矩阵
I = np.identity(len(G.nodes))# 计算 Katz Index
S = inv(I - nx.to_numpy_array(G) * beta) - I
print(S.shape)
print(S.shape)
2.5.6 计算全图的Graphlet
# 导入全图
G = nx.karate_club_graph()plt.figure(figsize=(10,8))
pos = nx.spring_layout(G, seed=123)
nx.draw(G, pos, with_labels=True)# 指定Graphlet
target = nx.complete_graph(3)
nx.draw(target)
plt.show()# 匹配Graphlet,统计个数
num = 0
for sub_nodes in itertools.combinations(G.nodes(), len(target.nodes())): # 遍历全图中,符合graphlet节点个数的所有节点组合subg = G.subgraph(sub_nodes) # 从全图中抽取出子图if nx.is_connected(subg) and nx.is_isomorphic(subg, target): # 如果子图是完整连通域,并且符合graphlet特征,输出原图节点编号num += 1print(subg.edges())print(num)
2.6.7 拉普拉斯矩阵特征值分解
import numpy.linalg # 线性代数# 创建图
n = 1000 # 节点个数
m = 5000 # 连接个数
G = nx.gnm_random_graph(n, m, seed=5040)# 邻接矩阵(Adjacency Matrix)
A = nx.adjacency_matrix(G)
print(A.shape)
print(A.todense())# 拉普拉斯矩阵(Laplacian Matrix)
L = nx.laplacian_matrix(G)
print(L.shape)# 节点degree对角矩阵
D = L + A
print(D.todense())# 归一化拉普拉斯矩阵(Normalized Laplacian Matrix)
L_n = nx.normalized_laplacian_matrix(G)
print(L_n.shape)
print(L_n.todense())
plt.imshow(L_n.todense())
plt.show()
print(type(L_n))# 特征值分解
e = np.linalg.eigvals(L_n.A)
print(e)
# 最大特征值
print(max(e))
# 最小特征值
print(min(e))# 特征值分布直方图
plt.figure(figsize=(12, 8))plt.hist(e, bins=100)
plt.xlim(0, 2) # eigenvalues between 0 and 2plt.title('Eigenvalue Histogram', fontsize=20)
plt.ylabel('Frequency', fontsize=25)
plt.xlabel('Eigenvalue', fontsize=25)
plt.tick_params(labelsize=20) # 设置坐标文字大小
plt.show()
参考文献
[1] NetworkX 图网络处理工具包
[2] python 工具包 NetworkX 教程翻译
[3] Ego Graph概念介绍
[4] ego network的概念
相关文章:

[Datawhale][CS224W]图机器学习(三)
目录一、简介与准备二、教程2.1 下载安装2.2 创建图2.2.1 常用图创建(自定义图创建)1.创建图对象2.添加图节点3.创建连接2.2.2 经典图结构1.全连接无向图2.全连接有向图3.环状图4.梯状图5.线性串珠图6.星状图7.轮辐图8.二项树2.2.3 栅格图1.二维矩形栅格…...

2023版最新最强大数据面试宝典
此套面试题来自于各大厂的真实面试题及常问的知识点,如果能理解吃透这些问题,你的大数据能力将会大大提升,进入大厂指日可待!目前已经更新到第4版,广受好评!复习大数据面试题,看这一套就够了&am…...

CSS 中的 BFC 是什么,有什么作用?
BFC,即“块级格式化上下文”(Block Formatting Context),是 CSS 中一个重要的概念,它指的是一个独立的渲染区域,让块级盒子在布局时遵循一些特定的规则。BFC 的存在使得我们可以更好地控制文档流࿰…...

总结在使用 Git 踩过的坑
问题一: 原因 git 有两种拉代码的方式,一个是 HTTP,另一个是 ssh。git 的 HTTP 底层是通过 curl 的。HTTP 底层基于 TCP,而 TCP 协议的实现是有缓冲区的。 所以这个报错大致意思就是说,连接已经关闭,但是此时有未处理…...

从 HTTP 到 gRPC:APISIX 中 etcd 操作的迁移之路
罗泽轩,API7.ai 技术专家/技术工程师,Apache APISIX PMC 成员。 原文链接 Apache APISIX 现有基于 HTTP 的 etcd 操作的局限性 etcd 在 2.x 版本的时候,对外暴露的是 HTTP 1 (以下简称 HTTP)的接口。etcd 升级到 3.x…...
【C语言每日一题】——倒置字符串
【C语言每日一题】——倒置字符串😎前言🙌倒置字符串🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神贯注的上吧!!! 😊作者简…...

Native扩展开发的一般流程(类似开发一个插件)
文章目录大致开发流程1、编写对应的java类服务2、将jar包放到对应位置3、配置文件中进行服务配置4、在代码中调用5、如何查看服务调用成功大致开发流程 1、编写服务,打包为jar包2、将jar包放到指定的位置3、在配置文件中进行配置,调用对应的服务 1、编…...

【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 任务调度 题目 现有一个 CPU 和一些任务需要处理,已提前获知每个任务的任务 ID、优先级、所需执行时间和到达时间。 CPU 同时只能运行一个任务,请编写一个任务调度程序,采用“可抢占优先权调度”调度…...
Spring3定时任务
简介 Spring 内部有一个 task 是 Spring 自带的一个设定时间自动任务调度,提供了两种方式进行配置,一种是注解的方式,而另外一种就是 XML 配置方式了;注解方式比较简洁,XML 配置方式相对而言有些繁琐,但是应用场景的不…...
数据库版本管理工具Flyway应用研究
目录1 为什么使用数据库版本控制2 数据库版本管理工具选型:Flyway、Liquibase、Bytebase、阿里 DMSFlywayLiquibaseBytebase阿里 DMS3 Flyway数据库版本管理研究3.1 参考资料3.2 Flyway概述3.3 Flyway原理3.4 Flyway版本和功能3.5 Flyway概念3.5.1 版本迁移…...

更换 Ubuntu 系统 apt 命令安装软件源
更换 Ubuntu 系统 apt 命令安装软件源清华大学开源软件镜像站 https://mirrors.tuna.tsinghua.edu.cn/ 1. Ubuntu 的软件源配置文件 /etc/apt/sources.list MIRRORS -> 使用帮助 -> ubuntu https://mirrors.tuna.tsinghua.edu.cn/help/ubuntu/ Ubuntu 系统 apt 命令安…...
2023年可见光通信(LiFi)研究新进展
可见光无线通信Light Fidelity(LiFi)又称“光保真技术”,是一种利用可见光进行数据传输的全新无线传输技术。LiFi是一种以半导体光源作为信号发射源,利用无需授权的自由光谱实现无线连接的新型无线通信技术,支持高密度…...
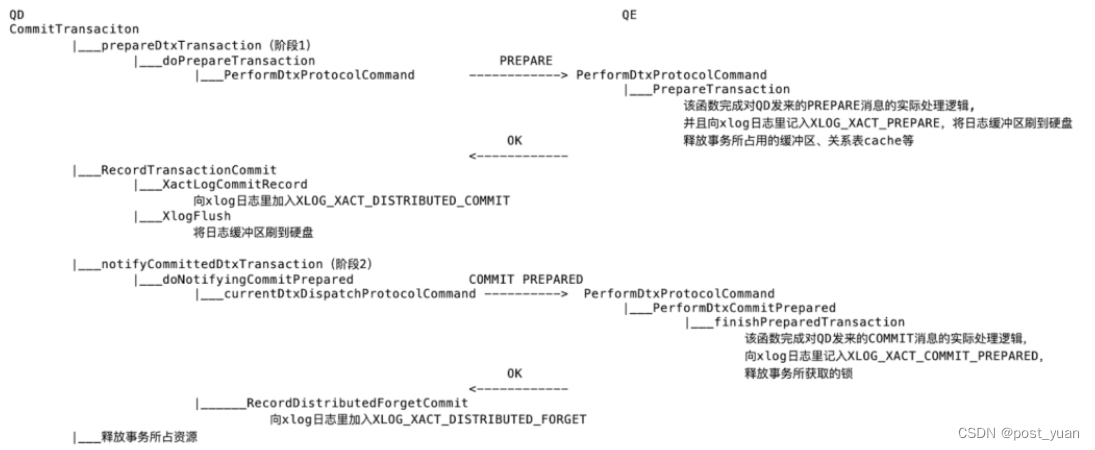
Greenplum的两阶段提交
注:本文章引自终于把分布式事务讲明白了! 在前面的文章中,我们了解了单机库中的事务一致性实现以及分布式事务中的两阶段提交协议。大多数分布式系统都是采用了两阶段提交塄来保证事务的原子性,Greenplum也是采用了两阶段提交&am…...
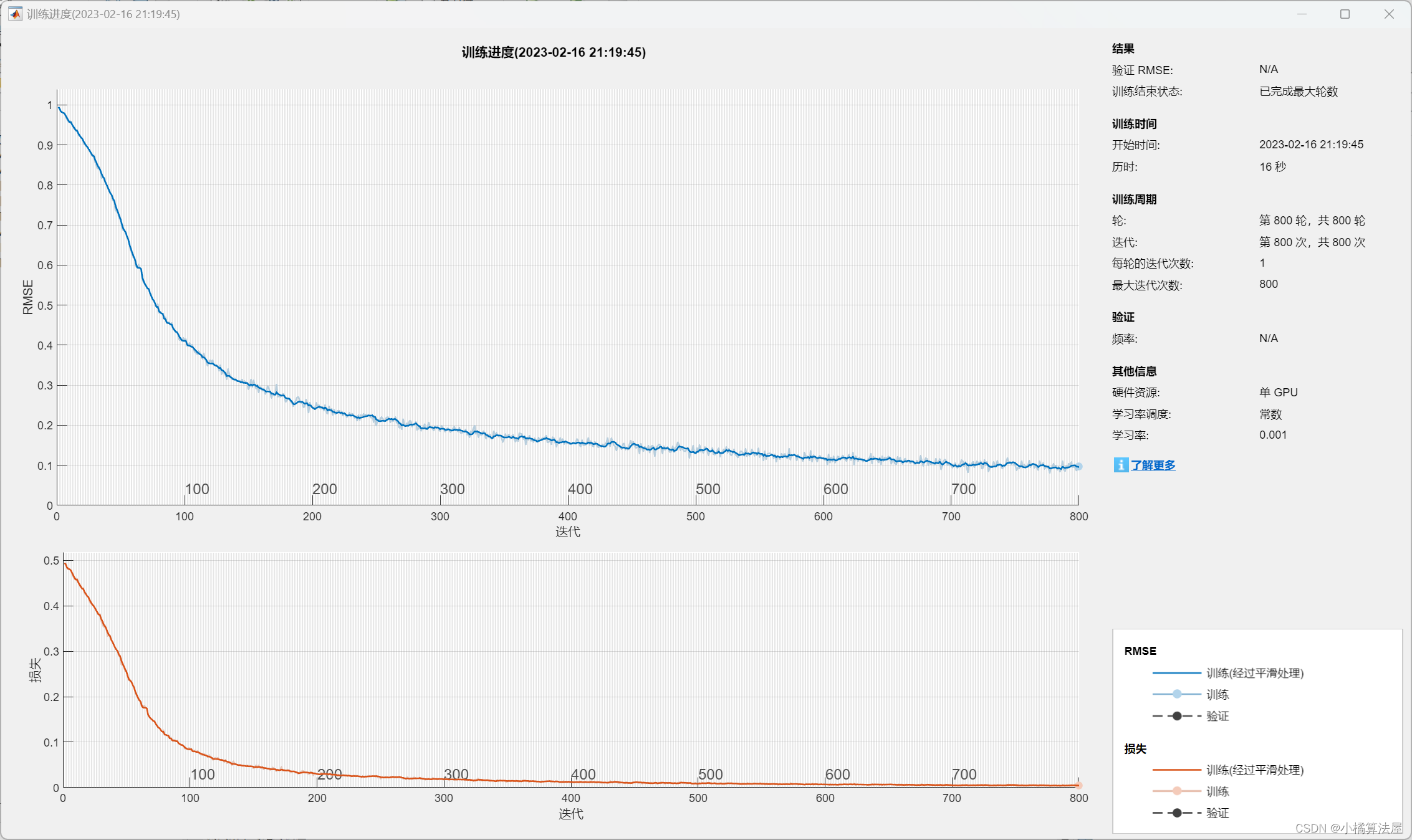
多元回归分析 | CNN-BiLSTM卷积双向长短期记忆神经网络多输入单输出预测(Matlab完整程序)
多元回归分析 | CNN-BiLSTM卷积双向长短期记忆神经网络多输入单输出预测(Matlab完整程序) 目录 多元回归分析 | CNN-BiLSTM卷积双向长短期记忆神经网络多输入单输出预测(Matlab完整程序)预测结果评价指标基本介绍程序设计参考资料预测结果 评价指标 训练结束: 已完成最大轮…...
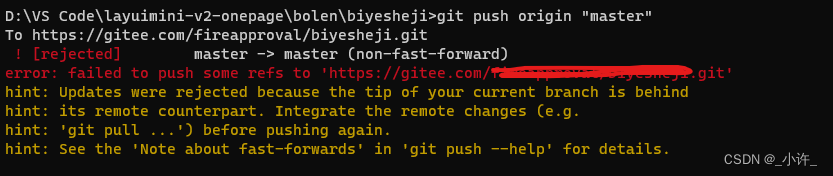
git命令行推送本地分支到远程仓库
之前说过Git与IDEA强强联合(HTTPS协议连接)那么如何使用命令行来推送代码呢? 如下图所示为一个基于layui的前端代码: 目录工作区文件: 本地内容就是将这些内容推送到远程仓库 首先使用git命令初始化git本地仓库&…...
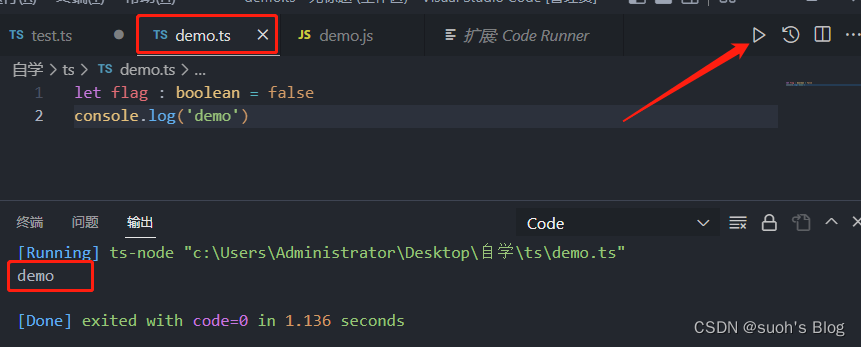
在vscode中使用Typescript并运行
首先呢,我们在学习ts之前,需要先安装ts 1、安装 typescript npm install -g typescript //检查是否安装tsc -v 2、生成配置文件,cd进入该文件夹,在控制台输 tsc --init 此时我们就可以看到在ts文件夹下面出现了 一个tsco…...
)
【C++提高编程】C++全栈体系(十九)
C提高编程 第三章 STL - 常用容器 一、string容器 1. string基本概念 本质: string是C风格的字符串,而string本质上是一个类 string和char * 区别: char * 是一个指针string是一个类,类内部封装了char*,管理这个…...
、Modbus串口虚拟工具、网络串口调试工具分享)
Java版电能表协议解析源码(DL/T645-2007)、Modbus串口虚拟工具、网络串口调试工具分享
什么是Modbus通信协议Modbus串口调试工具Java版协议解析源码 网络与串口二合一调试助手TCPCOM: https://download.csdn.net/download/liuyuan_java/87454762 Modbus调试工具,模拟串口调试工具 https://download.csdn.net/download/liuyuan_java/874274…...

2023美赛选题建议 美国大学生数学建模竞赛ABCDEF题
选题建议和粗略思路已更新完毕 对于没有基础的同学来说CD两题上手难度较高,大家可以根据自己的实际情况选择最适合自己的题目,团队将持续更新各题后续内容,Q群322297051 A题主要难度就是建立第一问的模型,综合来看难度不大&…...

2023,想跳槽的可以再等等
今天讲讲跳槽。 金三银四即将开启,一些不满现状,被外界的“高薪”“好福利”吸引的人,一般就在这时候毅然决然地跳槽了。 跳槽是为了寻求更好的发展,但在跳槽前我们也不能确定下家就是更好的归宿,这就更加需要我们审…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
