空间复杂度与时间复杂度
1、时间复杂度和空间复杂度
(1)时间复杂度、空间复杂度是什么?
- 算法效率分析分为两种:第一种是时间效率,第二种是空间效率。
- 时间效率被称为时间复杂度,空间效率被称作空间复杂度
- 时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间
- 在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度,如今更加考虑时间复杂度
(2)时间复杂度的计算
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}//实际执行N * N + 2 * N + 10
①代码解析
实际的们计算时间复杂度的时候,不用计算如此精确的执行次数,于是这里我们使用大O渐进表示法,时间复杂度不算时间,算次数
②大O表示法
是用于描述函数渐进行为的数学符号
③推导方法
- 用常数1取代运行时间中的所有加法常数
- 在修改后的运行函数中,只保留最高阶项
- 如果高阶项存在且不是1,则去除于这个项目相乘的常数
④最好、平均、最坏情况:
- 最好情况:任意输入规模的最大运行次数(上界)
- 平均情况:任意输入规模的期望运行次数
- 最好情况:任意输入规模的最小运行次数(下界)
⑤推导例子
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
//2 * N + 10 ====> O(N)
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count; }printf("%d\n", count);
}
//M + N====>O(M + N)
//如果M远大于N====>O(M)
//如果M、N相差不大====>O(2 * M)/O(2 * N)====>O(M)/O(N)
void Func4(int N)//N没有用到,时间复杂度与N无关
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
//100====>O(1),反过来就说明输入数据了常数次
//计算strchr的时间复杂度?
const char * strchr ( const char * str, char character )
{while(*str != '\0'){if(*str == character)return str;++str;}return NULL;
}
//需要分情况:最坏、平均、最好,假设字符串长度为N
//最坏的没有找到或者在最后找到====>O(N)
//平均就是O(N / 2)
//最坏就是O(1)
//当要分情况的时候要用最坏的情况表示,因此最终结果就是O(N)
// 计算BubbleSort的时间复杂度?(冒泡排序)
void BubbleSort(int* a, int n)
{assert(a);//断言for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);//调换两个元素exchange = 1;}}if (exchange == 0)break;}
}
//这个也要分情况
//第一次冒泡N次(也可以理解为N - 1的)
//第二次冒泡N - 1次
//……
//第N次冒泡1次
//和为((1 + N) * N) / 2
//因此最坏情况O(N^2)
// 计算BinarySearch的时间复杂度?(二分查找法)
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n;while (begin < end){int mid = begin + ((end-begin) >> 1);//求平均值if (a[mid] < x){ begin = mid+1;}else if (a[mid] > x){end = mid;}else{return mid;}}return -1;
}
//这个也要分情况
//O(log(2)N)简写为log(N),最好不要写lg(N)尽管有的地方会这样写,详细解说在下面

// 计算阶乘递归Factorial的时间复杂度?
long long Factorial(size_t N)
{return N < 2 ? N : Factorial(N-1) * N;
}
//Factorial(10)
//Factorial(9) * 10
//Factorial(8) * 9
//……
//Factorial(1) * 2
递归了N次,每次就是O(1),整体就是O(N)
//如果假设递归内用的是循环语句for(int i = 0; i < N; ++i);则每次是O(N),整体就是O(N^2)
⑥常见的时间复杂度对比
O(1) < O(logN) < O(N) < O(N^2)
(3)空间复杂度的计算
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
//标粗的地方占用了变量,即5====>O(1)
//注意时间是累积的,空间是不累积的(因为重复利用了一个空间)
①代码解析
实际的们计算空间复杂度的时候,也不用计算如此精确的空间,只需要知道大概的执行次数即可,于是这里我们也同样使用大O渐进表示法,空间复杂度不算空间,算变量个数
②大O表示法
是用于描述函数渐进行为的数学符号
③推导方法
- 用常数1取代运行时间中的所有加法常数
- 在修改后的运行函数中,只保留最高阶项
- 如果高阶项存在且不是1,则去除于这个项目相乘的常数
④推导例子
// 计算Fibonacci的空间复杂度?(斐波那契数列)
long long* Fibonacci(size_t n)
{if(n==0){return NULL;}long long* fibArray = (long long*)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}
//O(N + 6)====>O(N)
//虽然大部分算法的空间复杂度都是O(1)
// 计算阶乘递归Factorial的空间复杂度?
long long Factorial(size_t N)
{return N < 2 ? N : Factorial(N - 1) * N;
}
//递归调用了n层,每次调用建立一个栈帧,每次使用了常数O(1),整体就是O(N)
2、有关的练习题目
(1)面试题 17.04. 消失的数字 - 力扣(LeetCode)
//思路一:
int missingNumber(int* nums, int numsSize)
{int add_1 = 0;int add_2 = 0;add_1 = ( (0 + numsSize) * (numsSize + 1) ) / 2;for(int i = 0; i < numsSize; i++){add_2 += nums[i];}return add_1 - add_2;
}
//思路二:
int missingNumber(int* nums, int numsSize)
{int x = 0;int i = 0;for(i = 0; i < numsSize; i++)//用for循环求出数组nums元素的异或和{x ^= nums[i];}for(i = 0; i < numsSize + 1; i++)//运用异或的性质a^a=0来找出消失的数字{x ^= i;}return x;
}
(2)189. 轮转数组 - 力扣(LeetCode)
//思路一:
void rotate(int* nums, int numsSize, int k)
{while(k--){int tmp = nums[numsSize - 1];//保留最后一个数字for(int end = numsSize - 2; end >= 0; --end)//开始将最后一个数字前面的所有数字后移{nums[end + 1] = nums[end];}nums[0] = tmp;}
}
//但是超出了时间限制
//思路二:
void Reverse(int* nums, int left, int right)
{while(left < right)//奇数个会相等,偶数个会错开{int tmp = nums[left];nums[left] = nums[right];nums[right] = tmp;++left;--right;}
}
void rotate(int* nums, int numsSize, int k)
{if(k >= numsSize)//防止k大于数组大小,例如7个元素旋转13次和6次等价{k %= numsSize;}Reverse(nums, numsSize - k, numsSize - 1);//后半部分Reverse(nums, 0, numsSize - k - 1);//前半部分Reverse(nums, 0, numsSize - 1);
}
相关文章:

空间复杂度与时间复杂度
1、时间复杂度和空间复杂度 (1)时间复杂度、空间复杂度是什么? 算法效率分析分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,空间效率被称作空间复杂度时间复杂度主要衡量的是一…...

javaEE 初阶 — 延迟应答与捎带应答
文章目录1. 延迟应答2. 捎带应答TCP 工作机制:确认应答机制 超时重传机制 连接管理机制 滑动窗口 流量控制与拥塞控制 1. 延迟应答 延时应答 也是提升效率的机制,也是在滑动窗口基础上搞点事情。 滑动窗口的关键是让窗口大小大一点,传输…...

Twitter账号老被封?一文教会你怎么养号
昨天龙哥给大家科普完要怎么批量注册Twitter账号,立刻有朋友来私信龙哥说里面提到的这个养号和防关联具体是个怎么样的做法。由于Twitter检测机制还是比较敏感的,账号很容易被冻结,所以养号是非常重要的步骤。其实要养好Twitter账号其实并不难…...

当遇到国外客户的问题,你解决不了的时候怎么办
对我来说,今年的这个春节假期有点长,差不多休了一个月。复工之后,截止目前做到了60万RMB的业绩,但是相较于往年,整体状态还是差了些。往年的春节,我都是随时待命的状态,整个春节天天坐于电脑前&…...
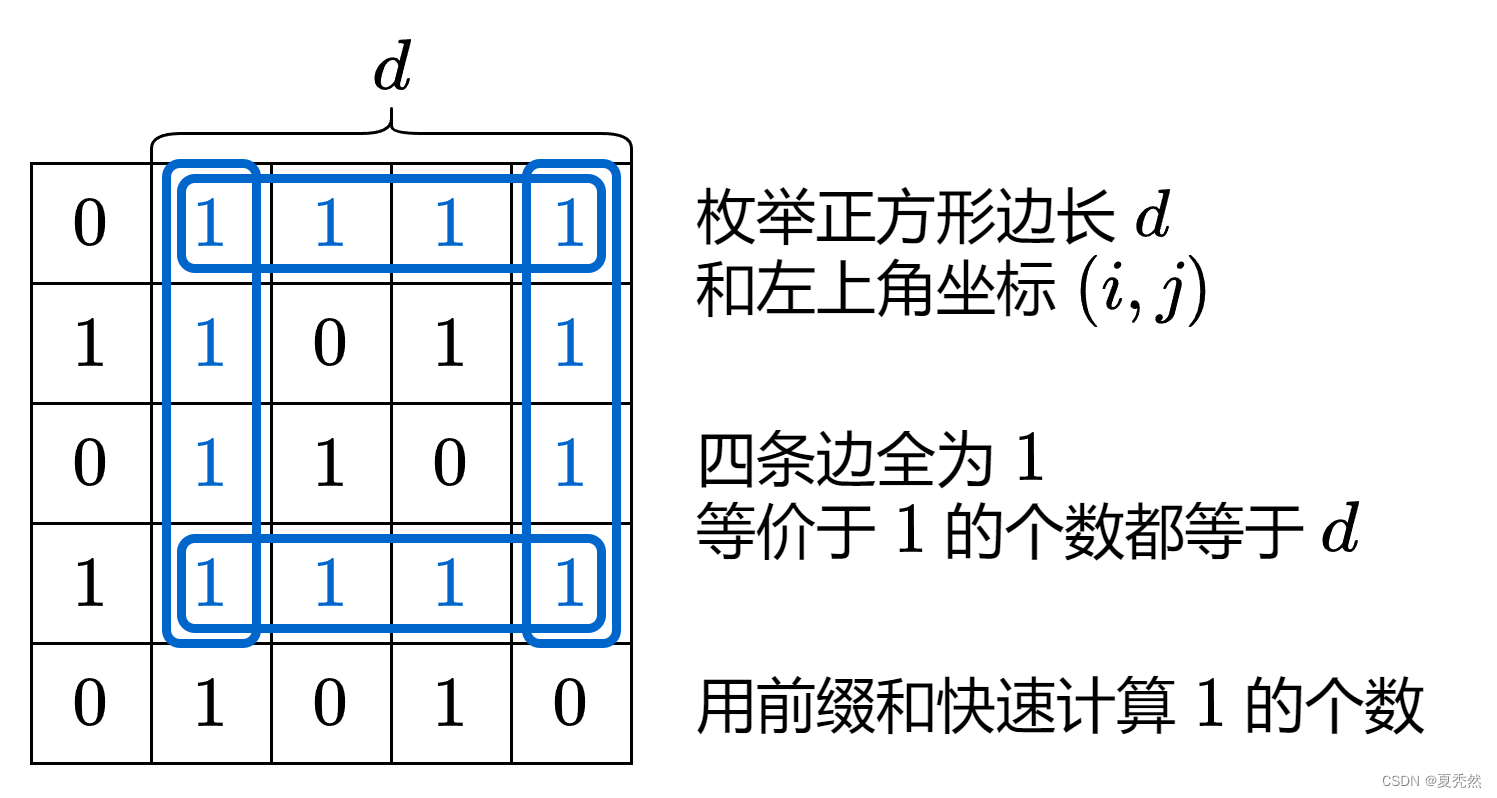
算法刷题打卡第93天: 最大的以 1 为边界的正方形
最大的以 1 为边界的正方形 难度:中等 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。 示例 1: 输入:…...
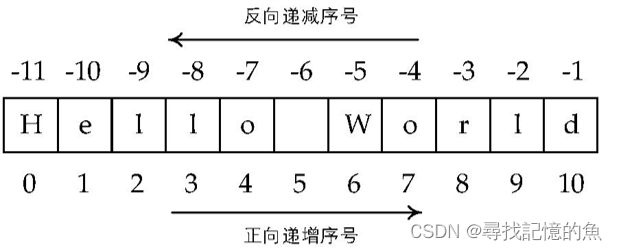
python语言基础(最详细版)
文章目录一、程序的格式框架缩进1、定义2、这里就简单的举几个例子注释二、语法元素的名称三、数据类型四、数值运算符五、关系运算六、逻辑运算七、运算符的结合性八、字符串一、程序的格式框架 缩进 1、定义 (1)python中通常用缩进来表示代码包含和…...

Java小技能:字符串
文章目录 引言I 预备知识1.1 Object类1.2 重写的规则1.3 hashCode方法II String2.1 String的特性2.2 字符串和正则2.3 StringBuilder,StringBuffer引言 String,StringBuffer,StringBuilder,char[],用来表示字符串。 I 预备知识 1.1 Object类 是所有类的根类 toString…...

2023美赛D题:可持续发展目标
以下内容全部来自人工翻译,仅供参考。 文章目录背景要求术语表文献服务背景 联合国制定了17个可持续发展目标(SDGs)。实现这些目标最终将改善世界上许多人的生活。这些目标并不相互独立,因此,一些目标的积极进展常常…...
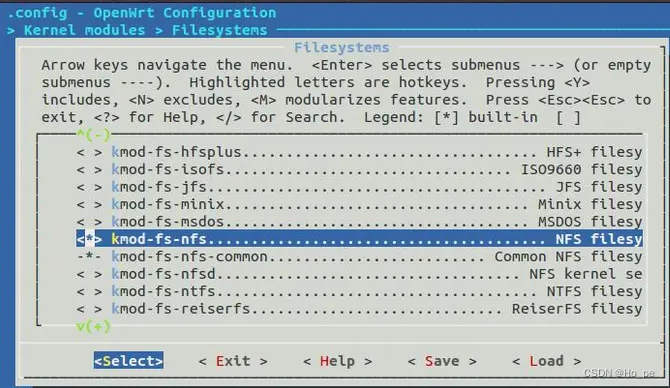
openwrt开发板与ubuntu nfs挂载
1.ubuntu需要安装nfs服务 sudo apt-get install nfs-common nfs-kernel-server2.修改 /etc/exports文件: /home/test *(rw,nohide,insecure,no_subtree_check,async,no_root_squash) 前面是挂载的目录,后边是相应权限 rw:读写 insecure&am…...

【Redis】Redis持久化之AOF详解(Redis专栏启动)
📫作者简介:小明java问道之路,2022年度博客之星全国TOP3,专注于后端、中间件、计算机底层、架构设计演进与稳定性建工设优化。文章内容兼具广度深度、大厂技术方案,对待技术喜欢推理加验证,就职于知名金融公…...

Git小乌龟每次推送拉取都弹窗和用户名密码报错(解决办法)
目录 一、小乌龟推送代码到云端用户名和密码报错 (一) 遇到问题 (二)解决办法 二、小乌龟每次推送拉取都要输入账号和密码 (一)遇到问题 (二)解决办法 一、小乌龟推送代码到云…...

emacs 使用集锦
emacs 使用集锦 声明, 主要在c/c环境中使用! ---------------------------------------- 1. emacs 中 TAGS 位置设置 ---------------------------------------- a)临时使用方式: M-x visit-tags-table b)启动Emacs时自动加载方式ÿ…...

蓝牙 - 如何实现安全性
蓝牙技术在加密上做了很多工作,来保证你的数据安全。 这些年来,我们的许多电子设备都转向了使用无线技术进行连接。我们的鼠标、键盘、耳机和扬声器上不再有长长的纠缠的电线,而使用了简单方便的无线技术,科技进步改善了我们的生活…...

深入理解顺序io和随机io(全网最详细篇)
MySql系列整体栏目 内容链接地址【一】深入理解mysql索引本质https://blog.csdn.net/zhenghuishengq/article/details/121027025【二】深入理解mysql索引优化以及explain关键字https://blog.csdn.net/zhenghuishengq/article/details/124552080【三】深入理解mysql的索引分类&a…...
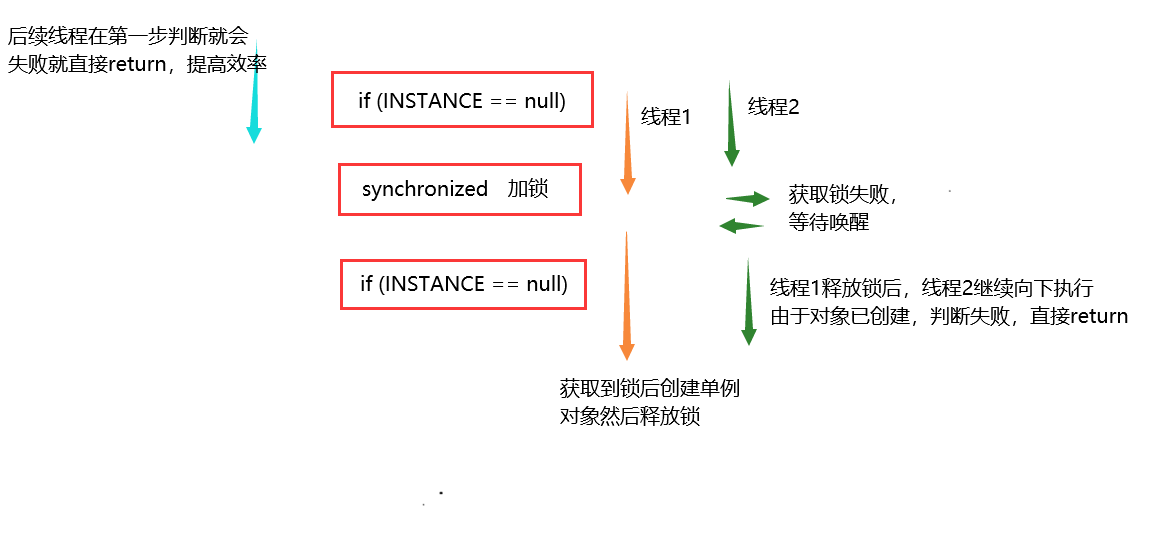
面试准备知识点与总结——(基础篇)
目录Java基础Java面向对象有哪些特征ArrayList和LinkedList有什么区别高并发的集合有哪些问题迭代器的fail-fast和fail-safeArrayList底层扩容机制HashMap面试合集解答设计模式单例设计模式哪些地方体现了单例模式Java基础 Java面向对象有哪些特征 Java面向对象有三大特征&am…...

Linux共享库,静态库与相关系统调用,工具的使用总结
tags: Linux C Syscall 写在前面 总结Unix/Linux操作系统的共享库/静态库部分, 以及一些系统调用. 参考Linux/UNIX系统编程手册41-42章. 测试程序均在Ubuntu下使用cc(gcc-9)运行成功. $ gcc -v Using built-in specs. COLLECT_GCCgcc COLLECT_LTO_WRAPPER/usr/lib/gcc/x86_64…...

「JVM 编译优化」javac 编译器源码解读
Java 的编译过程 前端编译: 编译器的前端,将 Java 文件转变成 Class 文件的过程;如 JDK 的 javac、Eclipse JDT 中的增量式编译器 ECJ;即使编译: JIT,Just In Time Compiler,在运行期将字节码转变成本地机器码的过程&…...

Leetcode DAY 34: K次取反后最大化的数组和 and 加油站 and 分发糖果
1005.K次取反后最大化的数组和 class Solution:def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:nums sorted(nums, key abs, reverse True)for i in range(len(nums)):if nums[i] < 0:nums[i] -nums[i]k - 1else:continueif k 0:return sum(…...

2023美赛A题思路
在线解析 https://kdocs.cn/l/ccNGjN9sGugLkdocs.cn/l/ccNGjN9sGugL A题思路:(具体以题目解决问题顺序为主) 这道题分析植被就行,主要涉及不同植被间的相互作用,有竞争有相互促进,我查了下“植物科学数…...

前端上传文件
前言 以 vue 举例,原生 html css js 现在应该很少有人去写了 一、绘制样式 绘制两个标签,一个 <div></div> ,一个 <input type"file" />; 为 <div></div>添加 css 样式,…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
