【王道数据结构】第七章| 查找 | 树
目录
一、查找
1、查找概念
2、顺序查找
3、折半查找
4、分块查找
二、树
1、B树
2、B树的基本操作
3、B+树
4、散列查找及其性能分析
5、散列查找及性能分析
一、查找
1、查找概念

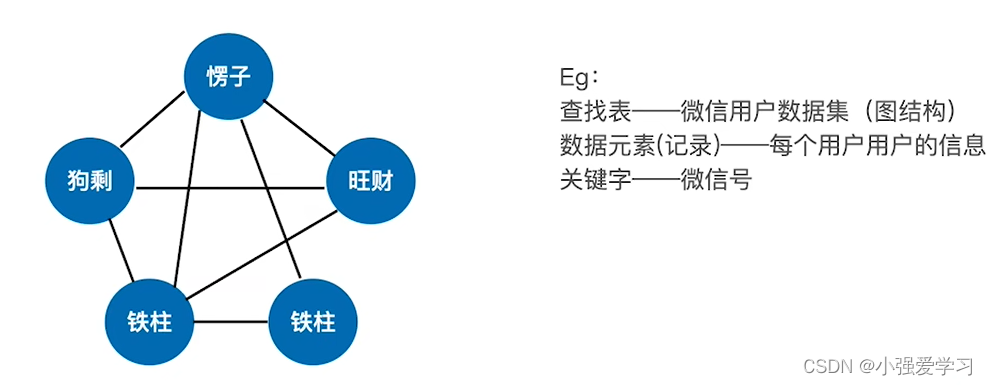
- 查找:在数据集合中寻找满足某种条件的数据元素的过程称为查找。
- 查找表(查找结构):用于查找的。数据集合称为查找表,它由同一类型的数据元素 (或记录)组成。
- 关键字:数据元素中唯一标识该元素的某个数据项的值,使用基于关键字的查找,查找结果应该是唯一的。
如下举例:
- 查找长度:在查找运算中,需要对比关键字的次数称为查找长度。
- 平均查找长度(ASL,Average Search Length): 所有查找过程中进行关键字的比较次数的平均值。
2、顺序查找
- 顺序查找,又叫“线性查找”,通常用于线性表算法
- 思想:从头到 jio 个找 (或者反过来也OK)
代码实现:
typedef struct{ //查找表的数据结构(顺序表)ElemType *elem; //动态数组基址int TableLen; //表的长度
}SSTable;//顺序查找
int Search_Seq(SSTable ST,ElemType key){int i;for(i=0;i<ST.TableLen && ST.elem[i]!=key;++i);// 查找成功返回数组下标,否则返回-1return i=ST.TableLen? -1 : i;
}
哨兵方式代码实现:
typedef struct{ //查找表的数据结构(顺序表)ElemType *elem; //动态数组基址int TableLen; //表的长度
}SSTable;//顺序查找
int Search_Seq(SSTable ST,ElemType key){ST.elem[0]=key;int i;for(i=ST.TableLen;ST.elem[i]!=key;--i)// 查找成功返回数组下标,否则返回0return i;
}
用查找判定树分析ASL
- 一个成功结点的查找长度=自身所在层数
- 一个失败结点的查找长度 =其父节点所在
- 层数默认情况下,各种失败情况或成功情况都等概率发生
3、折半查找

【折半查找概念】
- 折半查找,又称“二分查找”,仅适用于有序的顺序表
折半查找代码实现:
typedef struct{ElemType *elem;int TableLen;
}SSTable;// 折半查找
int Binary_Search(SSTable L,ElemType key){int low=0,high=L.TableLen,mid;while(low<=high){mid=(low+high)/2;if(L.elem[mid]==key)return mid;else if(L.elem[mid]>key)high=mid-1; //从前半部分继续查找elselow=mid+1; //从后半部分继续查找}return -1;
}
- 折半查找判定树的构造:m i d = ⌊ ( l o w + h i g h ) / 2 ⌋ ,如果当前 low 和 high 之间有奇数个元素,则 mid 分隔后,左右两部分元素个数相等;如果当前 low 和 high 之间有偶数个元素,则 mid 分隔后,左半部分⽐右半部分少⼀个元素。
- 折半查找的判定树中,若m i d = ⌊ ( l o w + h i g h ) / 2 ⌋ ,则对于任何⼀个结点,必有:右⼦树结点数 - 左⼦树结点数 = 0 或 1。
- 折半查找的判定树⼀定是平衡⼆叉树。折半查找的判定树中,只有最下⾯⼀层是不满的。因此,元素个数为 n 时树⾼ h = ⌈ l o g 2 ( n + 1 ) ⌉ 。
- 判定树结点关键字:左<中<右,满⾜⼆叉排序树的定义。失败结点:n+1个(等于成功结点的空链域数量)
- 折半查找的查找效率:折半查找的时间复杂度 = O ( l o g 2 n ) 。
4、分块查找
分块查找所针对的情况:块内⽆序、块间有序。

索引表及顺序表代码
// 索引表
typedef struct{ElemType maxValue;int low,high;
}Index;// 顺序表存储实际元素
ElemType List[100];
- 查找目标关键字所在分块可使用顺序查找和折半查找两种方式。
- 若使用折半查找且索引表中不包含⽬标关键字,则最终要停在 low > high,要在 low 所指分块中查找目标关键字。
- 查找效率分析(ASL):假设⻓度为 n 的查找表被均匀地分为 b 块,每块 s 个元素。设索引查找和块内查找的平均查找⻓度分别为 ASL=LI+LS
二、树
1、B树
B树,⼜称多路平衡查找树,B树中所有结点的孩⼦个数的最⼤值称为B树的阶,通常⽤m表示。⼀棵m阶B树或为空树,或为满⾜如下特性的m叉树:
- 树中每个结点⾄多有 m 棵⼦树,即⾄多含有 m-1 个关键字。
- 若根结点不是终端结点,则⾄少有两棵⼦树。
- 除根结点外的所有⾮叶结点⾄少有 ⌈ m / 2 ⌉棵⼦树,即⾄少含有 $\lceil m/2\rceil-1 $个关键字。(为了保证查找效率,每个结点的关键字不能太少)
-
所有的叶结点都出现在同⼀层次上,并且不带信息(可以视为外部结点或类似于折半查找判定树的查找失败结点,实际上这些结点不存在,指向这些结点的指针为空)。

m阶B树的核⼼特性:
- 根节点的⼦树数∈ [ 2 , m ] ∈[2, m]∈[2,m],关键字数 ∈ [ 1 , m − 1 ] ∈[1, m-1]∈[1,m−1]。
- 其他结点的⼦树数∈ [ ⌈ m / 2 ⌉ , m ] ∈[⌈m/2⌉ , m]∈[⌈m/2⌉,m];关键字数∈ [ − 1 , m − 1 ] ∈[ -1, m-1]∈[−1,m−1]。
- 对任⼀结点,其所有⼦树⾼度都相同。
- 关键字的值:⼦树0 < 关键字1 < ⼦树1 < 关键字2 < ⼦树2 <…. (类⽐⼆叉查找树左<中<右)
B树的⾼度:含 n 个关键字的 m叉B树,最⼩⾼度、最⼤⾼度是多少?
- logmn+1≤h≤log⌈m/2⌉2n+1+1
2、B树的基本操作
B树的查找:
- B树的查找操作与二叉查找树类似。B树的查找包含两个基本操作:① 在B树中找结点;② 在结点中找关键字。B树常存储在磁盘上,因此前一个查找操作在磁盘上进行,后一个查找操作在内存中进行。在B树中查找到某个结点后,先在有序表中进行查找,若找到则查找成功,否则按照对应指针信息到所指的子树中去查找。查找到叶子结点(对应指针为空指针),则说明树中没有对应的关键字,查找失败。
B树的插入:将关键字 key 插入到B树的过程:
- 定位:利用B树的查找算法,找到插入该关键字的最底层中的某个非叶子结点。(插入位置一定是最底层的某个非叶子结点!)
- 插入:B树中,每个非失败节点的关键字个数都在区间[ ⌈ m / 2 ⌉ − 1 , m − 1 ] [⌈m/2⌉- 1,m-1][⌈m/2⌉−1,m−1]内。若插入关键字 key 之后结点关键字个数小于m,则可以直接插入;否则必须对结点进行分裂。
- 分裂:从结点的中间位置(⌈ m / 2 ⌉ ⌈m/2⌉⌈m/2⌉)将其中的关键字分为两部分,左半部分包含的关键字放到原结点中,右半部分包含的关键字放到新节点中,中间位置(⌈ m / 2 ⌉ ⌈m/2⌉⌈m/2⌉)的关键字则插入原节点的父节点。若此时父节点的关键字也超过了上限,则对父节点继续进行分裂操作,直到这个过程传到根节点为止,进而导致B树的高度增加。
B树的删除:
- 非终端结点的删除:使用直接前驱或者直接后继来代替被删除的关键字,转换为删除终端结点。
- 终端结点的删除,具体分为三种情况
- 直接删除关键字:若删除关键字所在结点关键字个数 ≥ ⌈ m / 2 ⌉ ≥⌈m/2⌉≥⌈m/2⌉,则可直接删除。
- 兄弟够借:若删除关键字所在结点关键字个数 = ⌈ m / 2 ⌉ − 1 =⌈m/2⌉-1=⌈m/2⌉−1,且与此结点相邻的左(或右)兄弟结点关键字个数 ≥ ⌈ m / 2 ⌉ ≥⌈m/2⌉≥⌈m/2⌉,则需调整该节点、左(或右)兄弟结点及其双亲结点(父子换位法)以达到新的平衡。
- 兄弟不够接:若删除关键字所在结点关键字个数 = ⌈ m / 2 ⌉ − 1 =⌈m/2⌉-1=⌈m/2⌉−1,且与此结点相邻的左(或右)兄弟结点关键字个数 = ⌈ m / 2 ⌉ − 1 =⌈m/2⌉-1=⌈m/2⌉−1,则将该节点、左(或右)兄弟结点及其双亲结点中的关键字进行合并。
3、B+树
一棵m阶的B+树需满足以下条件:
- 每个分支节点最多有m棵子树(孩子结点)。
- 非叶根结点至少有两颗子树,其他每个分支结点至少有⌈ m / 2 ⌉ ⌈m/2⌉⌈m/2⌉棵子树。
- 结点的子树个数与关键字个数相同。
- 所有叶子结点包含所有关键字及指向相应记录的指针,叶子结点中将关键字按大小排列,并且相邻叶子结点按大小顺序相互链接起来。(说明B+树支持顺序查找)
- 所有分支节点仅包含它的各个节点中关键字的最大值及指向其子节点的指针。
4、散列查找及其性能分析
散列表的基本概念
- 散列函数:一个把查找表中的关键字映射成该关键字对应的地址的函数,记作H a s h ( k e y ) = A d d r Hash(key)=AddrHash(key)=Addr。
- 散列函数可能会把两个或两个以上的不同关键字映射到同一地址,称这种情况为冲突。发生碰撞的不同关键字称为同义词。
- 散列表:根据关键字而直接进行访问的数据结构。散列表建立了关键字和存储地址之间的一种直接映射关系。
散列函数的构造方法
- 直接定址法:直接取关键字的某个线性函数值为散列地址,散列函数为 H ( k e y ) = k e y 或 H ( k e y ) = a × k e y + b 。这种方法计算简单,不会产生冲突。缺点是空位较多,会造成存储空间浪费。
- 除留余数法:假定散列表表长 m,取一个不大于但最接近 m 的质数 p,利用散列函数 H ( k e y ) = k e y % p将关键字转换为散列地址。p取质数是因为这样可以使关键字通过散列函数转换后等概率地映射到散列空间上的任一地址。
- 数字分析法:假设关键字是 r进制数,而r个数码在个位上出现的频率不一定相同,可能在某些位上分布的均匀一些,而在某些位分布的不均匀。此时应选数码分布均匀的若干位作为散列地址。
- 平方取中法:这种方法取关键字平方值的中间几位作为散列地址,具体取多少位视具体情况而定。这种方法得到的散列地址与关键字的每一位都有关系,因此使得散列地址分布比较均匀。适用于关键字每位取值都不够均匀或均小于散列地址所需的位数。
5、散列查找及性能分析
散列查找执行步骤如下
- 初始化:A d d r = H a s h ( k e y )
- 检测查找表中地址为 Addr 的位置上是否有记录,若无记录,返回查找失败;若有记录,比较它和 key 的值,若相等则返回查找成功,否则执行步骤③。
- 用给定的处理冲突方式计算“下一个散列表地址”,并把 Addr 置为此地址,转入步骤②。
平均查找长度(ASL):散列表查找成功的平均查找长度即找到表中已有表项的平均比较次数;散列表查找失败的平均查找长度即找不到待查的表项但能找到插入位置的平均比较次数。
相关文章:

【王道数据结构】第七章| 查找 | 树
目录 一、查找 1、查找概念 2、顺序查找 3、折半查找 4、分块查找 二、树 1、B树 2、B树的基本操作 3、B树 4、散列查找及其性能分析 5、散列查找及性能分析 一、查找 1、查找概念 查找:在数据集合中寻找满足某种条件的数据元素的过程称为查找。查找…...

VBA提高篇_19 可选参数Optional_ IsMissing _MSgbox
文章目录1. 可选参数Optional2.IsMissing判断参数是否提供,只能判断变体类型3. 使用 : 可以按参数名传递参数 a:1,c:34.Msgbox 常用参数5.VBA颜色常量表1. 可选参数Optional Optional 代表本参数是可选项 False ; 代表参数若不指定,则默认为False Function mySumProduct(r As R…...

【子网划分】求子网网络前缀、子网地址、每个子网可以分配给主机使用的最小地址和最大地址
1、某单位分配到一个地址块152.7.77.0/24,现在需要进一步划分为4个一样大的子网。(10分) 问题: (1) 每个子网的网络前缀有多长? (2) 每一个子网中有多少个地址? (3) 每一个子网的网络地址是什么?…...
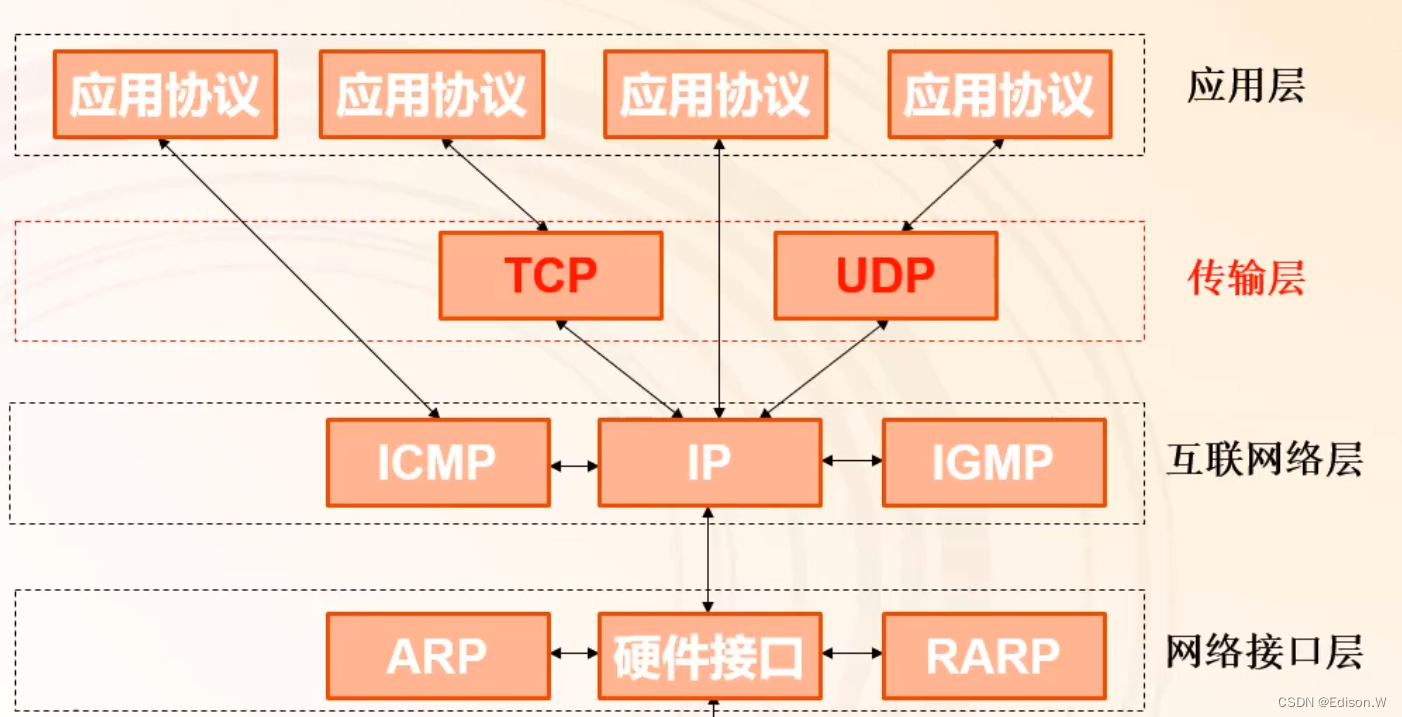
网络协议安全
网络协议安全网络协议ISO/OSI七层模型OSI模型与TCP/IP模型网络接口与互联网层安全传输层与应用层安全传输层协议-TCP协议传输层协议-UDP协议网络协议 ISO/OSI七层模型 物理层 作用:定义物理链路的前期、机械、通信规程、功能要求等将比特流庄换成电压典型物理层设备…...

ImportError: /lib64/libm.so.6: version `GLIBC_2.23‘ not found问题解决方法
1.环境:Centos7,GCC version 9.1.0,python3.7,TensorFlow1.14.0.因为/usr/lib64/libstdc.so.6: version CXXABI_1.3.8 not found问题,我将GCC版本升级到了9.1.0,但是运行TensorFlow的时候出现了ImportError…...

盂县基本情况
寒假的活动报告,万物皆可CSDN,贴一下吧 盂县隶属于阳泉市,阳泉市是李彦宏和刘慈欣的家乡,阳泉市内有百度云计算中心 基本情况 盂县,隶属山西省阳泉市,地处山西省东部、太行山西麓,东与河北省平…...
VC++打开或关闭目标进程的声音(扬声器)(附源码)
VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...&a…...

LeetCode 每日一题 2023/1/23-2023/1/29
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录1/23 2303. 计算应缴税款总额1/24 1828. 统计一个圆中点的数目1/25 1632. 矩阵转换后的秩1/26 1663. 具有给定数值的最小字符串1/27 2309. 兼具大小写的最好英文字母1/28 16…...

Hadoop组件Yarn常见命令
Hadoop组件Yarn常见命令 一、概述 当我们不能使用ResourceManager Web UI时,就需要使用Yarn命令来处理问题。因此,我们需要了解如何使用yarn命令监控YARN集群。 Hadoop的yarn命令具有广泛的使用范围: 它可以帮助我们管理大量的MR、Spark、Flink任务。例如获取和杀死正在运…...
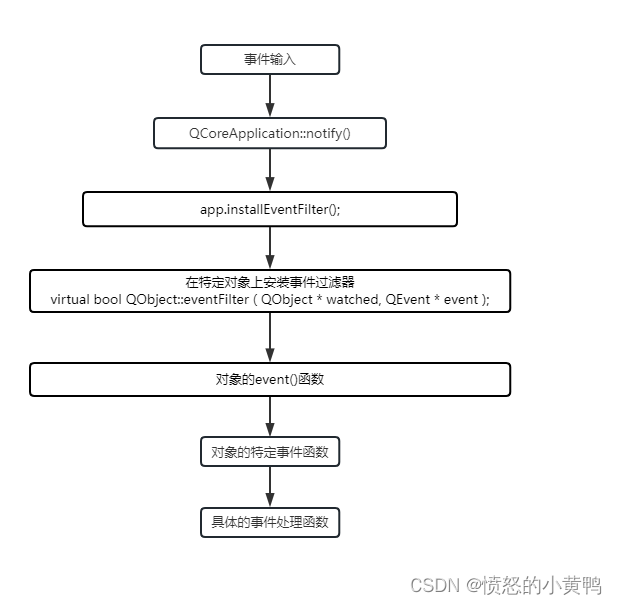
QT之事件系统
QT之事件系统1. 概述2. 事件的传递3. 事件类型4. 事件处理与事件过滤5. 自定义事件5.1 Demo6. 发送事件7. 参考1. 概述 在QT中,事件均派生自QEvent抽象类,事件可以由任何派生自QObject的子类实例接收和处理。它们与widget关联性极强。 2. 事件的传递 …...

Python中__init__.py文件深入理解
Python中文件__init__.py深入理解1. 简介1.1 模块(Module)和包(Package)的概念1.2 __init__.py文件简介2. __init__.py内容写法2.1 __init__.py文件内容2.2 __init__.py内容解释1. 简介 1.1 模块(Module)和…...
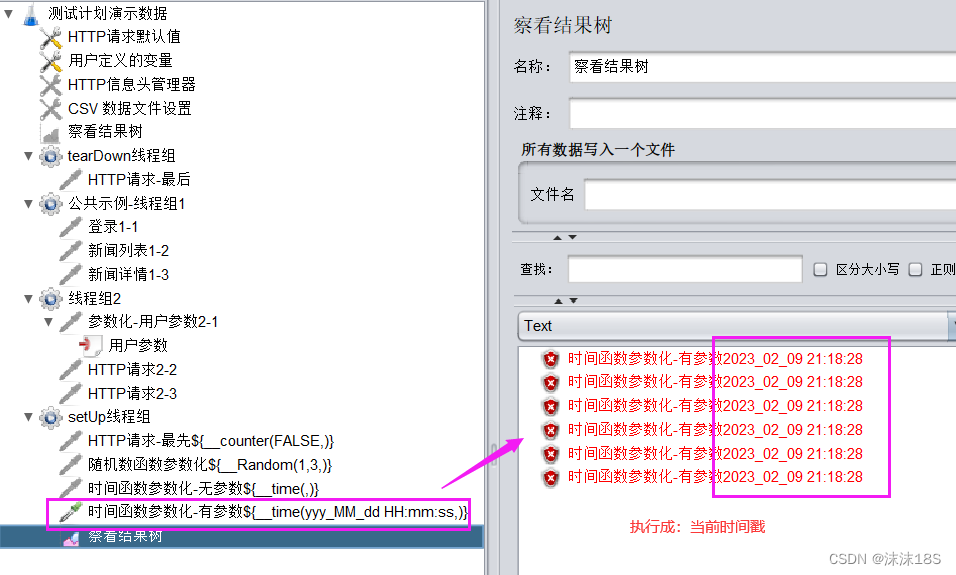
Jmeter之实现参数化的不同方式详解
参数化简介 定义:动态的获取、设置或生成数据,是一种由程序驱动代替人工驱动的数据设计方案,提高脚本的编写效率以及编写质量 适用场景:当提交的数据量较大时,每次修改太麻烦,可以使用参数化 本文介绍实现…...
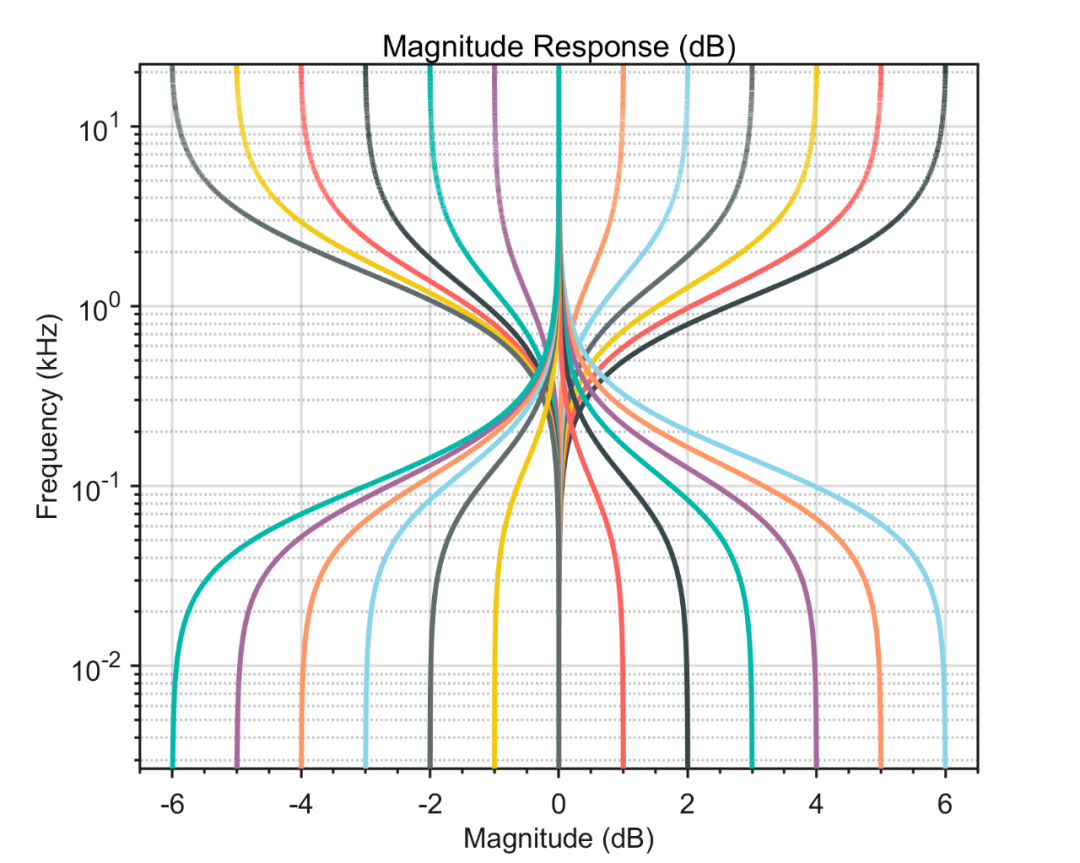
Matlab论文插图绘制模板第76期—半对数刻度折线图(Semilogx和Semilogy)
在之前的文章中,分享了Matlab双对数刻度折线图的绘制模板: 进一步,再来分享一下半对数刻度折线图的绘制模板。 先来看一下成品效果: 特别提示:Matlab论文插图绘制模板系列,旨在降低大家使用Matlab进行科研…...

【找工作】永善县政务服务管理局公开招聘5名公益性岗位人员
【找工作】永善县政务服务管理局公开招聘5名公益性岗位人员 为贯彻落实《中华人民共和国就业促进法》《就业服务和就业管理规定》,帮助有劳动能力和就业愿望的就业困难人员实现就业,永善县政务服务管理局拟向社会公开招聘公益性岗位人员5名,…...
)
【C++】从0到1入门C++编程学习笔记 - 提高编程篇:STL常用算法(拷贝和替换算法)
文章目录一、copy二、replace三、replace_if四、swap学习目标: 掌握常用的拷贝和替换算法 算法简介: copy // 容器内指定范围的元素拷贝到另一容器中replace // 将容器内指定范围的旧元素修改为新元素replace_if // 容器内指定范围满足条件的元素替换…...

C语言程序环境剖析——探究从.c到.exe之路
程序环境1.程序的翻译环境和执行环境2. 详解编译 链接2.1 翻译环境2.2 编译的三部分预编译编译汇编2.3链接3.运行环境1.程序的翻译环境和执行环境 在ANSI C的任何一种实现中,都存在两个不同的环境。 翻译环境,在这个环境中源代码被转换成可执行的机器指…...
【软件测试】8年资深测试总结出的测试学习经验,从入门到测试开发......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 测试圈子里有一句话…...

【博学谷学习记录】超强总结,用心分享|Spark的RDD算子分类
概念 RDD(Resilient Distributed Dataset)叫做弹性分布式数据集,是Spark中最基本的数据抽象,代表一个不可变、可分区、里面的元素可并行计算的集合,它是一种抽象的数据模型,本身并不存储数据,仅…...
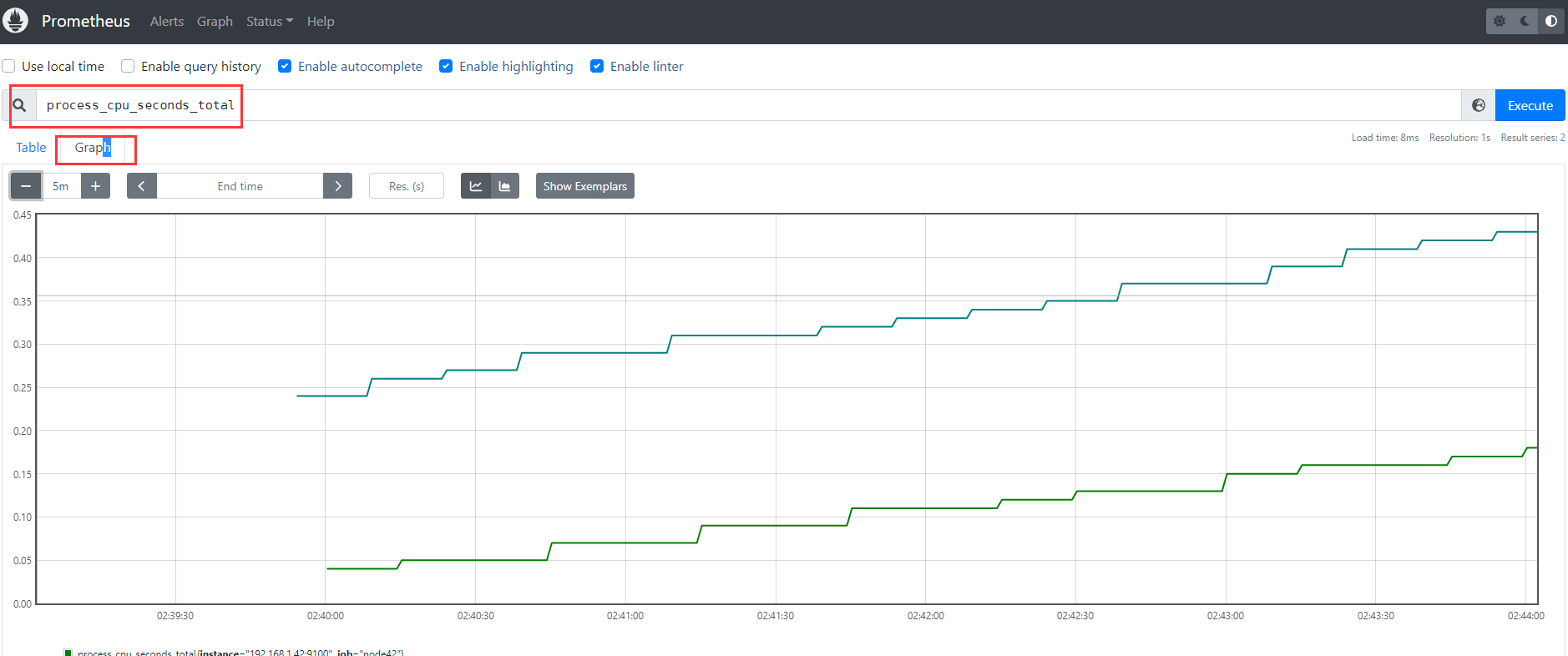
云原生系列之使用 prometheus监控远程主机实战
文章目录前言一. 实验环境二. 安装node_exporter2.1 node_exporter的介绍2.2 node_exporter的安装三. 在prometheus服务端配置监控远程主机3.1 在server端配置拉取node的信息3.2 重启prometheus3.3 通过浏览器查看prometheus总结前言 大家好,又见面了,我…...
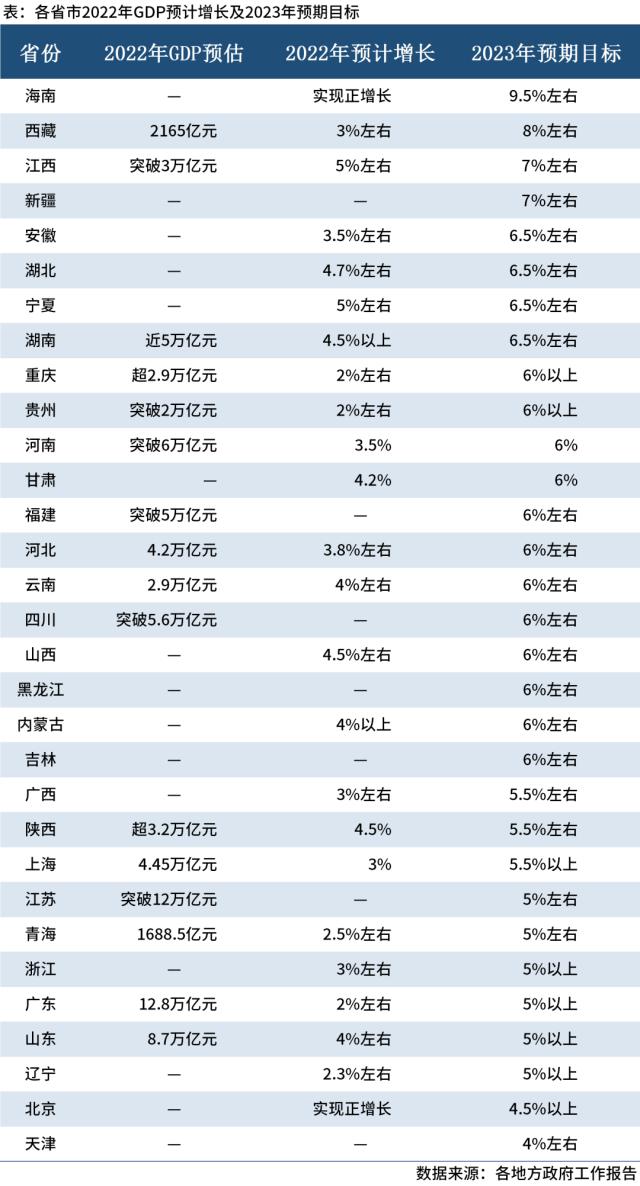
2023年地方两会政府工作报告汇总(各省市23年重点工作)
新年伊始,全国各地两会密集召开,各省、市、自治区2023年政府工作报告相继出炉,各地经济增长预期目标均已明确。相较于2022年,多地经济增长目标放缓,经济不断向“高质量”发展优化转型。今年是二十大后的开局之年&#…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

