运筹系列83:使用分枝定界求解tsp问题
1. 辅助函数
Node算子用来存储搜索树的状态。其中level等于path的长度,path是当前节点已经访问过的vertex清单,bound则是当前的lb。
这里的bound函数是一种启发式方法,等于当前路径的总长度,再加上往后走两步的最小值。
struct Nodelevel::Intpath::Vector{Int64} bound::Int
endfunction totaldist(adj_mat::Array{Int64,2},t::Vector{Int64} )n = length(t)sum([adj_mat[t[i],t[i+1]] for i in 1:n-1])+adj_mat[t[n],t[1]]
endfunction bound(adj_mat::Array{Int64,2}, path::Vector{Int64} )_bound = 0n = size(adj_mat)[1]determined, last = path[1:end-1], path[end]remain = setdiff(1:n,path)for i in 1:length(path)-1;_bound += adj_mat[path[i],path[i + 1]];end_bound += minimum([adj_mat[last,i] for i in remain])p = [path[1];remain]for r in remain_bound+=minimum([adj_mat[r,i] for i in setdiff(p,r)])endreturn _bound
end;
2. 分枝定界代码
这里用priorityQueue存储节点,用Queue也是一样的。
分枝条件为bound<ub,往下搜索所有没有探访过的节点,使用函数setdiff(1:n,v.path)。当然这里可以尝试将搜索范围缩小,比如仅搜索最近的一些节点,不过就不保证最优性了。
当搜索到level==n-1时,获得一个可行解,并且停止往下探索。此时如果路径长度比ub还短,则更新ub。
function solve(adj_mat::Array{Int64,2},ub::Int64 = 10^9)optimal_tour = Vector{Int64}()optimal_length = 0n = size(adj_mat)[1]PQ = PriorityQueue{Node,Int}()path = Vector{Int64}([1])v = Node(1,path,bound(adj_mat,path))enqueue!(PQ,v,v.bound) while length(PQ)>0v = dequeue!(PQ)if v.bound<ublevel = v.level+1b = 0for i in setdiff(1:n,v.path)path = [v.path;i]if level==n-1 #终止条件push!(path,setdiff(1:n,path)[1])_len = totaldist(adj_mat,path)if _len < ubub = _lenoptimal_length = _lenoptimal_tour = pathendelse # 进行分叉b = bound(adj_mat,path)if b < ub # 分枝条件enqueue!(PQ,Node(level,path,b),b)endendendendendoptimal_tour,optimal_length
end
solve([0 14 4 10 20;14 0 7 8 7;4 5 0 7 16;11 7 9 0 2;18 7 17 4 0])
输出([1, 4, 5, 2, 3], 30)。
TSP时一个NPhard问题,当点数增多时,使用b&b的算法性能会急速下降。
相关文章:

运筹系列83:使用分枝定界求解tsp问题
1. 辅助函数 Node算子用来存储搜索树的状态。其中level等于path的长度,path是当前节点已经访问过的vertex清单,bound则是当前的lb。 这里的bound函数是一种启发式方法,等于当前路径的总长度,再加上往后走两步的最小值。 struct …...
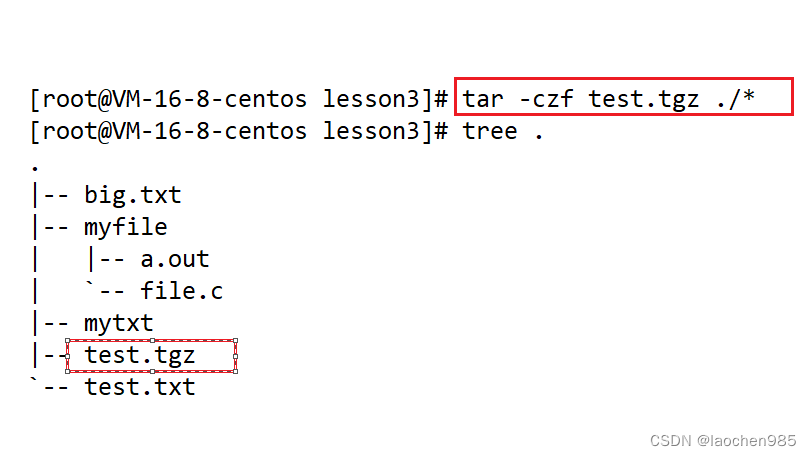
linux 指令 第3期
cat cat 指令: 首先我们知道一个文件内容属性 我们对文件操作就有两个方面:对文件内容和属性的操作 扩展:echo 指令 直接打印echo后面跟的字符串 看: 这其实是把它打印到了显示器上,我们也可以改变一下它的打印位置…...
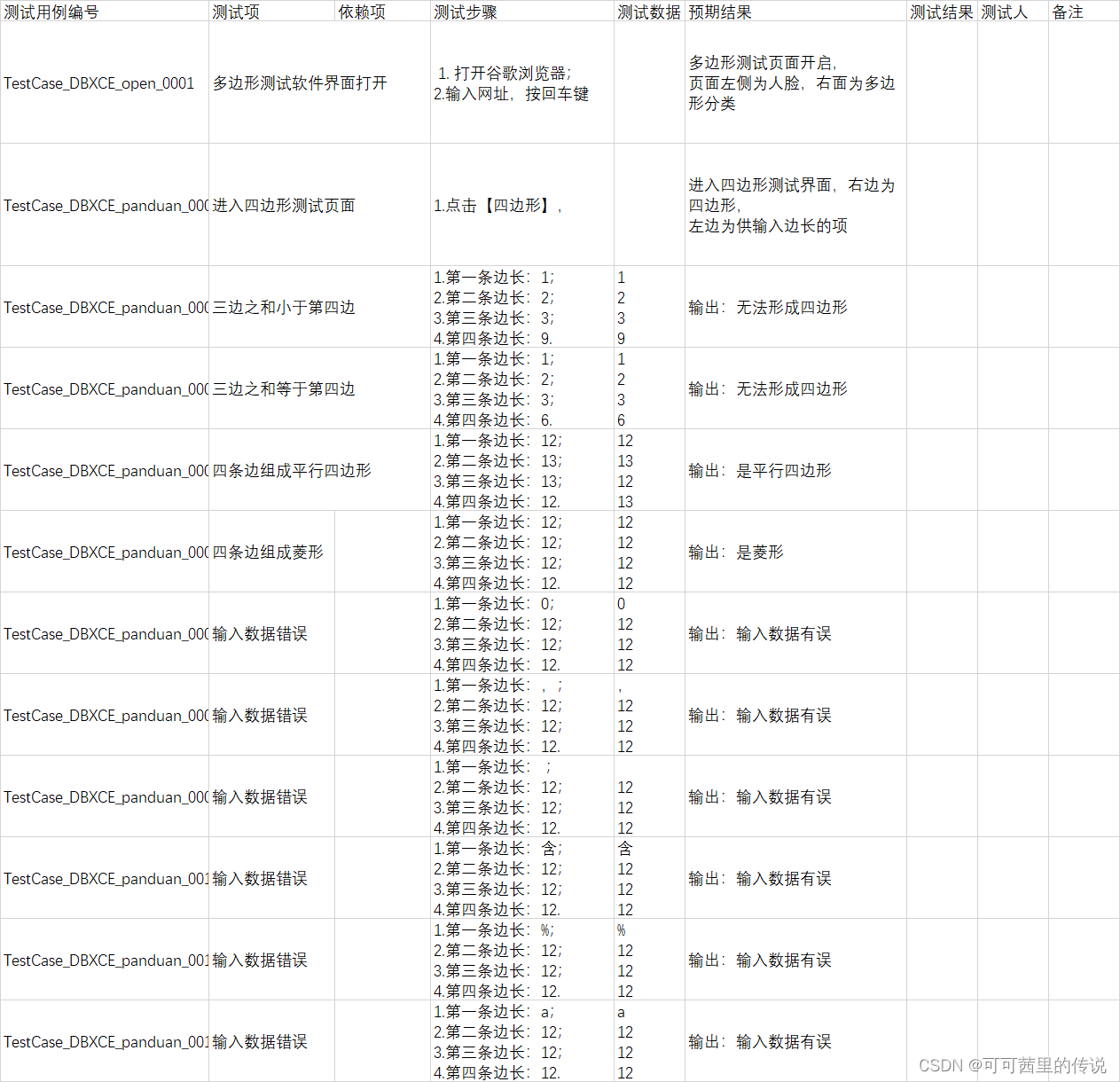
测试用例实战
测试用例实战 三角形判断 三角形测试用例设计 测试用例编写 先做正向数据,再做反向数据。 只要有一条边长为0,那就是不符合要求,不需要再进行判断,重复。 四边形 四边形测试用例...

Unity XML1——XML基本语法
一、XML 概述 全称:可拓展标记语言(EXtensible Markup Language) XML 是国际通用的,它是被设计来用于传输和存储数据的一种文本特殊格式,文件后缀一般为 .xml 我们在游戏中可以把游戏数据按照 XML 的格式标…...

了解Unity编辑器之组件篇Playables和Rendering(十)
Playables 一、Playable Director:是一种用于控制和管理剧情、动画和音频的工具。它作为一个中央控制器,可以管理播放动画剧情、视频剧情和音频剧情,以及它们之间的时间、顺序和交互。 Playable Director组件具有以下作用: 剧情控…...
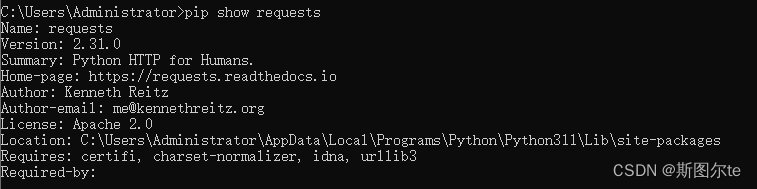
python的包管理器pip安装经常失败的解决办法:修改pip镜像源
pip 常用的国内镜像源: https://pypi.tuna.tsinghua.edu.cn/simple/ // 清华 http://mirrors.aliyun.com/pypi/simple/ // 阿里云 https://pypi.mirrors.ustc.edu.cn/simple/ // 中国科技大学 http://pypi.hustunique.com/ // 华中理…...
忘记安卓图案/密码锁如何解锁?
如何解锁Android手机图案锁?如何删除忘记的密码?Android 手机锁定后如何重置?这是许多智能手机用户在网上提出的几个问题。为了回答这些问题,我们想出了一些简单有效的方法来解锁任何设备而不丢失数据。 忘记手机密码可能会令人恐…...
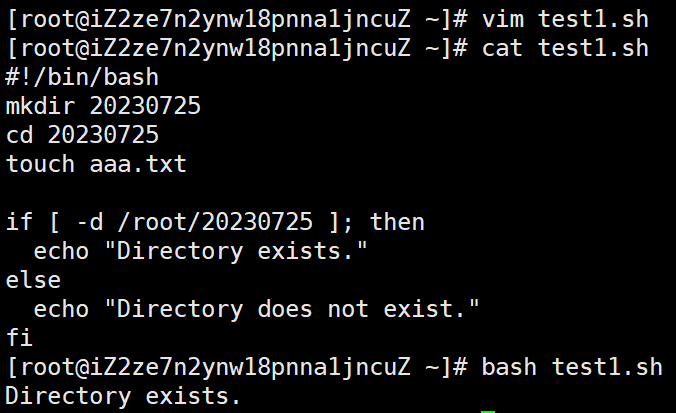
Bash编程
目录: bash编程语法bash脚本编写 1.bash编程语法 Bash 编程基础 变量引号数组控制语句函数 Bash 变量 语法: Variable_namevalue Bash 变量定义的规则 变量名区分大小写,a和A为两个不同的变量。变量名可以使用大小写字母混编的形式进行…...

vue指令-v-model修饰符
vue指令-v-model修饰符 1、目标2、语法 1、目标 让v-modelv-mode拥有更强大的功能 2、语法 v-model.修饰符“Vue数据变量” .number 以parseFloat转成数字类型 .trime 去除首位空白字符 .lazy 在change时触发而非input时示例1 <template><div id"app"&g…...

【论文精读CVPR_2023】3D-Aware Face Swapping
【论文精读CVPR_2023】3D-Aware Face Swapping 前言Abstract1. Introduction2. Related WorkFace Swapping.3D-Aware Generative Models.GAN Inversion.3. Method3.1. Overview3.2. Inferring 3D Prior from 2D Images3.3. Face Swapping via Latent Code Manipulation3.4. Joi…...

flutter开发实战-自定义相机camera功能
flutter开发实战-自定义相机camera功能。 Flutter 本质上只是一个 UI 框架,运行在宿主平台之上,Flutter 本身是无法提供一些系统能力,比如使用蓝牙、相机、GPS等,因此要在 Flutter 中调用这些能力就必须和原生平台进行通信。 实现…...

重排链表——力扣143
文章目录 题目描述法一:寻找链表中点、链表逆序、链表合并 题目描述 法一:寻找链表中点、链表逆序、链表合并 void reorderList(ListNode* head){if(headnullptr){return;}// 找到中点 ListNode* mid FindMiddle(head);ListNode *h1head, *h2mid->ne…...
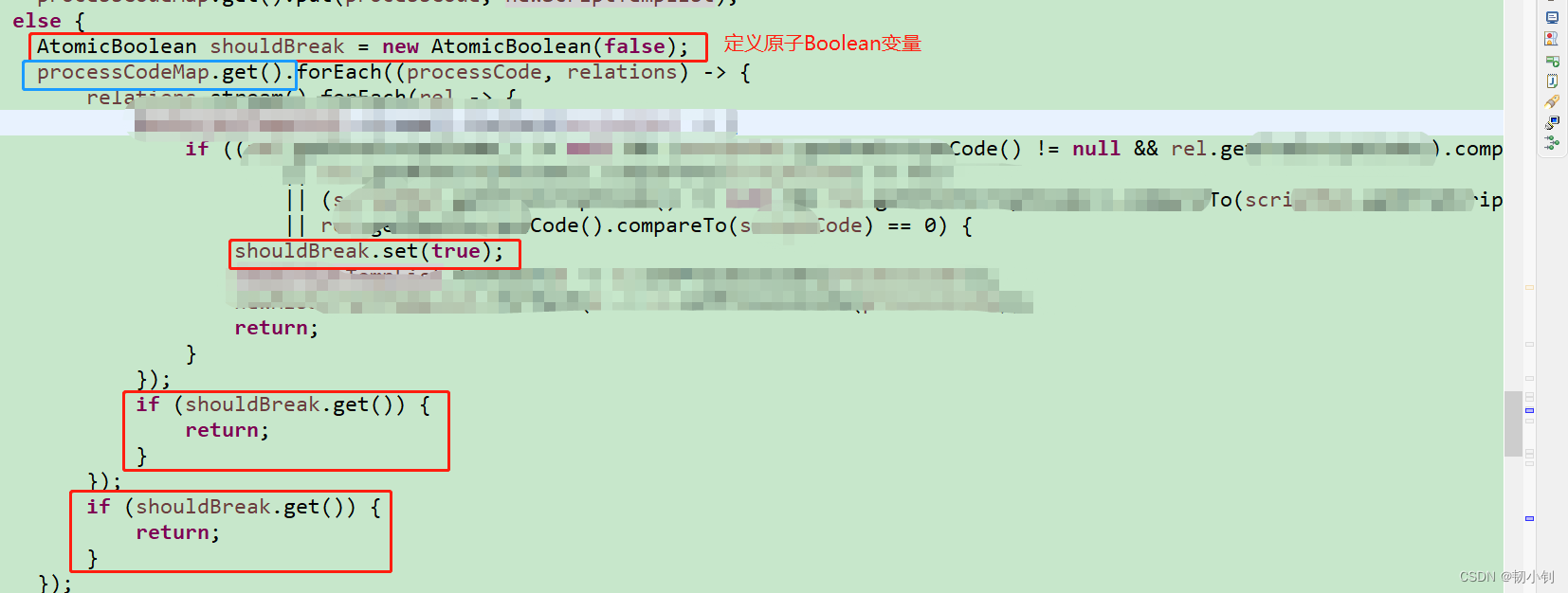
Lambda表达式常见的Local variable must be final or effectively final原因及解决办法
目录 Local variable must be final or effectively final错误原因 解决办法按照要求定义为final(不符合实情,很多时候是查库获取的变量值)使用原子类存储变量,保证一致性AtomicReference常用原子类 其它 Local variable must be …...

YOLOv5改进系列(16)——添加EMA注意力机制(ICASSP2023|实测涨点)
【YOLOv5改进系列】前期回顾: YOLOv5改进系列(0)——重要性能指标与训练结果评价及分析 YOLOv5改进系列(1)——添加SE注意力机制 YOLOv5改进系列(2)——添加...
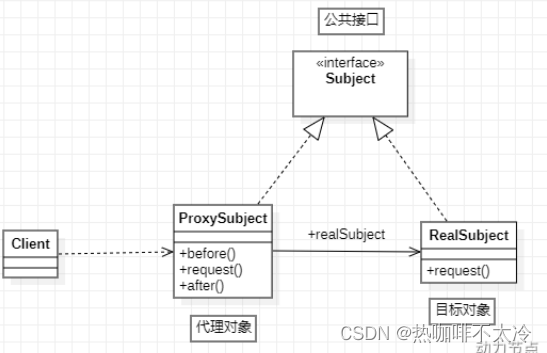
[SSM]GoF之代理模式
目录 十四、GoF之代理模式 14.1对代理模式的理解 14.2静态代理 14.3动态代理 14.3.1JDK动态代理 14.3.2CGLIB动态代理 十四、GoF之代理模式 14.1对代理模式的理解 场景:拍电影的时候,替身演员去代理演员完成表演。这就是一个代理模式。 演员为什…...
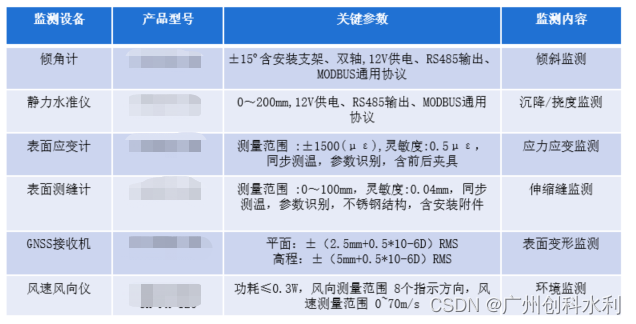
桥梁安全生命周期监测解决方案
一、方案背景 建筑安全是人们生产、经营、居住等经济生活和人身安全的基本保证,目前我国越来越多的建筑物逐 步接近或者已经达到了使用年限,使得建筑物不断出现各种安全隐患,对居民的人身安全和财产安全产 生不利影响,因此房…...
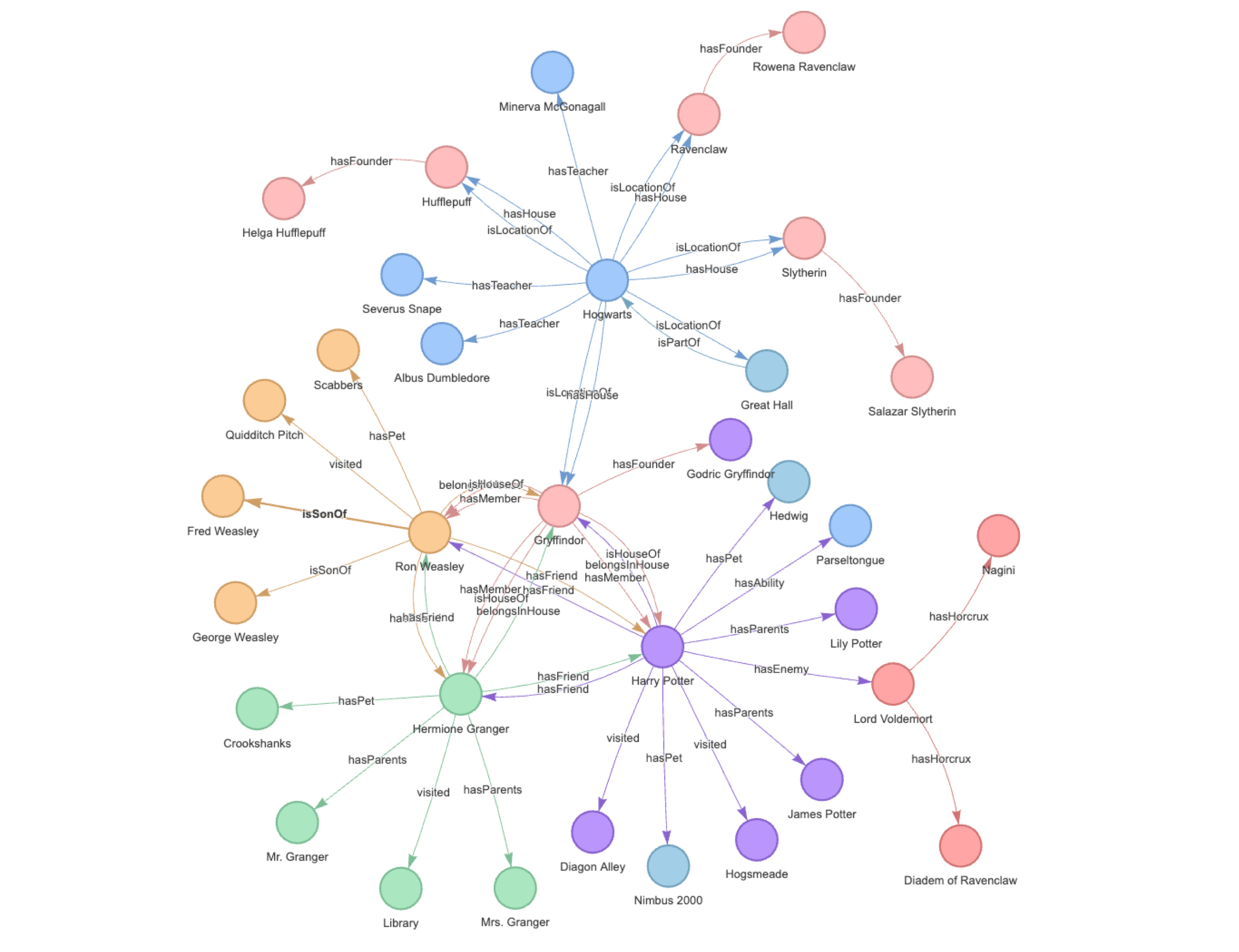
图技术在 LLM 下的应用:知识图谱驱动的大语言模型 Llama Index
LLM 如火如荼地发展了大半年,各类大模型和相关框架也逐步成型,可被大家应用到业务实际中。在这个过程中,我们可能会遇到一类问题是:现有的哪些数据,如何更好地与 LLM 对接上。像是大家都在用的知识图谱,现在…...
)
SpringBoot自动配置、启动器原理爆肝解析(干货满满)
文章目录 前言一、SpringBoot优势概要二、SpringBoot自动配置1. ☠注意☠2.自动配置详解 三、Starter(场景启动器)原理总结 前言 本文详细解析面试重点—SpringBoot自动配置原理、场景启动器原理,深入源码,直接上干货、绝不拖泥带…...

chrome扩展控制popup页面动态切换
文章目录 1、通过控制元素的显示隐藏达到popup页面切换的效果2、通过监听页面重新加载完成不同popup的切换3、直接修改popup页面location.href,无需刷新页面 1、通过控制元素的显示隐藏达到popup页面切换的效果 下面在mv2版本的API下完成 实际上通过控制页面元素实…...
:PyTorch常用函数)
【AI】《动手学-深度学习-PyTorch版》笔记(三):PyTorch常用函数
AI学习目录汇总 1、torch.arange 返回一维张量(一维数组),官网说明,常见的三种用法如下 输入:torch.arange(5) 输出:tensor([0, 1, 2, 3, 4]) 输入:torch.arange(5, 16) 输出:tensor([ 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]) 输入:torch.arange(1, 25, 2) …...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
