24考研数据结构-第二章:线性表
目录
- 第二章:线性表
- 2.1线性表的定义(逻辑结构)
- 2.2 线性表的基本操作(运算)
- 2.3 线性表的物理/存储结构(确定了才确定数据结构)
- 2.3.1 顺序表的定义
- 2.3.1.1 静态分配
- 2.3.1.2 动态分配
- 2.3.1.3 malloc与free
- 2.3.2 顺序表的特点
- 2.3.3 顺序表的基本操作
- 2.3.3.1 插入操作
- 2.3.3.2 插入操作的时间复杂度
- 2.3.3.3 删除操作
- 2.3.3.4删除操作的时间复杂度
- 2.3.3.5 知识回顾与重要考点
- 2.3.3.6 顺序表的按位查找
- 2.3.3.7 顺序表按位查找的时间复杂度
- 2.3.3.8 顺序表按值查找
- 2.3.3.9顺序表按值查找的时间复杂度
- 2.3.3.10 知识回顾与重要考点
- 2.4 线性表的链式表示
- 2.4.0 引入的原因
- 2.4.1 单链表的定义
- 2.4.2 单链表的两种实现形式
- 2.4.2.1 不带头结点的单链表
- 2.4.2.2 带头结点的单链表
- 2.4.2.3知识回顾与重要考点
- 2.4.3.1 带头结点的单链表按位序插入节点
- 2.4.3.2 单链表的插入节点的时间复杂度
- 2.4.3.3 不带头结点的单链表的插入节点
- 2.4.3.4 不带头结点的单链表的插入节点的时间复杂度
- 2.4.3.5 指定节点的后插操作
- 2.4.3.6 指定节点的前插操作
- 2.4.3.7 按位序删除节点(带头结点)
- 2.4.3.8 按位序删除节点(带头结点)的时间复杂度
- 2.4.3.9 指定结点的删除
- 2.4.3.10 知识回顾与重要考点
- 2.4.4单链表的查找操作(默认带头节点,不带头节点后续更新)
- 2.4.4.1 按位查找操作
- 2.4.4.2 按值查找操作
- 2.4.4.3 求单链表的长度(带和不带头节点都写了)
- 2.4.4.4 知识回顾与重要考点
- 2.4.5 单链表的创建操作
- 2.4.5.1 头插法建立单链表
- 2.4.5.2 尾插法建立单链表
- 2.4.5.3 链表的逆置
- 2.4.6 双链表
- 2.4.6.1 双链表中节点类型的描述:
- 2.4.6.2 双链表的初始化
- 2.4.6.3 双链表的插入操作
- 2.4.6.4 双链表的删除操作
- 2.4.6.5 双链表的遍历操作
- 2.4.6.6 知识回顾与重要考点
- 2.4.7 循环链表
- 2.4.7.1 循环单链表
- 2.4.7.2 单链表和循环单链表的比较:
- 2.4.7.3 循环双链表
- 双链表的插入(循环双链表):
- 双链表的删除
- 2.4.7.4 知识回顾与重要考点
- 2.4.8 静态链表
- 2.4.9 顺序表和链表的比较
- 2.4.9.1 逻辑结构
- 2.4.9.2 存储结构
- 2.4.9.3 基本操作 - 创建
- 2.4.9.4 基本操作 - 销毁
- 2.4.9.5 基本操作-增/删
- 2.4.9.6 基本操作-查
- 2.4.9.7 顺序、链式、静态、动态四种存储方式的比较
- 2.4.9.8 存储密度的问题
- 2.4.9.9 存储方式的选择以及二者优劣的答题思路(综述优劣,细谈情况)
第二章:线性表
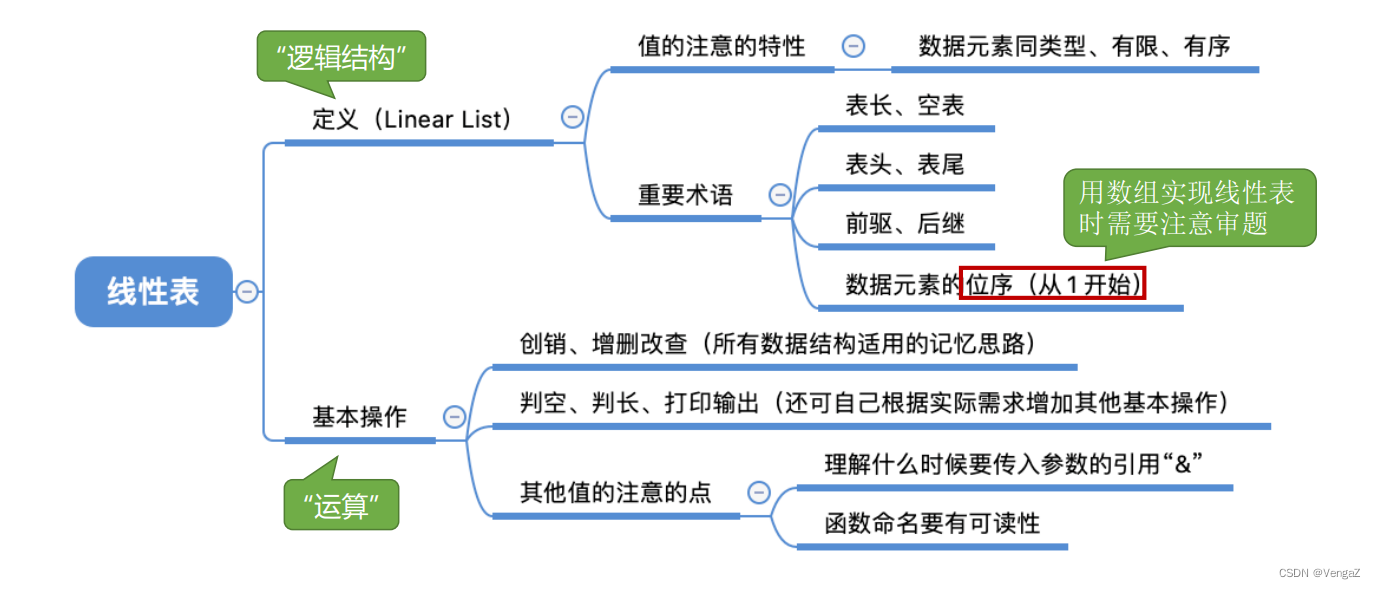
2.1线性表的定义(逻辑结构)
线性表是具有相同数据类型(int甚至structA自定义的结构)的n(n>0)个数据元素的有限序列,其中n为表长,当n=0时线性表是一个空表。
所有的整数按递增次序排列,不是线性表
- n = 0时,空表
- 有限、有序、相同数据结构的元素
- a i a_i ai是线性表中的“第i个”元素线性表中的位序,位序从1开始,数组下标从0开始
- a 1 a_1 a1是表头元素, a n a_n an是表尾元素
- 除了第一和最后一个元素外,每个元素都有唯一的直接前驱以及直接后继
2.2 线性表的基本操作(运算)

注:对于传参的&L以及L两种,区别在于&L是引用型,即需要修改参数的情况既需要引用。L是仅仅获取,不进行修改返回。(引用即是对参数本身进行修改,不引用即是对参数的复制进行操作)
2.3 线性表的物理/存储结构(确定了才确定数据结构)
2.3.1 顺序表的定义
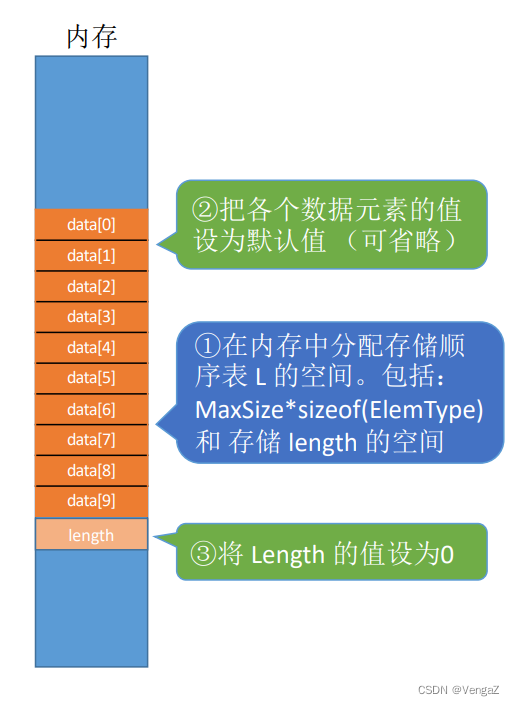
2.3.1.1 静态分配
//顺序表的实现--静态分配#include<stdio.h>
#define MaxSize 10 //定义表的最大长度
typedef struct{int data[MaxSize];//用静态的"数组"存放数据元素int length; //顺序表的当前长度
}SqList; //顺序表的类型定义(静态分配方式)
void InitList(SqList &L){for(int i=0;i<MaxSize;i++){L.data[i]=0; //将所有数据元素设置为默认初始值}L.length=0;
}
int main(){SqList L;//声明一个顺序表InitList(L);//初始化一个顺序表for(int i=0;i<MaxSize;i++){printf("data[%d]=%d\n",i,L.data[i]);}return 0;
}
void InitList(SqList &L){//for(int i=0;i<MaxSize;i++){//L.data[i]=0; //将所有数据元素设置为默认初始值//不设置数据元素的默认值}L.length=0;
}
会有历史遗留的脏数据,需要重新定义。对于数据初始化是编译器做的,不同的编译器可能会有脏数据也可能不会有

2.3.1.2 动态分配
//顺序表的实现——动态分配
#include<stdio.h>
#include<stdlib.h>//malloc、free函数的头文件
#define InitSize 10 //默认的最大长度
typedef struct{int *data;//指示动态分配数组的指针int MaxSize; //顺序表的最大容量int length; //顺序表的当前长度
}SeqList;
//初始化
void InitList(SeqList &L){//用malloc 函数申请一片连续的存储空间L.data =(int*)malloc(InitSize*sizeof(int)) ;L.length=0;L.MaxSize=InitSize;
}
//增加动态数组的长度
void IncreaseSize(SeqList &L,int len){int *p=L.data;L.data=(int*)malloc((L.MaxSize+len)*sizeof(int));for(int i=0;i<L.length;i++){L.data[i]=p[i]; //将数据复制到新区域 }L.MaxSize=L.MaxSize+len; //顺序表最大长度增加lenfree(p); //释放原来的内存空间 }
int main(void){SeqList L; //声明一个顺序表InitList(L);//初始化顺序表IncreaseSize(L,5);return 0;
}2.3.1.3 malloc与free
malloc和free 基本概念及用法: link
void* malloc(size_t size);void free(void* ptr);
-
malloc 函数用于在运行时动态分配内存。
-
malloc 接受一个 size_t 类型的参数 size,表示需要分配的内存大小(以字节为单位)。它返回一个指向分配内存起始位置的指针,或者在分配失败时返回 NULL。
-
free 函数用于释放通过 malloc 或类似函数分配的内存。
-
free 接受一个指向动态分配内存的指针 ptr,并将该内存块释放回操作系统,以便其他程序可以使用它。在释放内存后,应确保不再使用指向该内存块的指针,以避免悬挂指针的问题。
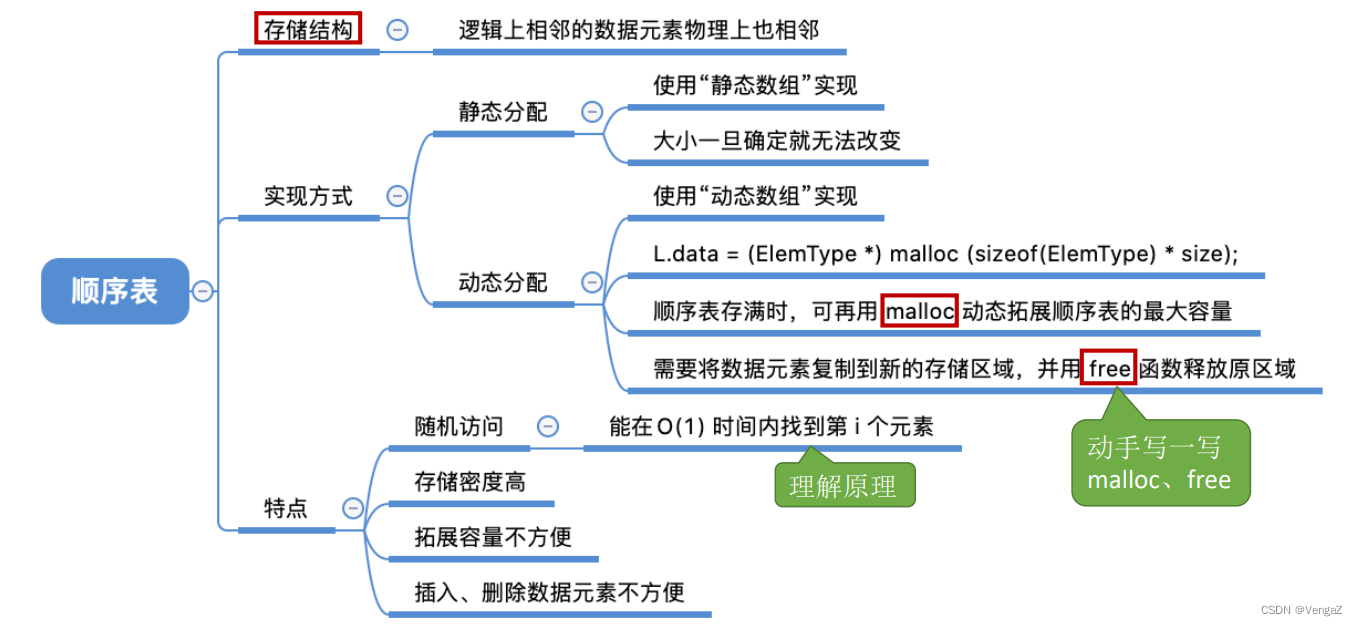
2.3.2 顺序表的特点
- 随机访问 ,可以在O(1)时间内找到第i个元素。
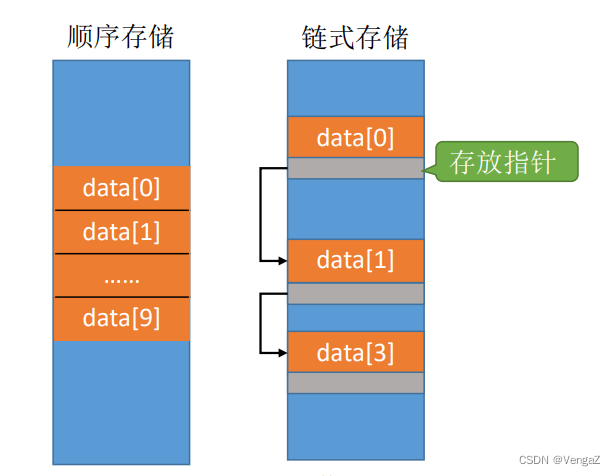
- 存储密度高,每个节点只存储数据元素,只存储数据本身,与链式存储(还需要存储指针)相比,存储密度高
- 拓展容量不方便(即使采用动态分配的方式实现,拓展长度的时间复杂度也比较高,增长长度之后得到了新的存储空间,新的动态分配的指针,所以需要将数据复制到新的空间)
- 插入、删除操作不方便,需要移动大量元素(顺序存储,所以删掉中间的一个需要将后边所有的元素都往前移动一个位置,增加同理)
2.3.3 顺序表的基本操作
2.3.3.1 插入操作
bool ListInsert(SqList &L, int i, int e){ //判断i的范围是否有效if(i<1||i>L.length+1) return false;if(L.length>MaxSize) //当前存储空间已满,不能插入 return false;for(int j=L.length; j>=i; j--){ //将第i个元素及其之后的元素后移L.data[j]=L.data[j-1];}L.data[i-1]=e; //在位置i处放入eL.length++; //长度加1return true;
}- 注意:
- 1.数组下标与顺序表的下标,需要加入元素的第i号位置,对应的数组的位置时i-1,所以将e的值赋值给L.data[i-1],也就是顺序表的第i号位置(L.data[i-1]=e)
- 2.判断i的值是否有效(i<1||i>L.length+1) ,目的是防止用户在顺序表的小于1的位置插入元素(顺序表下标从1开始),并且只能在L.length+1的范围以内(当前长度+1即下一位,也不会空元素)插入元素,即元素之间不能空。
- 3.(L.length>MaxSize),不能让顺序表的长度大于最大长度,但是可以等于
2.3.3.2 插入操作的时间复杂度
循环:for(int j=L.length; j>=i; j–)
最好情况:新元素插入表尾,i = n+1,不用移动元素 O(1)
最坏情况:新元素插入表头,i = 1,全部元素n都需要移动 O(n)
平均情况:插入每一个位置的概率都是相等的,有n +1 个位置可以插入,所以是
1 n + 1 = p \frac {1} {n+1}=p n+11=p, n ( n + 1 ) 2 ∗ p = n 2 \frac{n(n+1)}{2}*p=\frac{n}{2} 2n(n+1)∗p=2n,所以O(n)

2.3.3.3 删除操作
bool LisDelete(SqList &L, int i, int &e){ // e用引用型参数 初始值可以设置位-1//判断i的范围是否有效if(i<1||i>L.length) return false;e = L.data[i-1] //将被删除的元素赋值给efor(int j=L.length; j>=i; j--){ //将第i个后的元素前移L.data[j-1]=L.data[j];}L.length--; //长度减1return true;
}- 注意:
- 1.e是引用类型的,所以才能返回到main函数里边,倘若不是引用类型则会赋值给内存中main函数的e的一个复制,也就是不能在main函数里打印输出,L与&L同理。
- 2.(i<1||i>L.length) 是传参i的一个合法性检验,这时的i还是不能小于1,并且最大只能跟顺序表的 length一样大,不能跟插入一样修改下一位 length+1。
2.3.3.4删除操作的时间复杂度

2.3.3.5 知识回顾与重要考点
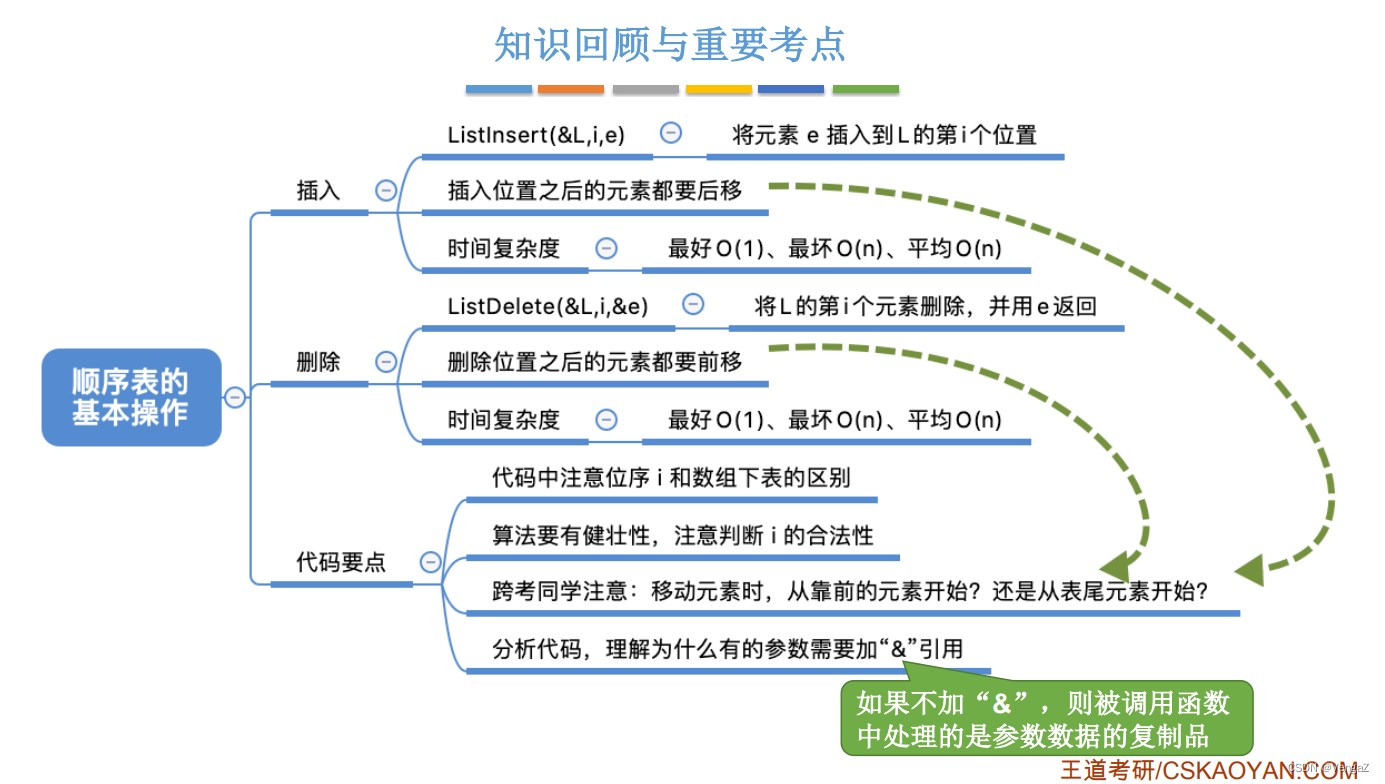
2.3.3.6 顺序表的按位查找
#define MaxSize 10 //定义最大长度
typedef struct{ElemType data[MaxSize]; //用静态的“数组”存放数据元素 int Length; //顺序表的当前长度
}SqList; //顺序表的类型定义ElemType GetElem(SqList L, int i){// ...判断i的值是否合法if(i<1||i>L.length) return false;elsereturn L.data[i-1]; //注意是i-1
}typedef struct{int *data;//指示动态分配数组的指针int MaxSize; //顺序表的最大容量int length; //顺序表的当前长度
}SeqList; 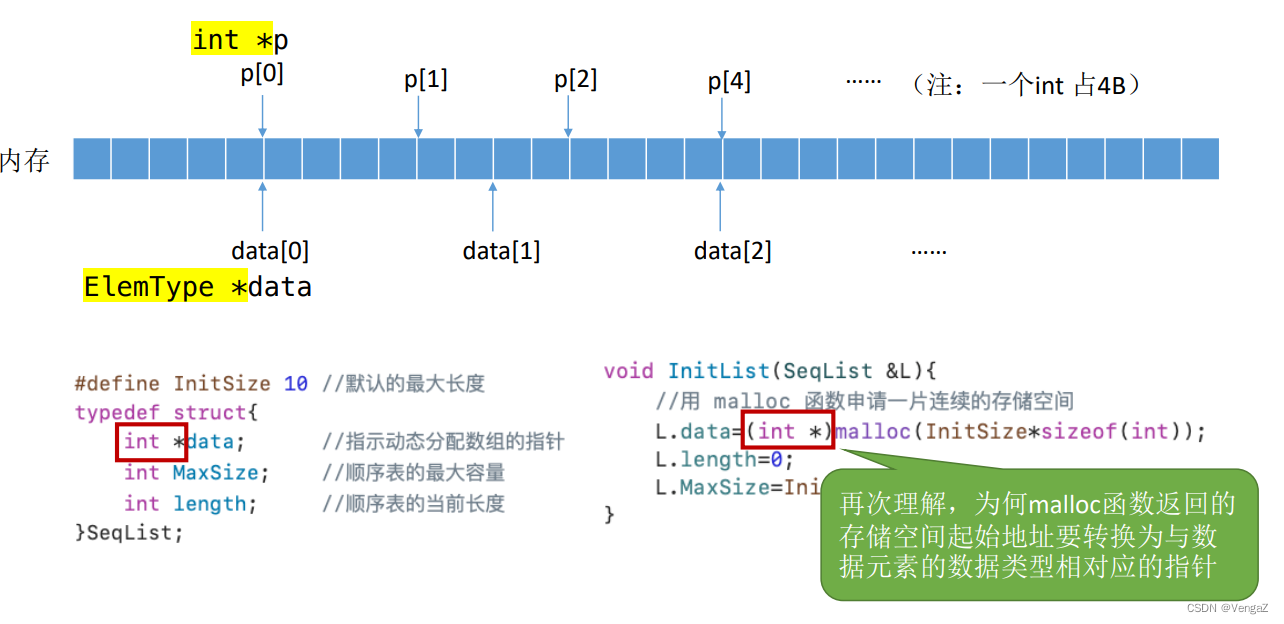
返回的指针的类型就是我们按位查找元素时指针读取的步长,倘若不对应则会报错,不能完成读取正确的数据
2.3.3.7 顺序表按位查找的时间复杂度

2.3.3.8 顺序表按值查找
#define InitSize 10 //定义最大长度
typedef struct{ElemTyp *data; //用静态的“数组”存放数据元素 int Length; //顺序表的当前长度
}SqList; //在顺序表L中查找第一个元素值等于e的元素,并返回其位序
int LocateElem(SqList L, ElemType e){for(int i=0; i<L.lengthl i++)if(L.data[i] == e) return i+1; //数组下标为i的元素值等于e,返回其位序i+1return 0; //推出循环,说明查找失败
}基本数据类型:int float double char可以用==
结构则不能使用==判断

2.3.3.9顺序表按值查找的时间复杂度

2.3.3.10 知识回顾与重要考点
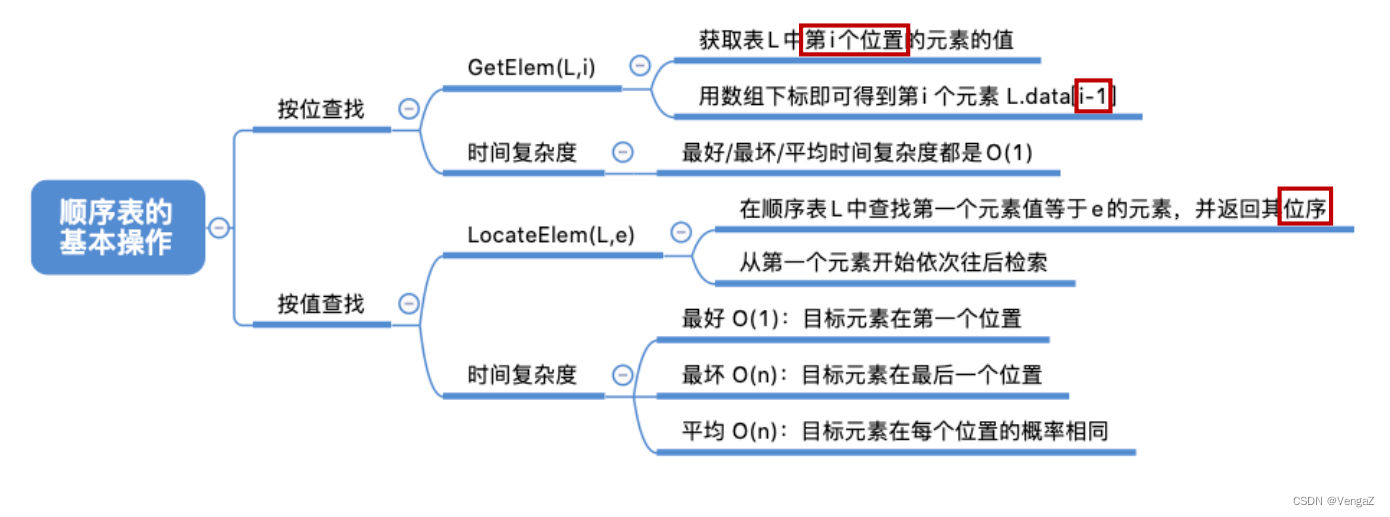
2.4 线性表的链式表示
2.4.0 引入的原因
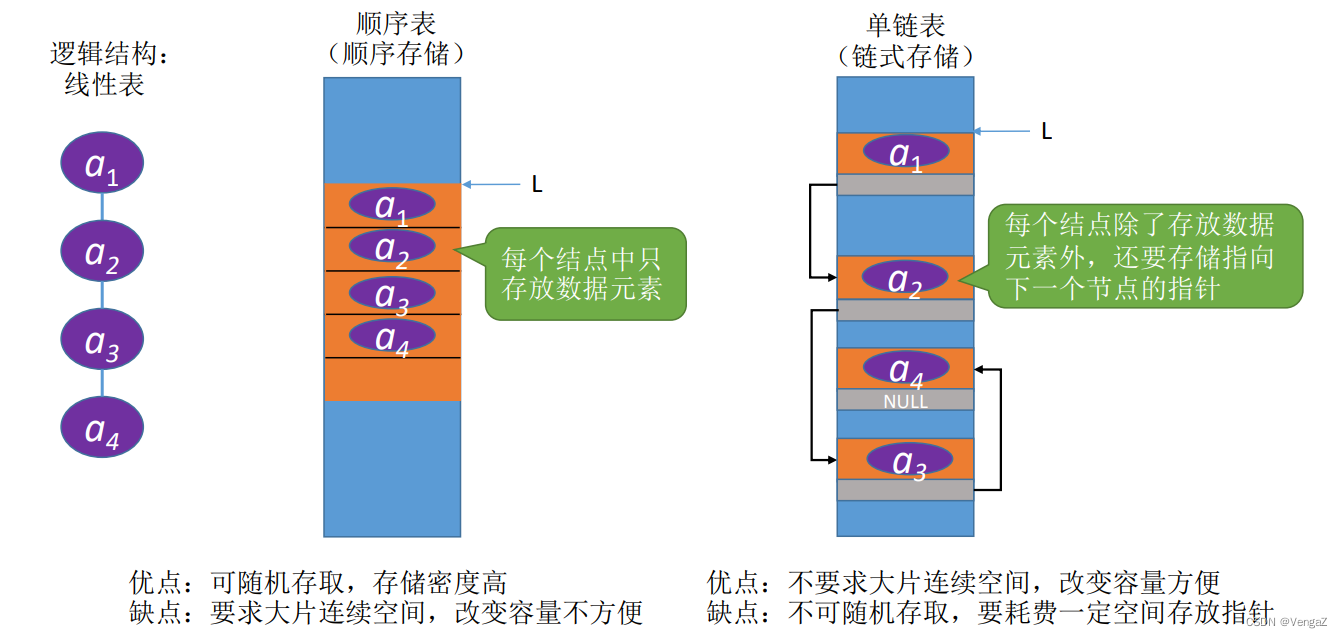
2.4.1 单链表的定义
定义: 线性表的链式存储又称单链表,它是指通过一组任意的存储单元来存储线性表中的数据元素。
typedef struct LNode{//定义单链表结点类型ElemType data; //数据域struct LNode *next;//指针域
}LNode, *LinkList;可以利用typedef关键字——数据类型重命名:type<数据类型><别名>
等价:
struct LNode{//定义单链表结点类型ElemType data; //数据域struct LNode *next;//指针域
}
typedef struct LNode LNode;
typedef struct LNode *LinkList;


2.4.2 单链表的两种实现形式
2.4.2.1 不带头结点的单链表
typedef struct LNode{ //数据结构是存有本身的数据以及下一个的地址ElemType data;struct LNode *next;
}LNode, *LinkList;//初始化一个空的单链表
bool InitList(LinkList &L){ //注意用引用 &L = NULL; //空表,暂时还没有任何结点;直接指定一个空指针当作头指针,//这个空指针指向的下一个元素就应该是有数据的第一个节点return true;
}void test(){LinkList L; //声明一个指向单链表的指针: 头指针//初始化一个空表InitList(L);//...
}//判断单链表是否为空
bool Empty(LinkList L){if (L == NULL)return true;elsereturn false;
}2.4.2.2 带头结点的单链表
头指针:开辟空间返回的指向单链表的起始物理地址的指针,仅是一个指针
不带头节点的单链表的头指针指向的头节点有数据;
带头节点的单链表的头指针指向的头节点是没有数据的
头结点:代表链表上头指针指向的第一个结点。
typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;//初始化一个单链表(带头结点)
bool InitList(LinkList &L){ L = (LNode*) malloc(sizeof(LNode)); //头指针指向的结点——分配一个头结点//(不存储数据)返回的LNode*赋值给头指针,指向的就是第一个节点头节点,头节点为空。if (L == NULL) //内存不足,分配失败return false;L -> next = NULL; //头结点之后暂时还没有结点return true;
}void test(){LinkList L; //声明一个指向单链表的指针: 头指针//初始化一个空表InitList(L);//...
}//判断单链表是否为空(带头结点)
bool Empty(LinkList L){if (L->next == NULL)return true;elsereturn false;
}2.4.2.3知识回顾与重要考点
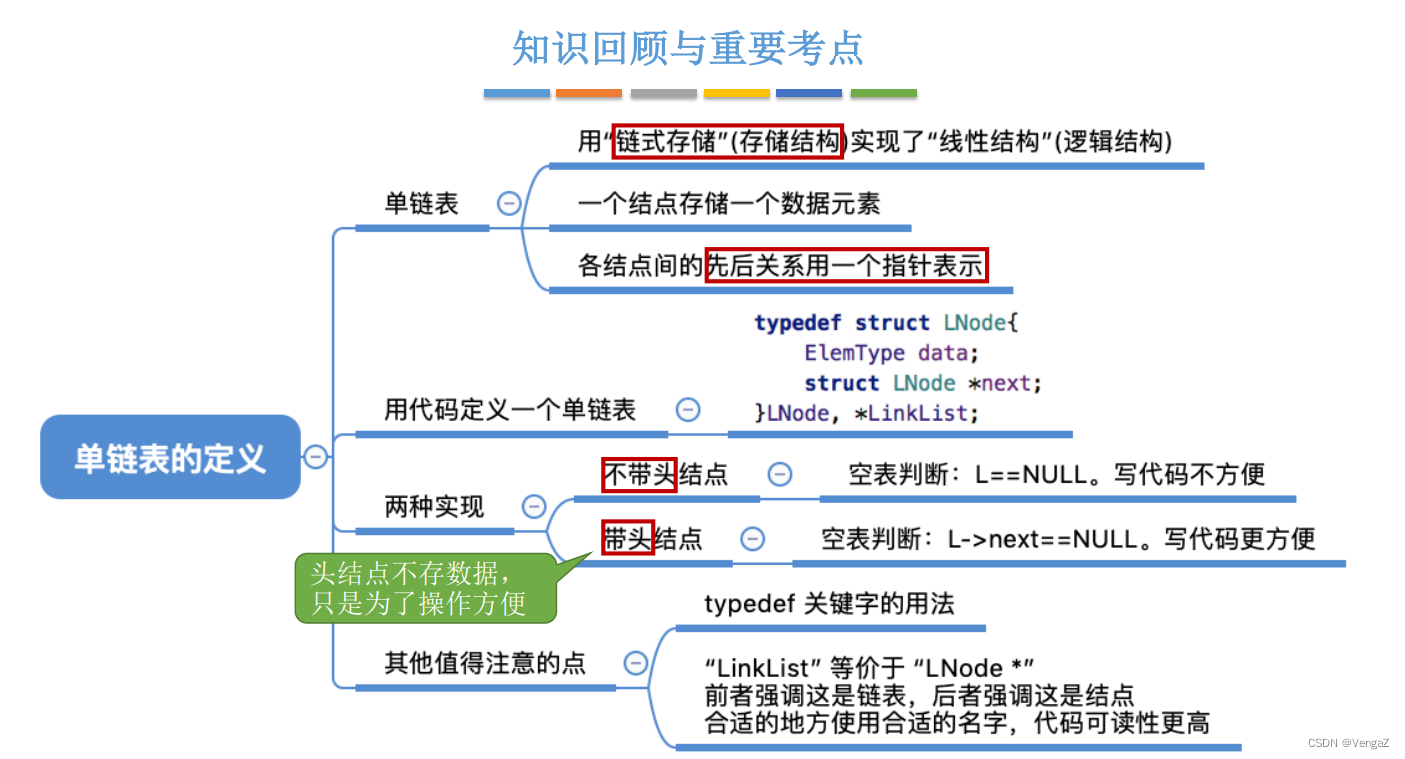
带头结点和不带头结点的比较:
不带头结点:写代码麻烦!对第一个数据节点和后续数据节点的处理需要用不同的代码逻辑,对空表和非空表的处理也需要用不同的代码逻辑; 头指针指向的结点用于存放实际数据;
带头结点:头指针指向的头结点不存放实际数据,头结点指向的下一个结点才存放实际数据;
2.4.3.1 带头结点的单链表按位序插入节点
ListInsert(&L, i, e) ;在表L中的第i个位置上插入指定元素e = 找到第i-1个结点(前驱结点),将新结点插入其后;其中头结点可以看作第0个结点,故i=1时也适用。
typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;//在第i个位置插入元素e(带头结点)
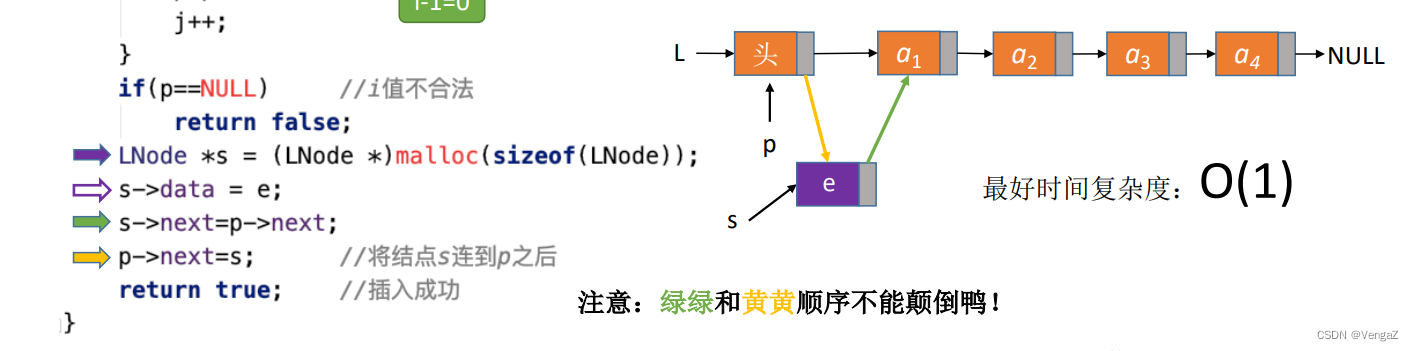
bool ListInsert(LinkList &L, int i, ElemType e){ //判断i的合法性, i是位序号(从1开始)if(i<1)return False;LNode *p; //指针p指向当前扫描到的结点 int j=0; //当前p指向的是第几个结点,=0则表示目前指向头节点,链表下标从1开始p = L; //L指向头结点,头结点是第0个结点(不存数据)//循环找到第i-1个结点,因为要修改插入节点位子的前一个节点的指针while(p!=NULL && j<i-1){ //如果i>lengh, p最后会等于NULLp = p->next; //p指向下一个结点j++;}if (p==NULL) //i值不合法return false;//在第i-1个结点后插入新结点LNode *s = (LNode *)malloc(sizeof(LNode)); //申请一个结点空间用于存放新的节点的数据s->data = e; //让新的节点的数据为es->next = p->next; //让新的节点的p->next = s; //将结点s连到p后,后两步千万不能颠倒qwqreturn true;
}- 注意:
- 1.j = 0,是头节点的位置,这个0是方便编程的,链表的下标是从1开始
- 2.需要找到的位置是i-1,因为需要修改插入节点位置的上一个LNode的指针,让它指向插入节点
- 3.倘若最后查找出来的p指针指向null,则说明i的值不合法,因为第i-1个元素已经是null了,超过了最后一个节点,指向了null
- 4.最重要的LNode的指针逻辑:首先申请一个新的LNode地址指针,指向新分配的空间;设置这个LNode的数据值为e;新分配的LNode的下一个位置指向p的下一个位置(绿色线);再将当前的p指针的下一位指向新分配的LNode(黄色线)。
- 5.倘若绿色黄色颠倒,则会产生LNode指向自己而不是原本的p指向的后边的链表,后边的链表就会丢失。
2.4.3.2 单链表的插入节点的时间复杂度
最好情况:插入表头 O(1)
最坏情况:插入表尾O(n)
平均时间复杂度:O(n)
插入每个位置(n+1个位置)的概率都是 1 n + 1 \frac{1}{n+1} n+11, ( 1 + n ) n 2 ∗ 1 n + 1 = n 2 \frac{(1+n)n}{2}*\frac{1}{n+1} =\frac{n}{2} 2(1+n)n∗n+11=2n
2.4.3.3 不带头结点的单链表的插入节点
ListInsert(&L, i, e) :在表L中的第i个位置上插入指定元素e = 找到第i-1个结点(前驱结点),将新结点插入其后; 因为不带头结点,所以不存在“第0个”结点,因此!i=1 时,需要特殊处理——插入(删除)第1个元素时,需要更改头指针L;
typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;bool ListInsert(LinkList &L, int i, ElemType e){if(i<1)return false;//插入到第1个位置时的操作有所不同!if(i==1){LNode *s = (LNode *)malloc(size of(LNode));s->data =e;s->next =L;L=s; //头指针指向新结点return true;}//i>1的情况与带头结点一样!唯一区别是j的初始值为1LNode *p; int j=1; p = L; //L指向第一个结点(存数据)//循环找到第i-1个结点while(p!=NULL && j<i-1){ //如果i>lengh, p最后会等于NULLp = p->next; //p指向下一个结点j++;}if (p==NULL) //i值不合法return false;//在第i-1个结点后插入新结点LNode *s = (LNode *)malloc(sizeof(LNode)); //申请一个结点s->data = e;s->next = p->next;p->next = s; return true;}- 注意:
- 1.最重要的LNode的i = 1的指针逻辑:首先申请一个新的LNode地址指针,指向新分配的空间;设置这个LNode的数据值为e;新分配的LNode的下一个位置指向头指针L指向的位置(s->next =L; 绿色线);再将当前的头指针L指向新分配的LNode(L=s; 黄色线)。
- 2.不带头节点插入删除i=1的节点,需要修改头指针,所以不带头指针需要考虑对i=1操作的情况会比较麻烦。
- 3.此时对于定位的j,需要设置初始值为1,而不是带头节点的0。
- 4.若i不为1,则操作都一样
2.4.3.4 不带头结点的单链表的插入节点的时间复杂度
同上
最好情况:插入表头 O(1)
最坏情况:插入表尾O(n)
平均时间复杂度:O(n)
插入每个位置(n+1个位置)的概率都是 1 n + 1 \frac{1}{n+1} n+11, ( 1 + n ) n 2 ∗ 1 n + 1 = n 2 \frac{(1+n)n}{2}*\frac{1}{n+1} =\frac{n}{2} 2(1+n)n∗n+11=2n
2.4.3.5 指定节点的后插操作
InsertNextNode(LNode *p, ElemType e): 给定一个结点p,在其之后插入元素e; 根据单链表的链接指针只能往后查找,故给定一个结点p,那么p之后的结点我们都可知,但是p结点之前的结点无法得知;
typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;bool InsertNextNode(LNode *p, ElemType e){if(p==NULL){return false;}LNode *s = (LNode *)malloc(sizeof(LNode));//某些情况下分配失败,比如内存不足if(s==NULL)return false;s->data = e; //用结点s保存数据元素e s->next = p->next;p->next = s; //将结点s连到p之后return true;
} //平均时间复杂度 = O(1)//有了后插操作,那么在第i个位置上插入指定元素e的代码可以改成:
bool ListInsert(LinkList &L, int i, ElemType e){ if(i<1)return False;LNode *p; //指针p指向当前扫描到的结点 int j=0; //当前p指向的是第几个结点p = L; //L指向头结点,头结点是第0个结点(不存数据)//循环找到第i-1个结点while(p!=NULL && j<i-1){ //如果i>lengh, p最后4鸟会等于NULLp = p->next; //p指向下一个结点j++;}return InsertNextNode(p, e)
}- 注意:
- 1.bool InsertNextNode(LNode *p, ElemType e),后插操作判断给的指针是否是空指针;判断是否内存分配失败
- 2.找到第i-1个节点就可以调用这个后插函数 return InsertNextNode(p, e)
- 3.时间复杂度为O(1)
if(p==NULL){return false;}LNode *s = (LNode *)malloc(sizeof(LNode));//某些情况下分配失败,比如内存不足if(s==NULL)return false;
2.4.3.6 指定节点的前插操作
InsertPriorNode(LNode *p, ElenType e) 思想:设待插入结点是s,将s插入到p的前面。我们仍然可以将s插入到*p的后面。然后将p->data与s->data交换,这样既能满足了逻辑关系,又能是的时间复杂度为O(1).
-
传入头指针,从头开始遍历寻找到指定节点前驱
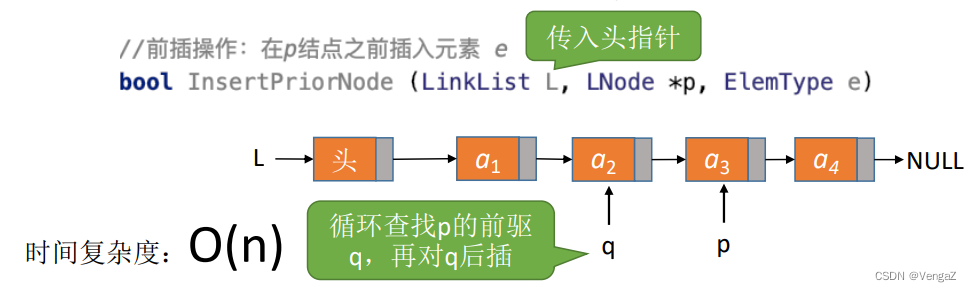
-
不传入头节点,使用交换指定节点和需要插入节点的数据,完成操作
该方法时间复杂度为O(1)
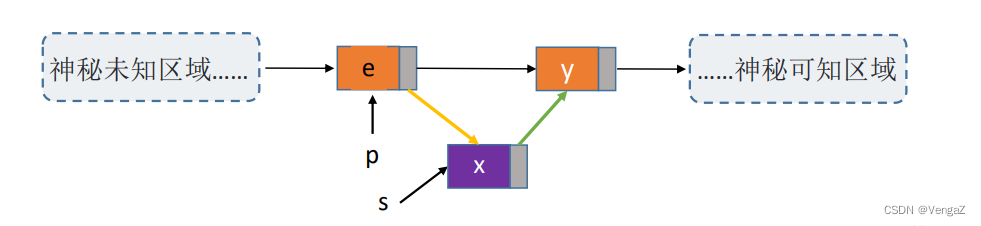
//前插操作:在p结点之前插入元素e
bool InsertPriorNode(LNode *p, ElenType e){if(p==NULL)return false;LNode *s = (LNode *)malloc(sizeof(LNode));if(s==NULL) //内存分配失败return false;//重点来了!s->next = p->next;p->next = s; //新结点s连到p之后s->data = p->data; //将p中元素复制到sp->data = e; //p中元素覆盖为ereturn true;
} //时间复杂度为O(1)- 王道书上版本(传入指定节点与需要插入的节点)
bool InsertPriorNode(LNode *p, LNode *s){if(p==NULL || S==NULL)return false;s->next = p->next;p->next = s; ///s连接到pELemType temp = p->data; //声明临时变量temp存储p的数据p->data = s->data; //用需要插入节点的数据覆盖p中的数据s->data = temp; //将临时变量赋值给s的数据部分return true;
}ELemType temp = p->data; //交换数据域部分,声明临时变量temp存储p的数据
2.4.3.7 按位序删除节点(带头结点)
ListDelete(&L, i, &e) : 删除操作,删除表L中第i个位置的元素,并用e返回删除元素的值;头结点视为“第0个”结点;
思路:找到第i-1个结点,将其指针指向第i+1个结点,并释放第i个结点;
typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;bool ListDelete(LinkList &L, int i, ElenType &e){if(i<1) return false;LNode *p; //指针p指向当前扫描到的结点 int j=0; //当前p指向的是第几个结点p = L; //L指向头结点,头结点是第0个结点(不存数据)//循环找到第i-1个结点while(p!=NULL && j<i-1){ //如果i>lengh, p最后会等于NULLp = p->next; //p指向下一个结点j++;}if(p==NULL) return false;if(p->next == NULL) //第i-1个结点之后已无其他结点return false;LNode *q = p->next; //令q指向被删除的结点e = q->data; //用e返回被删除元素的值p->next = q->next; //将*q结点从链中“断开”free(q) //释放结点的存储空间return true;
}2.4.3.8 按位序删除节点(带头结点)的时间复杂度
同上
最好情况:插入表头 O(1)
最坏情况:插入表尾O(n)
平均时间复杂度:O(n)
2.4.3.9 指定结点的删除
bool DeleteNode(LNode *p){if(p==NULL)return false;LNode *q = p->next; //令q指向*p的后继结点p->data = p->next->data; //让p和后继结点交换数据域p->next = q->next; //将*q结点从链中“断开”free(q);return true;
} //时间复杂度 = O(1)倘若需要删除的是最后一个节点,则时间复杂度为O(n),因为找不到下一个节点不能跟它交换数据,再free它。只能从链表的头开始寻找到该指针的前继节点,将它指向null。
2.4.3.10 知识回顾与重要考点
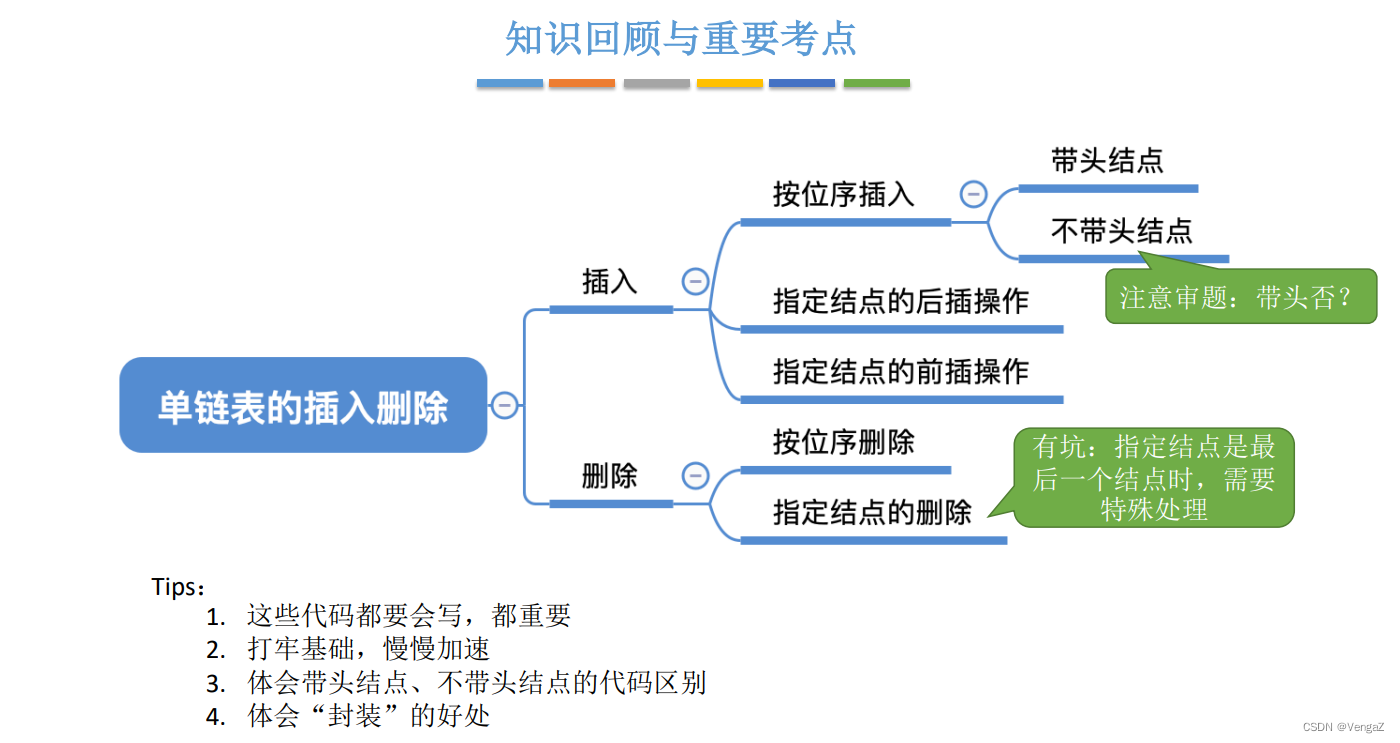
2.4.4单链表的查找操作(默认带头节点,不带头节点后续更新)
2.4.4.1 按位查找操作
GetElem(L, i): 按位查找操作,获取表L中第i个位置的元素的值;
LNode * GetElem(LinkList L, int i){if(i<0) return NULL;LNode *p; //指针p指向当前扫描到的结点int j=0; //当前p指向的是第几个结点p = L; //L指向头结点,头结点是第0个结点(不存数据)while(p!=NULL && j<i){ //循环找到第i个结点p = p->next;j++;}return p; //返回p指针指向的值
}- 注意:
- 1.边界情况 i=0,返回头节点;i>L.length,返回null;
- 2.j<i即查找到j = i 的节点,就是第i个节点。
- 3.平均复杂度O(n)
2.4.4.2 按值查找操作
LocateElem(L, e):按值查找操作,在表L中查找具有给定关键字值的元素;
平均复杂度O(n)
LNode * LocateElem(LinkList L, ElemType e){LNode *P = L->next; //p指向第一个结点//从第一个结点开始查找数据域为e的结点while(p!=NULL && p->data != e){p = p->next;}return p; //找到后返回该结点指针,否则返回NULL
}2.4.4.3 求单链表的长度(带和不带头节点都写了)
Length(LinkList L) :计算单链表中数据结点**(不含头结点)的个数**,需要从第一个结点看是顺序依次访问表中的每个结点。算法的时间复杂度为O(n)。
带头节点:
int Length(LinkList L){int len=0; //统计表长LNode *p = L;while(p->next != NULL){ //只有指向的下一个节点不为null,才len++p = p->next;len++;}return len;
}不带头节点:
int Length(LinkList L){int len=0; //统计表长LNode *p = L;while(p!= NULL){ //当前指针(即头节点指向的第一个节点)不为空即可++,//带头节点的链表用这种方法长度会算上头节点。p = p->next;len++;}return len;
}2.4.4.4 知识回顾与重要考点
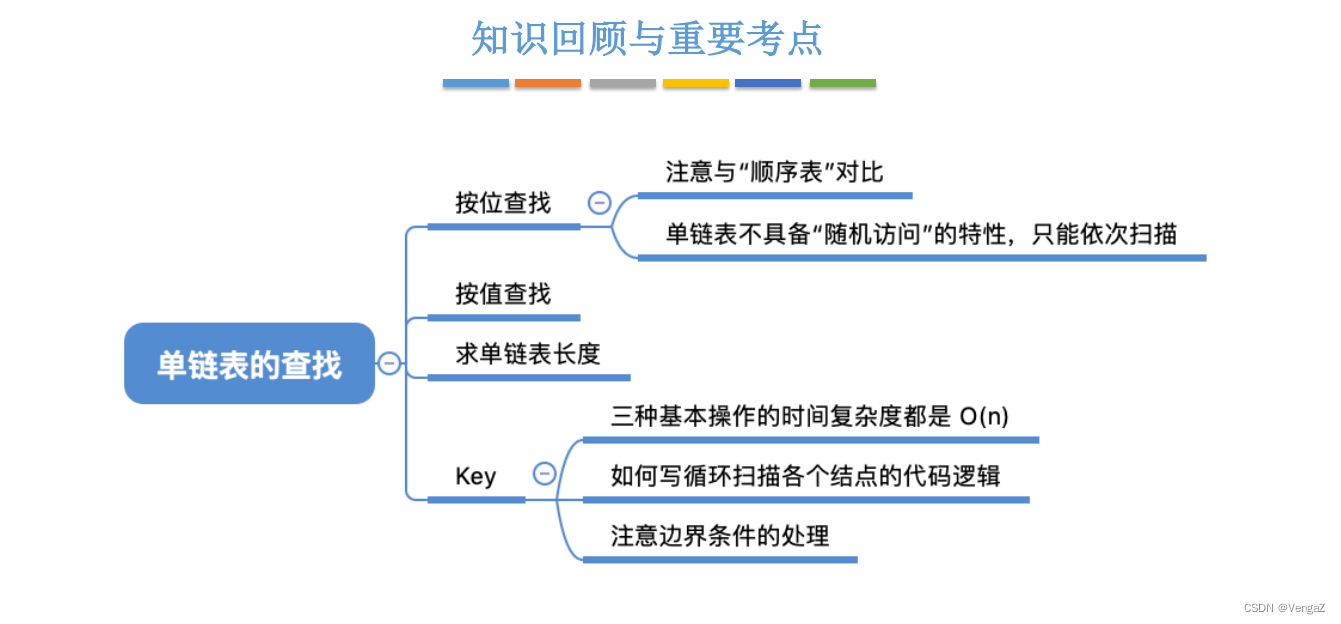
2.4.5 单链表的创建操作
2.4.5.1 头插法建立单链表
带头节点;
若不带头节点,头插法就是插入头指针指向的第一个节点
平均时间复杂度O(n)
思路:每次都将生成的结点插入到链表的表头。
LinkList List_HeadInsert(LinkList &L){ //逆向建立单链表LNode *s;int x;L = (LinkList)malloc(sizeof(LNode)); //建立头结点L->next = NULL; //初始为空链表,这步不能少!scanf("%d", &x); //输入要插入的结点的值while(x!=9999){ //输入9999表结束s = (LNode *)malloc(sizeof(LNode)); //创建新结点s->data = x;s->next = L->next;L->next = s; //将新结点插入表中,L为头指针scanf("%d", &x); }return L;}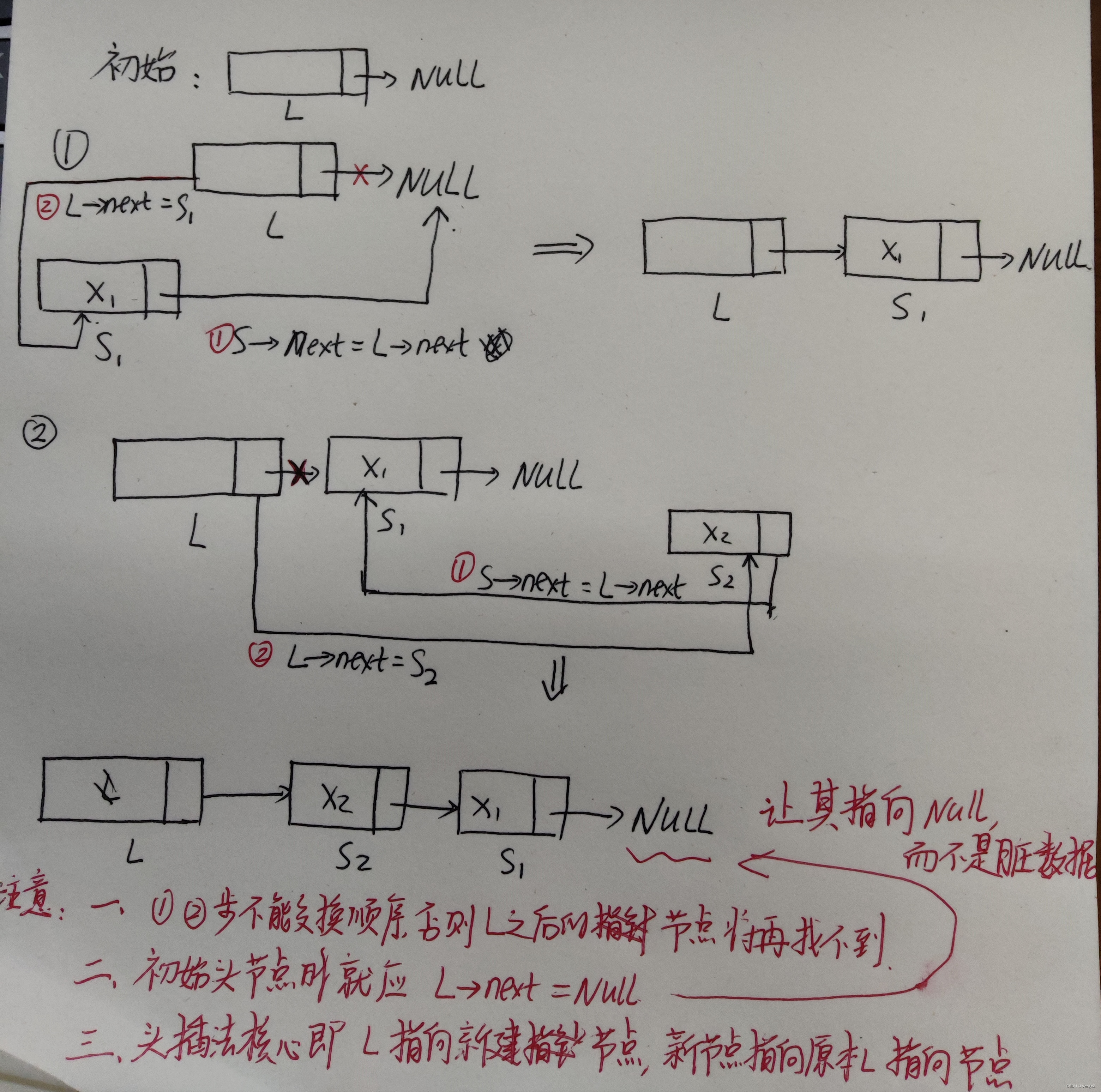
2.4.5.2 尾插法建立单链表
带头节点;
若不带头节点则需要特殊处理第一次插入数据的情况,是直接赋值而不是对下一个节点赋值。
时间复杂度O(n)
思路:每次将新节点插入到当前链表的表尾,所以必须增加一个尾指针r,使其始终指向当前链表的尾结点。
好处:生成的链表中结点的次序和输入数据的顺序会一致。
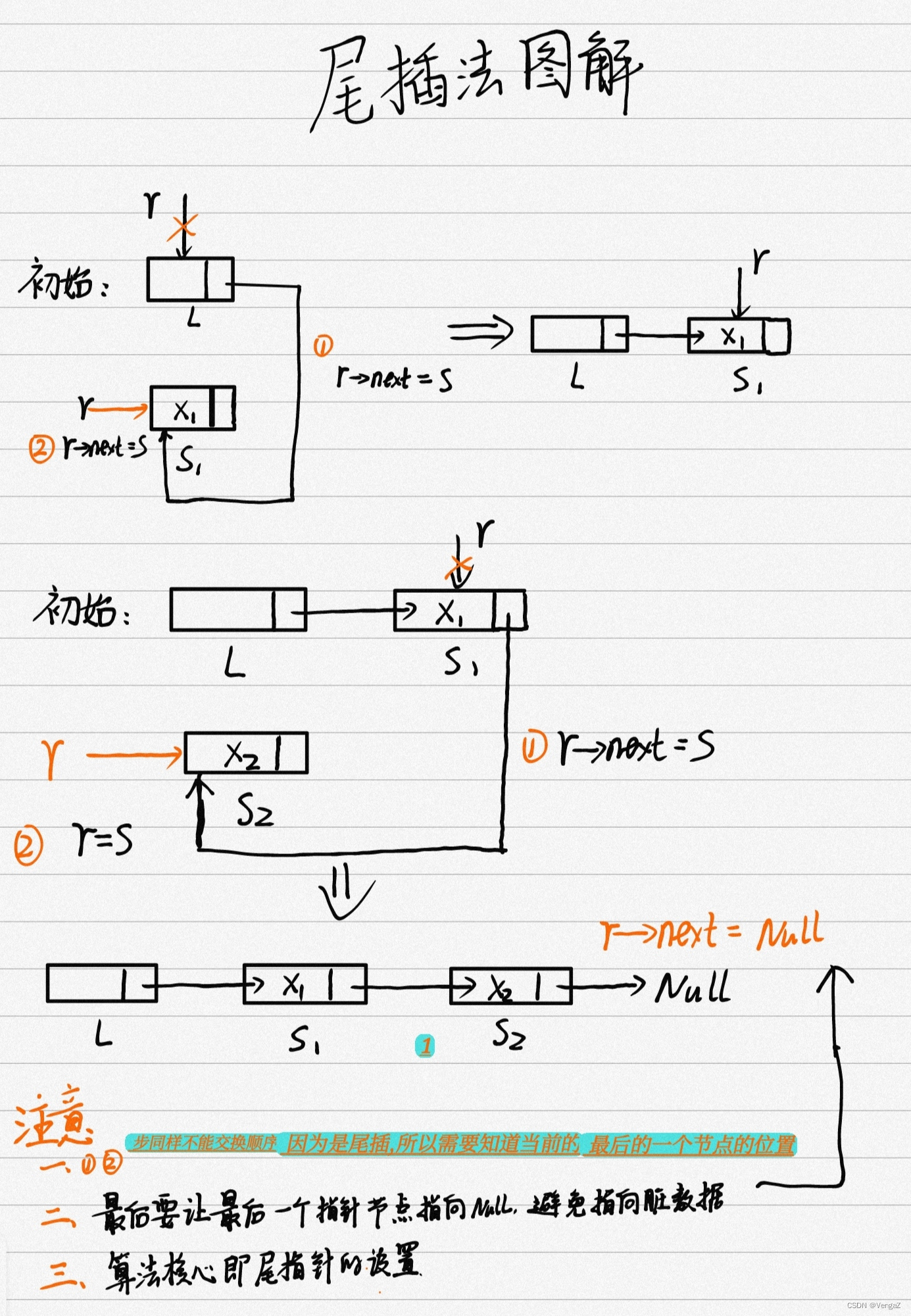
LinkList List_TailInsert(LinkList &L){ //正向建立单链表int x; //设ElemType为整型intL = (LinkList)malloc(sizeof(LNode)); //建立头结点(初始化空表)LNode *s, *r = L; //r为表尾指针scanf("%d", &x); //输入要插入的结点的值while(x!=9999){ //输入9999表结束s = (LNode *)malloc(sizeof(LNode));s->data = x;r->next = s;r = s //r指针指向新的表尾结点scanf("%d", &x); }r->next = NULL; //尾结点指针置空return L;
}
- 注意:
- 头插法和尾插法在初始化的时候
头插法:L = (LinkList)malloc(sizeof(LNode)); //建立头结点L->next = NULL; //初始为空链表,这步不能少!
尾插法:L = (LinkList)malloc(sizeof(LNode)); //建立头结点(初始化空表)r->next = NULL; //尾结点指针置空
都是为了保证最后一个节点指向的不是脏数据,即malloc动态分配空间的时候可能,
指向的是一个脏数据
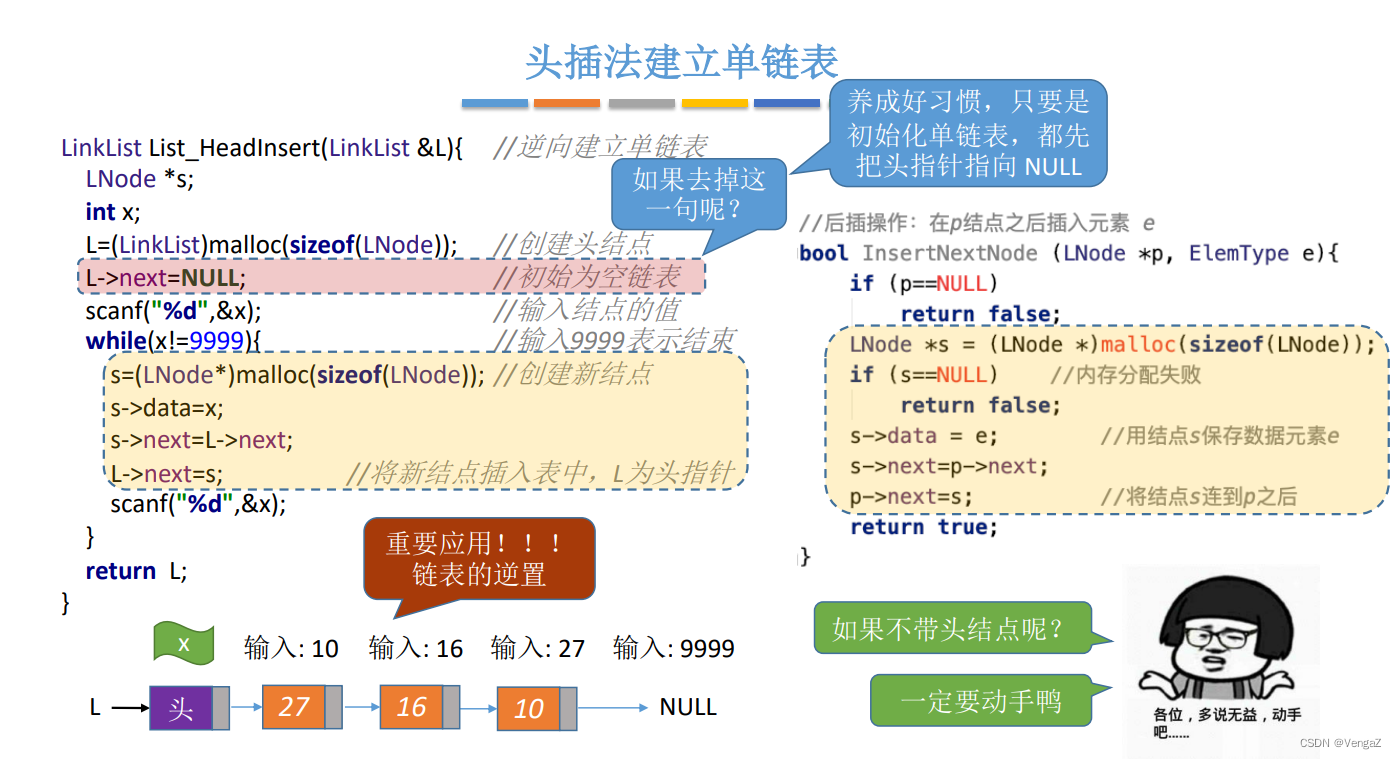
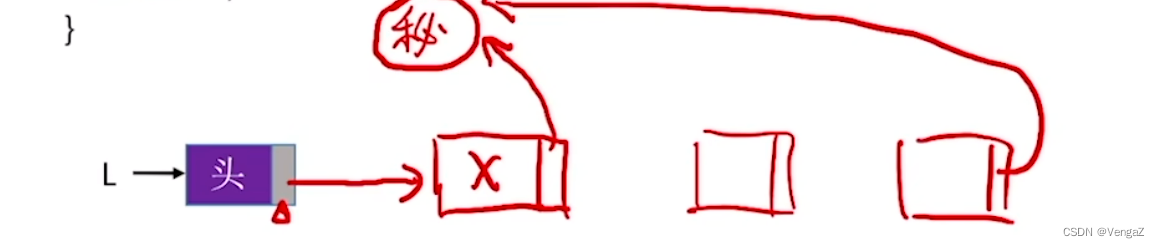
2.4.5.3 链表的逆置
算法思想:逆置链表初始为空,原表中结点从原链表中依次“删除”,再逐个插入逆置链表的表头(即“头插”到逆置链表中),使它成为逆置链表的“新”的第一个结点,如此循环,直至原链表为空;
带头节点:
void listReverse(linkedList &L)
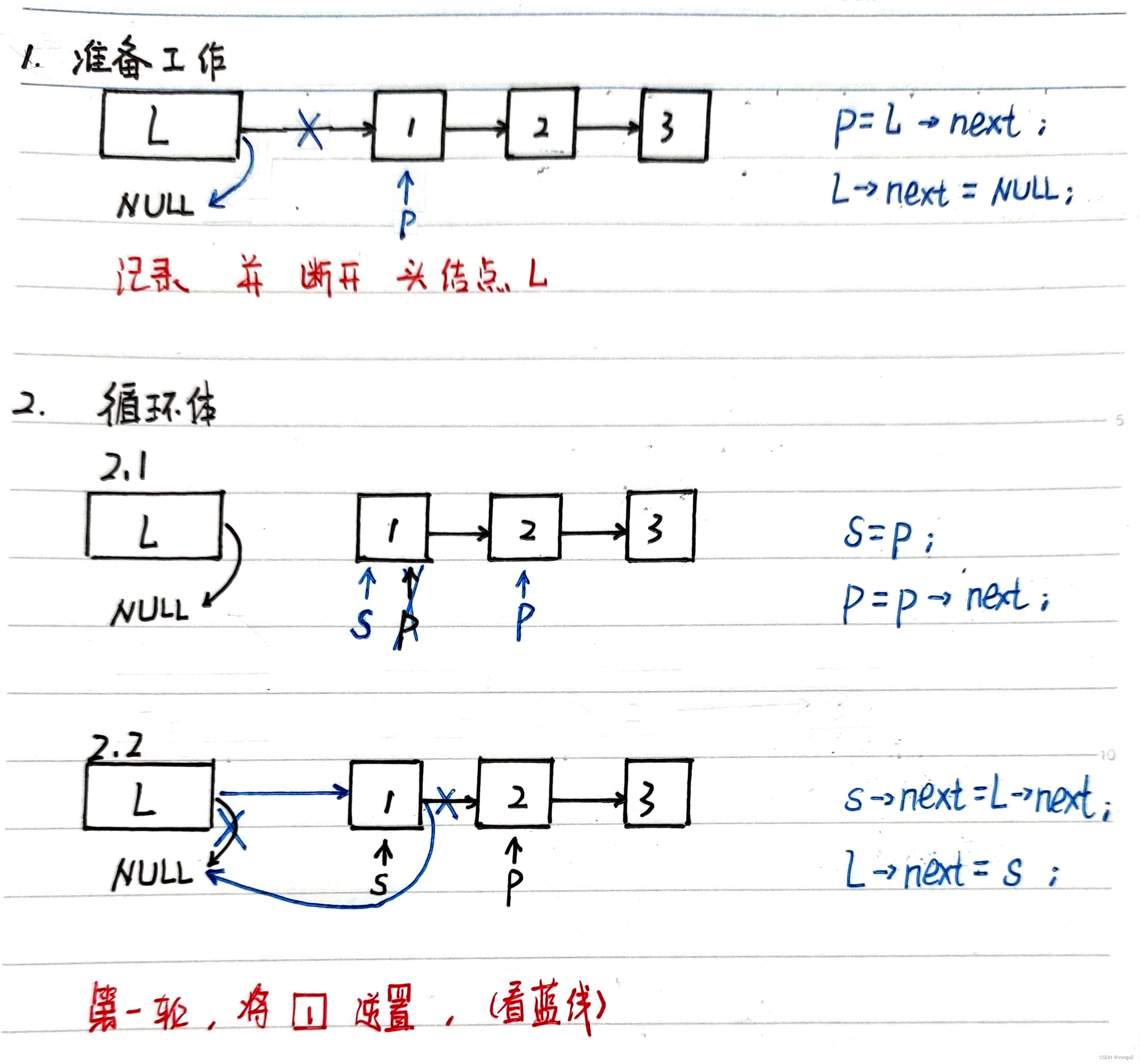
{node *p,*s;//1.准备工作p = L->next;L->next = NULL;while(p){//2.1 s记录正在处理的结点,p记录下一轮待处理的结点s = p; //s承接上一轮记录的位置p = p->next; //p为下一轮记录位置//2.2 把s插入 已逆置的部分 中s->next = L->next; // L->next代表已逆置的第一结点,s的指针域指向它L->next = s; //(头结点的指针域,即)第一结点 设置为s//2.2步骤相当于://s 对 队伍(已逆置部分)的队首(已逆置的第一结点)说:你不要排在柜台前了,你排在我后面//等队伍排在s后面后,s自己排到了柜台前}
}讲解
我们先看第一轮循环做了什么:
阅读顺序:黑色(初始)、蓝色(操作)、红色(理解)
第二轮:
阅读顺序:黑色(初始)、蓝色(操作)、红色(理解)
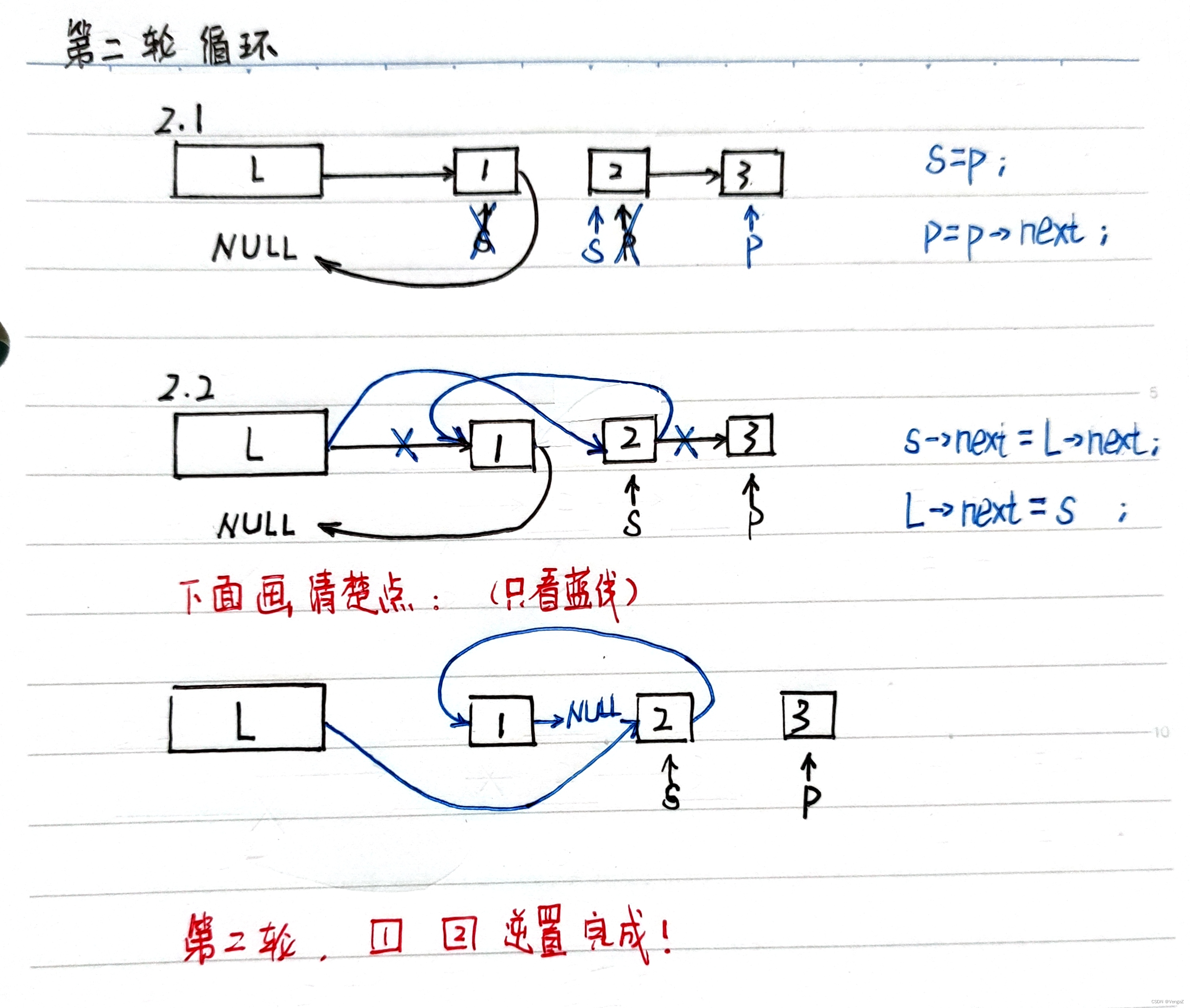
总结
不难发现:
-
链表逆置利用了s、p两个指针的移动实现
每一轮循环体执行结束后,s指向刚刚逆置成功的结点,p指向下一轮待逆置的结点 -
为什么需要p?
因为2.2步骤中s->next会被改写,
若只有s,会丢失剩余的结点,
这时候p起到暂存的作用,等待下一轮2.1步骤中的s=p找到它。
2.4.6 双链表
2.4.6.1 双链表中节点类型的描述:
typedef struct DNode{ //定义双链表结点类型ElemType data; //数据域struct DNode *prior, *next; //前驱和后继指针
}DNode, *DLinklist;存储密度更低,因为需要额外空间存储前驱指针
2.4.6.2 双链表的初始化
typedef struct DNode{ //定义双链表结点类型ElemType data; //数据域struct DNode *prior, *next; //前驱和后继指针
}DNode, *DLinklist;//初始化双链表
bool InitDLinkList(Dlinklist &L){L = (DNode *)malloc(sizeof(DNode)); //分配一个头结点if(L==NULL) //内存不足,分配失败return false;L->prior = NULL; //头结点的prior指针永远指向NULLL->next = NULL; //头结点之后暂时还没有结点return true;
}void testDLinkList(){//初始化双链表DLinklist L; // 定义指向头结点的指针LInitDLinkList(L); //申请一片空间用于存放头结点,指针L指向这个头结点//...
}//判断双链表是否为空
bool Empty(DLinklist L){if(L->next == NULL) //判断头结点的next指针是否为空return true;elsereturn false;
}2.4.6.3 双链表的插入操作
- 后插操作
InsertNextDNode(p, s): 在p结点后插入s结点 - 按位序插入操作:
思路:从头结点开始,找到某个位序的前驱结点,对该前驱结点执行后插操作; - 前插操作:
思路:找到给定结点的前驱结点,再对该前驱结点执行后插操作;
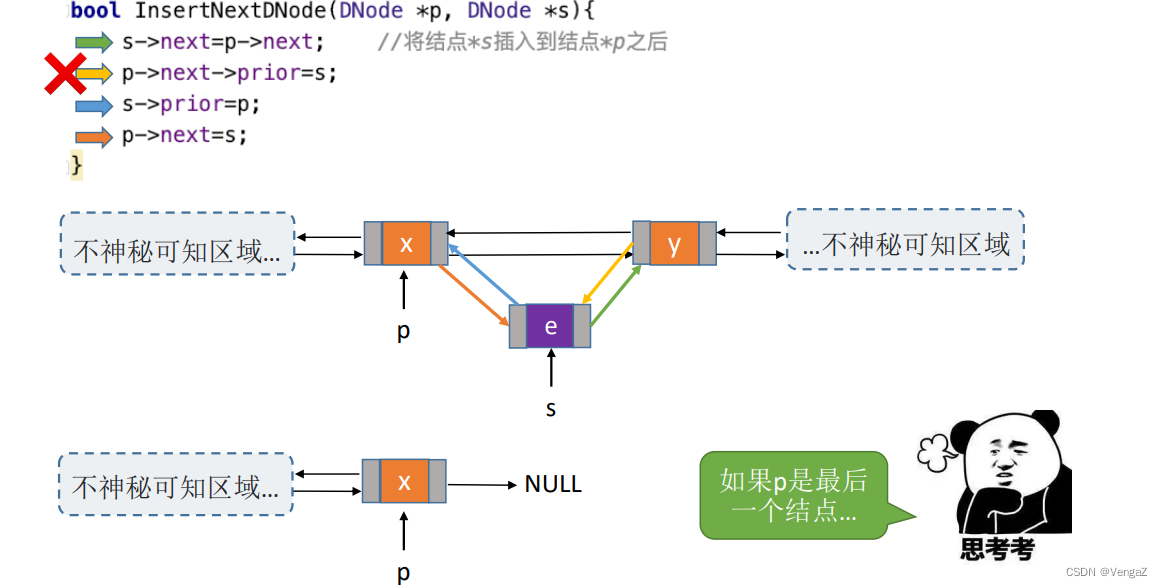
bool InsertNextDNode(DNode *p, DNode *s){ //将结点 *s 插入到结点 *p之后if(p==NULL || s==NULL) //非法参数return false;s->next = p->next; //1if (p->next != NULL) //p不是最后一个结点=p有后继结点 p->next->prior = s; //2s->prior = p; //3p->next = s; //4return true;
}
2.4.6.4 双链表的删除操作
删除p节点的后继节点 (遍历实现)
//删除p结点的后继结点
bool DeletNextDNode(DNode *p){if(p==NULL) return false;DNode *q =p->next; //找到p的后继结点qif(q==NULL) return false; //p没有后继结点;p->next = q->next;if(q->next != NULL) //q结点不是最后一个结点q->next->prior=p;free(q);return true;
}//销毁一个双链表
bool DestoryList(DLinklist &L){//循环释放各个数据结点while(L->next != NULL){DeletNextDNode(L); //删除头结点的后继结点free(L); //释放头结点L=NULL; //头指针指向NULL}
}2.4.6.5 双链表的遍历操作
前向遍历
while(p!=NULL){//对结点p做相应处理,eg打印p = p->prior;
}后向遍历
while(p!=NULL){//对结点p做相应处理,eg打印p = p->next;
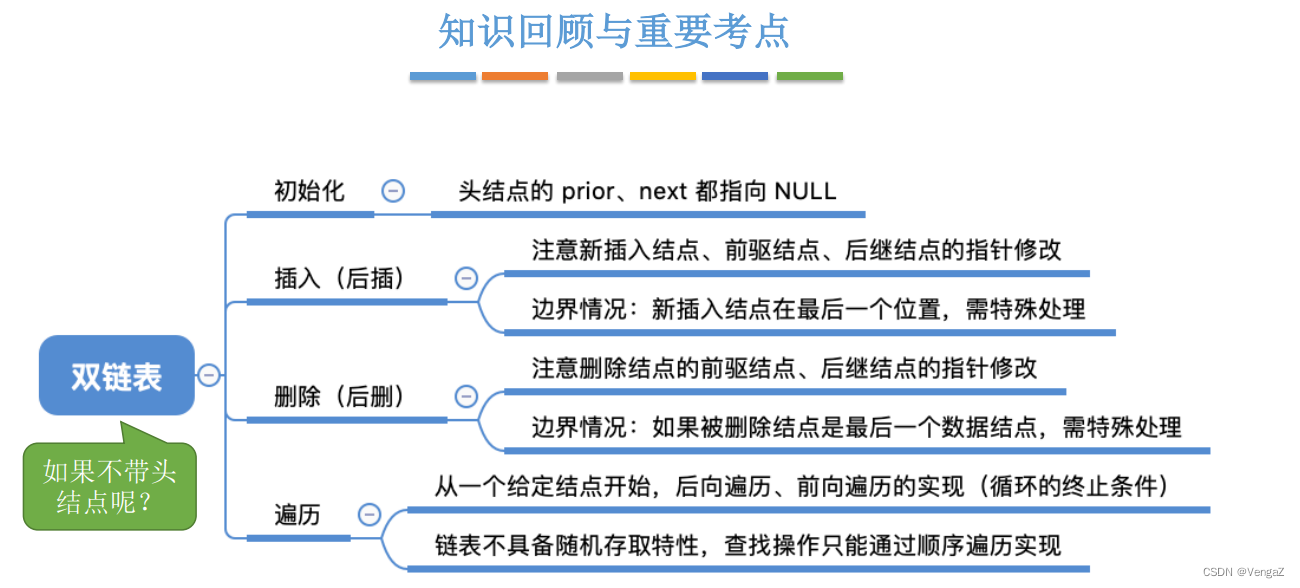
}2.4.6.6 知识回顾与重要考点
2.4.7 循环链表
2.4.7.1 循环单链表
最后一个结点的指针不是NULL,而是指向头结点
L->next = L; //头结点next指针指向头结点L->next == L ; //判空
p->next == L ; //判断是否是尾节点
typedef struct LNode{ ElemType data; struct LNode *next;
}DNode, *Linklist;/初始化一个循环单链表
bool InitList(LinkList &L){L = (LNode *)malloc(sizeof(LNode)); //分配一个头结点if(L==NULL) //内存不足,分配失败return false;L->next = L; //头结点next指针指向头结点return true;
}//判断循环单链表是否为空(终止条件为p或p->next是否等于头指针)
bool Empty(LinkList L){if(L->next == L)return true; //为空elsereturn false;
}//判断结点p是否为循环单链表的表尾结点
bool isTail(LinkList L, LNode *p){if(p->next == L)return true;elsereturn false;
}2.4.7.2 单链表和循环单链表的比较:
单链表:从一个结点出发只能找到该结点后续的各个结点;对链表的操作大多都在头部或者尾部;设立头指针,从头结点找到尾部的时间复杂度O(n),即对表尾进行操作需要O(n)的时间复杂度;
循环单链表:从一个结点出发,可以找到其他任何一个结点;设立尾指针,从尾部找到头部的时间复杂度为O(1),即对表头和表尾进行操作都只需要O(1)的时间复杂度;
优点:从表中任一节点出发均可找到表中其他结点。
2.4.7.3 循环双链表
表头结点的prior指向表尾结点,表尾结点的next指向头结点
L->prior = L; //头结点的prior指向头结点
L->next = L; //头结点的next指向头结点L->next == L //判空
p->next == L //判断是否为表尾
typedef struct DNode{ ElemType data; struct DNode *prior, *next;
}DNode, *DLinklist;//初始化空的循环双链表
bool InitDLinkList(DLinklist &L){L = (DNode *) malloc(sizeof(DNode)); //分配一个头结点if(L==NULL) //内存不足,分配失败return false; L->prior = L; //头结点的prior指向头结点L->next = L; //头结点的next指向头结点
}void testDLinkList(){//初始化循环单链表DLinklist L;InitDLinkList(L);//...
}//判断循环双链表是否为空
bool Empty(DLinklist L){if(L->next == L)return true;elsereturn false;
}//判断结点p是否为循环双链表的表尾结点
bool isTail(DLinklist L, DNode *p){if(p->next == L)return true;elsereturn false;
}双链表的插入(循环双链表):
不同于双链表的的操作,循环双链表的插入操作不需要判断 p->next->prior = s;这一步的 p->next->prior 是否存在,即p的下一个节点是不是null。
bool InsertNextDNode(DNode *p, DNode *s){ s->next = p->next;p->next->prior = s;s->prior = p;p->next = s;
双链表的删除
同理 q->next->prior
//删除p的后继结点q
p->next = q->next;
q->next->prior = p;
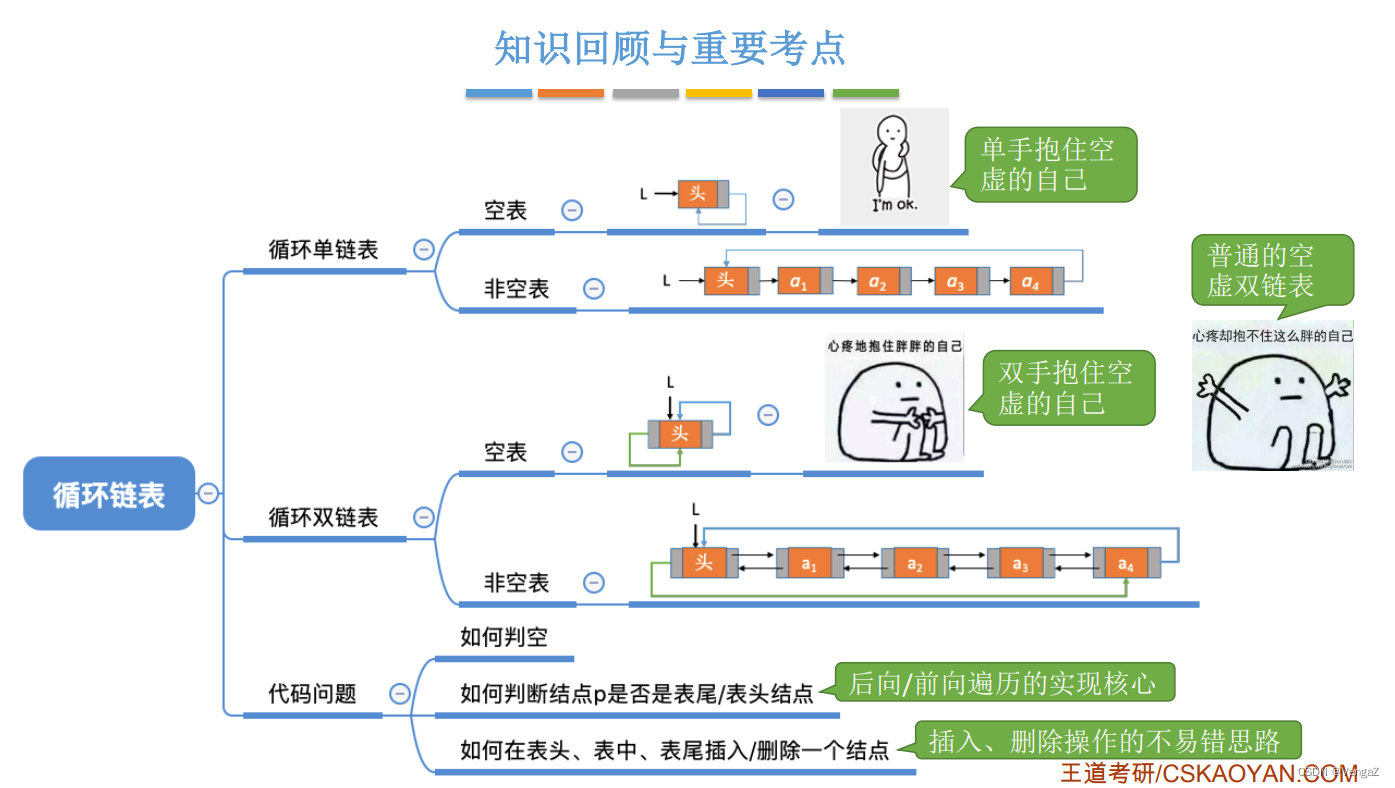
free(q);2.4.7.4 知识回顾与重要考点
2.4.8 静态链表
- 定义:
单链表:各个结点散落在内存中的各个角落,每个结点有指向下一个节点的指针(下一个结点在内存中的地址);
静态链表:用数组的方式来描述线性表的链式存储结构: 分配一整片连续的内存空间,各个结点集中安置,包括了——数据元素and下一个结点的数组下标(游标)
其中数组下标为0的结点充当"头结点"
游标为-1表示已经到达表尾
游标为-2表示该位置为空,没有数据且没有游标指向这个位置
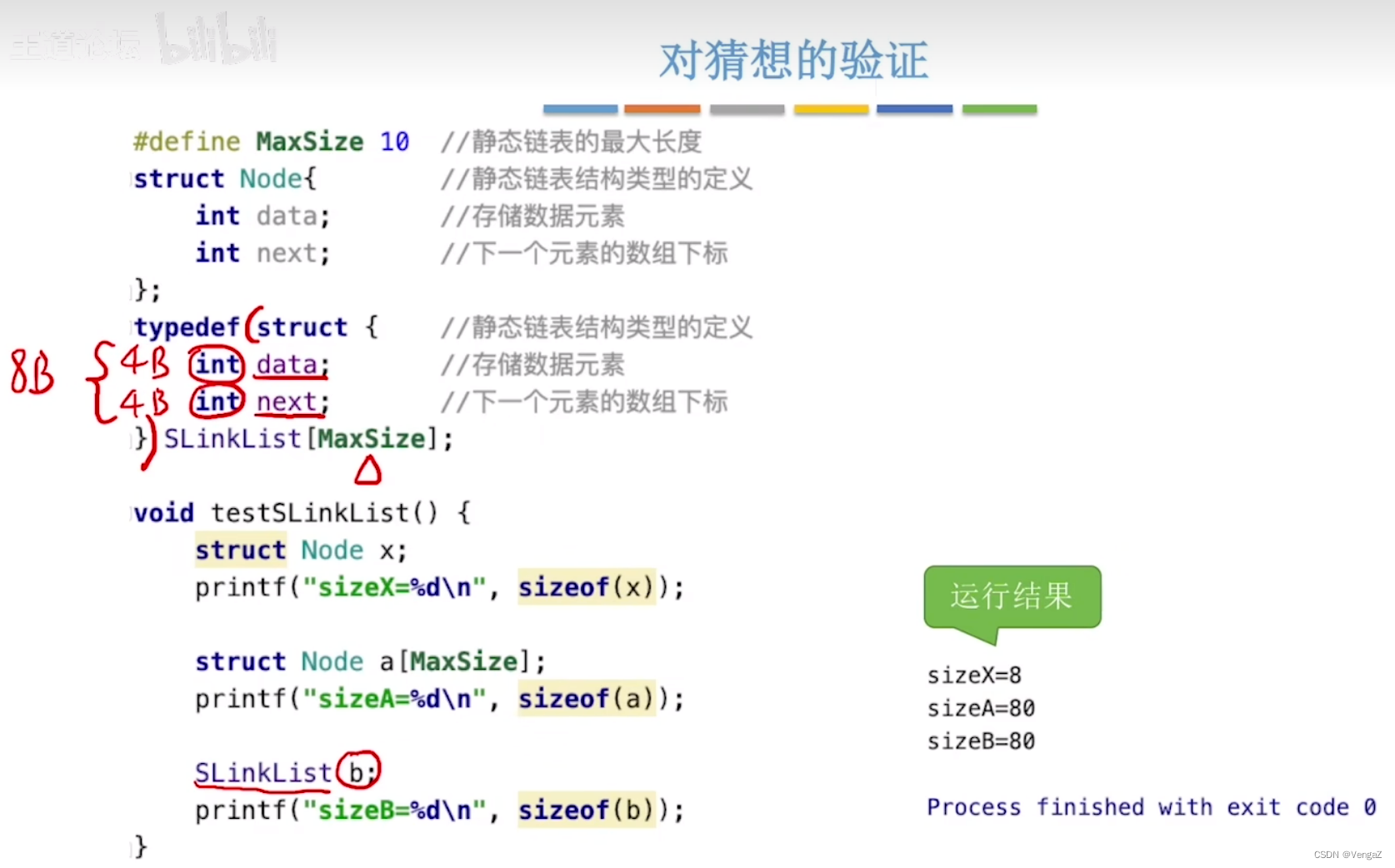
若每个数据元素为4B,每个游标为4B,则每个结点共8B;假设起始地址为addr,则数据下标为2的存放地址为:addr+8*2
注意: 数组下标——物理顺序,位序——逻辑顺序;
优点:增、删操作不需要大量移动元素;
缺点:不能随机存取,只能从头结点开始依次往后查找,容量固定不变!
-
几种写法:
注意:SLinkList a 强调a是静态链表;struct Node a 强调a是一个Node型数组;
-
静态链表基本操作的实现
-
初始化静态链表:把a[0]的next设为-1
-
查找某个位序(不是数组下标,位序是各个结点在逻辑上的顺序)的结点:从头结点出发挨个往后遍历结点,时间复杂度O=(n)
-
在位序为i上插入结点:① 找到一个空的结点,存入数据元素;② 从头结点出发找到位序为i-1的结点;③修改新结点的next;④ 修改i-1号结点的next;
-
删除某个结点:① 从头结点出发找到前驱结点;② 修改前驱节点的游标;③ 被删除节点next设为-2;
2.4.9 顺序表和链表的比较
2.4.9.1 逻辑结构
- 顺序表和链表都属于线性表,都是线性结构
2.4.9.2 存储结构
-
顺序表:顺序存储
优点:支持随机存取,存储密度高
缺点:大片连续空间分配不方便,改变容量不方便 -
链表:链式存储
优点:离散的小空间分配方便,改变容量方便
缺点:不可随机存取,存储密度低
2.4.9.3 基本操作 - 创建
-
顺序表:需要预分配大片连续空间。若分配空间过小,则之后不方便拓展容量;若分配空间过大,则浪费内存资源;
-
静态分配:静态数组,容量不可改变
-
动态分配:动态数组,容量可以改变,但是需要移动大量元素,时间代价高(malloc(),free())
-
链表:只需要分配一个头结点或者只声明一个头指针
2.4.9.4 基本操作 - 销毁
顺序表:
首先修改 Length = 0
- 静态数组——系统自动回收空间
typedef struct{ElemType *data;int MaxSize;int length;
}SeqList;
创建的时候静态建立没有malloc分配空间。
- 动态分配:动态数组——需要手动free(),一个malloc对应一个free,成对出现
//创
L.data = (ELemType *)malloc(sizeof(ElemType) *InitSize)
//销
free(L.data);//!malloc() 和 free() 必须成对出现2.4.9.5 基本操作-增/删
-
顺序表:插入/删除元素要将后续元素后移/前移;时间复杂度=O(n),时间开销主要来自于移动元素;
-
链表:插入/删除元素只需要修改指针;时间复杂度=O(n),时间开销主要来自查找目标元素
需要注意的是:在单个元素占用空间很大的情况下,顺序表增删元素的时间开销很大(因为主要的时间开销不在查找元素而是在移动元素,并且移动的元素很大),而链表的时间开销仍能保持在一个较小的数值(因为链表主要的时间开销在于移动指针寻找节点,所以才节点大小很大的时候仍能保证一定的速度)。
此时时间开销他们二者虽然都是O(n)但是在面对较多的增删操作的情况下一般会选择链表实现。
2.4.9.6 基本操作-查
-
顺序表
按位查找:O(1)
按值查找:O(n),若表内元素有序,可在O(log2n)时间内找到 -
链表
按位查找:O(n)
按值查找:O(n)
2.4.9.7 顺序、链式、静态、动态四种存储方式的比较
- 顺序存储的固有特点:
逻辑顺序与物理顺序一直,本质上是用数组存储线性表的各个元素(即随机存取);存储密度大,存储空间利用率高。 - 链式存储的固有特点:
元素之间的关系采用这些元素所在的节点的“指针”信息表示(插、删不需要移动节点)。 - 静态存储的固有特点:
在程序运行的过程中不要考虑追加内存的分配问题。 - 动态存储的固有特点:
可动态分配内存;有效的利用内存资源,使程序具有可扩展性。
2.4.9.8 存储密度的问题
-
存储密度:
在数据结构中,结点数据本身所占的存储量和整个结点结构所占的存储量之比。
存储密度 = 结点数据本身所占存储量 / 整个结点结构所占的存储量 -
顺序表的存储密度等于1
-
单链表的存储密度小于1
-
假设单链表的结点的数据占的存储量为N,结点的指针域所占的存储量为M,则存储密度 = N / (N+M),所以单链表的密度是小于1的。
2.4.9.9 存储方式的选择以及二者优劣的答题思路(综述优劣,细谈情况)


相关文章:

24考研数据结构-第二章:线性表
目录 第二章:线性表2.1线性表的定义(逻辑结构)2.2 线性表的基本操作(运算)2.3 线性表的物理/存储结构(确定了才确定数据结构)2.3.1 顺序表的定义2.3.1.1 静态分配2.3.1.2 动态分配2.3.1.3 mallo…...

Mybatis 动态 sql 是做什么的?都有哪些动态 sql?能简述动态 sql 的执行原理不?
OGNL表达式 OGNL,全称为Object-Graph Navigation Language,它是一个功能强大的表达式语言,用来获取和设置Java对象的属性,它旨在提供一个更高的更抽象的层次来对Java对象图进行导航。 OGNL表达式的基本单位是"导航链"&a…...
> fnChkSstStt)
250_C++_typedef std::function<int(std::vector<int> vtBits)> fnChkSstStt
假设我们需要定义一个函数类型来表示一个能够计算整数向量中所有元素之和的函数。 首先,我们定义一个函数,它的参数是一个 std::vector 类型的整数向量,返回值是 int 类型,表示所有元素之和: int sumVectorElements(std::vector<int> vt) {int sum = 0;for (int n…...

无涯教程-jQuery - Transfer方法函数
Transfer 效果可以与effect()方法一起使用。这会将元素的轮廓转移到另一个元素。尝试可视化两个元素之间的交互时非常有用。 Transfer - 语法 selector.effect( "transfer", {arguments}, speed ); 这是所有参数的描述- className - 传输元素将收到的可选类名。…...

openGauss学习笔记-24 openGauss 简单数据管理-模式匹配操作符
文章目录 openGauss学习笔记-24 openGauss 简单数据管理-模式匹配操作符24.1 LIKE24.2 SIMILAR TO24.3 POSIX正则表达式 openGauss学习笔记-24 openGauss 简单数据管理-模式匹配操作符 数据库提供了三种独立的实现模式匹配的方法:SQL LIKE操作符、SIMILAR TO操作符…...
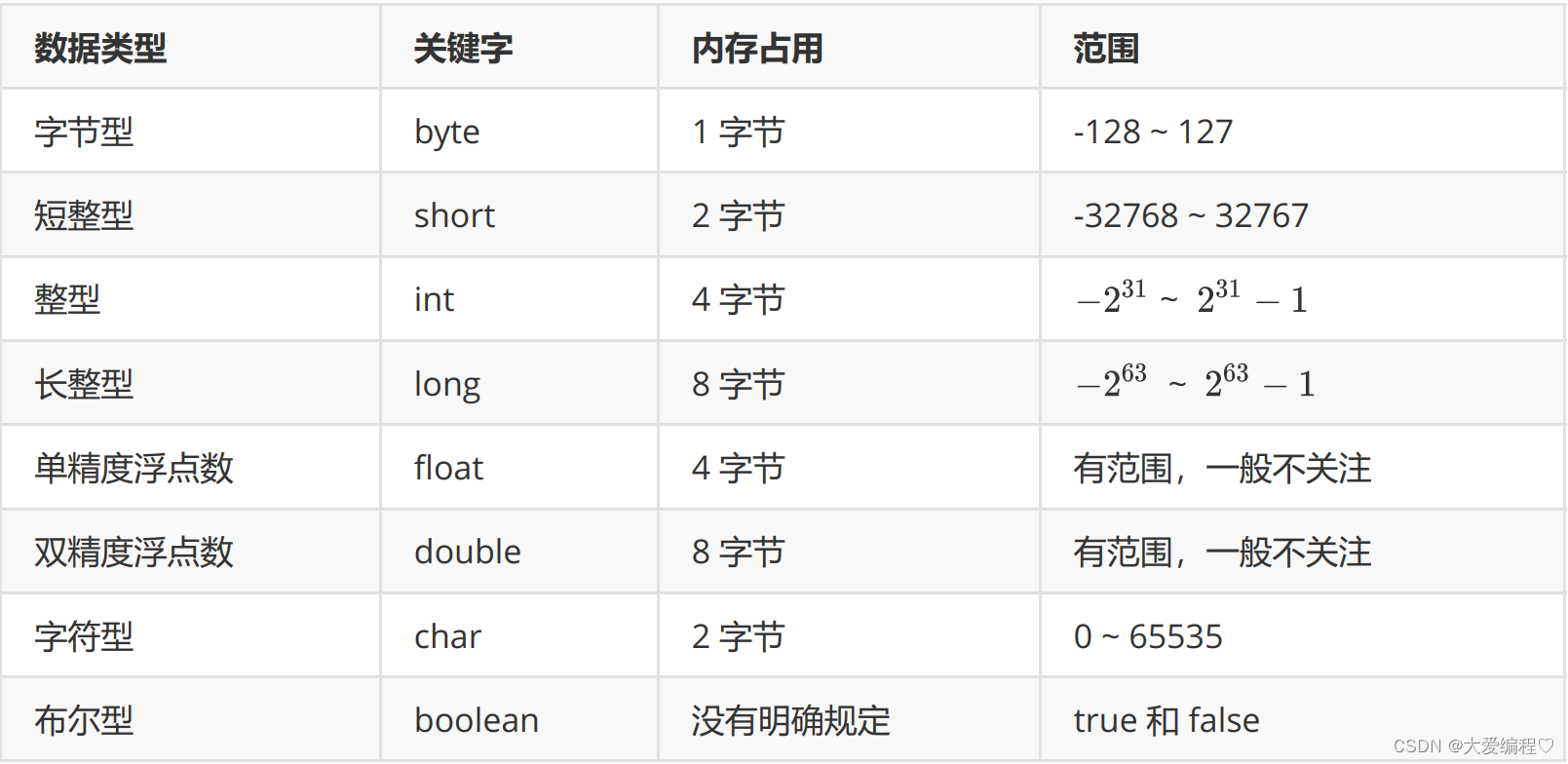
JAVASE---数据类型与变量
1. 字面常量 常量即程序运行期间,固定不变的量称为常量,比如:一个礼拜七天,一年12个月等。 public class Demo{ public static void main(String[] args){ System.Out.println("hello world!"); System.Out.println(…...
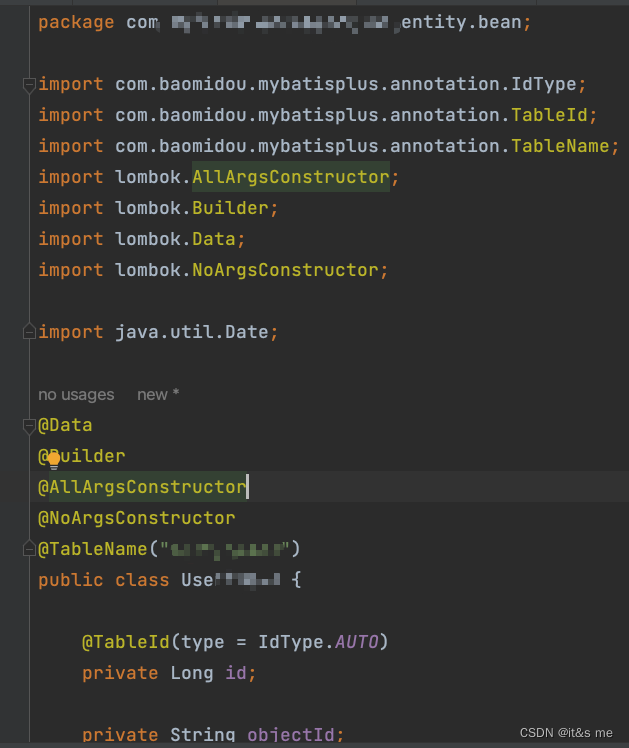
IDEA Groovy 脚本一键生成实体类<mybatisplus>
配置数据库(mysql) 一键生成(右键点击table) 配置自己的groovy脚本 import com.intellij.database.model.DasTable import com.intellij.database.util.Case import com.intellij.database.util.DasUtil import com.intellij.data…...

无涯教程-jQuery - Puff方法函数
吹气效果可以与show/hide/toggle一起使用。通过按比例放大元素并同时隐藏它,可以形成粉扑效果。 Puff - 语法 selector.hide|show|toggle( "puff", {arguments}, speed ); 这是所有参数的描述- model - 效果的模式。可以是"显…...

什么叫前后端分离?为什么需要前后端问题?解决了什么问题?
单体架构出现的问题 引出:来看一个单体项目架构的结构 通过上述可以看到单体架构主要存在以下几点问题: 开发人员同时负责前端和后端代码开发,分工不明确开发效率低前后端代码混合在一个工程中,不便于管理对开发人员要求高(既会前…...
(答案))
Vector<T> 动态数组(随机访问迭代器)(答案)
答案如下 //------下面的代码是用来测试你的代码有没有问题的辅助代码,你无需关注------ #include <algorithm> #include <cstdlib> #include <iostream> #include <vector> #include <utility> using namespace std; struct Record { Record…...

Istio 故障注入与重试的实验
故障注入 Istio流量治理有故障注入的功能,在接收到用户请求程序的流量时,注入故障现象,例如注入HTTP请求错误,当有流量进入Sidecar时,直接返回一个500的错误请求代码。 通过故障注入可以用来测试整个应用程序的故障恢…...

Java设计模式-中介者模式
中介者模式 1.中介者模式含义 中介者模式,就是用一个中介对象来封装一系列的对象交互。中介者使各对象不需要显式地互相引用,从而使其耦合松散,而且可以独立的改变它们之间的交互。 其实中介者模式很简单的,就像它的名字一样&a…...

OpenCV实现高斯模糊加水印
# coding:utf-8 # Email: wangguisendonews.com # Time: 2023/4/21 10:07 # File: utils.pyimport cv2 import PIL from PIL import Image import numpy as np from watermarker.marker import add_mark, im_add_mark import matplotlib.pyplot as plt# PIL Image转换成OpenCV格…...
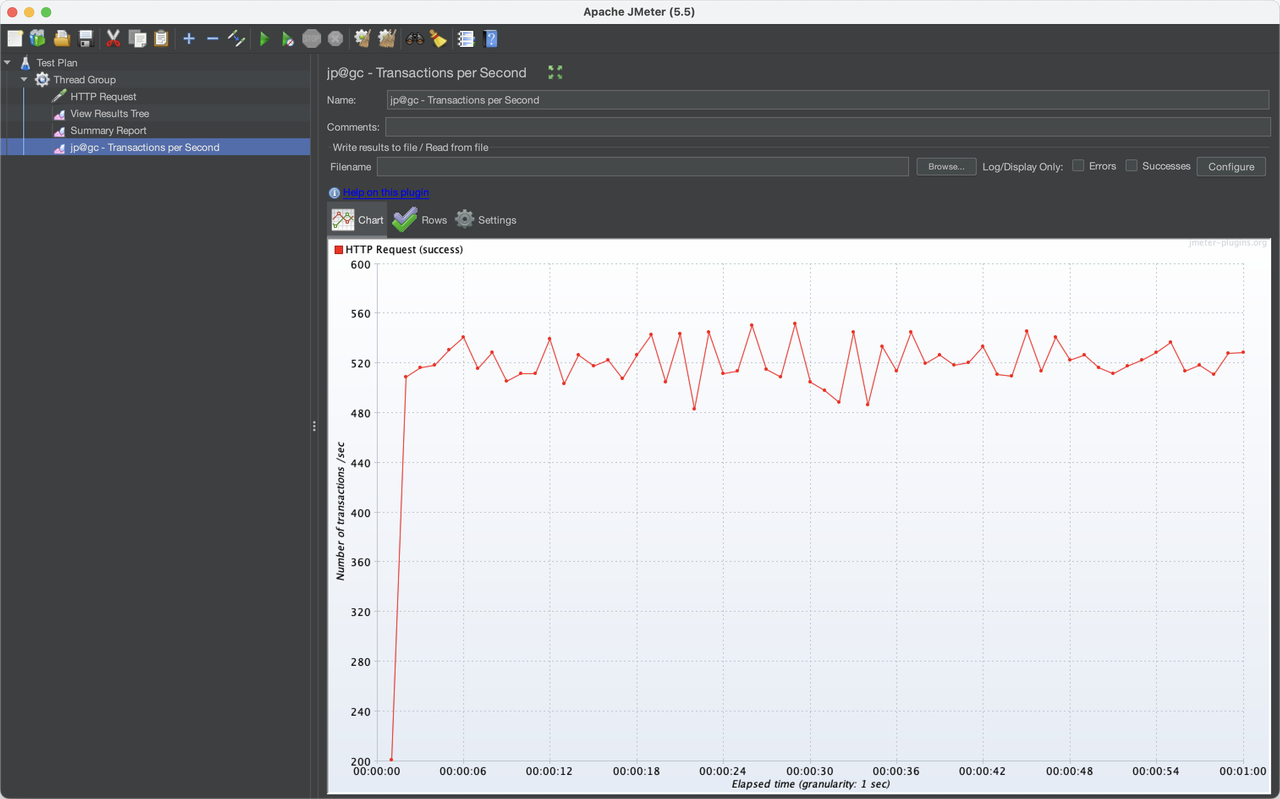
JMeter 怎么查看 TPS 数据教程,简单易懂
TPS 是软件测试结果的测量单位。一个事务是指一个客户机向服务器发送请求然后服务器做出反应的过程。客户机在发送请求时开始计时,收到服务器响应后结束计时,以此来计算使用的时间和完成的事务个数。在 JMeter 中,我们可以使用以下方法查看 T…...

2023年的深度学习入门指南(19) - LLaMA 2源码解析
2023年的深度学习入门指南(19) - LLaMA 2源码解析 上一节我们学习了LLaMA 2的补全和聊天两种API的使用方法。本节我们来看看LLaMA 2的源码。 补全函数text_completion源码解析 上一节我们讲了LLaMA 2的编程方法。我们来复习一下: generator Llama.build(ckpt_di…...

慕课网Go-2.数组、slice、map、list
数组 package mainimport "fmt"func main() {var course1 [3]stringcourse1[0] "go"course1[1] "grpc"course1[2] "gin"for _, value : range course1 {fmt.Println(value)}course2 : [3]string{2: "grpc"}fmt.Println(…...

Django的Rest framework搭建自定义授权登录
系列文章目录 提示:阅读本章之前,请先阅读目录 文章目录 系列文章目录一、前言User模型User的viewsUser的serializersutils的md5加密自定义认证方法配置路由总路由分路由rest的配置 一、前言 之前的文章有写过通过jwt认证的文章,今天这一篇是…...

01 矩阵(力扣)多源广度优先搜索 JAVA
给定一个由 0 和 1 组成的矩阵 mat ,请输出一个大小相同的矩阵,其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。 两个相邻元素间的距离为 1 。 输入:mat [[0,0,0],[0,1,0],[0,0,0]] 输出:[[0,0,0],[0,1,0],[0,0,0]] 输入…...
怎么绘制简爱思维导图?用这个工具绘制很简单
怎么绘制简爱思维导图?绘制思维导图是一项非常有用的技能,有助于梳理思路、整理知识、更好地理解和记忆信息。因此,无论你是学生、教师、工程师、项目经理或者只是想要更好地组织自己的想法,学会绘制思维导图都是非常有益的。下面…...
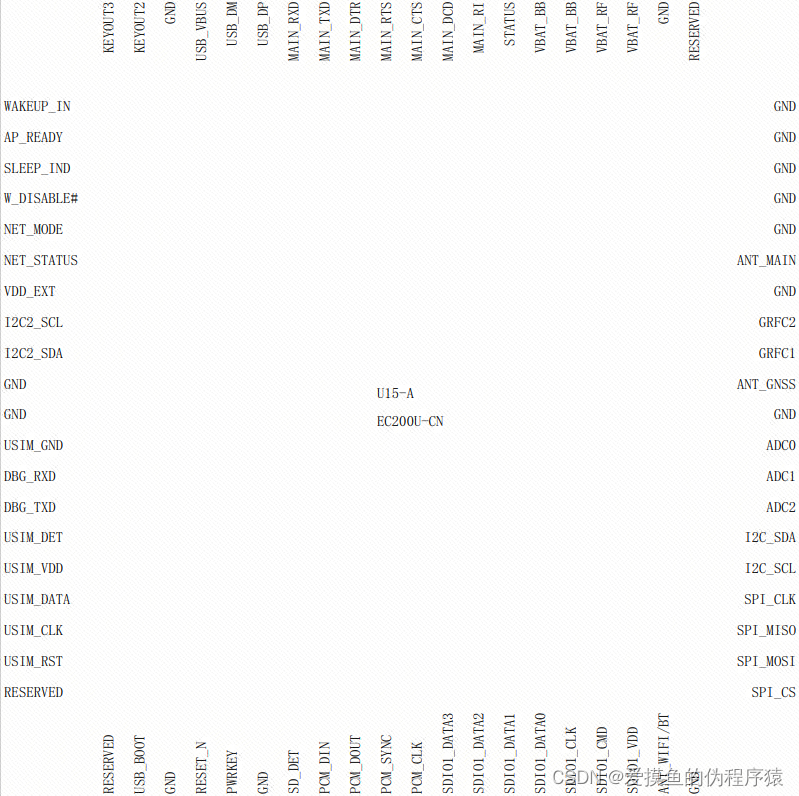
EC200U-CN学习(三)
EC200U系列内置丰富的网络协议,集成多个工业标准接口,并支持多种驱动和软件功能(适用于Windows 7/8/8.1/10、Linux和Android等操作系统下的USB驱动),极大地拓展了其在M2M领域的应用范围,如POS、POC、ETC、共…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
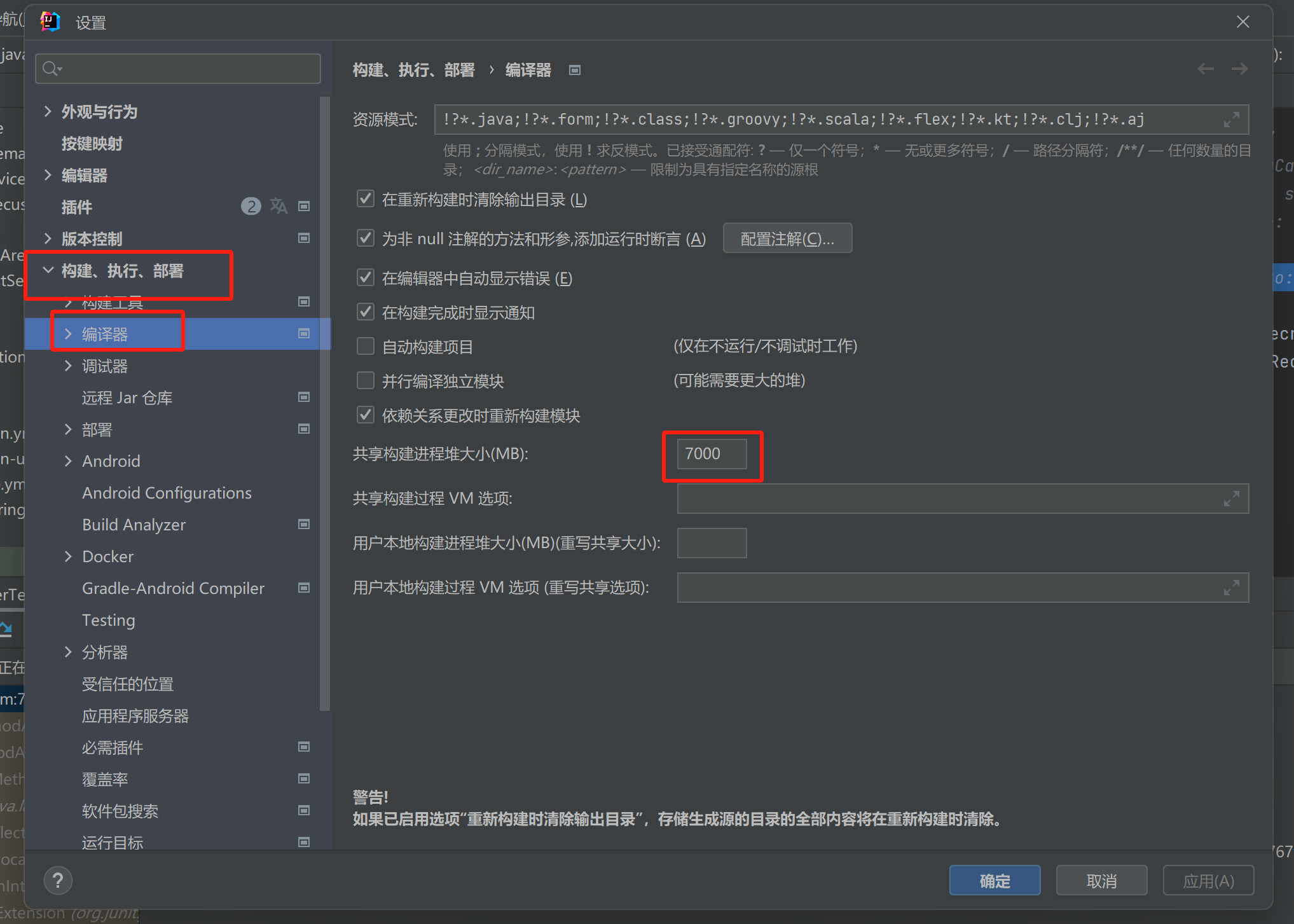
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...
