数据结构:树的存储结构
学习树之前,我们已经了解了二叉树的顺序存储和链式存储,哪么我们如何来存储普通型的树结构的数据?如下图1:

如图1所示,这是一颗普通的树,我们要如何来存储呢?通常,存储这种树结构的数据的方法有3中:
- 双亲表示法。
- 孩子表示法。
- 孩子兄弟表示法。
双亲表示法
双亲表示法采用顺序表(也就是数组)存储普通树,核心思想:顺序存储各个节点的同时,给各个节点附加一个记录其父节点位置的变量。
注意:根结点没有父节点,因此根结点记录父节点位置的变量一般为-1。
例如,采用双亲表示法存储图1中的普通树,其存储状态如图2所示:

图2存储普通树转化为代码为:
#define MAX_SIZE 100//定义树中结点最大数量
typedef struct node{char data;//树中结点的数据int parent;//结点的父节点再数组中的位置下标
};typedef struct {node arr[MAX_SIZE];//存放树中所有结点int n;//节点数
}Tree;
因此,存储图1中普通树的实现代码为:
#include "iostream"using namespace std;
#define MAX_SIZE 100//定义树中结点最大数量
typedef struct node{char data;//树中结点的数据int parent;//结点的父节点再数组中的位置下标
};typedef struct {node arr[MAX_SIZE];//存放树中所有结点int n;//节点数
}Tree;Tree Init(Tree tree){cout << "请输入结点个数:" << endl;cin >> tree.n;cout << "请输入结点的值其双亲位于数组中的位置下标:" << endl;for(int i = 0; i < tree.n; i++){cin >> tree.arr[i].data >> tree.arr[i].parent;}return tree;
}void FindParent(Tree tree){char a;bool IsFind = false;cout << "请输入要查询的节点值:" << endl;cin >> a;for(int i = 0; i < tree.n; i++){if(tree.arr[i].data == a){IsFind = true;cout << a << "的父节点为" << tree.arr[tree.arr[i].parent].data << ",存储位置下标为" << tree.arr[i].parent << endl;break;}}
}
int main(){Tree tree;for(int i = 0; i < MAX_SIZE; i++){tree.arr[i].parent = -1;tree.arr[i].data = ' ';}tree = Init(tree);FindParent(tree);return 0;
}
程序运行实例:
请输入结点个数:
10
请输入结点的值其双亲位于数组中的位置下标:
R -1
A 0
B 0
C 0
D 1
E 1
F 3
G 6
H 6
K 6
请输入要查询的节点值:
C
C的父节点为R,存储位置下标为0
孩子表示法
孩子表示法是采用“顺序表+链表”的组合结构,其存储过程是:从树的根结点开始,使用顺序表依次存储树中各个节点,需要注意的是,与双亲表示法不同,孩子表示法会给各个节点配备一个链表,用于存储各个节点的孩子节点位于顺序表中的位置。
如果孩子没有叶子节点,则该节点的链表为空链表。
例如,使用孩子表示法存储图3a中的树,则最终存储状况如图3b所示:

代码实现如下:
#include "iostream"using namespace std;
#define MAX_SIZE 100//定义树中结点最大数量
typedef struct node{int child;//链表中每个结点存储的是数据再数组中存储的位置下标struct node *next;
};
typedef struct {char data;//结点的数据node * FirstChild;//孩子链表的头节点
}box;
typedef struct {box arr[MAX_SIZE];//存放树中所有结点int n, r;//节点数和树根的位置
}Tree;Tree Init(Tree tree){cout << "请输入结点个数:";cin >> tree.n;for(int i = 0; i < tree.n; i++){cout << "输入第" << i + 1 << "个节点的值:" ;cin >> tree.arr[i].data;tree.arr[i].FirstChild = new node;tree.arr[i].FirstChild->next = NULL;cout << "输入结点" << tree.arr[i].data << "的孩子结点的数量:";int num = 0;cin >> num;if(num != 0){node *p = tree.arr[i].FirstChild;for(int j = 0; j < num; j++){node *ptr = new node;ptr->next = NULL;cout << "输入第" << j + 1 << "个孩子节点在顺序表中的位置: ";cin >> ptr->child;p->next = ptr;p = p->next;}}}return tree;
}void FindKids(Tree tree, char ch){bool IsFind = false;for(int i = 0; i < tree.n; i++){if(tree.arr[i].data == ch){node *p = tree.arr[i].FirstChild->next;while(p){IsFind = true;cout << tree.arr[p->child].data;p = p->next;}break;}}
}
int main(){Tree tree;tree.r = 0;//默认根结点的下标为0for(int i = 0; i < MAX_SIZE; i++){tree.arr[i].FirstChild = NULL;}tree = Init(tree);FindKids(tree, 'F');//找出结点F的所有孩子结点return 0;
}
程序运行结果如下:
请输入结点个数:10
输入第1个节点的值:R
输入结点R的孩子结点的数量:3
输入第1个孩子节点在顺序表中的位置: 1
输入第2个孩子节点在顺序表中的位置: 2
输入第3个孩子节点在顺序表中的位置: 3
输入第2个节点的值:A
输入结点A的孩子结点的数量:2
输入第1个孩子节点在顺序表中的位置: 4
输入第2个孩子节点在顺序表中的位置: 5
输入第3个节点的值:B
输入结点B的孩子结点的数量:0
输入第4个节点的值:C
输入结点C的孩子结点的数量:1
输入第1个孩子节点在顺序表中的位置: 6
输入第5个节点的值:D
输入结点D的孩子结点的数量:0
输入第6个节点的值:E
输入结点E的孩子结点的数量:0
输入第7个节点的值:F
输入结点F的孩子结点的数量:3
输入第1个孩子节点在顺序表中的位置: 7
输入第2个孩子节点在顺序表中的位置: 8
输入第3个孩子节点在顺序表中的位置: 9
输入第8个节点的值:G
输入结点G的孩子结点的数量:0
输入第9个节点的值:H
输入结点H的孩子结点的数量:0
输入第10个节点的值:K
输入结点K的孩子结点的数量:0
找出节点 F 的所有孩子节点:GHK
使用孩子表示法存储的树结构,正好和双亲表示法相反,适用于 查找某个节点的孩子结点,不适用于查找父节点。
其实,我们也可以将双亲表示法和孩子表示法相互结合,就可以得到如图4所示:

使用图4结果存储普通树,技能快速找到指定节点的父节点,也能快速找到指定结点的孩子结点。
孩子兄弟表示法
孩子兄弟表示法:采用的是链式存储结构,其思想是,从树的根结点开始,依次用链表存储各个节点的孩子结点和兄弟节点。
所以,该链表中的结点包括3个部分,如图5所示:
- 结点的值。
- 指向孩子结点的指针。
- 指向兄弟结点的指针。

代码表示如下:
typedef struct node{char data;struct node *ForstChild, *NextSibling;
};
还是以图1为例,使用孩子兄弟表示法进行存储的结果如图所示:

由图我们可以发现,孩子兄弟表示法是用二叉树的左子树存储树的孩子结点,用右子树来存储兄弟结点。
孩子兄弟表示法可以作为将普通树转化为二叉树的最有效的方法,同时这个方法也被称之为“二叉树表示法”或者”二叉链表表示法“
相关文章:

数据结构:树的存储结构
学习树之前,我们已经了解了二叉树的顺序存储和链式存储,哪么我们如何来存储普通型的树结构的数据?如下图1: 如图1所示,这是一颗普通的树,我们要如何来存储呢?通常,存储这种树结构的数…...
Vue前端渲染blob二进制对象图片的方法
近期做开发,联调接口。接口返回的是一张图片,是对二进制图片处理并渲染,特此记录一下。 本文章是转载文章,原文章:Vue前端处理blob二进制对象图片的方法 接口response是下图 显然,获取到的是一堆乱码&…...
Java的标记接口(Marker Interface)
Java中的标记接口(Marker Interface)是一个空接口,接口内什么也没有定义。它标识了一种能力,标识继承自该接口的接口、实现了此接口的类具有某种能力。 例如,jdk的com.sun.org.apache.xalan.internal.xsltc.trax.Temp…...
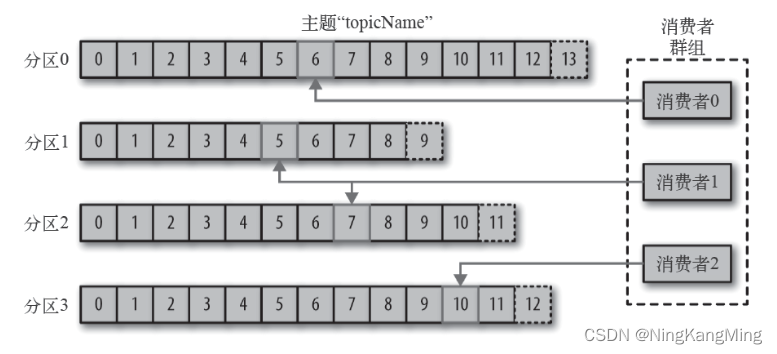
Kafka基础架构与核心概念
Kafka简介 Kafka是由Apache软件基金会开发的一个开源流处理平台,由Scala和Java编写。Kafka是一种高吞吐量的分布式发布订阅消息系统,它可以处理消费者在网站中的所有动作流数据。架构特点是分区、多副本、多生产者、多订阅者,性能特点主要是…...
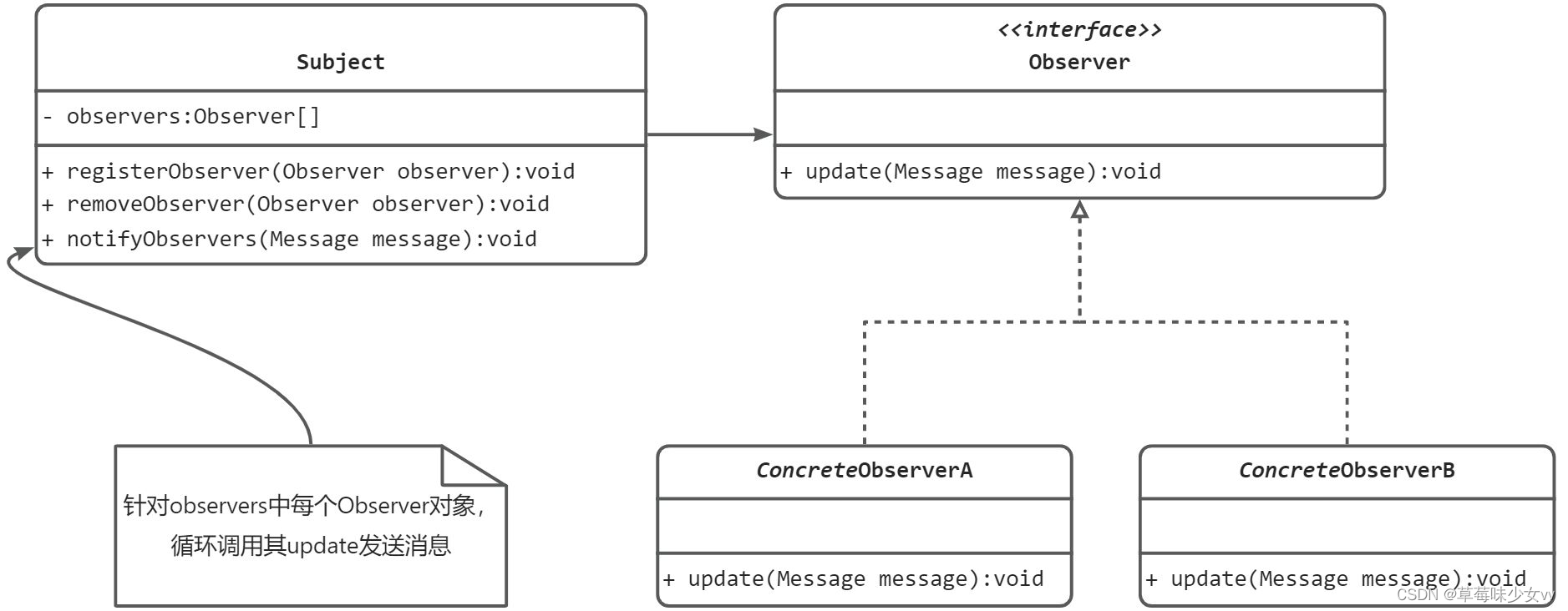
观察者模式与观察者模式实例EventBus
什么是观察者模式 顾名思义,观察者模式就是在多个对象之间,定义一个一对多的依赖,当一个对象状态改变时,所有依赖这个对象的对象都会自动收到通知。 观察者模式也称为发布订阅模式(Publish-Subscribe Design Pattern)࿰…...

科普 | OSI模型
本文简要地介绍 OSI 模型 1’ 2’ 3。 更新:2023 / 7 / 23 科普 | OSI模型 术语节点链路协议网络拓扑 概念作用结构应用层表示层会话层传输层网络层数据链路层物理层 数据如何流动OSI 和TCP/IP 的对应关系和协议参考链接 术语 节点 节点( Node &#…...

redis相关异常之RedisConnectionExceptionRedisCommandTimeoutException
本文只是分析Letture类型的Redis 池化连接出现的连接超时异常、读超时异常问题。 1.RedisConnectionException 默认是10秒。 通过如下可以配置: public class MyLettuceClientConfigurationBuilderCustomizer implements LettuceClientConfigurationBuilderCusto…...

Merge the squares! 2023牛客暑期多校训练营4-H
登录—专业IT笔试面试备考平台_牛客网 题目大意:有n*n个边长为1的小正方形摆放在边长为n的大正方形中,每次可以选择不超过50个正方形,将其合并为一个更大的正方形,求一种可行的操作使所有小正方形都被合并成一个n*n的大正方形 1…...
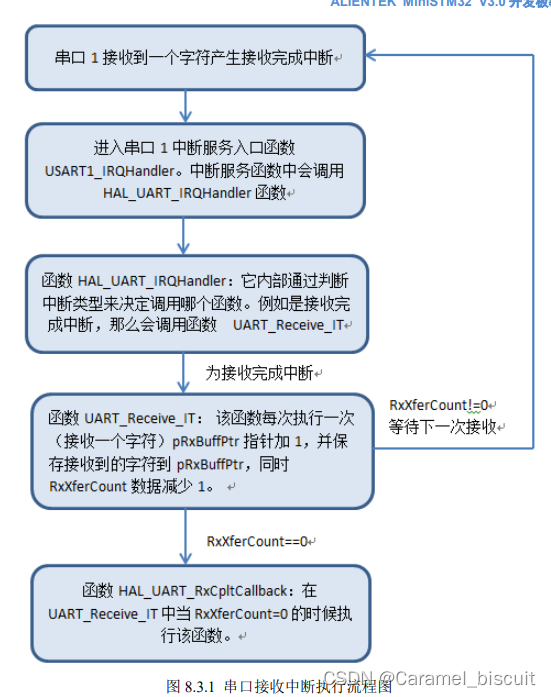
STM32 串口学习(二)
要用跳线帽将PA9与RXD相连,PA10与TXD相连。 软件设计 void uart_init(u32 baud) {//UART 初始化设置UART1_Handler.InstanceUSART1; //USART1UART1_Handler.Init.BaudRatebound; //波特率UART1_Handler.Init.WordLengthUART_WORDLENGTH_8B; //字长为 8 位数据格式U…...
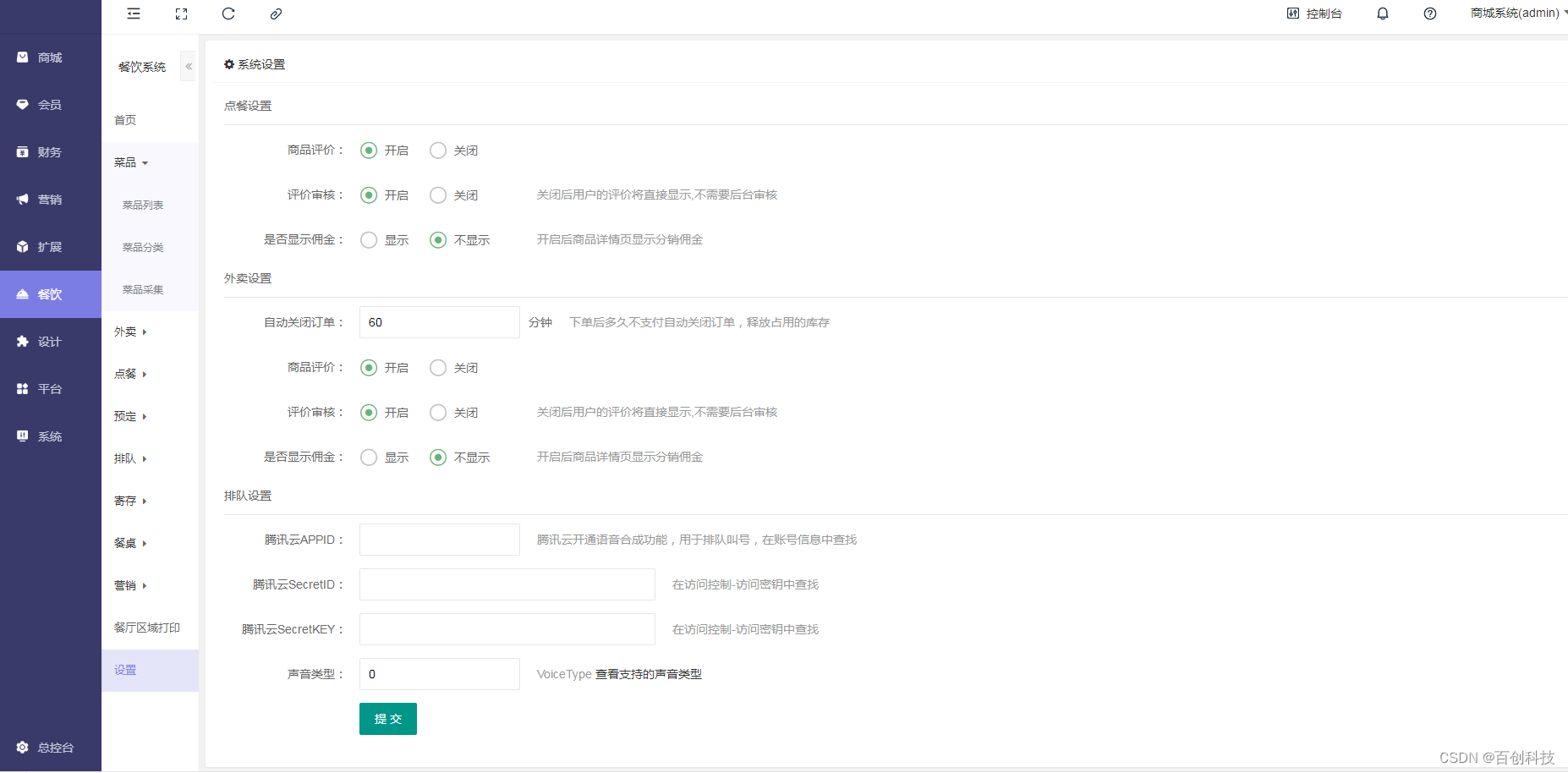
点大商城V2_2.5.0 全开源版 商家自营+多商户入驻 百度+支付宝+QQ+头条+小程序端+unipp开源前端安装测试教程
安装测试环境:Nginx 1.20PHP7.2MySQL 5.6 修复了无法上传开放平台问题 安装说明: 1、上传后端目录至网站 2、导入提供的数据库文件 3、修改数据库配置文件根目录下config.php,增加数据库用户名和密码 4、网站后台直接访问网址ÿ…...

“深入理解SpringBoot:从入门到精通“
标题:深入理解Spring Boot:从入门到精通 摘要:本文将介绍Spring Boot的基本概念和核心特性,并通过示例代码演示如何使用Spring Boot构建一个简单的Web应用程序。 1. 简介 Spring Boot是一个开源的Java框架,旨在简化基…...

PCB绘制时踩的坑 - SOT-223封装
SOT-223封装并不是同一的,细分的话可以分为两种常用的封装。尤其是tab脚的属性很容易搞错。如果你想着用tab脚连接有属性的铺铜,来提高散热效率,那么你一定要注意你购买的器件tab脚的属性。 第一种如下图,第1脚为GND,第…...
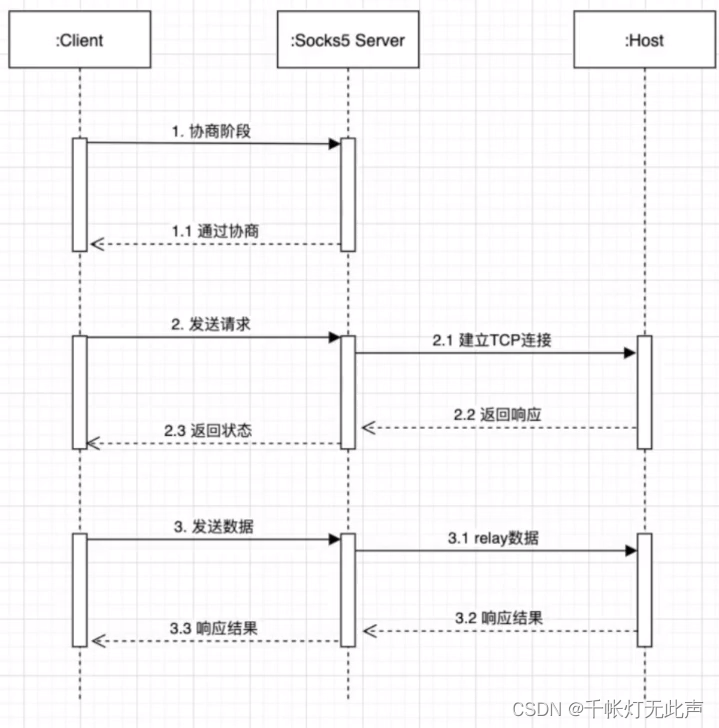
Go语法入门 + 项目实战
👂 Take me Hand Acoustic - Ccile Corbel - 单曲 - 网易云音乐 第3个小项目有问题,不能在Windows下跑,懒得去搜Linux上怎么跑了,已经落下进度了.... 目录 😳前言 🍉Go两小时 🔑小项目实战 …...
QT控件通过qss设置子控件的对齐方式、大小自适应等
一些复杂控件,是有子控件的,每个子控件,都可以通过qss的双冒号选择器来选中,进行独特的样式定义。很多控件都有子控件,太多了,后面单独写一篇文章来介绍各个控件的子控件。这里就随便来几个例子 例如下拉列…...

基于java在线收银系统设计与实现
摘要 科技的力量总是在关键的地方改变着人们的生活,不仅如此,我们的生活也是离不开这样或者那样的科技改变,有的消费者没有时间去商场购物,那么电商和快递的结合让端口到消费者的距离不再遥远;有的房客因地域或者工作的…...
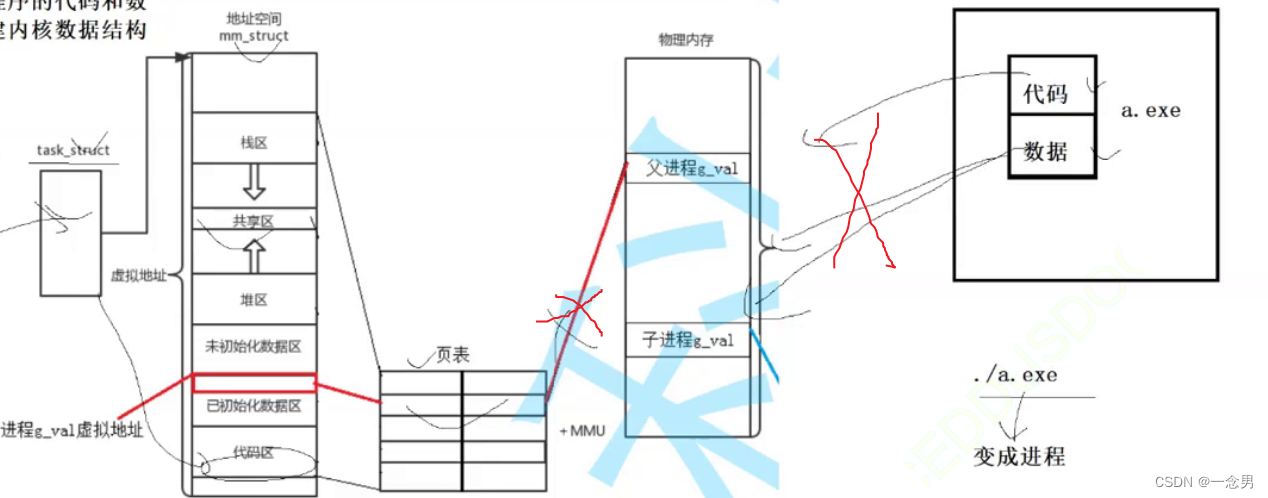
Linux--进程的新建状态
新建状态: 操作系统创建了进程的内核数据结构(task_struct、mm_struct、页表),但是页表没有创建映射关系,而且磁盘里的程序的代码和数据未加载到物理内存...

区间dp,合并石子模板题
设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的…...

C++代码格式化工具clang-format详细介绍
文章目录 clang-format思考代码风格指南生成您的配置运行 clang-format禁用一段代码的格式设置clang-format的设置预览 clang-format 我曾在许多编程团队工作过,这些团队名义上都有“编程风格指南”。该指南经常被写下来并放置在开发人员很少查看的地方。几乎在每种…...
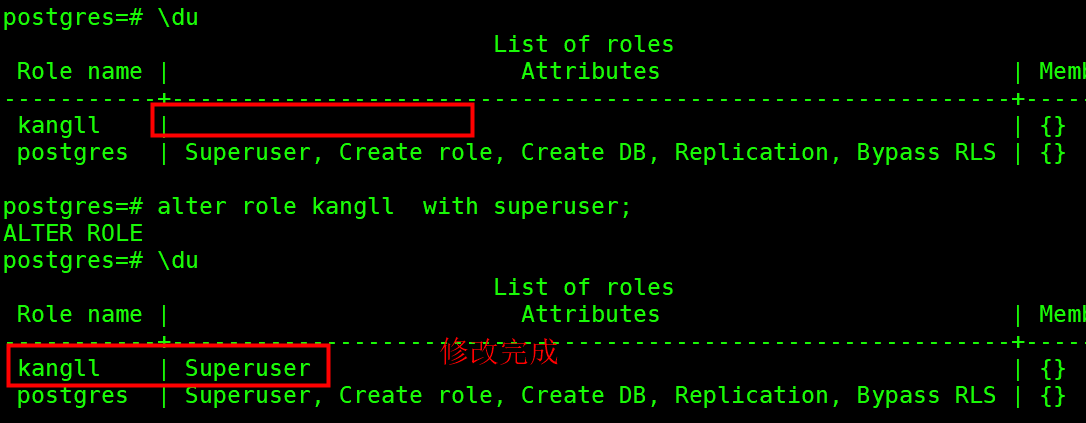
CentOS 7安装PostgreSQL 15版本数据库
目录 一、何为PostgreSQL? 二、PostgreSQL安装 2.1安装依赖 2.2 执行安装 2.3 数据库初始化 2.4 配置环境变量 2.5 创建数据库 2.6 配置远程 2.7 测试远程 三、常用命令 四、用户创建和数据库权限 一、何为PostgreSQL? PostgreSQL是以加州大学…...

QGraphicsView实现简易地图2『瓦片经纬度』
前文链接:QGraphicsView实现简易地图1『加载离线瓦片地图』 地图采用GCJ02 Web 墨卡托投影,最小坐标:(-180.00000000000000,-85.05112877980655),最大坐标:(180.00000000000000,85.05112877980655)。瓦片地图单张图片像…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
