AtCoder Beginner Contest 312(A~D)
A
//语法题也要更仔细嘞,要不然也会wa
#include <bits/stdc++.h>
// #pragma GCC optimize(3,"Ofast","inline")
// #pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
typedef pair<int, int> PII;
const int N = 1e6 + 10;void solve()
{string s;cin >> s;if(s=="ACE"||s=="BDF"||s=="CEG"||s=="DFA"||s=="EGB"||s=="FAC"||s=="GBD") cout << "Yes" << endl;else cout << "No" << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t -- ) solve(); system("pause"); return 0;
}
B
题意就是从一块大棋盘中抠出一块9*9指定的图案。数据范围不大,没有什么新奇的想法,直接遍历判断的。坐标的转换比较绕人//下次还是从1开始存吧
#include <bits/stdc++.h>
// #pragma GCC optimize(3,"Ofast","inline")
// #pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
typedef pair<int, int> PII;
const int N = 1e6 + 10;
int n, m;
char g[110][110];bool check(int x, int y)
{//左上角3*3的黑色for(int i = 0; i < 3; i ++ )for(int j = 0; j < 3; j ++ ){if(g[x+i][y+j] != '#') return false;}//右下角3*3的黑色for(int i = x + 8; i >= x + 6; i --)for(int j = y + 8; j >= y + 6; j -- )if(g[i][j] != '#') return false;//黑色周围的白色for(int i = 0; i < 4; i ++ ){if(g[x+3][y+i] != '.') return false;if(g[x+i][y + 3] !='.') return false; if(g[x+5][y+8-i] != '.') return false;if(g[x+8-i][y + 5] !='.') return false;}return true;
}void solve()
{ cin >> n >> m;for(int i = 0; i < n; i ++ ){for(int j = 0; j < m; j ++ ) cin >> g[i][j];}for(int i = 0; i < n - 8; i ++ )for(int j = 0; j < m - 8; j ++ ){if(check(i, j)){cout << i + 1<< ' ' << j + 1<< endl;} }}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t -- ) solve(); system("pause"); return 0;
}
C
思路:裸二分题,直接二分答案即可。
二分的时间复杂度是logn,check是n,nlogn能过。也可以给两个数组排序,对于每个mid在数组里二分查找坐标,但是排序的时间复杂度是nlogn,其实是一样的。
#include <bits/stdc++.h>
// #pragma GCC optimize(3,"Ofast","inline")
// #pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
typedef pair<int, int> PII;
const int N = 2e6 + 10;
int a[N], b[N];
int n, m;bool check(int mid)
{int cnt1 = 0, cnt2 = 0;for(int i = 1; i <= n; i ++ )if(a[i] <= mid) cnt1 ++;for(int i = 1; i <= m; i ++ )if(b[i] >= mid) cnt2 ++;return cnt2 <= cnt1;
}void solve()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> a[i];for (int j = 1; j <= m; j ++ ) cin >> b[j];int l = 0, r = 1e9 + 1, mid;//注意右边界不能是1e9,a和b的范围是1e9,但是实际出价的范围可以比1e9多while(l < r){mid = l + r >> 1;if(check(mid)) r = mid;else l = mid + 1;}cout << l << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t -- ) solve(); system("pause"); return 0;
}
D
dp题,f[i,j]表示前 i 个字符,剩余左括号数为 j 的方案数
#include <bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
#pragma GCC optimize(2)
using namespace std;
typedef long long LL;
#define int LL
const int N = 3010, mod = 998244353;
int f[N][N];void solve()
{ string s;cin >> s;s = '0' + s;f[0][0] = 1;for(int i = 1; i < s.size(); i ++ )for(int j = 0; j <= i; j ++ ){if(s[i] == '(') //如果第i位是左括号,那么情况与上一位 左括号数-1的情况相同f[i][j] = f[i - 1][j - 1];else if(s[i] == ')') //如果这位是右括号,情况与上一位 剩余左括号数+1情况相同f[i][j] = f[i - 1][j + 1];else //如果这一位是?,那么相当于可以是左括号也可以是右括号,情况为上面两种的和f[i][j] = (f[i - 1][j + 1] + f[i - 1][j - 1])%mod;}//遍历到最后一个字符串,并且左右括号恰好匹配(无剩余左括号)cout << f[s.size() - 1][0] << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t -- ) solve(); system("pause"); return 0;
}
相关文章:
)
AtCoder Beginner Contest 312(A~D)
A //语法题也要更仔细嘞,要不然也会wa #include <bits/stdc.h> // #pragma GCC optimize(3,"Ofast","inline") // #pragma GCC optimize(2) using namespace std; typedef long long LL; #define int LL typedef pair<int, int> …...

SQL中Partition的相关用法
使用Partition可以根据指定的列或表达式将数据分成多个分区。每个分区都是逻辑上独立的,可以单独进行查询、插入、更新和删除操作。Partition可以提高查询性能,因为它可以限制在特定分区上执行查询,而不是在整个表上执行。 在SQL中ÿ…...
微服务——Docker
docker与虚拟机的区别 首先要知道三个层次 硬件层:计算机硬件 内核层:与硬件交互,提供操作硬件的指令 应用层: 系统应用封装内核指令为函数,便于程序员调用。用户程序基于系统函数库实现功能。 docker在打包的时候直接把应用层的函数库也进行打包&a…...

测试|测试用例方法篇
测试|测试用例方法篇 文章目录 测试|测试用例方法篇1.测试用例的基本要素:测试环境,操作步骤,测试数据,预期结果…2.测试用例带来的好处3.测试用例的设计思路,设计方法,具体设计方法之间的关系**设计测试用…...

负载均衡的策略有哪些? 负载均衡的三种方式?
负载均衡的策略有哪些? 负载均衡的策略有如下: 1. 轮询(Round Robin):按照请求的顺序轮流分配到不同的服务器。 2. 权重(Weighted):给不同的服务器分配不同的权重,根据权重比例来…...
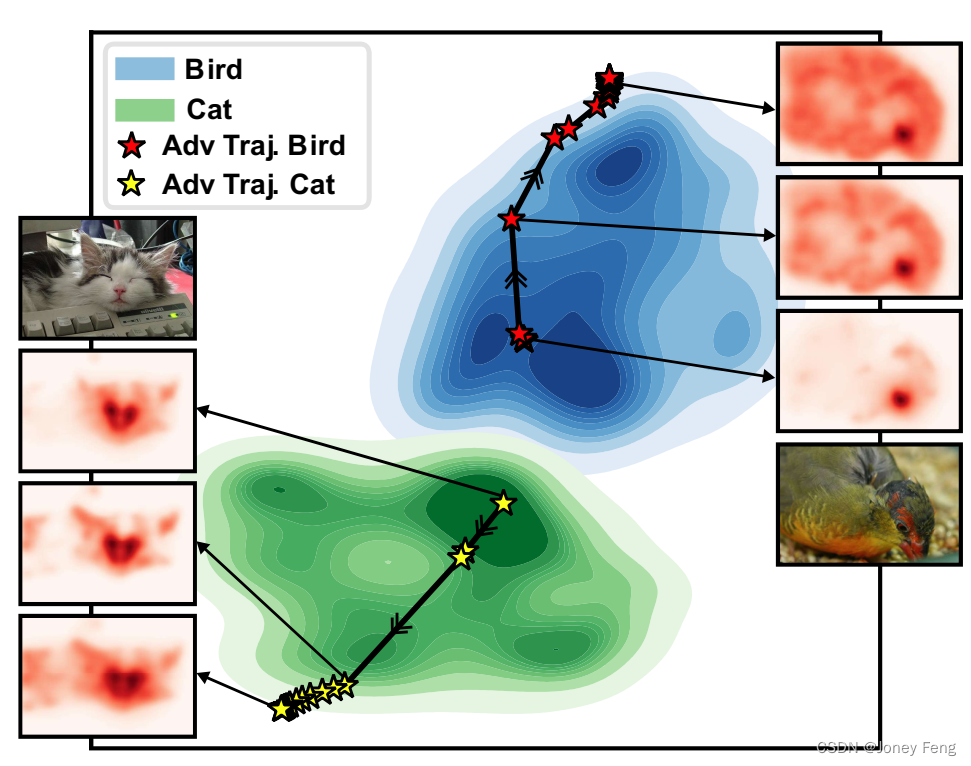
二十三章:抗对抗性操纵的弱监督和半监督语义分割的属性解释
0.摘要 弱监督语义分割从分类器中生成像素级定位,但往往会限制其关注目标对象的一个小的区域。AdvCAM是一种图像的属性图,通过增加分类分数来进行操作。这种操作以反对抗的方式实现,沿着像素梯度的相反方向扰动图像。它迫使最初被认为不具有区…...

curator实现的zookeeper可重入锁
Curator是一个Apache开源的ZooKeeper客户端库,它提供了许多高级特性和工具类,用于简化在分布式环境中使用ZooKeeper的开发。其中之一就是可重入锁。 Curator提供了InterProcessMutex类来实现可重入锁。以下是使用Curator实现ZooKeeper可重入锁的示例&am…...
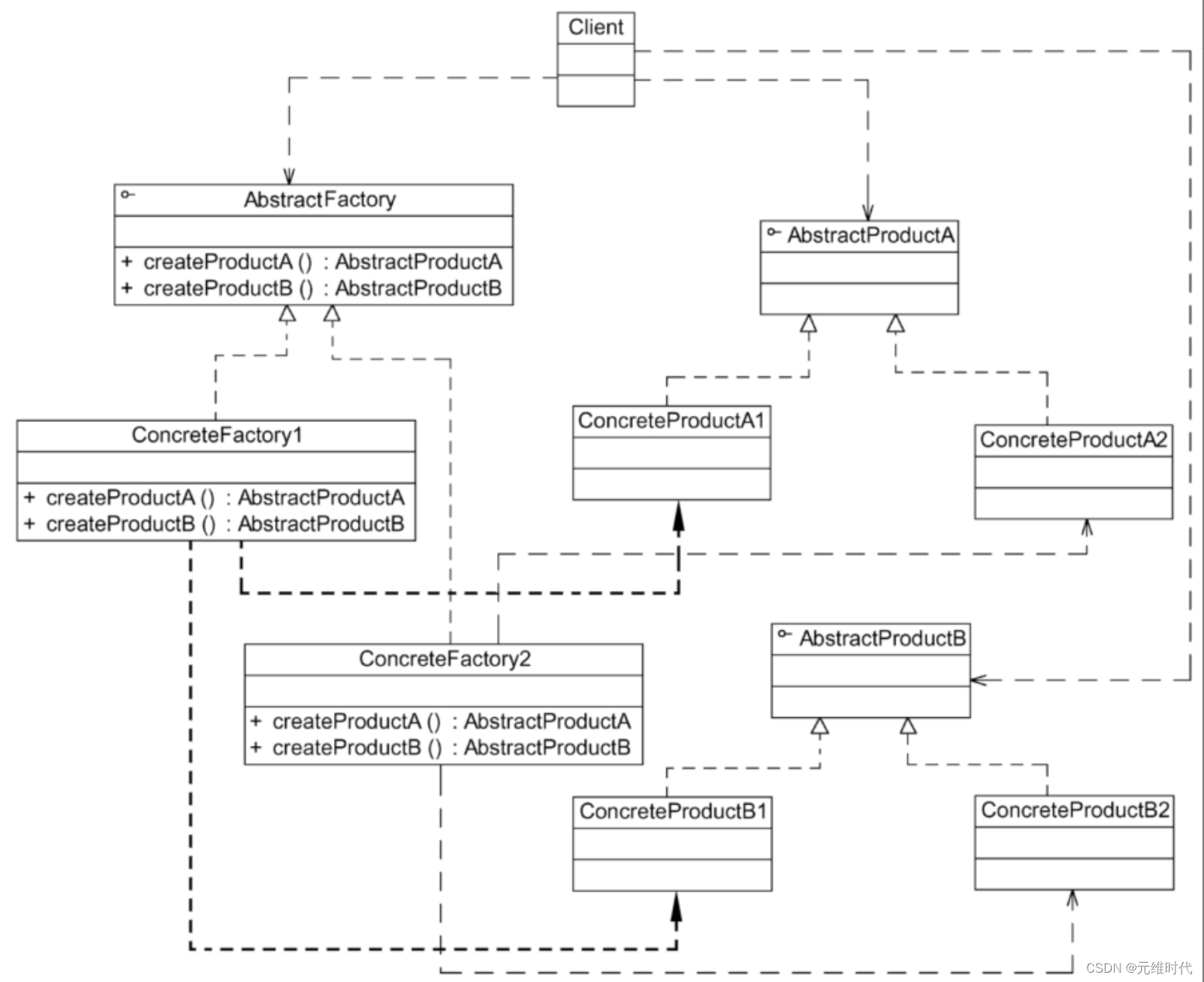
抽象工厂模式——产品族的创建
1、简介 1.1、简介 抽象工厂模式为创建一组对象提供了一种解决方案。与工厂方法模式相比,抽象工厂模式中的具体工厂不只是创建一种产品,它负责创建一族产品 1.2、定义 抽象工厂模式(Abstract Factory Pattern):提供…...

【C语言初阶篇】自定义类型结构体我不允许还有人不会!
🎬 鸽芷咕:个人主页 🔥 个人专栏:《C语言初阶篇》 《C语言进阶篇》 ⛺️生活的理想,就是为了理想的生活! 文章目录 📋 前言1 . 什么是结构体1.1 结构的定义1.2 结构的声明 2.结构体初始化2.1 用标签名定义和初始化2.2…...

重大更新|Sui主网即将上线流动性质押,助力资产再流通
Sui社区一直提议官方上线流动质押功能,现在通过SIP过程,已经升级该协议以实现这一功能。 Sui使用委托权益证明机制(DPoS)来选择和奖励负责运营网络的验证节点。为了保障网络安全,验证节点通过质押SUI token获得质押奖…...

day3 驱动开发 c语言编程
通过ioctl(内核应用层) 控制led灯三盏,风扇,蜂鸣器,小马达 头文件head.h #ifndef __LED_H__ #define __LED_H__typedef struct {volatile unsigned int TZCR; // 0x000volatile unsigned int res1[2]; // 0x…...
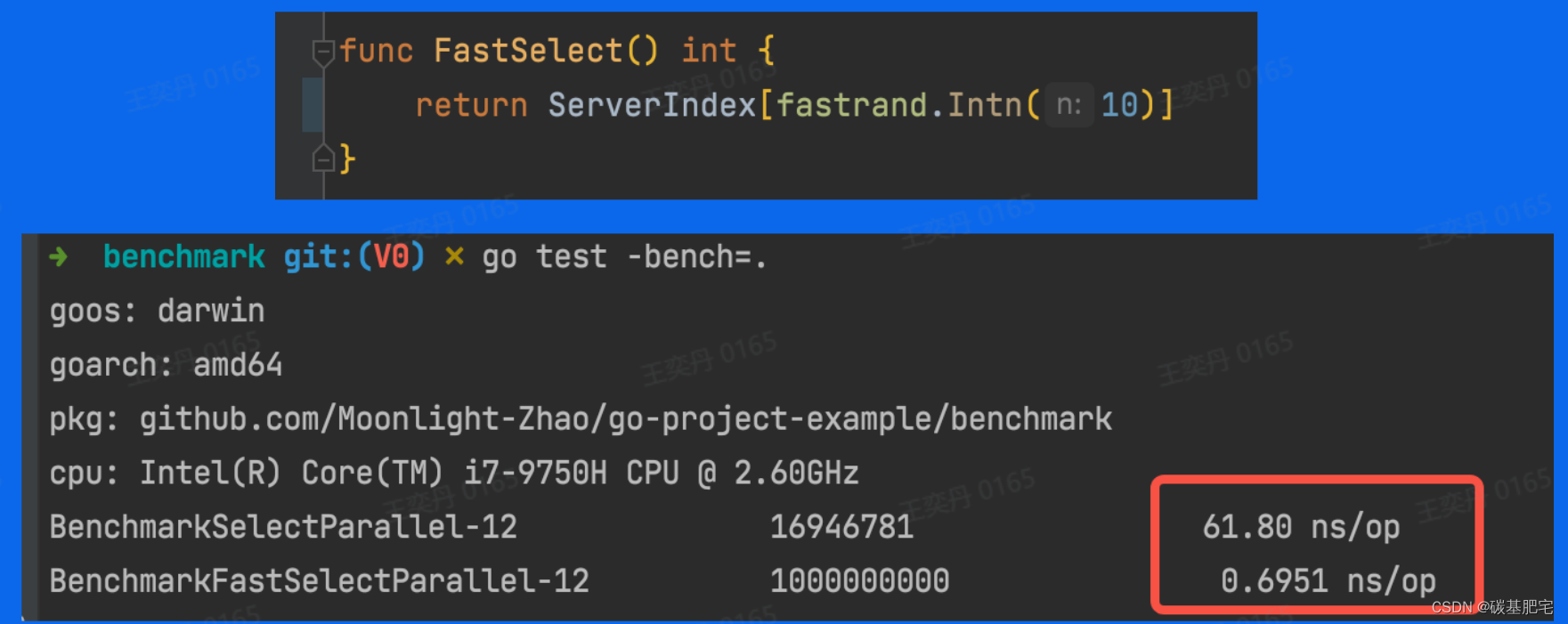
【字节跳动青训营】后端笔记整理-3 | Go语言工程实践之测试
**本文由博主本人整理自第六届字节跳动青训营(后端组),首发于稀土掘金:🔗Go语言工程实践之测试 | 青训营 目录 一、概述 1、回归测试 2、集成测试 3、单元测试 二、单元测试 1、流程 2、规则 3、单元测试的例…...

【Android】Recyclerview的缓存复用
介绍 RecyclerView是Android开发中常用的一个高度可定制的列表视图组件。它是在ListView和GridView的基础上进行了改进和增强,旨在提供更好的性能和更灵活的布局管理。 RecyclerView的主要特点如下: 灵活的布局管理器(LayoutManager&#…...
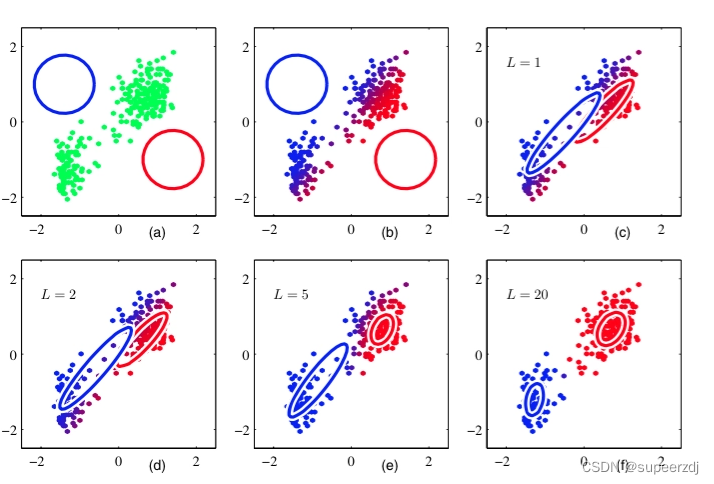
机器学习:混合高斯聚类GMM(求聚类标签)+PCA降维(3维降2维)习题
使用混合高斯模型 GMM,计算如下数据点的聚类过程: Datanp.array([1,2,6,7]) 均值初值为: μ1,μ21,5 权重初值为: w1,w20.5,0.5 方差: std1,std21,1 K2 10 次迭代后数据的聚类标签是多少? 采用python代码实现: from scipy import…...

libuv库学习笔记-processes
Processes libuv提供了相当多的子进程管理函数,并且是跨平台的,还允许使用stream,或者说pipe完成进程间通信。 在UNIX中有一个共识,就是进程只做一件事,并把它做好。因此,进程通常通过创建子进程来完成不…...

c++ 给无名形参提供默认值
如上图,若函数的形参不在函数体里使用,可以不提供形参名,而且可以给此形参提供默认值。也能编译通过。 在看vs2019上的源码时,也出现了这种写法。应用SFINAE(substitute false is not an error)原则&#x…...
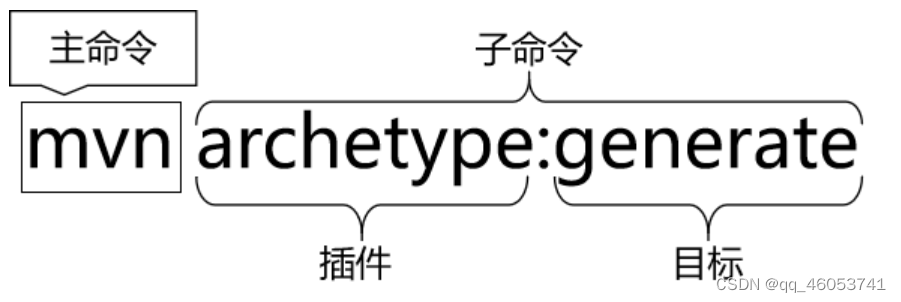
NO1.使用命令行创建Maven工程
①在工作空间目录下打开命令窗口 ②使用命令行生成Maven工程 mvn archetype:generate 运行 MVN 原型:生成命令,下面根据提示操作 选择一个数字或应用过滤器(格式:[groupId:]artifactId,区分大小写包含)&a…...

深度学习入门(一):神经网络基础
一、深度学习概念 1、定义 通过训练多层网络结构对位置数据进行分类或回归,深度学习解决特征工程问题。 2、深度学习应用 图像处理语言识别自然语言处理 在移动端不太好,计算量太大了,速度可能会慢 eg.医学应用、自动上色 3、例子 使用…...
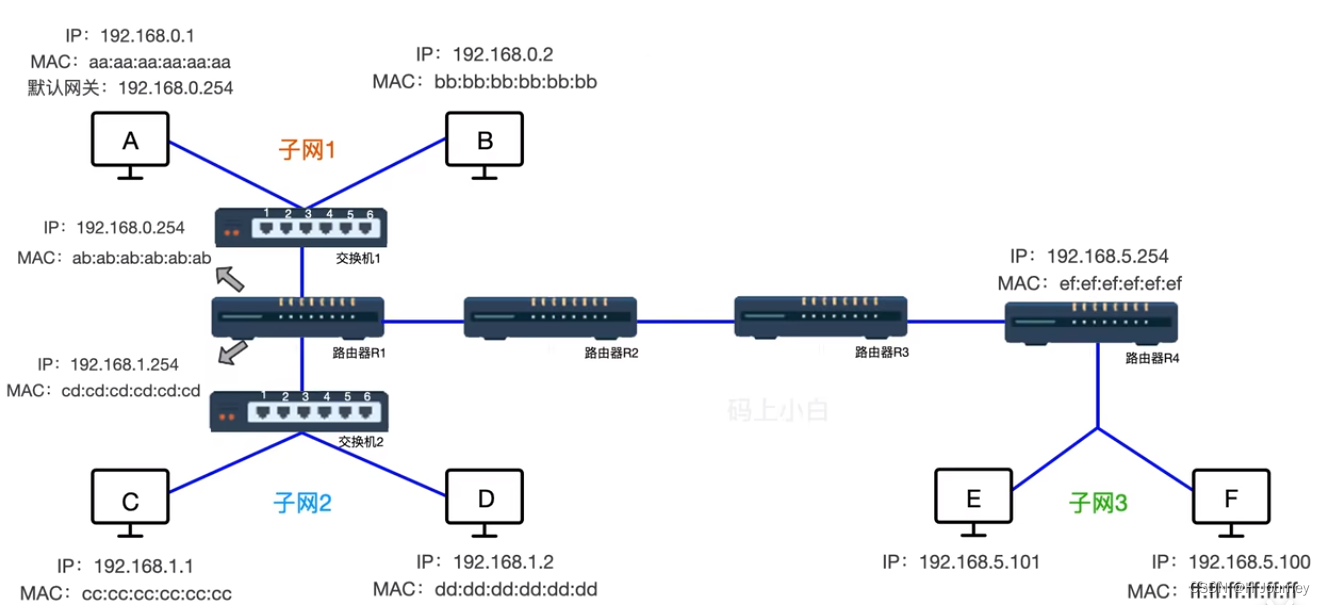
网络知识整理
网络知识整理 网络拓扑网关默认网关 数据传输拓扑结构层面协议层面 网络拓扑 网关 连接两个不同的网络的设备都可以叫网关设备,网关的作用就是实现两个网络之间进行通讯与控制。 网关设备可以是交换机(三层及以上才能跨网络) 、路由器、启用了路由协议的服务器、代…...

如何有效地使用ChatGPT写小说讲故事?
构思故事情节,虽有趣但耗时,容易陷入写作瓶颈。ChatGPT可提供灵感,帮你解决写作难题。要写出引人入胜的故事,关键在于抓住八个要素——主题、人物、视角、背景、情节、语气、冲突和解决办法。 直接给出故事模板,你可…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
