【数据结构】这堆是什么
目录
1.二叉树的顺序结构
2.堆的概念及结构
3.堆的实现
3.1 向上调整算法与向下调整算法
3.2 堆的创建
3.3 建堆的空间复杂度
3.4 堆的插入
3.5 堆的删除
3.6 堆的代码的实现
4.堆的应用
4.1 堆排序
4.2 TOP-K问题
首先,堆是一种数据结构,一种特殊的完全二叉树,采用顺序结构存储,在学习堆之前,我们先学习一下二叉树的顺序结构,再开始学习本篇文章的重点 --- 堆。
1.二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
完全二叉树的顺序存储:

非完全二叉树的顺序存储:
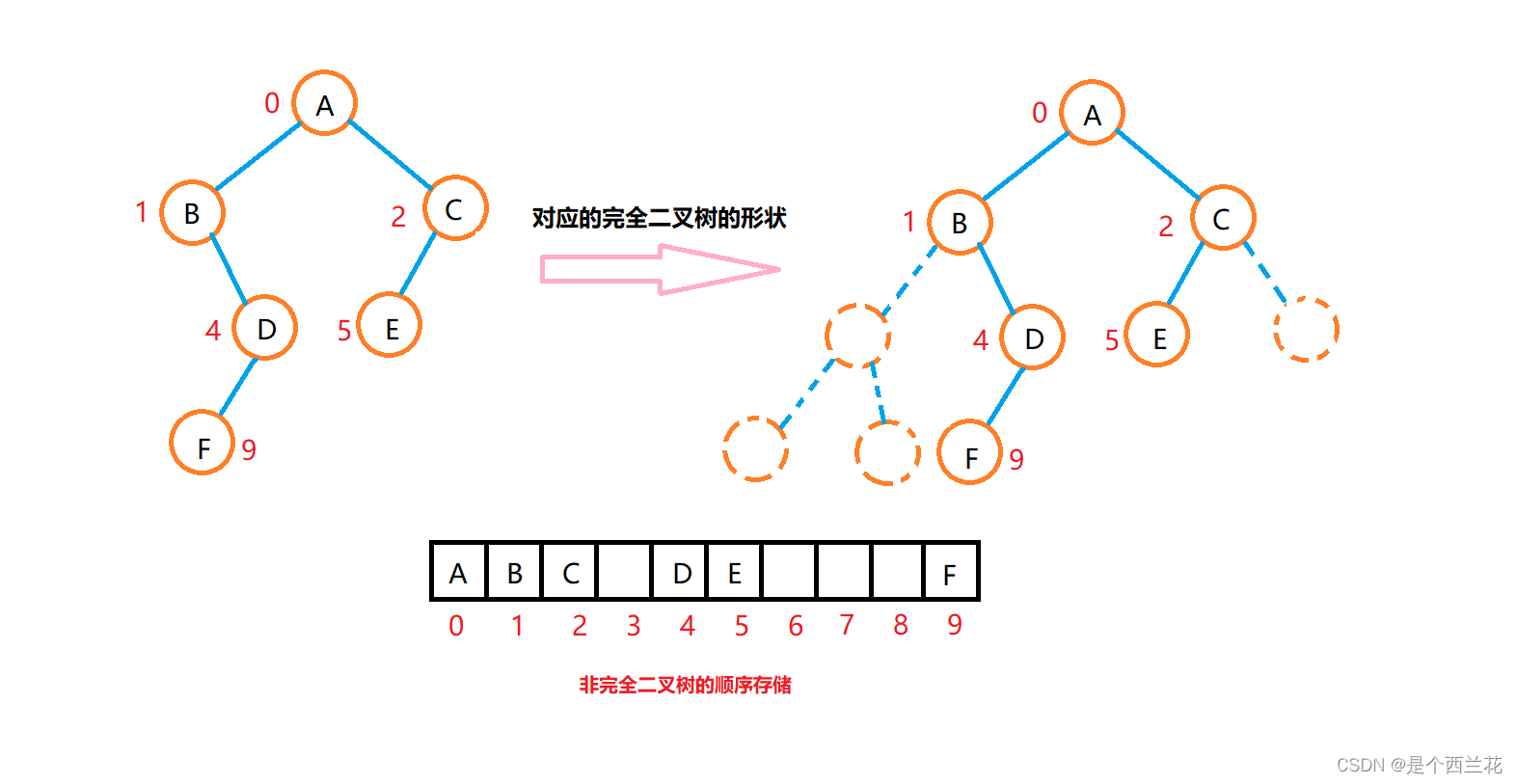 可以发现非完全二叉树可能会存在大量的空间浪费。
可以发现非完全二叉树可能会存在大量的空间浪费。
2.堆的概念及结构
如果有一个关键码的集合K= { k0,k1, k2,...,k(n-1) },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: Ki <= K(2i+1) 且 Ki <= K(2i+2) (Ki >= K(2i+1) 且 Ki >= K(2i+2) ) i =0,1,2...,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
概括来说:
堆有大根堆小根堆之分,简称大堆小堆:
大堆:堆内所有父节点都大于子节点。根节点最大。
小堆:堆内所有父节点都小于子节点。根节点最小。
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
示例:

例题:
1.下列关键字序列为堆的是:()
A 100,60,70,50,32,65
B 60,70,65,50,32,100C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
答案A
3.堆的实现
3.1 向上调整算法与向下调整算法
建堆有两种算法,一种是向上调整算法,一种是向下调整算法。现在我们给出一个数组,逻辑上看做一颗完全二叉树。
向上调整算法:
前提:前面元素已经构成堆,才能调整。
比如在下面小堆后面插入5

会将插入的数据向上调整到合适的位置
代码实现:
//交换
void Swap(HeapDataType* p1, HeapDataType* p2)
{HeapDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//小堆
void AdjustUp(HeapDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){if (arr[child] < arr[parent]){//交换Swap(&arr[child],&arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}建立大堆和小堆的向上调整算法判断条件不同,略有差异。
向下调整算法:
我们通过从根节点开始的向下调整算法,可以把它调整成一个小堆。
向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
int array[] = {27,15,19,18,28,34,65,49,25,37};以27为根的左右子树,都满足小堆的性质,只有根节点不满足,因此只需将根节点往下调整到合适的位置即可形成堆

代码实现
//向下调整
//完全二叉树没有左孩子,肯定没有右孩子 n是数组元素个数
void AdjustDown(HeapDataType* arr, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//找出左右孩子中最小的if (child + 1 < n && arr[child] > arr[child + 1]){child++;}if (arr[child] < arr[parent]){//交换Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
3.2 堆的创建
这里用向下调整算法创建,因为向上调整法时间复杂度较大,后面会讲
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算法,把它构建成一个堆。根节点左右子树不是堆,我们怎么调整呢?这里我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。
int a[] = {1,5,3,8,7,6};步骤如下:
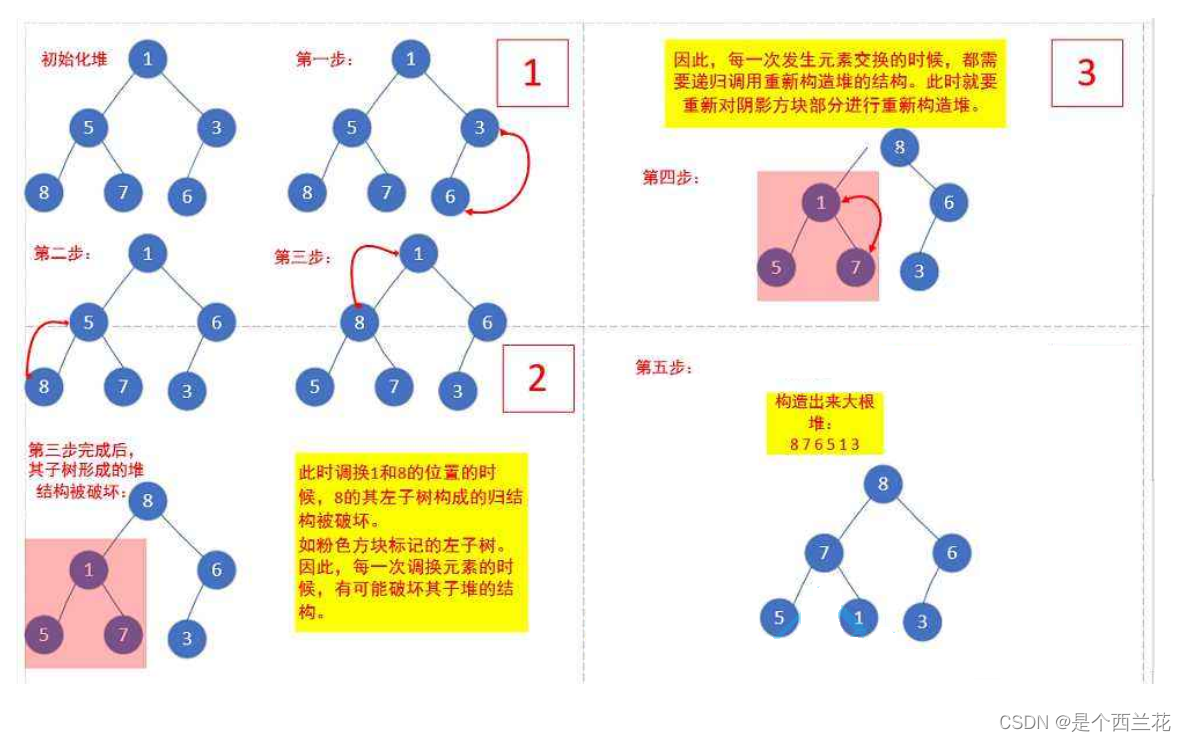
3.3 建堆的空间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):
向下调整算法建堆:

所以向下调整算法建堆的时间复杂度为O(N)。
向上调整算法建堆:
向上调整算法需要从第2个节点开始向上调整,调整好之后,第3个节点向上调整,依次向后,直到调完。

所以向上调整算法建堆的时间复杂度为O(N*(logN))。
所以这里推荐使用向下调整算法。
3.4 堆的插入
先插入一个10到数组的尾上,再进行向上调整算法,直到满足堆。
3.5 堆的删除
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。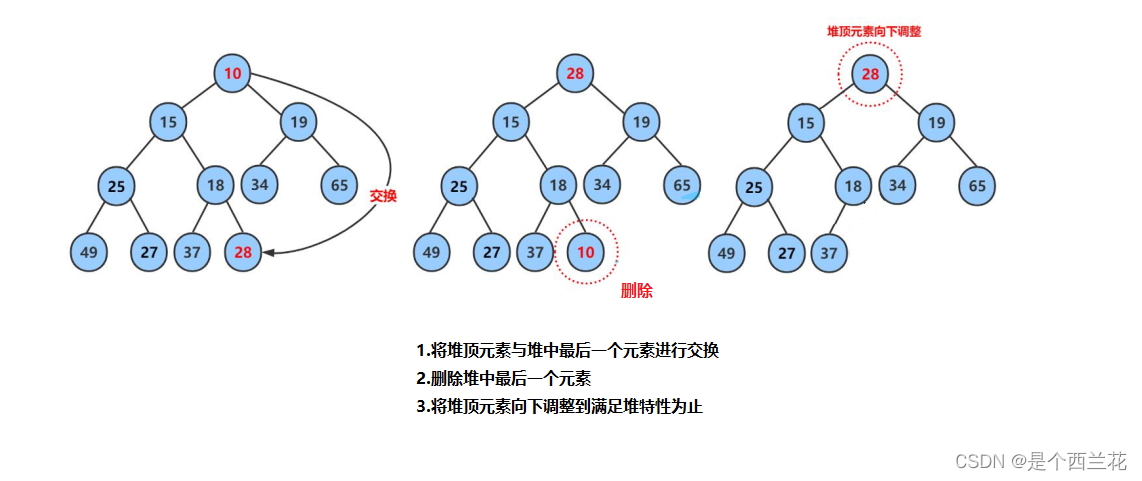
3.6 堆的代码的实现
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}Heap;// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);具体实现:
//交换元素
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType t = *p1;*p1 = *p2;*p2 = t;
}
//向下调整 小堆
void AdjustDown(HPDataType* arr, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//找最小子树if (child + 1 < n && arr[child] > arr[child + 1]){child++;}if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{return;}}
}
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{assert(hp);hp->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (hp->a == NULL){return;}hp->capacity = n;hp->size = n;for (int i = 0; i < n; i++){hp->a[i] = a[i];}for (int i = (n-1-1)/2; i >= 0; i--){AdjustDown(hp->a, n, i);}}
// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->size = hp->capacity = 0;
}//向上调整 小堆
void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else{return;}}
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);if (hp->size == hp->capacity){int newcapacity = hp->a == NULL ? 4 : hp->capacity * 2;HPDataType* ptr = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);if (ptr == NULL){perror("realloc fail");return;}hp->a = ptr;hp->capacity = newcapacity;}hp->a[hp->size] = x;hp->size++;//向上调整AdjustUp(hp->a, hp->size - 1);
}// 堆的删除
void HeapPop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));Swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;//向下调整AdjustDown(hp->a, hp->size, 0);}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);assert(!HeapEmpty(hp));return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->size;
}
// 堆的判空
int HeapEmpty(Heap* hp)
{assert(hp);return hp->size == 0;
}
4.堆的应用
4.1 堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
1.建堆
- 升序:建大堆
- 降序:建小堆
2.利用堆删除思想来进行排序。
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。
示例:升序:
#include<stdio.h>
//交换
void swap(int* p1, int* p2)
{int t = *p1;*p1 = *p2;*p2 = t;
}//向下调整 大堆
void Adjustdown(int* arr, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && arr[child] < arr[child + 1]){child++;}if (arr[child] > arr[parent]){swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapSort(int* a, int n)
{//建堆 升序建大堆//向下调整for (int i = (n - 1 - 1) / 2; i >= 0; i--){Adjustdown(a, n, i);}//排序 int end = n - 1;while (end){swap(&a[end], &a[0]);Adjustdown(a, end, 0);end--;}
}int main()
{int arr[] = { 10,50,40,20,30,60,70 };int sz = sizeof(arr) / sizeof(int);HeapSort(arr, sz);for (int i = 0; i < sz; i++){printf("%d ", arr[i]);}return 0;
}4.2 TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1.用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
2.用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素,再向下调整。
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
示例代码:这里需要生成文件后打开文件把几个数改成较大的值,模拟数据中的最大值,再注释掉CreateNDate()函数,模拟TOP-K问题,因为再写文件会把原来的数据覆盖掉。
#include<stdio.h>
#include<time.h>
void swap(int* p1, int* p2)
{int t = *p1;*p1 = *p2;*p2 = t;
}//小堆
void Adjustdown(int* arr, int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && arr[child] > arr[child + 1]){child++;}if (arr[child] < arr[parent]){swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void CreateNDate()
{// 造数据int n = 10000;srand((unsigned int)time(NULL));FILE* file = fopen("data.txt", "w");for (int i = 0; i < n; i++){fprintf(file,"%d\n", rand() % 10000);//生成10000以内的随机数}fclose(file);
}void PrintTopK(int k)//最大的k个数
{CreateNDate();//造数据,选这些数据中的最大值FILE* file = fopen("data.txt", "r");//建立小堆int* arr = (int*)malloc(sizeof(int) * k);for (int i = 0; i < k; i++){fscanf(file, "%d", &arr[i]);}for (int i = (k-1-1)/2; i >=0 ; i--){Adjustdown(arr, k, i);}int a = 0;while (fscanf(file, "%d", &a)!=EOF){if (arr[0] < a){swap(&arr[0], &a);}Adjustdown(arr, k, 0);}for (int i = 0; i < k; i++){printf("%d ", arr[i]);}fclose(file);free(arr);
}int main()
{PrintTopK(5);return 0;
}
本篇结束
相关文章:

【数据结构】这堆是什么
目录 1.二叉树的顺序结构 2.堆的概念及结构 3.堆的实现 3.1 向上调整算法与向下调整算法 3.2 堆的创建 3.3 建堆的空间复杂度 3.4 堆的插入 3.5 堆的删除 3.6 堆的代码的实现 4.堆的应用 4.1 堆排序 4.2 TOP-K问题 首先,堆是一种数据结构,一种特…...
FFmpeg 音视频开发工具
目录 FFmpeg 下载与安装 ffmpeg 使用快速入门 ffplay 使用快速入门 FFmpeg 全套下载与安装 1、FFmpeg 是处理音频、视频、字幕和相关元数据等多媒体内容的库和工具的集合。一个完整的跨平台解决方案,用于录制、转换和流式传输音频和视频。 官网:http…...

Go 语言 select 都能做什么?
原文链接: Go 语言 select 都能做什么? 在 Go 语言中,select 是一个关键字,用于监听和 channel 有关的 IO 操作。 通过 select 语句,我们可以同时监听多个 channel,并在其中任意一个 channel 就绪时进行相…...
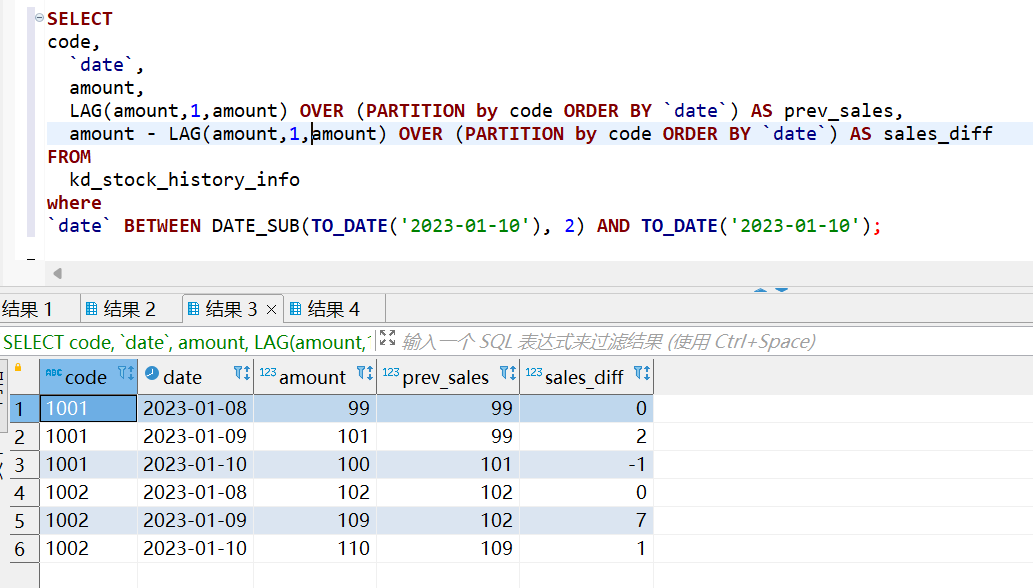
Hive之窗口函数lag()/lead()
一、函数介绍 lag()与lead函数是跟偏移量相关的两个分析函数 通过这两个函数可以在一次查询中取出同一字段的前N行的数据(lag)和后N行的数据(lead)作为独立的列,从而更方便地进行进行数据过滤,该操作可代替表的自联接,且效率更高 lag()/lead() lag(c…...

Vite+Typescript+Vue3学习笔记
ViteTypescriptVue3学习笔记 1、项目搭建 1.1、创建项目(yarn) D:\WebstromProject>yarn create vite yarn create v1.22.19 [1/4] Resolving packages... [2/4] Fetching packages... [3/4] Linking dependencies... [4/4] Building fresh packages...success Installed…...
二、SQL-6.DCL-2).权限控制
*是数据库和表的通配符,出现在数据库位置上表示所有数据库,出现在表名位置上,表示所有表 %是主机名的通配符,表示所有主机。 e.g.所有数据库(*)的所有表(*)的所有权限(a…...

[OpenStack] GPU透传
GPU透传本质就是PCI设备透传,不算是什么新技术。之前按照网上方法都没啥问题,但是这次测试NVIDIA A100遇到坑了。 首先是禁用nouveau 把intel_iommuon rdblacklistnouveau写入/etc/default/grub的cmdline,然后grub2-mkconfig -o /etc/grub2.c…...

无涯教程-jQuery - Progressbar组件函数
小部件进度条功能可与JqueryUI中的小部件一起使用。一个简单的进度条显示有关进度的信息。一个简单的进度条如下所示。 Progressbar - 语法 $( "#progressbar" ).progressbar({value: 37 }); Progressbar - 示例 以下是显示进度条用法的简单示例- <!doctype …...

[SQL挖掘机] - 窗口函数 - rank
介绍: rank() 是一种常用的窗口函数,它为结果集中的每一行分配一个排名(rank)。这个排名基于指定的排序顺序,并且在遇到相同的值时,会跳过相同的排名。 用法: rank() 函数的语法如下: rank() over ([pa…...

VBAC多层防火墙技术的研究-状态检测
黑客技术的提升和黑客工具的泛滥,造成大量的企业、机构和个人的电脑系统遭受程度不同的入侵和攻击,或面临随时被攻击的危险。迫使大家不得不加强对自身电脑网络系统的安全防护,根据系统管理者设定的安全规则把守企业网络,提供强大的、应用选通、信息过滤、流量控制、网络侦…...
PHP8的数据类型-PHP8知识详解
在PHP8中,变量不需要事先声明,赋值即声明。 不同的数据类型其实就是所储存数据的不同种类。在PHP8.0、8.1中都有所增加。以下是PHP8的15种数据类型: 1、字符串(String):用于存储文本数据,可以使…...

明晚直播:可重构计算芯片的AI创新应用分享!
大模型技术的不断升级及应用落地,正在推动人工智能技术发展进入新的阶段,而智能化快速增长和发展的市场对芯片提出了更高的要求:高算力、高性能、灵活性、安全性。可重构计算区别于传统CPU、GPU,以指令驱动的串行执行方式…...
flask 点赞系统
dianzan.html页面 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>点赞系统</title> </head> <body><h2>这是一个点赞系统</h2><table border"1"><…...
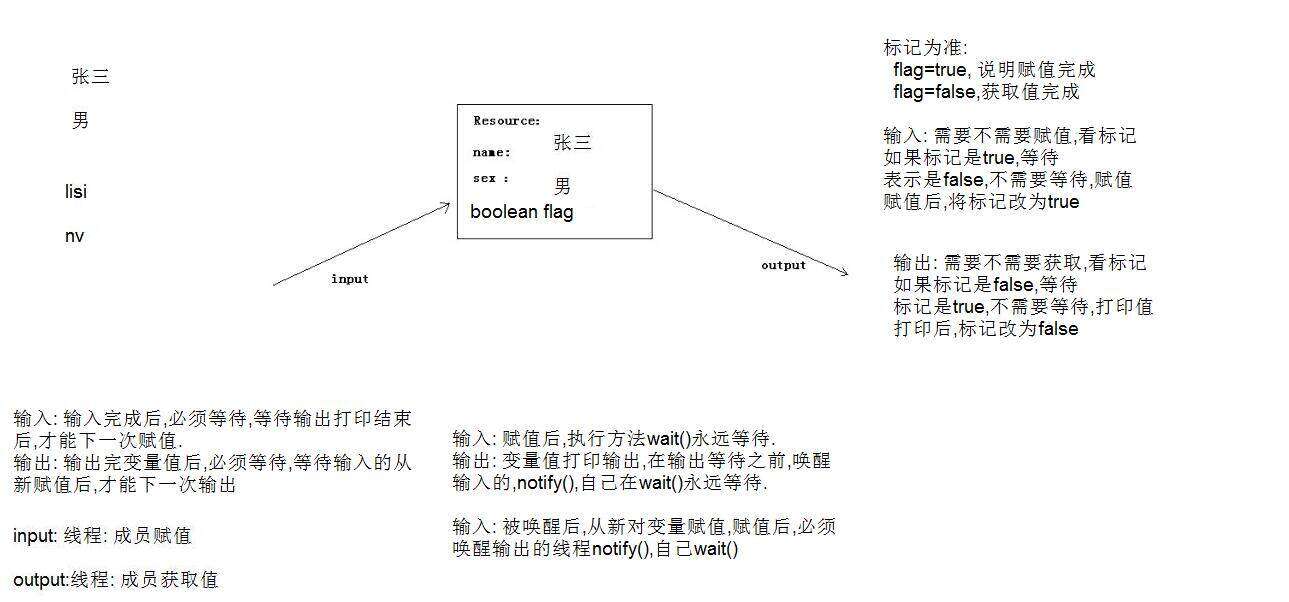
关于Java的多线程实现
多线程介绍 进程:进程指正在运行的程序。确切的来说,当一个程序进入内存运行,即变成一个进程,进程是处于运行过程中的程序,并且具有一定独立功能。 线程:线程是进程中的一个执行单元,负责当前进…...

如何判断某个视频是深度伪造的?
目录 一、前言 二、仔细检查面部动作 三、声音可以提供线索 四、观察视频中人物的身体姿势 五、小心无意义的词语 深造伪造危险吗? 一、前言 制作深度伪造视频就像在Word文档中编辑文本一样简单。换句话说,您可以拍下任何人的视频,让他…...

ESP32(MicroPython) 四足机器人(一)
最近决定研究一下四足机器人,但市面上的产品,要么性价比低,要么性能达不到要求。本人就另外买了零件,安装到之前的一个麦克纳姆轮底盘的底板上。(轮子作为装饰,使用铜柱固定) 舵机使用MG996R&a…...
力扣刷题记录---利用python实现链表的基本操作
文章目录 前言一、利用python实现链表的基本操作1.节点的定义使用类实现:1.链表的定义使用类实现:3.判断是否为空函数实现:4.链表长度函数实现:5.遍历链表函数实现:6.头插法函数实现:7.尾插法函数实现&…...

OpenAI重磅官宣ChatGPT安卓版本周发布,现已开启下载预约,附详细预约教程
7月22号,OpenAI 突然宣布,安卓版 ChatGPT 将在下周发布!换句话说,本周安卓版 ChatGPT正式上线! 最早,ChatGPT仅有网页版。 今年5月,iOS版ChatGPT正式发布,当时OpenAI表示Android版将…...
整理汇总)
PHP 支付宝支付、订阅支付(周期扣款)整理汇总
最近项目中需要使用支付宝的周期扣款,整理一下各种封装方法 APP支付(服务端) /******************************************************* 调用方法******************************************************/function test_pay(){$isSubscri…...

python-pytorch基础之神经网络回归
这里写目录标题 定义数据集定义函数生成数据集 使用Dataloader加载dataset定义神经网络定义实例化查看是否是输出的一个 训练编写trian方法训练并保存模型 测试模型结果构造数据测试结论 定义数据集 import torch import random定义函数 # 生成数据 def get_rancledata():wid…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
