数学建模学习(7):单目标和多目标规划
优化问题描述

优化
优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值

线性规划
线性规划是指目标函数和约束都是线性的情况
[x,fval]=linprog(f,A,b,Aeq,Beq,LB,UB)
x:求得最优情况下变量的解
fval:求得最优目标值
f:目标函数的系数(符号按最小值标准,若目标是求解机大值可以通过添加负号改成求极小值)
A:不等式约束的变量系数(符合按小于标准,如果是大于约束可通过加负号变成小于)
b:不等式约束的常量
Aeq:等式约束的变量系数Beq:等式约束的常量LB:变量的下限UB:变量的上限

%% 线性规划
clc;clear;close all;
%目标函数/max 要改成min 的形式,max最大值可以系数加个负号的变成求min
f=[-1;-2;3]; %不等约束 /化成标准形式 x1+x2<=
% -x1-x2+0*x3<=-3
%0*x1-x2-x3<=-3
A=[-1,-1,0;0,-1,-1];%左边特征矩阵
b=[-3;-3]; %右边%等式约束
Aeq=[1,0,1];
Beq=[4];%变量约束,上限,下限
LB=zeros(3,1);
UB=2*ones(3,1);%优化
[x,fval]=linprog(f,A,b,Aeq,Beq,LB,UB);
%
objstr=['目标函数最优值:',num2str(fval)];
disp(objstr)
for i=1:length(x)xstr=['x',num2str(i),'的值为:',num2str(x(i))];disp(xstr)
end非线性规划
非线性规划是指目标函数和约束有非线性的情况

%% 非线性规划1
clc;clear;close all;
%初始解,随意给个初始解
x0=zeros(3,1);%不等约束
A=[2,1,3];%左边特征矩阵
b=[6]; %右边%描述线性
%等式约束
Aeq=[];
Beq=[];%变量约束,上限,下限
LB=zeros(3,1);
UB=1*ones(3,1);%
%优化求解 max 加负号
fun = @(x)-x(1)^2+x(2)^2-x(2)*x(3);
%
nonlcon = @unitdisk;
[x,fval]=fmincon(fun,x0,A,b,Aeq,Beq,LB,UB,nonlcon);objstr=['目标函数最优值:',num2str(-fval)];%num2str 数字变成字符
disp(objstr)
for i=1:length(x)xstr=['x',num2str(i),'的值为:',num2str(x(i))];disp(xstr)
endfunction [c,ceq] = unitdisk(x)
%c为不等式非线性约束
%ceq为等式非线性约束
c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;
%多个非线性约束的话,可以用[约束1;约束2];
ceq = [];
end%%
%遇到较为复杂的目标函数
%可以写为函数的形式
fun = @obj;
function y = obj(x)y1 = x(1)^2+x(2)^2;y = sqrt(y1)+x(3)^3;
end
%%多目标优化

多目标求解的第一种方法:
%% 非线性规划1
clc;clear;close all;
%%
%初始解,随意给个初始解
x0=zeros(3,1);%不等约束
A=[2,1,3];%左边特征矩阵
b=[6]; %右边%等式约束
Aeq=[];
Beq=[];%变量约束,上限,下限
LB=zeros(3,1);
UB=1*ones(3,1);
%优化求解
%%
w1=0.5;w2=0.5;
fun = @(x)(-x(1)^2+x(2)^2-x(2)*x(3))*w1+(2*x(1)^2-x(2)^3+2*x(2)*x(3))*w2;nonlcon = @unitdisk;
[x1,fval1]=fmincon(fun,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval1)];
disp(objstr)
for i=1:length(x1)xstr=['x',num2str(i),'的值为:',num2str(x1(i))];disp(xstr)
endfunction [c,ceq] = unitdisk(x)
%c为不等式非线性约束
%ceq为等式非线性约束
c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;
ceq = [];
end
多目标求解的第二种方法
%% 非线性规划1
clc;clear;close all;
%%
%初始解,随意给个初始解
x0=zeros(3,1);%不等约束
A=[2,1,3];%左边特征矩阵
b=[6]; %右边%等式约束
Aeq=[];
Beq=[];%变量约束,上限,下限
LB=zeros(3,1);
UB=1*ones(3,1);
%优化求解
%%
fun1 = @(x)-x(1)^2+x(2)^2-x(2)*x(3);
fun2 = @(x)2*x(1)^2-x(2)^3+2*x(2)*x(3);
%%
nonlcon = @unitdisk;
[x1,fval1]=fmincon(fun1,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval1)];
disp(objstr)
for i=1:length(x1)xstr=['x',num2str(i),'的值为:',num2str(x1(i))];disp(xstr)
end
[x2,fval2]=fmincon(fun2,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval2)];
disp(objstr)
for i=1:length(x2)xstr=['x',num2str(i),'的值为:',num2str(x2(i))];disp(xstr)
end
%% 多目标规划
goal=[fval1,fval2];
func = @(x)[-x(1)^2+x(2)^2-x(2)*x(3);2*x(1)^2-x(2)^3+2*x(2)*x(3)];
weight=[1,1];
[x,fival]=fgoalattain(func,x0,goal,weight,A,b,Aeq,Beq,LB,UB,nonlcon);
disp('在两个目标的优化结果为')
disp(func(x))
for i=1:length(x)xstr=['x',num2str(i),'的值为:',num2str(x(i))];disp(xstr)
end
%%
function [c,ceq] = unitdisk(x)
%c为不等式非线性约束
%ceq为等式非线性约束
c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;
ceq = [];
end
%% 非线性规划1
clc;clear;close all;
%%
%初始解,随意给个初始解
x0=zeros(10,1);%不等约束
A=[];%左边特征矩阵
b=[]; %右边%等式约束
Aeq=[];
Beq=[];%变量约束,上限,下限
LB=-1*ones(10,1);LB(1)=0;
UB=1*ones(10,1);
%优化求解
%%
fun1 = @obj1;
fun2 = @obj2;
%%
nonlcon = [];
[x1,fval1]=fmincon(fun1,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval1)];
disp(objstr)
for i=1:length(x1)xstr=['x',num2str(i),'的值为:',num2str(x1(i))];disp(xstr)
end
[x2,fval2]=fmincon(fun2,x0,A,b,Aeq,Beq,LB,UB,nonlcon);
objstr=['目标函数最优值:',num2str(fval2)];
disp(objstr)
for i=1:length(x2)xstr=['x',num2str(i),'的值为:',num2str(x2(i))];disp(xstr)
end
%% 多目标规划
goal=[fval1,fval2];
func = @obj3;
weight=[1,1];
[x,fival]=fgoalattain(func,x0,goal,weight,A,b,Aeq,Beq,LB,UB,nonlcon);
disp('在两个目标的优化结果为')
disp(func(x))
for i=1:length(x)xstr=['x',num2str(i),'的值为:',num2str(x(i))];disp(xstr)
end
%%
function y1=obj1(x)[dim, num] = size(x);tmp = zeros(dim,num);tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;tmp1 = sum(tmp(3:2:dim,:)); % odd indextmp2 = sum(tmp(2:2:dim,:)); % even indexy1 = x(1,:) + 2.0*tmp1/size(3:2:dim,2);
% y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);
end
function y2=obj2(x)[dim, num] = size(x);tmp = zeros(dim,num);tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;tmp1 = sum(tmp(3:2:dim,:)); % odd indextmp2 = sum(tmp(2:2:dim,:)); % even index
% y2 = x(1,:) + 2.0*tmp1/size(3:2:dim,2);y2 = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);
end
function y=obj3(x)[dim, num] = size(x);tmp = zeros(dim,num);tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;tmp1 = sum(tmp(3:2:dim,:)); % odd indextmp2 = sum(tmp(2:2:dim,:)); % even indexy(1,:) = x(1,:) + 2.0*tmp1/size(3:2:dim,2);y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);
end
% function [c,ceq] = unitdisk(x)
% %c为不等式非线性约束
% %ceq为等式非线性约束
% c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;
% ceq = [];
% end
相关文章:

数学建模学习(7):单目标和多目标规划
优化问题描述 优化 优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值 线性规划 线性规划是指目标函数和约束都是线性的情况 [x,fval]linprog(f,A,b,Aeq,Beq,LB,U…...

Element UI如何自定义样式
简介 Element UI是一套非常完善的前端组件库,但是如何个性化定制其中的组件样式呢?今天我们就来聊一聊这个 举例 就拿最常见的按钮el-button来举例,一般来说默认是蓝底白字。效果图如下 可是我们想个性化定制,让他成为粉底红字应…...

protobuf入门实践2
如何在proto中定义一个rpc服务? syntax "proto3"; //声明protobuf的版本package fixbug; //声明了代码所在的包 (对于C来说就是namespace)//下面的选项,表示生成service服务类和rpc方法描述, 默认是不生成的 option cc_generi…...

adb shell使用总结
文章目录 日志记录系统概览adb 使用方式 adb命令日志过滤按照告警等级进行过滤按照tag进行过滤根据告警等级和tag进行联合过滤屏蔽系统和其他App干扰,仅仅关注App自身日志 查看“当前页面”Activity文件传输截屏和录屏安装、卸载App启动activity其他 日志记录系统概…...
-Tag的含义、Tag类型与其他的转换)
UG NX二次开发(C++)-Tag的含义、Tag类型与其他的转换
文章目录 1、前言2、Tag号的含义3、tag_t转换为int3、TaggedObject与Tag转换3.1 TaggedObject定义3.2 TaggedObject获取Tag3.3 根据Tag获取TaggedObject4.Tag与double类型的转换1、前言 在UG NX中,每个对象对应一个tag号,C++中,其类型是tag_t,一般是5位或者6位的int数字,…...
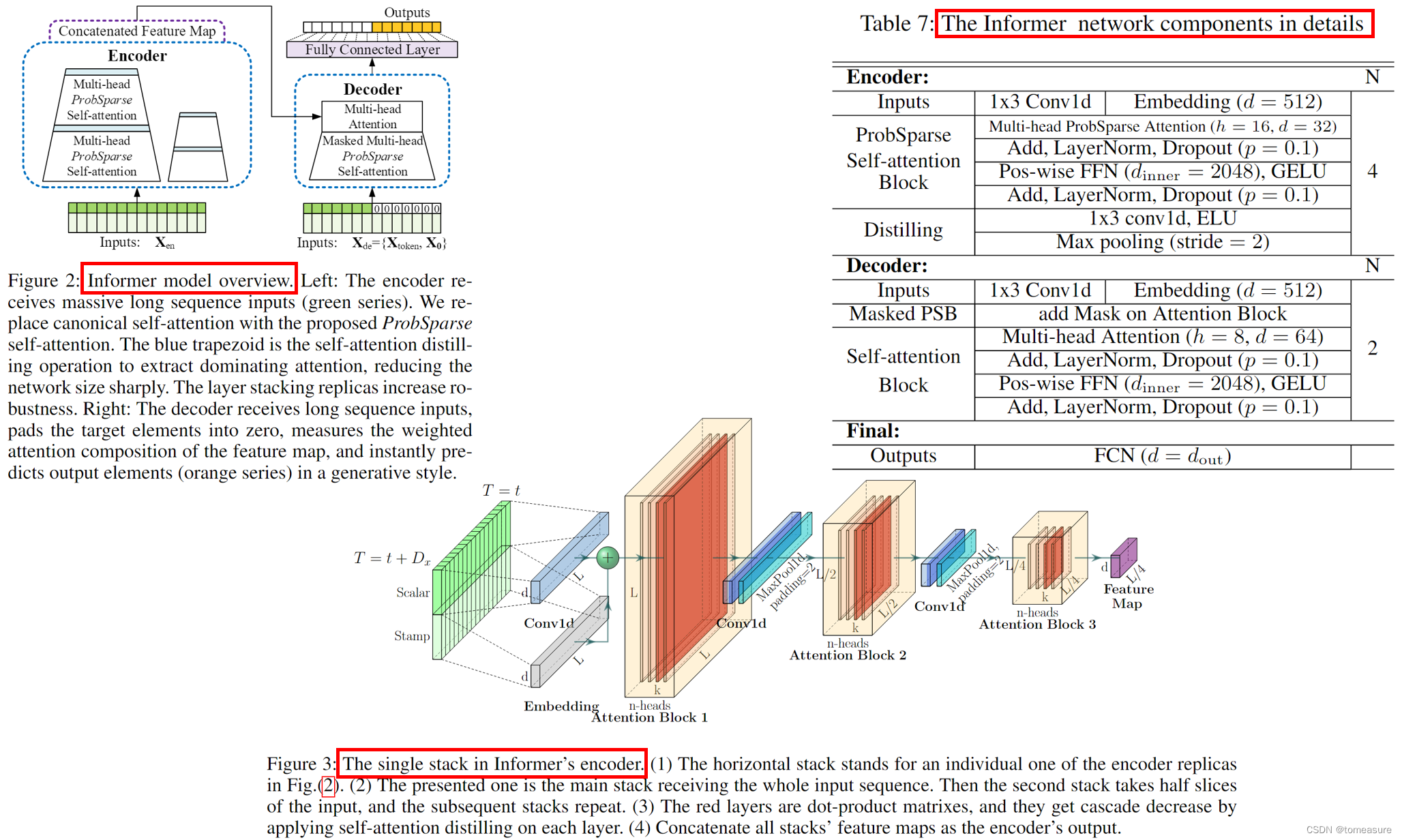
Informer 论文学习笔记
论文:《Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting》 代码:https://github.com/zhouhaoyi/Informer2020 地址:https://arxiv.org/abs/2012.07436v3 特点: 实现时间与空间复杂度为 O ( …...

c语言位段知识详解
本篇文章带来位段相关知识详细讲解! 如果您觉得文章不错,期待你的一键三连哦,你的鼓励是我创作的动力之源,让我们一起加油,一起奔跑,让我们顶峰相见!!! 目录 一.什么是…...
FFmpeg aresample_swr_opts的解析
ffmpeg option的解析 aresample_swr_opts是AVFilterGraph中的option。 static const AVOption filtergraph_options[] {{ "thread_type", "Allowed thread types", OFFSET(thread_type), AV_OPT_TYPE_FLAGS,{ .i64 AVFILTER_THREAD_SLICE }, 0, INT_MA…...

CAN学习笔记3:STM32 CAN控制器介绍
STM32 CAN控制器 1 概述 STM32 CAN控制器(bxCAN),支持CAN 2.0A 和 CAN 2.0B Active版本协议。CAN 2.0A 只能处理标准数据帧且扩展帧的内容会识别错误,而CAN 2.0B Active 可以处理标准数据帧和扩展数据帧。 2 bxCAN 特性 波特率…...

软工导论知识框架(二)结构化的需求分析
本章节涉及很多重要图表的制作,如ER图、数据流图、状态转换图、数据字典的书写等,对初学者来说比较生僻,本贴只介绍基础的轮廓,后面会有单独的帖子详解各图表如何绘制。 一.结构化的软件开发方法:结构化的分析、设计、…...

[SQL挖掘机] - 算术函数 - abs
介绍: 当谈到 SQL 中的 abs 函数时,它是一个用于计算数值的绝对值的函数。“abs” 代表 “absolute”(绝对),因此 abs 函数的作用是返回一个给定数值的非负值(即该数值的绝对值)。 abs 函数接受一个参数&a…...

vue拼接html点击事件不生效
vue使用ts,拼接html,点击事件不生效或者报 is not defined 点击事件要用onclick 不是click let data{name:测,id:123} let conHtml <div> "名称:" data.name "<br>" <p class"cursor blue&quo…...

【Spring】Spring之依赖注入源码解析
1 Spring注入方式 1.1 手动注入 xml中定义Bean,程序员手动给某个属性赋值。 set方式注入 <bean name"userService" class"com.firechou.service.UserService"><property name"orderService" ref"orderService"…...

【微软知识】微软相关技术知识分享
微软技术领域 一、微软操作系统: 微软的操作系统主要是 Windows 系列,包括 Windows 10、Windows Server 等。了解 Windows 操作系统的基本使用、配置和故障排除是非常重要的。微软操作系统(Microsoft System)是美国微软开发的Wi…...

12.python设计模式【观察者模式】
内容:定义对象间的一种一对多的依赖关系,当一个对象的状态发生改变的时候,所有依赖于它的对象得到通知并被自动更新。观者者模式又称为“发布-订阅”模式。比如天气预报,气象局分发气象数据。 角色: 抽象主题…...
重生之我要学C++第五天
这篇文章主要内容是构造函数的初始化列表以及运算符重载在顺序表中的简单应用,运算符重载实现自定义类型的流插入流提取。希望对大家有所帮助,点赞收藏评论,支持一下吧! 目录 构造函数进阶理解 1.内置类型成员在参数列表中的定义 …...

复习之linux高级存储管理
一、lvm----逻辑卷管理 1.lvm定义 LVM是 Logical Volume Manager(逻辑卷管理)的简写,它是Linux环境下对磁盘分区进行管理的一种机制。 逻辑卷管理器(LogicalVolumeManager)本质上是一个虚拟设备驱动,是在内核中块设备和物理设备…...
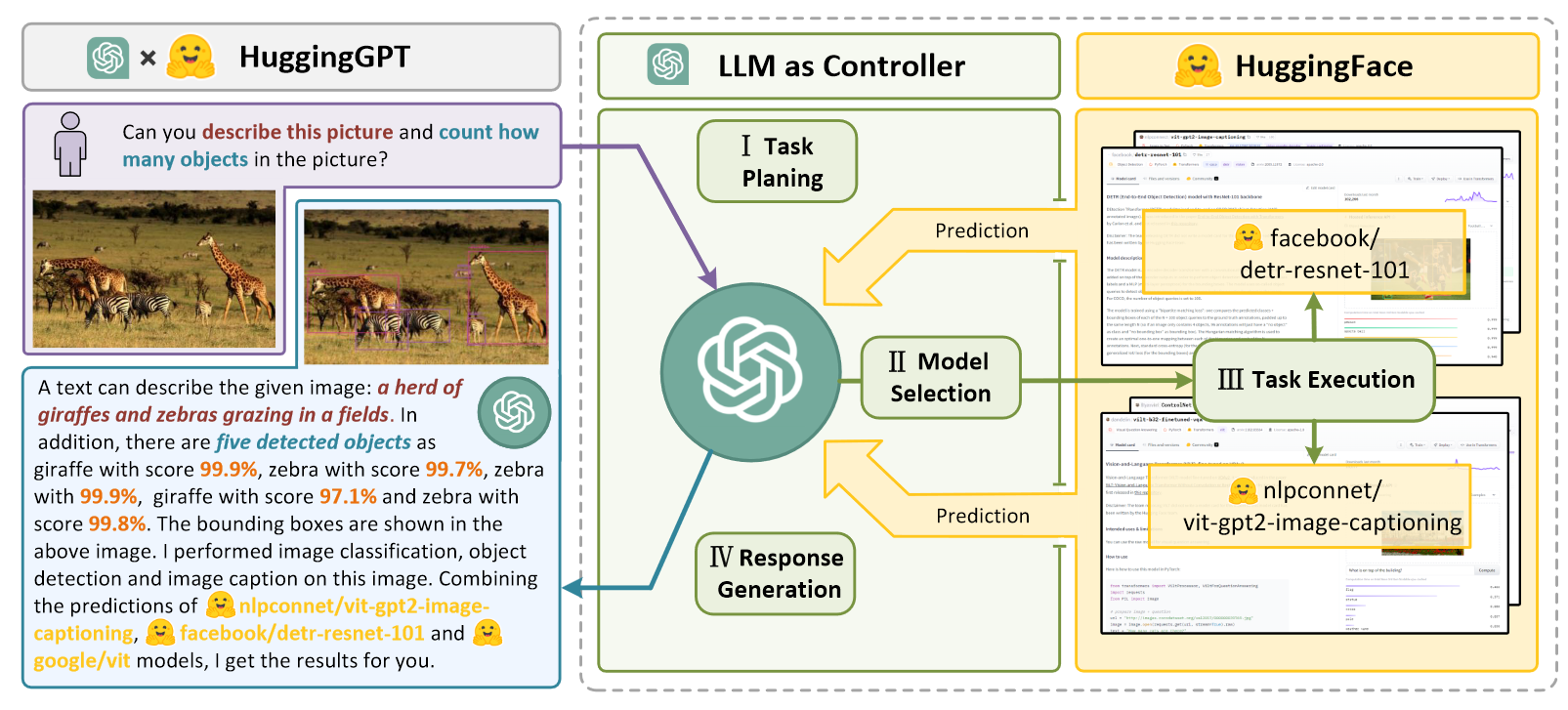
HuggingGPT Solving AI Tasks with ChatGPT and its Friends in Hugging Face
总述 HuggingGPT 让LLM发挥向路由器一样的作用,让LLM来选择调用那个专业的模型来执行任务。HuggingGPT搭建LLM和专业AI模型的桥梁。Language is a generic interface for LLMs to connect AI models 四个阶段 Task Planning: 将复杂的任务分解。但是这里…...

java工程重写jar包中class类覆盖问题
结论:直接在程序中复写jar中的类即可 原因:一般我java工程是运行在tomcat容器中,tomcat容易在加载我们工程类和jar包是的优先级为: 我们工程的class 先于 我们工程lib下的jar 重复的类只加载一次,加载我们复写后的类后…...

Mybatis基于注解与XML开发
文章目录 1 关于SpringBoot2 关于MyBatis2.1 MyBatis概述2.2 MyBatis核心思想2.3 MyBatis使用流程3 MyBatis配置SQL方式3.1 基于注解方式3.1.1 说明3.1.2 使用流程3.1.3 常用注解 3.2 基于XML方式3.2.1 相比注解优势3.2.2 使用流程3.2.3 常用标签 1 关于SpringBoot SpringBoot…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...


