matlab使用教程(5)—矩阵定义和基本运算
1创建矩阵
A = pascal(3)B = magic(3)C = randi(10,3,2)u = [3; 1; 4]
v = [2 0 -1]
s = 72矩阵的加法和减法
X = A + B
Y = X - A3向量乘积和转置
u = [3; 1; 4];
v = [2 0 -1];
x = v*uX = u*vB = magic(3)X = B'x = v'z = [1+2i 7-3i 3+4i; 6-2i 9i 4+7i]z'z.'4矩阵乘法
A = pascal(3);
B = magic(3);
m = 3;
n = 3;
for i = 1:m
for j = 1:n
C(i,j) = A(i,:)*B(:,j);
end
endX = A*B
Y = B*Au = [3; 1; 4];
x = A*u
v = [2 0 -1];
y = v*BX = A*CY = C*As = 10;
w = s*y5单位矩阵
eye(m,n)6矩阵求逆
A = pascal(3)X = inv(A)A*Xd = det(A)c = cond(A)7向量范数和矩阵范数

v = [2 0 -1];
[norm(v,1) norm(v) norm(v,inf)]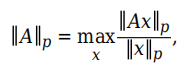
A = pascal(3);
[norm(A,1) norm(A) norm(A,inf)]vecnorm(A)8使用线性代数方程函数的多线程计算
相关文章:
matlab使用教程(5)—矩阵定义和基本运算
本博客介绍如何在 MATLAB 中创建矩阵和执行基本矩阵计算。 MATLAB 环境使用矩阵来表示包含以二维网格排列的实数或复数的变量。更广泛而言,数组为向量、矩阵或更高维度的数值网格。MATLAB 中的所有数组都是矩形,在这种意义上沿任何维度的分量向量的长度…...

用HTML写一个简单的静态购物网站
实现代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>购物网站</title> &l…...

如何在go中实现程序的优雅退出,go-kratos源码解析
使用kratos这个框架有近一年了,最近了解了一下kratos关于程序优雅退出的具体实现。 这部分逻辑在app.go文件中,在main中,找到app.Run方法,点进入就可以了 它包含以下几个部分: App结构体:包含应用程序的配置选项和运行时状态。 …...

Appium+python自动化(二十八)- 高级滑动(超详解)
高级溜冰的滑动 滑动操作一般是两点之间的滑动,这种滑动在这里称其为低级的溜冰滑动;就是上一节给小伙伴们分享的。然而实际使用过程中用户可能要进行一些多点连续滑动操作。如九宫格滑动操作,连续拖动图片移动等场景。那么这种高级绚丽的溜…...
github token使用方法
git remote set-url origin https://<githubtoken>github.com/<username>/<repositoryname>.git 在私有仓库的HTTPS的url上加入<githubtoken>即为token url,可以免ssh key登录...

Spring属性注解对配置项名称的自动转换
一、前言 在Spring中,我们经常需要将配置文件中的属性值注入到Java类中。Spring提供了两个主要的注解来实现这一功能:Value 和 ConfigurationProperties。其中 ConfigurationProperties支持将配置项名称与Java类中的属性名进行自动转换,包括…...
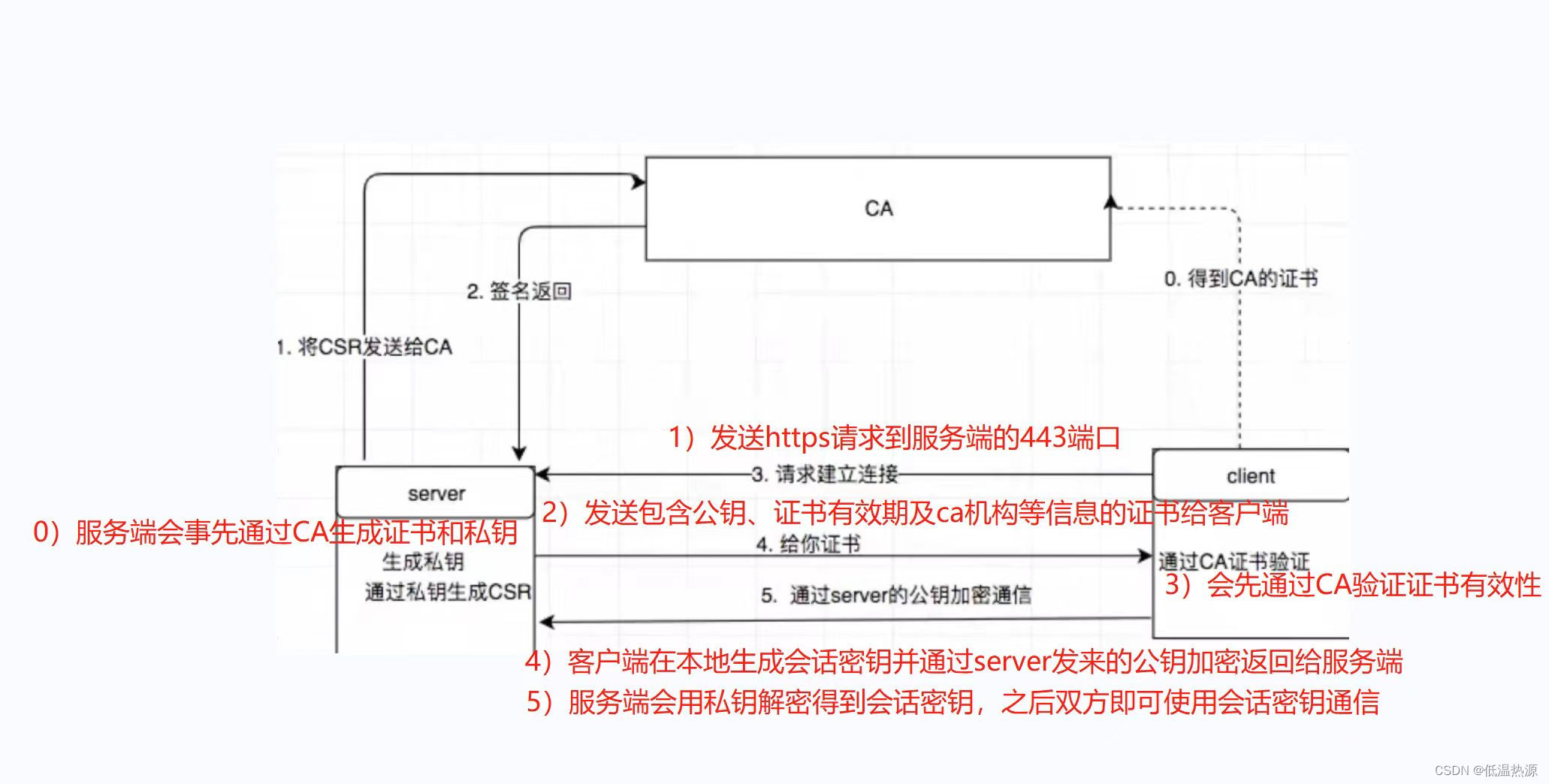
Docker 安全 Docker HTTPS请求过程与配置
Docker 容器安全注意点 尽量别做的事 尽量不用 --privileged 运行容器(授权容器root用户拥有宿主机的root权限) 尽量不用 --network host 运行容器(使用 host 网络模式共享宿主机的网络命名空间) 尽量不在容器中运行 ssh 服务 尽…...
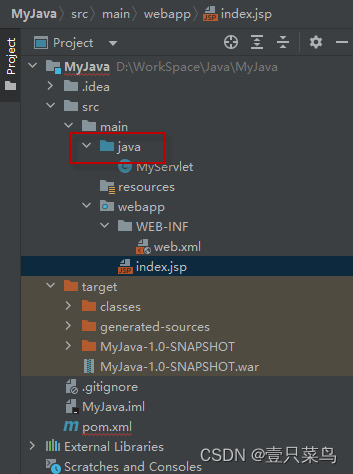
DevOps(三)
CD(二) 1. 整体流程2. 环境准备1. jenkins安装2. 编译安装git3. docker安装4. docker-compose安装5. sonarqube安装6. harbor安装7. gitlab私服8. maven安装9. Nexus部署10. K8s部署3. 安装java及编写代码3.1 安装java3.2 安装IntelliJ IDEA3.3 安装tomcat3.4 安装maven3.5 c…...

AOP的妙用
一、改代码 自定义注解用于提示该代码已经在AOP中重构了 public interface ReviseToAop {// 用于记录修改状态String value() default ""; }使用注解(无意义,只是表名被修改) ReviseToAop("修改于:2023/7/30&quo…...
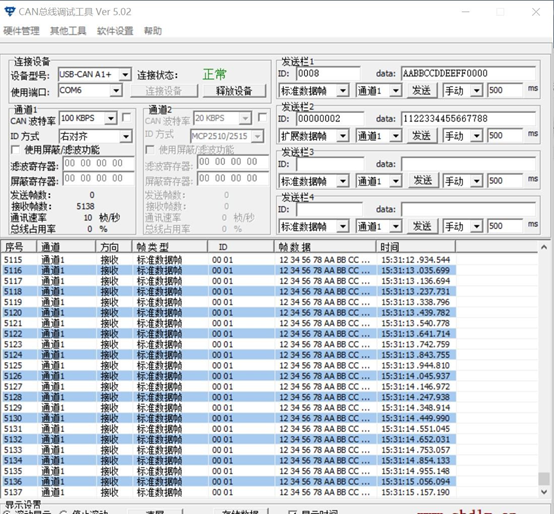
CAN转ETHERCAT网关将CAN 总线和 ETHERCAT 网络连接方法
由于好多现场会出现将CAN总线的设备接到EtherCAT网络中,由于协议的不相同,不能直接进行连接,现需一种能同时兼容CAN 总线和ETHERCAT网络的一种设备,由此捷米JM-ECT-CAN 是自主研发的一款 ETHERCAT 从站功能的通讯网关。该产品主要…...
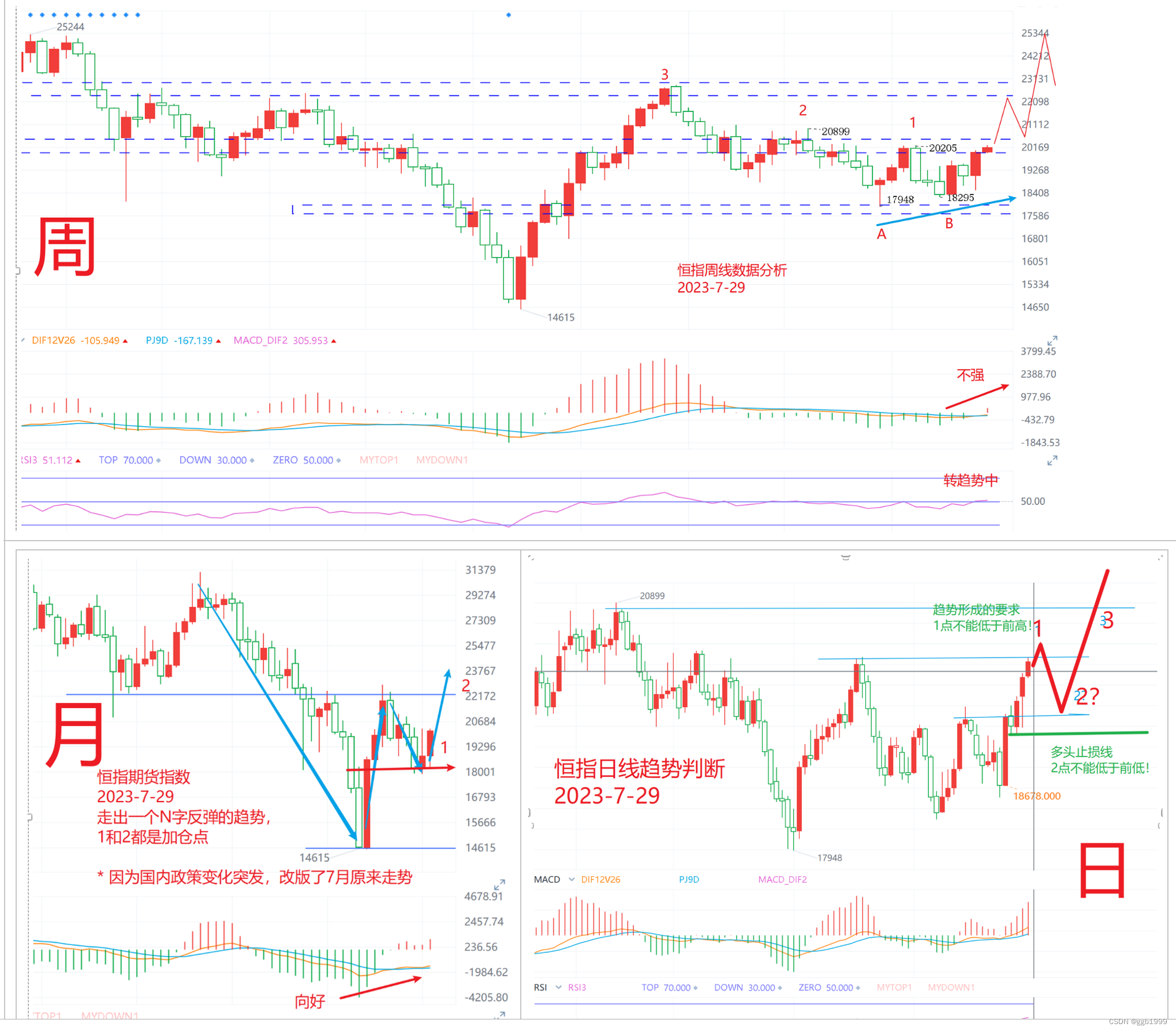
【大数据趋势】7月30日 汇率,恒指期货的大数据趋势概率分析。
1. 数据源头之一 : 汇率变化 从程序模拟趋势来看,美元在持续弱势状态,周线上正在构建一个新的下跌趋势,而且正在反抽过程中,即将完成,如果没有外部干预,会顺势往下。从月线来看,高点逐步降低&a…...
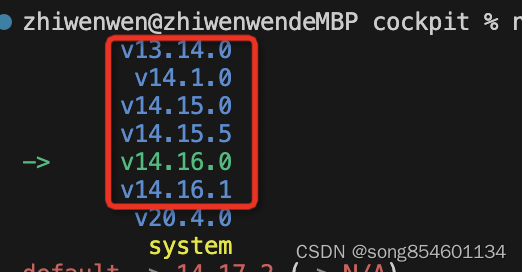
mac使用mvn下载node-sass 会Binary download failed, trying source
m1 上使用nvm 以下node的版本可以直接下载(Binary download,而不是 trying source)而不用切换mac cpu架构 zhiwenwenzhiwenwendeMBP cockpit % nvm install 14.15.5 Downloading and installing node v14.15.5... Downloading https://node…...

【C++】开源:Muduo网络库配置与使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍Muduo网络库配置与使用。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下…...

VCS ICO - Intelligent Coverage Optimization
ico是vcs提供的用于优化覆盖率的feature;一般用户通过dist solver bofore等约束了变量的随机概率,而ico会在用户约束的基础上,做一些自动“修正”,以此来优化随机激励,提高随机多样性,加速覆盖率收敛&#…...
【分布式系统】分布式系统的8个谬误
网络可靠 对于分布式系统来说,网络、计算、存储是三大基石,系统之间进行拆分隔离之后,那么必定存在网络通讯,而网络是最不可靠的。 不管是从硬件层面还是软件层面来说,网络是不可靠的。(断电、配置错误、ID…...
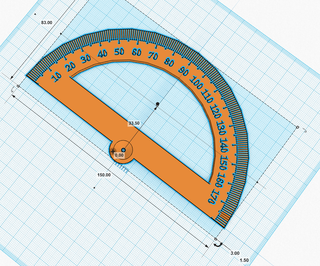
tinkerCAD案例:25. 量角器 - 测量角度
tinkerCAD案例:25. 量角器 - 测量角度 原文 Now we’re going to make a protractor! A Protractor is one of the most basic, but essential, tools for making measurements. It is, then, surprising that the modern protractor is barely over 200 years ol…...

Flutter 使用texture_rgba_renderer实现桌面端渲染视频
Flutter视频渲染系列 第一章 Android使用Texture渲染视频 第二章 Windows使用Texture渲染视频 第三章 Linux使用Texture渲染视频 第四章 全平台FFICustomPainter渲染视频 第五章 Windows使用Native窗口渲染视频 第六章 桌面端使用texture_rgba_renderer渲染视频(本…...

linux虚拟机开机后桌面显示CentOS-7.5-x86盘片文件,并且无法远程连接虚拟机?
在虚拟机启动后遇到了显示CentOS-7.5-x86光盘片文件的问题,并且无法远程连接到虚拟机,有几个可能的解决方法: 检查虚拟机设置:确保虚拟机的网络适配器已正确配置,并且虚拟机配置的网络选项是桥接模式或 NAT 模式&#…...
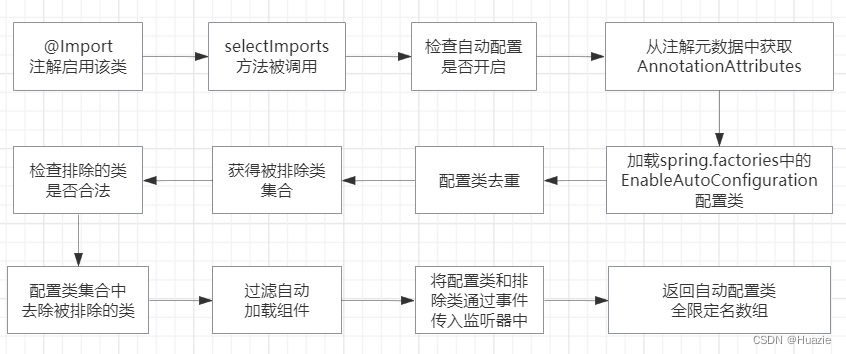
【Spring Boot 源码学习】走近 AutoConfigurationImportSelector
AutoConfigurationImportSelector 源码解析 引言主要内容1. ImportSelector 接口2. DeferredImportSelector 接口3. AutoConfigurationImportSelector 功能概述 总结 引言 上篇博文我们了解了 EnableAutoConfiguration 注解,其中真正实现自动配置功能的核心实现者 …...
)
系统学习Linux-MySQL数据库备份(四)
一、概述 数据库备份是指将数据库中的数据、表格、视图、存储过程、触发器等信息备份到另一个地方,一遍在数据库丢失或损坏时进行恢复,数据库备份是数据库管理中必不可少的一项工作,通过备份可以保护数据库中的数据和业务。 二、数据备份的…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...
