线段树详解 原理解释 + 构建步骤 + 代码(带模板)
目录
介绍:
定义:
以具体一个题目为例:
树的表示方法:
实现步骤:
构建结点属性:
pushup函数:
build函数:
pushdown函数:
modify函数:
query函数:
如何记忆:
模板:
介绍:
线段树(Segment Tree)是一种常用的数据结构,用于解决涉及区间查询的问题。它主要用于在数组或列表等数据结构上支持以下两类查询操作:
- 区间查询:查询某个区间内的统计信息,例如求和、最大值、最小值等。
- 区间更新:修改数组中某个区间元素的值,并相应地更新线段树中的信息。
核心思想是将原始数据递归地划分成一系列不相交的区间,并在每个区间上维护一些预先计算好的信息,以支持高效的区间查询。
定义:
假设我们有一个包含 N 个元素的数组 A,线段树 T 是基于数组 A 的线段树。线段树 T 是一个满二叉树,它具有以下性质:
- 根节点表示整个数组的区间 [1, N]。
- 如果一个节点表示的区间是 [left, right],则它的左子节点表示的区间是 [left, mid],右子节点表示的区间是 [mid+1, right],其中 mid 是 left 和 right 的中间值。
- 叶子节点表示数组 A 中的单个元素,而内部节点表示对应区间上的预计算信息(如区间和、区间最大值等)。
- 线段树通常使用数组来模拟实现。
线段树算法一般包含以下五个函数:
1.build(); 初始构建一个线段树。
2.pushpu(); 向上传递信息。
3.pushdown(); 向下传递懒标记,并且更新子树。
4.modify(); 修改某一区间。
5.query(); 查询某一区间信息。
下面我们一个一个来介绍。
以具体一个题目为例:
下面解析以此题目为例子。
树的表示方法:
我们用 tr 数组来模拟这颗树。
假设根节点在 tr 数组中的的下标为为 i,那么其左右子树的下标为:
左:i * 2 (i << 1)
右:i * 2 + 1 (i << 1 | 1)
我们一般使用位运算,也就是括号里的,含义是一样的。所以可以计算出,tr 数组的长度最多就是题目所给数组长度的4倍。
实现步骤:
事先把输入的数组存在 w数组 中。
构建结点属性:
树结点其实就是一个区间,所以属性包含:左右边界,懒标记。
此题的懒标记就是区间需要加上的值 d 。
根据题目我们还需要查询区间的元素和,所以在其中添加一个 sum。
struct Node
{int l, r;LL sum;LL add; // 懒标记
}tr[N * 4];;pushup函数:
我们在 build 一颗树之前,要先写 pushup 函数,用于向上传递信息,因为我们只知道叶子结点的值,我们要用后序遍历去构建父亲,所以要用到 pushup ,根据题目,我们要向上传递的信息显然是左右子树的 sum 和,这样就可以算出父亲的 sum 。
void pushup(int u) // 向上传递信息
{tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}build函数:
接下来我们开始构建这颗树,若区间内只有一个元素(l == r),说明我们找到了叶子结点,给叶子结点赋值,若不是结子节点(l != r),就继续向左右子树递归,在递归完成时(后序遍历)使用pushup,通过已经获得值的子树去更新父亲。
void build(int u, int l, int r)
{if (l == r) tr[u] = {l, r, w[l], 0}; // 叶子节点else{tr[u] = {l, r};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); // 若不是叶子节点,向下递归pushup(u); // 通过子树构建父亲}
}pushdown函数:
pushdown函数是给子树传递懒标记的,如果懒标记不为空,就将父亲的懒标记传递给左右子树,并且通过懒标记更新左右子树的信息,此题求的是sum,所以子树的 sum 值就要加上区间长度乘上父亲的懒标记,最后清空父亲的懒标记。
注意:懒标记表示的子树需要添加的信息,不包含父亲自己,所以在传递懒标记时,才要传递懒标记同时更新子树。
void pushdown(int u)
{auto &root = tr[u], &left = tr[u << 1], & right = tr[u << 1 | 1];if (root.add){// 传递懒标记并且更新子树left.add += root.add, left.sum += (LL)(left.r - left.l + 1) * root.add;right.add += root.add, right.sum += (LL)(right.r - right.l + 1) * root.add;root.add = 0; // 删除懒标记}
}modify函数:
修改区间信息,如果当前遍历的结点区间已经在区间中,那么就直接给其加上懒标记,并且计算更新其 sum。如果当前遍历的结点区间中的一部分是需要修改的区间,那么就先向下传递懒标记pushdown,然后在向需要修改的左右子树去递归,后序返回时,要给更新父亲pushup。
void modify(int u, int l, int r, int v)
{// 结点在要修改的区间中if (l <= tr[u].l && r >= tr[u].r){tr[u].sum += (tr[u].r - tr[u].l + 1) * v;tr[u].add += v; // 加上懒标记}else{pushdown(u); // 先传递懒标记int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) modify(u << 1, l, r, v);if (r > mid) modify(u << 1 | 1, l, r, v);pushup(u); // 更新父亲}
}query函数:
用于查询区间信息,这里就是查询区间的sum。若遍历到的结点区间在查询区间之中,就返回其sum,若结点区间只有一部分在查询区间中,一样的,也是先传递懒标记,然后继续向需要计算的左右子树去递归,后序返回时计算结果。
LL query(int u, int l, int r)
{if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum; // 返回区间信息pushdown(u); // 也是先传递懒标记LL v = 0;int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) v = query(u << 1, l, r);if (r > mid) v += query(u << 1 | 1, l, r);return v;
}如何记忆:
最重要的是注意每个函数pushup,pushdown函数的位置。只有在modify函数才两个一起用。
build函数只用一个pushup,query函数只用一个pushdown。
模板:
根据具体题目,自行修改。
// 操作是给区间每一个数加d
// 询问是求某一区间和
#include<iostream>using namespace std;typedef long long LL;
const int N = 100010;int w[N];
int n, m;struct Node
{int l, r;LL sum;LL add; // 懒标记
}tr[N * 4];;void pushup(int u) // 向上传递信息
{tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void pushdown(int u)
{auto &root = tr[u], &left = tr[u << 1], & right = tr[u << 1 | 1];if (root.add){// 传递懒标记并且更新子树left.add += root.add, left.sum += (LL)(left.r - left.l + 1) * root.add;right.add += root.add, right.sum += (LL)(right.r - right.l + 1) * root.add;root.add = 0; // 删除懒标记}
}
void build(int u, int l, int r)
{if (l == r) tr[u] = {l, r, w[l], 0}; // 叶子节点else{tr[u] = {l, r};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); // 若不是叶子节点,向下递归pushup(u); // 通过子树构建父亲}
}
void modify(int u, int l, int r, int v)
{// 结点在要修改的区间中if (l <= tr[u].l && r >= tr[u].r){tr[u].sum += (tr[u].r - tr[u].l + 1) * v;tr[u].add += v; // 加上懒标记}else{pushdown(u); // 先传递懒标记int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) modify(u << 1, l, r, v);if (r > mid) modify(u << 1 | 1, l, r, v);pushup(u); // 更新父亲}
}LL query(int u, int l, int r)
{if (l <= tr[u].l && r >= tr[u].r) return tr[u].sum; // 返回区间信息pushdown(u); // 也是先传递懒标记LL v = 0;int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) v = query(u << 1, l, r);if (r > mid) v += query(u << 1 | 1, l, r);return v;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++i) scanf("%d", &w[i]); // 读入数组build(1, 1, n); // 以1为根节点,1~n区间建树char op[2];int l, r, t;// 读入修改和查询,q是查询,否则是修改while (m -- ){scanf("%s%d%d", op, &l, &r);if (*op == 'Q') printf("%lld\n", query(1, l, r));else{scanf("%d", &t);modify(1, l, r, t);}}return 0;
}相关文章:

线段树详解 原理解释 + 构建步骤 + 代码(带模板)
目录 介绍: 定义: 以具体一个题目为例: 树的表示方法: 实现步骤: 构建结点属性: pushup函数: build函数: pushdown函数: modify函数: query…...

Java中Timer的使用
Timer 简述 在Java中,Timer(计时器)是一个用于安排定时任务的类。它可以实现在指定的时间间隔或指定的时间点执行某项任务或操作。 简单的来说Timer就是在Java中用来实现定时任务的工具。 Timer的API Timer中有两API可以使用分别是schedule…...

关于EJB,这两文把热闹和门道都说清楚了
关于技术的很多概念,如果你是小白,不建议看官网。原因就在于官网描述太抽象,就像八股文,看完感觉好像说了很多,但回过头又感觉似乎啥都没说。太虚、不接地气,是最大毛病。其实这些官网的打太极式的表述&…...

MixFormerV2: Efficient Fully Transformer Tracking
摘要 基于变压器的跟踪器在标准基准测试上取得了很强的精度。然而,它们的效率仍然是在GPU和CPU平台上实际部署的一个障碍。在本文中,为了克服这一问题,我们提出了一个完全变压器跟踪框架,称为MixFormerV2,没有任何密集…...
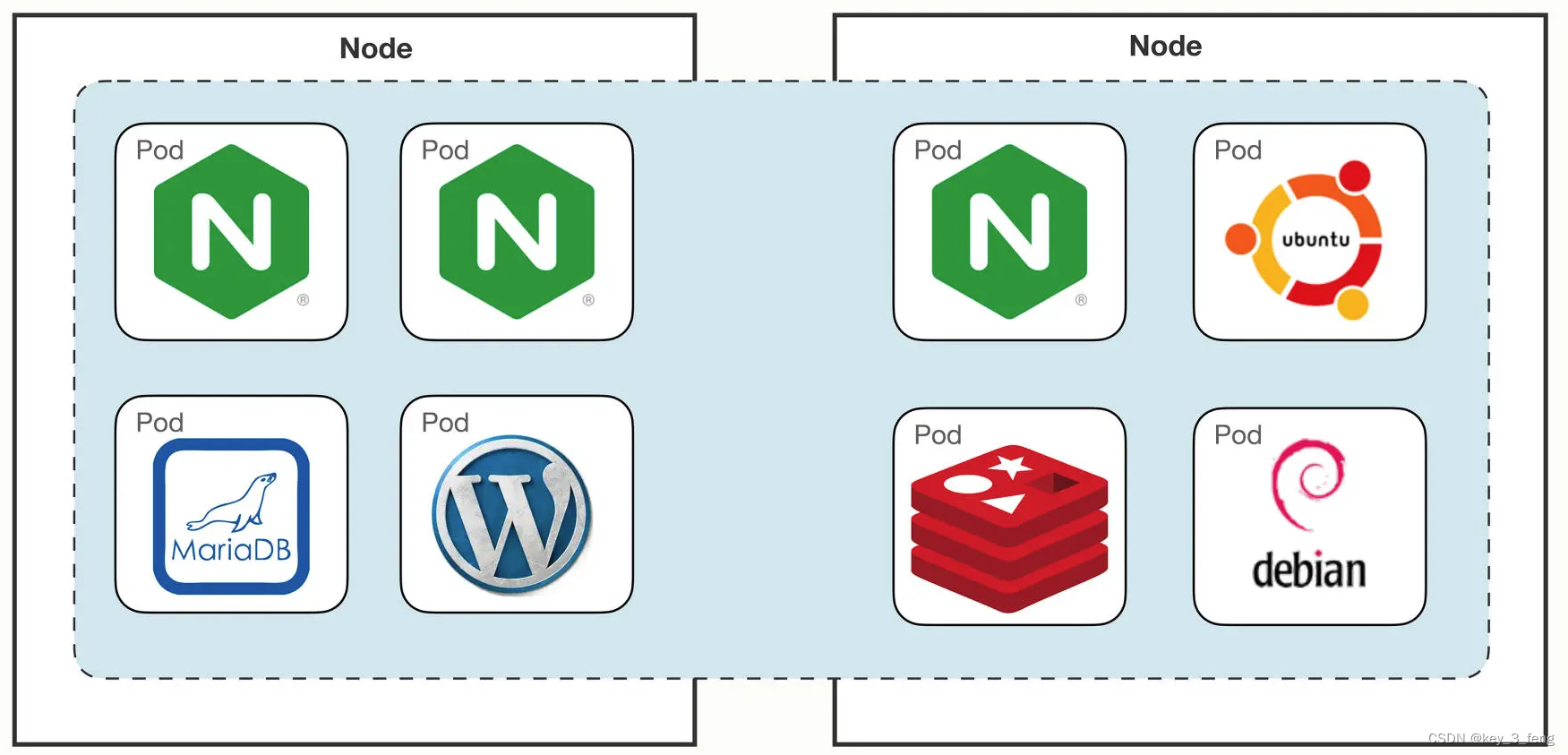
K8S中网络如何通信
Kubernetes 提出了一个自己的网络模型“IP-per-pod”,能够很好地适应集群系统的网络需求,它有下面的这 4 点基本假设: 集群里的每个 Pod 都会有唯一的一个 IP 地址。Pod 里的所有容器共享这个 IP 地址。集群里的所有 Pod 都属于同一个网段。…...
)
LangChain Agents深入剖析及源码解密上(三)
AutoGPT案例V1版本 AutoGPT是一个实验性的开源应用程序,展示了GPT-4语言模型的功能,AutoGPT程序由GPT-4驱动,将大语言模型的思考链接在一起,以自主实现设定的任何目标。作为GPT-4完全自主运行的首批例子之一,AutoGPT突破了人工智能的可能性。LangChain框架复现了https://g…...
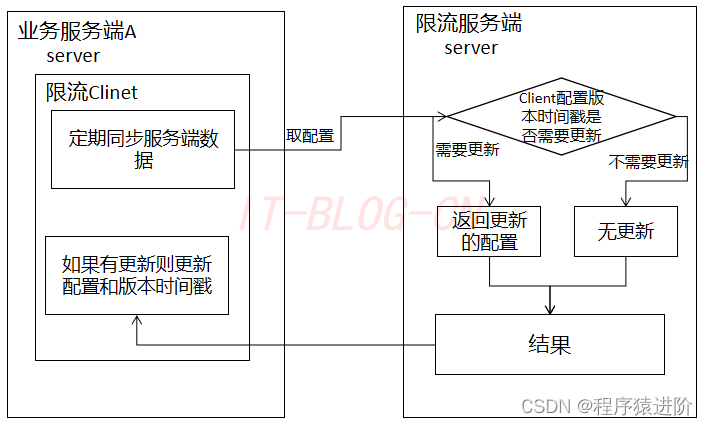
分布式限流方案及实现
优质博文:IT-BLOG-CN 一、限流的作用和意义 限流是对高并发访问进行限制,限速的过程。通过限流来限制资源,可以提高系统的稳定性和可靠性,控制系统的负载,削峰填谷,保证服务质量。 服务限流后的常见处理…...
vuejs源码阅读之优化器
前面讲过vuejs中解析器是把html模版解析成AST,而优化器的作用是在AST中找到静态子树并打上标记。 静态子树是指的那些在AST中永远不会发生变化的节点。 例如,一个纯文本节点就是静态子树,而带变量的文本节点就不是静态子树,因为…...

【C++】-动态内存管理
作者:小树苗渴望变成参天大树 作者宣言:认真写好每一篇博客 作者gitee:gitee 如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点 点 关 注 吧! 文章目录 前言一、C内存管理方式1.1 new/delete操作内置类型 总结 前言 今天再讲一个…...

微服务SpringCloud教程——微服务是什么
微服务(MicroServices)最初是由 Martin Fowler 于 2014 年发表的论文《MicroServices》中提出的名词,它一经提出就成为了技术圈的热门话题。 微服务,我们可以从字面上去理解,即“微小的服务”,下面我们从“…...
RNN架构解析——LSTM模型
目录 LSTMLSTM内部结构图 Bi-LSTM实现 优点和缺点 LSTM LSTM内部结构图 Bi-LSTM 实现 优点和缺点...

苹果电脑系统优化工具:Ventura Cache Cleaner for mac
Ventura Cache Cleaner for Mac是一款专门为苹果电脑开发的系统优化工具,旨在帮助用户清理和优化Mac电脑,提高系统性能和速度。该软件由美国公司Northern Softworks开发,已经推出了多个版本,适用于不同版本的Mac操作系统。 Ventu…...

为了爱人穿越沙漠-心理测试
我觉得很准的一个心理测试。我的答案反射出我的态度,它们是100%的贴切。有兴趣的朋友也不妨一试。 你有一个深爱着的心上人,然而你们却被一片无垠的沙漠相隔两地,你禁不住思念的折磨,决定穿越沙漠去寻找你心中的那个爱人…… 1、…...
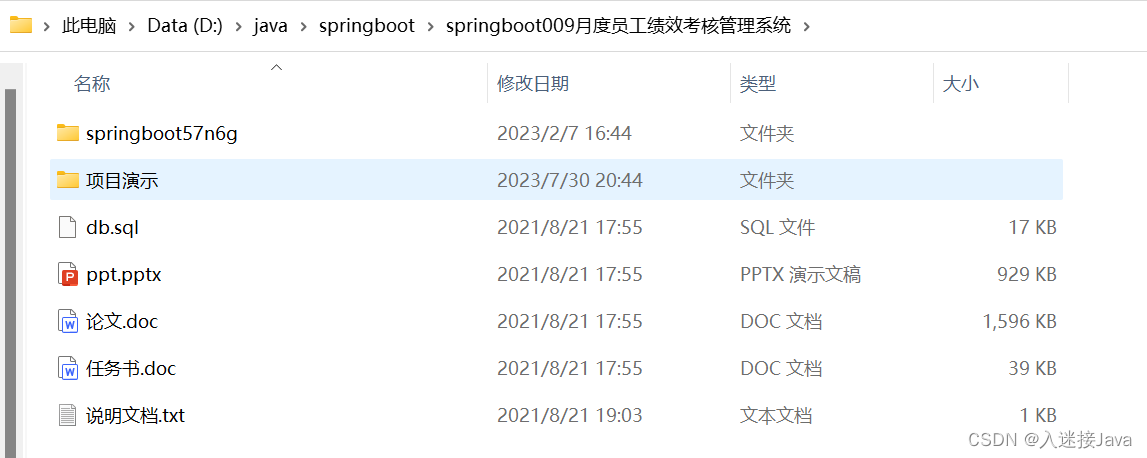
SpringBoot月度员工绩效考核管理系统【附任务书|ppt|万字文档(LW)和搭建文档】
主要功能 员工登录: ①首页、个人中心:修改密码、个人信息管理等 ②公告信息管理、绩效指标管理、绩效考核管理 管理员登录: ①首页、个人中心:修改密码、个人信息管理等 ②公告信息管理、部门管理、岗位管理、员工管理、绩效指标…...

【新星计划】STM32F103C8T6 - C语言 - 蓝牙JDY-31-SPP串口通信实验
文章目录 蓝牙技术的发展历史SPP蓝牙串口BLE协议(超低功耗应用蓝牙协议) 常见通用蓝牙模块JDY-31-SPPHC05/06 Keil 工程开发模版main.c 源文件:接线方式:烧录工具:FlyMcu串口调试工具:XCOM蓝牙调试助手APP …...
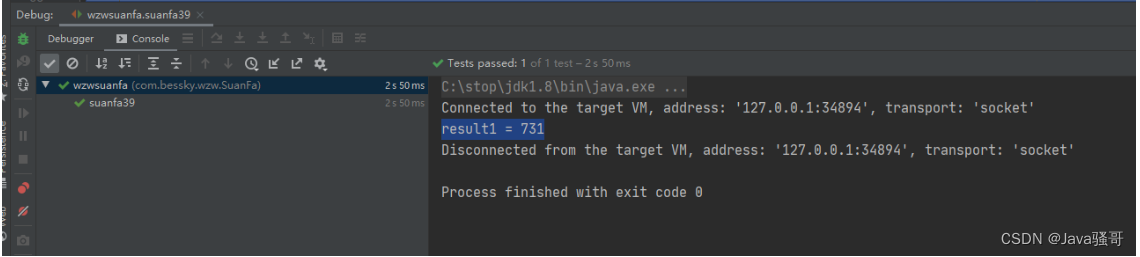
算法39:Excel 表列序号
一、需求 给你一个字符串 columnTitle ,表示 Excel 表格中的列名称。返回 该列名称对应的列序号 。 例如: A -> 1 B -> 2 C -> 3 … Z -> 26 AA -> 27 AB -> 28 … 示例 1: 输入: columnTitle “A” 输出: 1 示例 2&…...

Android:ImageView xml方式配置selector 图片切换
1、在res/drawable目录下创建一个新的XML文件,比如selector_image.xml <?xml version"1.0" encoding"utf-8"?> <selector xmlns:android"http://schemas.android.com/apk/res/android"> <!-- 背景选择器 state_pre…...
Spring Boot 缓存 Cache 入门
Spring Boot 缓存 Cache 入门 1.概述 在系统访问量越来越大之后,往往最先出现瓶颈的往往是数据库。而为了减少数据库的压力,我们可以选择让产品砍掉消耗数据库性能的需求。 当然也可以引入缓存,在引入缓存之后,我们的读操作的代码ÿ…...
如何关闭谷歌浏览器自动更新
适用范围: 写自动化脚本时,需要安装浏览器驱动,安装浏览器驱动时需要下载对应的浏览器驱动版本,如果浏览器版本一直在自动更新的话,自动化脚本会报错浏览器版本和浏览器驱动不匹配,所以建议关闭谷歌浏览器自动更新&am…...
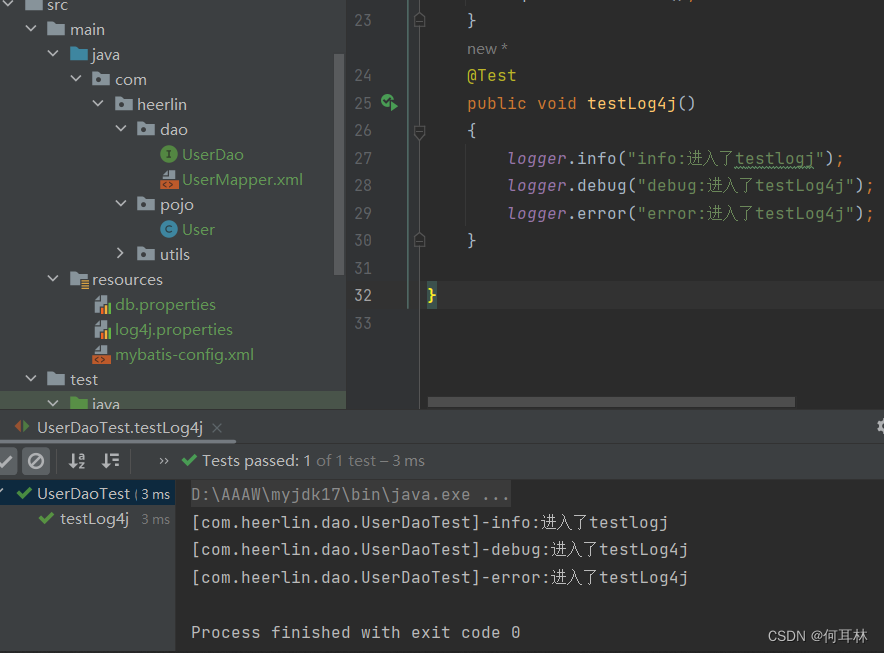
mybatis日志工厂
前言: 如果一个数据库操作,出现异常,我们需要排错,日志就是最好的助手 官方给我们提供了logImpl:指定 MyBatis 所用日志的具体实现,未指定时将自动查找。 默认工厂: 在配置文件里添加…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
