LA@复数和复矩阵@实对称阵相关定理
文章目录
- 复数🎈
- 复矩阵和复向量
- 共轭矩阵
- 性质
- 定理@实对称阵的相关定理
复数🎈
-
复数 (数学) (wikipedia.org)
-
加法:(a+bi)+(c+di)=(a+c)+(b+d)i)减法:(a+bi)−(c+di)=(a−c)+(b−d)i)乘法:(a+bi)(c+di)=ac+bci+adi+bdi2=(ac−bd)+(bc+ad)i除法:(a+bi)(c+di)=(a+bi)(c−di)(c+di)(c−di)=ac+bci−adi−bdi2c2−(di)2=(ac+bd)+(bc−ad)ic2+d2=(ac+bdc2+d2)+(bc−adc2+d2)i加法:(a+bi)+(c+di)=(a+c)+(b+d)i)\\ 减法:(a+bi)-(c+di)=(a-c)+(b-d)i)\\ 乘法:(a+bi)(c+di)=ac+bci+adi+bdi^{2}=(ac-bd)+(bc+ad)i\\ 除法:{\frac {(a+bi)}{(c+di)}} ={\frac {(a+bi)(c-di)}{(c+di)(c-di)}} ={\frac {ac+bci-adi-bdi^{2}}{c^{2}-(di)^{2}}}\\ ={\frac {(ac+bd)+(bc-ad)i}{c^{2}+d^{2}}} =\left({ac+bd \over c^{2}+d^{2}}\right)+\left({bc-ad \over c^{2}+d^{2}}\right)i 加法:(a+bi)+(c+di)=(a+c)+(b+d)i)减法:(a+bi)−(c+di)=(a−c)+(b−d)i)乘法:(a+bi)(c+di)=ac+bci+adi+bdi2=(ac−bd)+(bc+ad)i除法:(c+di)(a+bi)=(c+di)(c−di)(a+bi)(c−di)=c2−(di)2ac+bci−adi−bdi2=c2+d2(ac+bd)+(bc−ad)i=(c2+d2ac+bd)+(c2+d2bc−ad)i
-
z=a+ib的共轭复数定义为z=a−ib;记作z‾或z∗z=a+ib的共轭复数定义为 z=a-ib;记作 \overline {z}或z^{*}z=a+ib的共轭复数定义为z=a−ib;记作z或z∗
- zzˉ=(a+bi)(a−bi)=a2−b2i2=a2+b2z\bar{z}=(a+bi)(a-bi)=a^2-b^2i^2=a^2+b^2zzˉ=(a+bi)(a−bi)=a2−b2i2=a2+b2
- −z=−a−ib-z=-a-ib−z=−a−ib
- z‾=a−ib\overline{z}=a-ibz=a−ib
- −z‾=−a+ib\overline{-z}=-a+ib−z=−a+ib
- −z‾=−z‾\overline{-z}=-\overline{z}−z=−z
z‾是z关于实数轴的对称点。有z+w‾=z‾+w‾zw‾=z‾⋅w‾(zw)‾=z‾w‾z‾‾=zz‾=z当且仅当z是实数∣z∣=∣z‾∣∣z∣2=zz‾z−1=z‾∣z∣−2若z非零。这是计算乘法逆最常用的等式。\overline {z}是z关于实数轴的对称点。有\\ \overline {z+w}=\overline {z}+\overline {w}\\ \overline {zw}=\overline {z}\cdot \overline {w}\\ \overline {\left({\frac {z}{w}}\right)}={\frac {\overline {z}}{\overline {w}}}\\ \overline {\overline {z}}=z\\ \\ \overline {z}=z 当且仅当z是实数\\ |z|=|\overline {z}|\\ |z|^{2}=z\overline {z}\\ z^{{-1}}=\overline {z}|z|^{{-2}}若z非零。这是计算乘法逆最常用的等式。 z是z关于实数轴的对称点。有z+w=z+wzw=z⋅w(wz)=wzz=zz=z当且仅当z是实数∣z∣=∣z∣∣z∣2=zzz−1=z∣z∣−2若z非零。这是计算乘法逆最常用的等式。
- x+y‾=x‾+y‾\overline{x+y}=\overline{x}+\overline{y}x+y=x+y
- x+y=(x1+y1i)+(x2+y2i)=(x1+x2)+(y1+y2)ix+y=(x_1+y_1i)+(x_2+y_2i)=(x_1+x_2)+(y_1+y_2)ix+y=(x1+y1i)+(x2+y2i)=(x1+x2)+(y1+y2)i
- x‾+y‾=x1−y1i+x2−y2i=(x1+x2)−(y1+y2)i\overline{x}+\overline{y}=x_1-y_1i+x_2-y_2i=(x_1+x_2)-(y_1+y_2)ix+y=x1−y1i+x2−y2i=(x1+x2)−(y1+y2)i
- x+y‾=(x1+x2)−(y1+y2)i\overline{x+y}=(x_1+x_2)-(y_1+y_2)ix+y=(x1+x2)−(y1+y2)i
- xy‾=xˉyˉ\overline{xy}=\bar{x}\bar{y}xy=xˉyˉ
- −x‾=−x‾\overline{-x}=-\overline{x}−x=−x
复矩阵和复向量
- 元素是复数的矩阵和向量分别称为复矩阵和复向量
共轭矩阵
- 设aija_{ij}aij是复数,A=(aij)m×n,A‾=(aij‾)m×nA=(a_{ij})_{m\times{n}},\overline{A}=(\overline{a_{ij}})_{m\times{n}}A=(aij)m×n,A=(aij)m×n,aij‾\overline{a_{ij}}aij和aija_{ij}aij互为共轭复数,则称A,A‾A,\overline{A}A,A互为共轭矩阵
性质
-
A‾‾=A\overline{\overline{A}}=AA=A
-
AT‾=A‾T\overline{A^T}=\overline{A}^TAT=AT
-
如果A是实矩阵,则A‾=A\overline{A}=AA=A
-
如果A是实对称阵,则AT‾=A\overline{A^T}=AAT=A
- 对称阵:AT=AA^T=AAT=A
- AT‾=A‾=A\overline{A^T}=\overline{A}=AAT=A=A
-
kA‾=kˉA‾\overline{kA}=\bar{k}\overline{A}kA=kˉA
- k∈Ck\in\mathbb{C}k∈C
-
对于复数x,y,x,y,x,y,有xˉyˉ=xy‾\bar{x}\bar{y}=\overline{xy}xˉyˉ=xy
- 特别的,a∈R,aˉ=aa\in\mathbb{R},\bar{a}=aa∈R,aˉ=a
- a⋅x‾=ax‾a\cdot\overline{x}=\overline{ax}a⋅x=ax
- −x‾=−x‾-\overline{x}=\overline{-x}−x=−x
- +x‾=+x‾+\overline{x}=\overline{+x}+x=+x
- a⋅x‾=ax‾a\cdot\overline{x}=\overline{ax}a⋅x=ax
- 特别的,a∈R,aˉ=aa\in\mathbb{R},\bar{a}=aa∈R,aˉ=a
-
A+B‾=A‾+B‾\overline{A+B}=\overline A+\overline BA+B=A+B
-
AB‾=AˉBˉ\overline{AB}=\bar{A}\bar{B}AB=AˉBˉ
- cij=∑ilaikbkjc_{ij}=\sum_{i}^{l}a_{ik}b_{kj}cij=∑ilaikbkj
- cijˉ=∑inaikbkj‾\bar{c_{ij}}=\sum_{i}^{n}\overline{a_{ik}b_{kj}}cijˉ=∑inaikbkj
- =∑inaˉikbkjˉ=\sum_i^n{\bar a_{ik}\bar{b_{kj}}}=∑inaˉikbkjˉ
-
(AB)T‾=BTAT‾=BT‾AT‾\overline{(AB)^T}=\overline{B^TA^T}=\overline{B^T}\ \overline{A^T}(AB)T=BTAT=BT AT
-
注意公式的逆用
- A‾+B‾=A+B‾\overline A+\overline B=\overline{A+B}A+B=A+B
- AˉBˉ=AB‾\bar{A}\bar{B}=\overline{AB}AˉBˉ=AB
-
公式推广
- ∑ai‾=∑ai‾∏iai‾=∏iai‾∑i∏jai,ji‾=∑i∏jai,ji‾∑iki∏jai,ji‾=∑iki∏jai,ji‾\sum{\overline{a_i}}=\overline{\sum{a_i}} \\ \prod_{i}\overline{a_i}=\overline{\prod_{i}a_i} \\ \sum_{i}{\prod_{j}\overline{a_{i,j_i}}}= \overline{\sum_{i}{\prod_{j}a_{i,j_i}}} \\ \sum_{i}k_i{\prod_{j}\overline{a_{i,j_i}}}= \overline{\sum_{i}k_i{\prod_{j}a_{i,j_i}}} ∑ai=∑aii∏ai=i∏aii∑j∏ai,ji=i∑j∏ai,jii∑kij∏ai,ji=i∑kij∏ai,ji
-
若A可逆,则A−1‾=(A‾)−1\overline{A^{-1}}=(\overline{A})^{-1}A−1=(A)−1
- A‾(A‾)−1=EA‾(A−1‾)=AA−1‾=E‾=E\overline{A}(\overline{A})^{-1}=E \\ \overline{A}(\overline{A^{-1}})=\overline{AA^{-1}}=\overline{E}=E A(A)−1=EA(A−1)=AA−1=E=E
-
∣A‾∣=∣A∣‾\large |\overline{A}|=\overline{|A|}∣A∣=∣A∣
- ∣A‾∣=∑k(−1)τ(pk)∏i=1nθi‾=∑k(−1)τ(pk)∏i=1nθi‾=∣A∣‾|\overline{A}|= \sum\limits_{k}{(-1)}^{\tau(p_k)}\prod_{i=1}^{n}{\overline{\theta_{i}}} =\overline{\sum\limits_{k}{(-1)}^{\tau(p_k)}\prod_{i=1}^{n}{\theta_{i}}} =\overline{|A|} ∣A∣=k∑(−1)τ(pk)i=1∏nθi=k∑(−1)τ(pk)i=1∏nθi=∣A∣
定理@实对称阵的相关定理
-
实对称阵的特征值都是实数
-
设λ\lambdaλ是实对称阵A的任意一个特征值
- Aα=λα,α≠0A\alpha=\lambda\alpha,\alpha\neq{0}Aα=λα,α=0
- αˉ≠0\bar\alpha\neq{0}αˉ=0
- (αˉ)Tα>0(\bar\alpha)^T\alpha>0(αˉ)Tα>0
- (αˉ)Tα=∑in(ai2+bi2)(\bar\alpha)^T\alpha=\sum_{i}^{n}(a_i^2+b_i^2)(αˉ)Tα=∑in(ai2+bi2)
- A‾=A,AT=A\overline{A}=A,A^T=AA=A,AT=A
- (A‾)T=AT‾(\overline{A})^T=\overline{A^T}(A)T=AT
- Aα=λα,α≠0A\alpha=\lambda\alpha,\alpha\neq{0}Aα=λα,α=0
-
需要证明的内容是λˉ=λ\bar\lambda=\lambdaλˉ=λ
-
(αˉ)T(Aα)=(αˉ)TATα=(Aαˉ)Tα=(Aˉαˉ)Tα=(Aα‾)Tα两端分别用Aα=λα代入(αˉ)Tλα=(λα‾)Tαλ(αˉ)Tα=(λ‾αˉ)Tα=λ‾(αˉ)Tα(λ−λˉ)(αˉ)Tα=0(\bar\alpha)^T(A\alpha)=(\bar\alpha)^TA^T\alpha =(A\bar\alpha )^T\alpha=(\bar{A}\bar\alpha)^T\alpha =(\overline{A\alpha})^T\alpha \\两端分别用A\alpha=\lambda{\alpha}代入 \\ (\bar{\alpha})^T\lambda\alpha=(\overline{\lambda\alpha})^T\alpha \\ \lambda(\bar\alpha)^T\alpha=(\overline{\lambda}\bar\alpha)^T\alpha =\overline{\lambda}(\bar\alpha)^T\alpha \\ (\lambda-\bar\lambda)(\bar\alpha)^T\alpha=0 \\ (αˉ)T(Aα)=(αˉ)TATα=(Aαˉ)Tα=(Aˉαˉ)Tα=(Aα)Tα两端分别用Aα=λα代入(αˉ)Tλα=(λα)Tαλ(αˉ)Tα=(λαˉ)Tα=λ(αˉ)Tα(λ−λˉ)(αˉ)Tα=0
- 这里左乘的是(αˉ)T(\bar{\alpha})^T(αˉ)T而不是αˉ\bar{\alpha}αˉ是为了使得乘法可以执行(规格)
- (αˉ)Tα>0(\bar\alpha)^T\alpha>0(αˉ)Tα>0,所以λ−λˉ=0\lambda-\bar{\lambda}=0λ−λˉ=0,即λ=λˉ\lambda=\bar\lambdaλ=λˉ
-
-
实对称阵的关于不同特征值的特征向量彼此正交
-
设λ,μ\lambda,\muλ,μ是实对称阵的两个不同的特征值(λ≠μ\lambda\neq{\mu}λ=μ),Aα=λα;Aβ=μβA\alpha=\lambda\alpha;A\beta=\mu\betaAα=λα;Aβ=μβ
-
λ(α,β)=(λα,β)=(Aα,β)=(Aα)Tβ=αTATβ=αTAβ=αT(Aβ)=(α,Aβ)=(α,μβ)=μ(α,β)(λ−μ)(α,β)=0∵λ≠μ∴(α,β)=0\lambda(\alpha,\beta)=(\lambda\alpha,\beta)=(A\alpha,\beta) \\=(A\alpha)^T\beta=\alpha^TA^T\beta =\alpha^TA\beta=\alpha^T(A\beta) \\=(\alpha,A\beta)=(\alpha,\mu\beta)=\mu(\alpha,\beta) \\ (\lambda-\mu)(\alpha,\beta)=0 \\ \because{\lambda}\neq{\mu} \\ \therefore (\alpha,\beta)=0 λ(α,β)=(λα,β)=(Aα,β)=(Aα)Tβ=αTATβ=αTAβ=αT(Aβ)=(α,Aβ)=(α,μβ)=μ(α,β)(λ−μ)(α,β)=0∵λ=μ∴(α,β)=0
-
Aαi=λiαiA\alpha_i=\lambda_i\alpha_iAαi=λiαi,i=1,⋯,si=1,\cdots,si=1,⋯,s,(αi,αj)=0,(λi≠λj)(\alpha_i,\alpha_j)=0,(\lambda_i\neq{\lambda_j})(αi,αj)=0,(λi=λj)
- s表示A有s个互异的特征值
-
-
实对称阵的可对角化条件和一般方阵可对角化的条件相仿
-
n阶实对称阵一定有n个正交的单位特征向量Φ=α1,⋯,αn\Phi=\alpha_1,\cdots,\alpha_nΦ=α1,⋯,αn
- 因为可以将可对角化实对称阵的n个线性无关向量进行
- Gram-Schmidt orthogonalization方法正交化
- 再进行单位化
- 记Q=(Φ)Q=(\Phi)Q=(Φ),则:Q−1AQ=Λ=diag(λ1,⋯,λn)Q^{-1}AQ=\Lambda=diag(\lambda_1,\cdots,\lambda_n)Q−1AQ=Λ=diag(λ1,⋯,λn)
- 因为可以将可对角化实对称阵的n个线性无关向量进行
-
一定存在正交矩阵Q使得实对称阵A满足Q−1AQ=ΛQ^{-1}AQ=\LambdaQ−1AQ=Λ(Λ\LambdaΛ为某个对角阵)
- 换句话说,实对称阵一定可以正交相似对角化
-
如果实矩阵A和某个对角阵Q正交相似(Q−1AQ=ΛQ^{-1}AQ=\LambdaQ−1AQ=Λ),则A一定是对称阵
- (QTQ=EQ^TQ=EQTQ=E)
- 当AAA正交相似于对角阵Λ\LambdaΛ时,即QTAQ=ΛQ^TAQ=\LambdaQTAQ=Λ
- A=(QT)−1ΛQ−1=(Q−1)TΛQ−1A=(Q^T)^{-1}\Lambda{Q^{-1}}=(Q^{-1})^T\Lambda{Q^{-1}}A=(QT)−1ΛQ−1=(Q−1)TΛQ−1
- 而ΛT=Λ\Lambda^T=\LambdaΛT=Λ则:
- AT=(Q−1)TΛTQ−1=(Q−1)TΛQ−1A^T=(Q^{-1})^T\Lambda^TQ^{-1}=(Q^{-1})^T\Lambda Q^{-1}AT=(Q−1)TΛTQ−1=(Q−1)TΛQ−1
- 可见A=AT=(Q−1)TΛQ−1A=A^T=(Q^{-1})^T\Lambda Q^{-1}A=AT=(Q−1)TΛQ−1,说明A是一个对称阵
-
方阵A正交相似于对角阵Λ\LambdaΛ当且仅当AT=AA^T=AAT=A
- 换句话说,方阵A正交相似对角化当且仅当A是个对称阵
相关文章:

LA@复数和复矩阵@实对称阵相关定理
文章目录复数🎈复矩阵和复向量共轭矩阵性质定理实对称阵的相关定理复数🎈 复数 (数学) (wikipedia.org) 加法:(abi)(cdi)(ac)(bd)i)减法:(abi)−(cdi)(a−c)(b−d)i)乘法:(abi)(cdi)acbciadibdi2(ac−bd)(bcad)i除法&…...

cmd set命令笔记
使用 set是cmd最基础的命令,每个人都会用,但其实它还是有些知识的。 set 用来接收入参 set /p var请选择(1或2或3): echo %var%可以接收输入的参数。 set /p var请选择(1或2或3): echo %var% 语法 he…...
IB学校获得IBO授权究竟有多难?
IB 学校认证之路,道阻且长 The road to IB school accreditation is long and difficult一所学校能获得IB授权必须经过IBO非常严格的审核,在办学使命&教育理念、组织架构、师资力量&授课技能、学校硬件设施和课程体系上完全符合标准才可获得授权…...
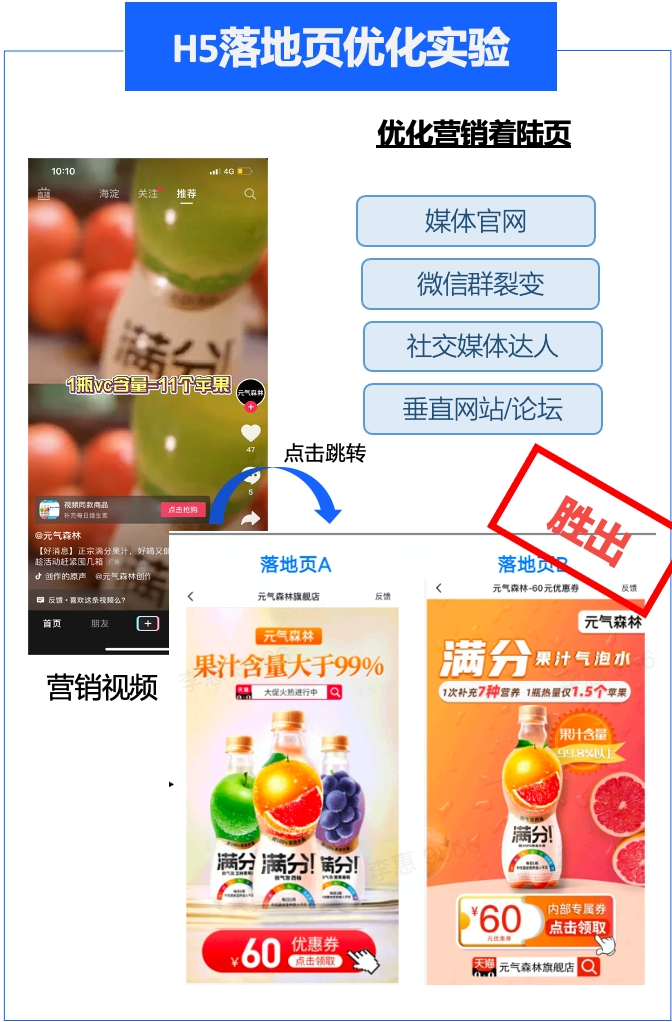
火山引擎 DataTester:A/B 测试,让企业摆脱广告投放“乱烧钱”
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 在广告投放的场景下,一线广告优化师通常会创建多个计划,去测试不同的广告素材效果。这套方法看似科学,实际上却存在诸多问题&…...
黑马redis学习记录:缓存
一、介绍 什么是缓存? 缓存(Cache),就是数据交换的缓冲区,俗称的缓存就是缓冲区内的数据,一般从数据库中获取,存储于本地代码 缓存无处不在 为什么要使用缓存? 因为速度快,好用缓存数据存储于代码中,而…...
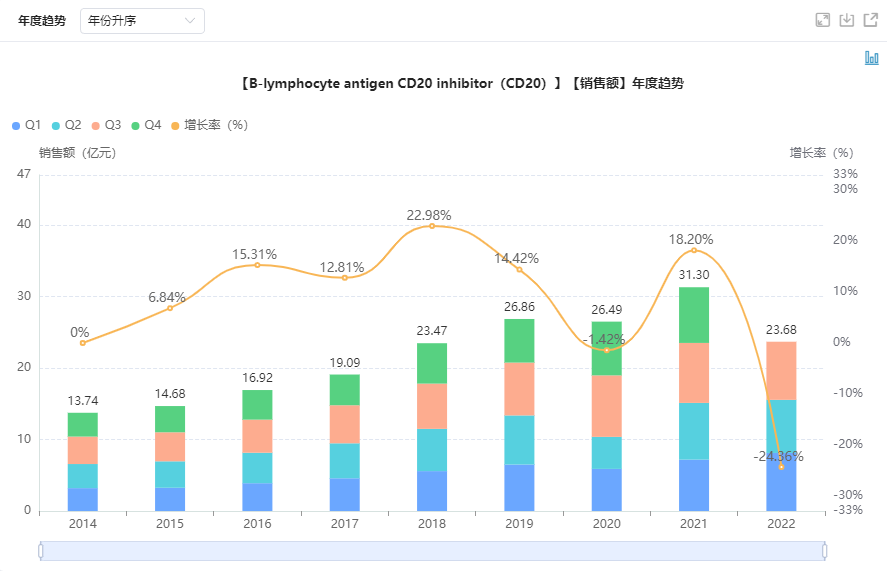
CD20靶向药物|适应症|市场销售-上市药品前景分析
CD20是靶向治疗的第一个靶点,是B细胞淋巴瘤的现代治疗药物。CD20作为治疗剂的使用被认为是方便的,原因有二。首先,在 CD20 阳性肿瘤的情况下,这种受体大量存在于 B 淋巴细胞表面——每个细胞大约有十万个分子。其次,干…...

多源 复制
使复制从属服务器能够同时从多个主服务器接收事务至少需要两个主服务器和一个从属服务器设备从属服务器为每个主服务器创建一个 复制通道从属服务器必须使用基于表的资料档案库多源复制与基于文件的资料档案库不兼容不尝试检测或解决冲突如果需要此功能,则由应用程序…...
微服务项目【消息推送(RabbitMQ)】
创建消费者 第1步:基于Spring Initialzr方式创建zmall-rabbitmq消费者模块 第2步:在公共模块中添加rabbitmq相关依赖 <!--rabbitmq--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-bo…...

vr电力刀闸事故应急演练实训系统开发
电力事故是在电力生产和输电过程中可能发生的意外事件,它们可能会对人们的生命财产安全造成严重的威胁。因此,电力事故应急演练显得尤为重要。而VR技术则可以为电力事故应急演练提供一种全新的解决方案。 在虚拟环境中,元宇宙VR会模拟各种触电…...
C++类和对象补充
目录 前言: 1. 构造函数->初始化列表 1.1 初始化列表出现原因 1.2 初始化列表写法 2. explicit关键字 2.1 explict的出现 2.2 explict的写法 3. static成员 4. 友元 4.1 友元函数 4.2 友元类 5. 内部类和匿名对象 5.1 内部类 5.2 匿名对象 前言&a…...
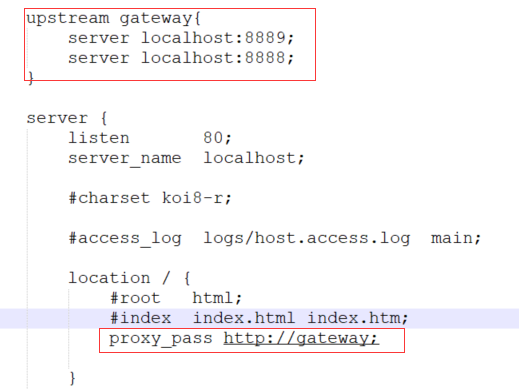
08 SpringCloud 微服务网关Gateway组件
网关简介 大家都都知道在微服务架构中,一个系统会被拆分为很多个微服务。那么作为客户端要如何去调用这么多的微服务呢? 如果没有网关的存在,我们只能在客户端记录每个微服务的地址,然后分别去用。 这样的架构,会存…...
极验3代 加密分析
目标链接 aHR0cHM6Ly93d3cuZ2VldGVzdC5jb20vZGVtby9zbGlkZS1mbG9hdC5odG1s接口分析 极验参数重要信息 gt和challenge;gt是固定的,但是challenge每次请求会产生不同的,这里的请求的并没有什么加密参数。 下一个请求 gettype.php,…...

python 数据分析可视化实战 超全 附完整代码数据
代码数据:https://download.csdn.net/download/qq_38735017/873799141.1 数据预处理1.1.1 异常值检测①将支付时间转为标准时间的过程中发生错误,经排查错误数据为‘2017/2/29’,后将其修改为‘2017/2/27’。②经检测发现部分订单应付金额与实付金额都为…...
有趣的HTML实例(十三) 咖啡选择(css+js)
一个人追求目标的路途是孤单的,一个人独品辛酸的时候是寂寥的,一个人马不停蹄的追赶着,狂奔着,相信前方是一片光明,我从不放弃希望,就像我对生活的信念,没有人可以动摇。 ——《北京青年》 目录…...

【力扣-LeetCode】1139. 最大的以 1 为边界的正方形 C++题解
1139. 最大的以 1 为边界的正方形难度中等137收藏分享切换为英文接收动态反馈给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。示例 1…...
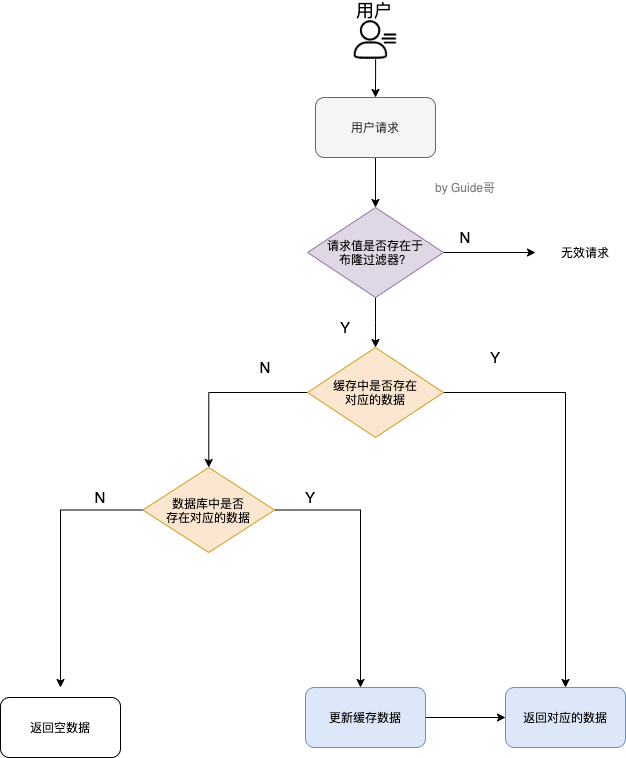
【JavaGuide面试总结】Redis篇·下
【JavaGuide面试总结】Redis篇下1.如何使用 Redis 事务?2.如何解决 Redis 事务的缺陷?3.说说Redis bigkey吧4.大量 key 集中过期问题怎么解决的5.如何保证缓存和数据库数据的一致性?6.缓存穿透有哪些解决办法?7.缓存击穿有哪些解决…...
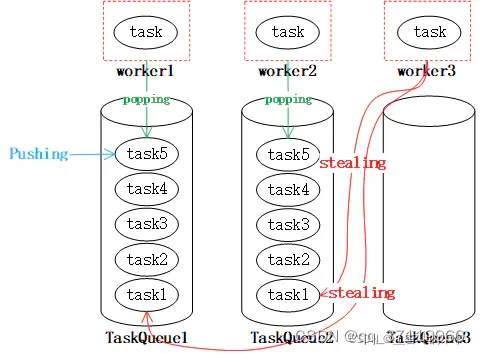
ForkJoinPool原理
1、概述 Fork/Join框架是Java7提供了的一个用于并行执行任务的框架。ForkJoinPool是Java中提供了一个线程池,特点是用来执行分治任务。主题思想是将大任务分解为小任务,然后继续将小任务分解,直至能够直接解决为止,然后再依次将任…...

02 python基本语法和数据类型
基本语法 python脚本可以在python交互式shell或者代码编辑器中编写与运行。python文件的扩展名一般为.py python使用缩进来区分不同的代码块,此特性有利于提高代码可读性。 下面是一个简单的python条件语句代码: 小明=矮穷错 小红=白富美 小华=高富帅 小李=程序员某人 = &quo…...
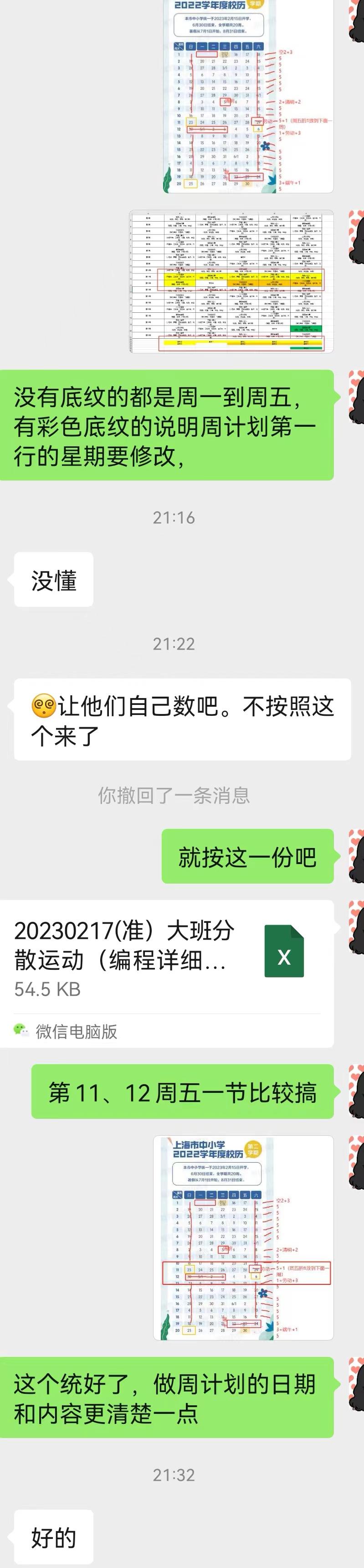
【办公类-16-09】“2022下学期 大班运动场地分配表-跳过节日循环排序”(python 排班表系列)
样例展示:跳过节日的运动场地循环排序表(8个班级8组内容 下学期一共20周)背景需求:上学期做过一次大班运动场地安排,跳过节日。2023.2下学期运动场地排班(跳过节日)又来了。一、场地器械微调二、…...
全网多种方法分析解决HTTP Status 404资源未找到的错误,TCP的3次握手,dns域名解析,发起http请求以及cookie和session的区别
文章目录1. 文章引言2. 简述URL3. http完整请求3.1 DNS域名解析3.2 TCP的3次握手3.3 发起http请求3.4 浏览器解析html代码3.5 浏览器对页面进行渲染呈现给用户4. 解决404错误的方法5. 补充知识点5.1 cookie和session的区别5.2 ChatGPT的介绍1. 文章引言 正赶上最近ChatGPT很火…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
