【算法设计与分析】STL容器、递归算法、分治法、蛮力法、回溯法、分支限界法、贪心法、动态规划;各类算法代码汇总
文章目录
- 前言
- 一、STL容器
- 二、递归算法
- 三、分治法
- 四、蛮力法
- 五、回溯法
- 六、分支限界法
- 七、贪心法
- 八、动态规划
前言
本篇共为8类算法(STL容器、递归算法、分治法、蛮力法、回溯法、分支限界法、贪心法、动态规划),则各取每类算法中的几例经典示例进行展示。
一、STL容器
-
- 使用STL算法sort() 实现整型数组a的递增排序
#include<iostream>
#include <algorithm>
using namespace std;
int main()
{ int a[]={2,5,4,1,3};sort(a,a+5);for (int i=0;i<5;i++)printf("%d ",a[i]); //输出: 1 2 3 4 5printf("\n");
}
-
- 编写一个实验程序,对于一个含n(n>1)个元素的queue队列容器qu,出队从队头到队尾的第k(1<=k<=n)个元素,其他队列元素不变。
#include<iostream>
#include<queue>
using namespace std;
char solve(queue<char> &qu,int k)
{queue<char> temp;char e;for(int i=0;i<k-1;i++){temp.push(qu.front());qu.pop();}e=qu.front();qu.pop();while(!qu.empty()){temp.push(qu.front());qu.pop();}qu=temp;return e;
}
int main()
{queue<char> qu;qu.push('a');qu.push('b');qu.push('c');qu.push('d');int k=3;char e=solve(qu,k);cout<<"出队元素是"<<e<<endl;cout<<"出队顺序是:";while(!qu.empty()){cout<<qu.front()<<" ";qu.pop();}cout<<endl;return 0;
}
二、递归算法
-
- 递归实现简单选择排序
#include<iostream>
using namespace std;
void SelectSort(int a[], int n, int i)
{ int j, k;if (i==n-1) return; //满足递归出口条件else{k=i; //k记录a[i..n-1]中最小元素的下标for (j=i+1;j<n;j++) //在a[i..n-1]中找最小元素if (a[j]<a[k])k=j;if (k!=i) //若最小元素不是a[i]swap(a[i],a[k]); //a[i]和a[k]交换SelectSort(a,n,i+1);}
}
int main()
{int a[10]={5,4,6,2,1,0,3,8,7,9};SelectSort(a,10,0);for(int i=0;i<10;i++)cout<<a[i]<<' ';}
-
- 递归实现冒泡排序
#include<iostream>
using namespace std;
void BubbleSort(int a[], int n,int i)
{ int j;bool exchange;if (i==n-1) return; //满足递归出口条件else{exchange=false; //置exchange为falsefor(j=n-1;j>i;j--)if(a[j]<a[j-1]) //当相邻元素反序时{swap(a[j],a[j-1]);exchange=true; //发生交换置exchange为true}if(exchange==false) //未发生交换时直接返回 return ;else //发生交换时继续递归调用BubbleSort(a,n,i+1); }
}
int main()
{int a[10]={5,4,6,2,1,0,3,8,7,9};BubbleSort(a,10,0);for(int i=0;i<10;i++)cout<<a[i]<<' ';}
-
- 应用递归算法求解逆置单链表问题
【问题描述】对于不带头结点的单链表L,设计一个递归算法逆置所有结点。编写完整的实验程序,并采用相应数据进行测试。
- 应用递归算法求解逆置单链表问题
#include<iostream>
#include<list>
#include<malloc.h>
using namespace std;
typedef int ElemType;
typedef struct Node
{ ElemType data;struct Node *next;
} LinkNode;
void CreateList(LinkNode *&L,ElemType a[],int n) //由a[0..n-1]创建单链表L
{LinkNode *p, *r;L=(LinkNode *)malloc(sizeof(LinkNode));L->data=a[0];r=L; //r指向当前尾结点for (int i=1;i<n;i++){p=(LinkNode *)malloc(sizeof(LinkNode));p->data=a[i];r->next=p;r=p;}r->next=NULL; //尾结点next域置为空
}
void DispList(LinkNode *L) //输出单链表L
{LinkNode *p=L;while (p!=NULL){cout<<p->data<<" ";p=p->next;}cout<<endl;
}
LinkNode *Reverse(LinkNode *L) //逆置不带头结点的单链表L
{ LinkNode *p;if (L==NULL || L->next==NULL)return L;p=Reverse(L->next);L->next->next=L; //将L结点链接到L->next结点后面L->next=NULL; //将L结点作为整个逆置后的尾结点return p;
}
int main()
{ElemType a[]={1,2,3,4,5,6};int n=sizeof(a)/sizeof(a[0]);LinkNode *L;CreateList(L,a,n);cout<<"实验结果:"<<endl;cout<<" 逆置前L: "<<endl;DispList(L);cout<<" 执行L=Reverse(L)"<<endl;L=Reverse(L);cout<<" 逆置后L: "<<endl;DispList(L);return 0;
}
三、分治法
-
- 分治法进行快排
#include<iostream>
using namespace std;
int Partition(int a[],int s,int t) //划分算法
{ int i=s,j=t;int temp=a[s]; //用序列的第1个记录作为基准while(i!=j){while(j>i&&a[j]>=temp)j--; //从右向左扫描,找第1个关键字小于tmp的a[j]a[i]=a[j]; //将a[j]前移到a[i]的位置while(i<j&&a[i]<temp)i++;//从左向右扫描,找第1个关键字大于tmp的a[i]a[j]=a[i]; //将a[i]后移到a[j]的位置}a[i]=temp;return i;
}
void QuickSort(int a[],int s,int t)
//对a[s..t]元素序列进行递增排序
{ if (s<t) //序列内至少存在2个元素的情况{ int i=Partition(a,s,t);QuickSort(a,s,i-1); //对左子序列递归排序QuickSort(a,i+1,t); //对右子序列递归排序}
}
int main()
{int a[10]={5,4,6,2,10,0,3,8,7,9};QuickSort(a,0,10);for(int i=0;i<10;i++){cout<<a[i]<<" ";}cout<<endl;return 0;
}
-
- 分治法进行归并排序
#include<iostream>
#include<algorithm>
#include<malloc.h>
using namespace std;
void Merge(int a[],int low,int mid,int high)
{int *tmpa;int i=low,j=mid+1,k=0;tmpa=(int *)malloc((high-low+1)*sizeof(int));while(i<=mid&&j<=high)if(a[i]<=a[j]) //将第1子表中的元素放入tmpa中{tmpa[k]=a[i]; i++; k++;}else //将第2子表中的元素放入tmpa中{tmpa[k]=a[j];j++;k++;}while (i<=mid) //将第1子表余下部分复制到tmpa{ tmpa[k]=a[i]; i++; k++; }while (j<=high) //将第2子表余下部分复制到tmpa{ tmpa[k]=a[j]; j++; k++; }for(k=0,i=low;i<=high;k++,i++) //将tmpa复制回a中a[i]=tmpa[k];free(tmpa); //释放tmpa所占内存空间
}
//一趟二路归并排序
void MergePass(int a[],int length,int n)
{int i;for(i=0;i+2*length-1<n;i=i+2*length) //归并length长的两相邻子表Merge(a,i,i+length-1,i+2*length-1);if(i+length-1<n) //余下两个子表,后者长度小于lengthMerge(a,i,i+length-1,n-1); //归并这两个子表
}
void MergeSort(int a[],int n) //二路归并算法
{ int length;for (length=1;length<n;length=2*length)MergePass(a,length,n);
}
int main()
{int a[]={2,5,1,7,10,6,9,4,3,8};MergeSort(a,10);for(int i=0;i<10;i++){cout<<a[i]<<" ";}cout<<endl;return 0;
}
-
- 分治法进行折半查找
#include<iostream>
#include<algorithm>
using namespace std;
int BinSearch(int a[],int low,int high,int k)
//拆半查找算法
{int mid;if(low<high){mid=(low+high)/2;if(a[mid]==k)return mid;if(a[mid]>k)return BinSearch(a,low,mid-1,k);elsereturn BinSearch(a,mid+1,high,k);}return -1;
}
int main()
{int i;int k=2;int a[]={1,2,3,4,5,6,7,8,9,10};i=BinSearch(a,0,9,k);if(i!=-1){cout<<"找到,位置是:"<<i<<endl;}else cout<<"未找到"<<endl;return 0;
}
-
- 应用递归和分治法求解众数问题
【问题描述】给定含有n个元素的多重集合S,每个元素在S中出现的次数称为该元素的重数。多重集S中重数最大的元素称为众数。 例如,S={1,2,2,2,3,5}。 多重集S的众数是2,其重数为3。 对于给定的由n 个自然数组成的多重集S,编程计算S 的众数及其重数。
- 应用递归和分治法求解众数问题
#include <iostream>
#include<algorithm>
using namespace std;
#define M 100
int a[M];
int num,val,n; //重数, 众数,个数
void find(int &l,int &r,int mid)//找中位数的最左,最右边界位置
{l = r= mid;while(a[l]==a[mid] && l>= 0) --l;l++; //还原while(a[r]==a[mid] && r<= n-1) ++r;r--;
}
void Fun(int low,int high)
{if(low > high) return; //左右边界交叉,结束int mid = (low + high)/2; //中位数int i,j;find(i,j,mid);if(j-i+1 > num){ //更新num = j-i+1;val = a[mid];}if(i-low > num){//分治递归Fun(low,i-1);}if(high -j > num){Fun(j+1,high);}
}
int main()
{int i;cout<<"输入元素个数:\n";cin>>n;cout<<"输入元素:\n";for(i=0;i<n;i++)cin>>a[i];sort(a,a+n);for(i=0;i<n;i++)cout<<a[i]<<",";Fun(0,n-1);cout<<endl<<"众数:"<<val<<" 重数:"<<num;return 0;
}
四、蛮力法
-
- 蛮力法解决简单选择排序
#include<iostream>
using namespace std;
void SelectSort(int a[],int n)
//对a[0..n-1]元素进行递增简单选择排序
{ int i,j,k;for (i=0;i<n-1;i++) //进行n-1趟排序{ k=i; //用k记录每趟无序区中最小元素的位置for (j=i+1;j<n;j++) //在a[i+1..n-1]中穷举找最小元素a[k]if (a[j]<a[k]) k=j; if (k!=i) //若a[k]不是最小元素,将a[k]与a[i]交换swap(a[i],a[k]);}
}
int main()
{int a[]={5,9,4,2,1};SelectSort(a,5);for(int i=0;i<5;i++){cout<<a[i]<<" ";}
}
-
- 蛮力法解决冒泡排序
#include<iostream>
using namespace std;
void BubbleSort(int a[],int n)
//对a[0..n-1]按递增有序进行冒泡排序
{ int i,j; int tmp;bool exchange;for (i=0;i<n-1;i++) //进行n-1趟排序{ exchange=false; //本趟排序前置exchange为falsefor (j=n-1;j>i;j--) //无序区元素比较,找出最小元素if (a[j]<a[j-1]) //当相邻元素反序时{ swap(a[j],a[j-1]); //a[j]与a[j-1]进行交换exchange=true; //发生交换置exchange为true}if (exchange==false) //本趟未发生交换时结束算法return;}
}
int main()
{int a[]={5,9,4,2,1};BubbleSort(a,5);for(int i=0;i<5;i++){cout<<a[i]<<" ";}
}
-
- 应用蛮力法求解钱币兑换问题
【问题描述】某个国家仅有1分、2分和5分硬币,将钱n(n>=5)兑换成硬币有很多种兑法。编写一个实验程序计算出10分钱有多少种兑法,并列出每种兑换方式。
- 应用蛮力法求解钱币兑换问题
#include<iostream>
using namespace std;
int main()
{int n=10;int x,y,z;int num=0;for(z=0;z<=2;z++){for(y=0;y<=5;y++){for(x=0;x<=10;x++){if(z*5+y*2+x*1==10){cout<<"兑换方式"<<++num; if(z!=0) cout<<" 5分的硬币有:"<<z<<"个"; if(y!=0) cout<<" 2分的硬币有:"<<y<<"个"; if(x!=0) cout<<" 1分的硬币有:"<<x<<"个"; cout<<endl;}}}}cout<<"共有"<<num<<"种兑换方式"<<endl; return 0;
}
五、回溯法
-
- 回溯法求解求解0/1背包问题
#include <iostream>
using namespace std;
#define MAXN 20//问题表示
int n=4; //4种物品
int W=6; //限制重量为6
int w[]={0,5,3,2,1}; //存放4个物品重量,不用下标0元素
int v[]={0,4,4,3,1}; //存放4个物品价值,不用下标0元素
//求解结果表示
int x[MAXN]; //存放最终解
int maxv; //存放最优解的总价值void dfs(int i,int tw,int tv,int rw,int op[])
{ if (i>n) //找到一个叶子结点{ if (tw==W && tv>maxv) //找到一个满足条件的更优解,保存{ maxv=tv;for (int j=1;j<=n;j++)x[j]=op[j];}}else //尚未找完所有物品{if ( tw+w[i]<=W ) //左孩子结点剪枝{ op[i]=1; //选取第i个物品dfs(i+1,tw+w[i],tv+v[i],rw-w[i],op);}if ( tw+rw-w[i]>=W ) //右孩子结点剪枝{ op[i]=0; //不选取第i个物品,回溯dfs(i+1,tw,tv,rw-w[i],op);}}
}int main()
{int op[MAXN];dfs(1,0,0,11,op);cout<<"最优值是:"<<maxv<<endl;for(int j=1;j<=n;j++)cout<<x[j]<<" ";
}
-
- 应用回溯法求解组合问题
【问题描述】编写一个实验程序,采用回溯法输出自然数1~n中任取r个数的所有组合。
- 应用回溯法求解组合问题
#include <iostream>
#include <vector>
using namespace std;
int n,r;
void disp(vector<int> path)
{for(int j=0;j<path.size();j++)cout<<path[j]<<" ";cout<<endl;
}
void dfs(vector<int> path,int i,int num)
{if(num==r)disp(path);for(int j=i;j<=n;j++){path.push_back(j);dfs(path,j+1,num+1);path.pop_back();}
}
int main()
{cin>>n>>r;vector<int> path;dfs(path,1,0);return 0;
}
六、分支限界法
- 应用分枝限界法求解n皇后问题
【问题描述】在n×n的方格棋盘上,放置n个皇后,要求每个皇后不同行、不同列、不同左右对角线。如图1所示是6皇后问题的一个解。要求采用队列式分枝限界法求解4皇后问题的一个解,并分析对应程序运行中创建的队列结点的个数。
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int n=4;
int Count=1;
struct NodeType
{int no;int row;vector<int> cols;
};
void dispnode(NodeType e)
{if(e.row!=-1)cout<<"编号"<<e.no<<"对应位置是:"<<e.row<<","<<e.cols[e.row]<<endl;elsecout<<"编号"<<e.no<<"对应位置是:"<<e.row<<","<<"*"<<endl;
}
bool Valid(vector <int> cols,int i,int j)
{int k=0;while(k<i){if((cols[k]==j)||(abs(cols[k]-j)==abs(k-i))) return false;k++;}return true;
}
void solve()
{int i,j;NodeType e,el;queue<NodeType> qu;e.no=Count++;e.row=-1;qu.push(e);cout<<"进队:";dispnode(e);while(!qu.empty()){e=qu.front();qu.pop();cout<<"出队";dispnode(e);if(e.row==n-1){cout<<"产生一个解:";for(int i=0;i<n; i++){cout<<i+1<<","<<e.cols[i]+1<<" ";}cout<<endl;return ;}else{for(j=0;j<n;j++){i=e.row+1;if(Valid(e.cols,i,j)){el.no=Count++;el.row=i;el.cols=e.cols;el.cols.push_back(j);qu.push(el);cout<<"进队子结点:";dispnode(el);}}}}
}
int main()
{solve();return 0;
}
七、贪心法
-
- 贪心算法求解活动安排问题
#include <iostream>
#include<string.h>
#include<algorithm>
using namespace std;
#define MAX 51
//问题表示
struct Action //活动的类型声明
{ int b; //活动起始时间int e; //活动结束时间bool operator<(const Action &s) const //重载<关系函数{return e<=s.e; //用于按活动结束时间递增排序}
};
int n=11;
Action A[]={{0},{1,4},{3,5},{0,6},{5,7},{3,8},{5,9},{6,10},{8,11},{8,12},{2,13},{12,15}}; //下标0不用
//求解结果表示
bool flag[MAX]; //标记选择的活动
int Count=0;
void solve() //求解最大兼容活动子集
{ memset(flag,0,sizeof(flag)); //初始化为falsesort(A+1,A+n+1); //A[1..n]按活动结束时间递增排序int preend=0; //前一个兼容活动的结束时间for (int i=1;i<=n;i++) //扫描所有活动{ if (A[i].b>=preend) //找到一个兼容活动{ flag[i]=true; //选择A[i]活动preend=A[i].e; //更新preend值}}
}
int main()
{solve();cout<<"求解结果,选取的活动:"<<endl;for (int i=1;i<=n;i++) //求v/wif(flag[i]){cout<<A[i].b<<","<<A[i].e<<endl;Count++;}cout<<"共有"<<Count<<"个活动";return 0;
}
-
- 应用贪心法求解删数问题
【问题描述】编写一个实验程序实现求解删数问题。给定共有n位的正整数d,去掉其中任意,k<=n个数字后剩下的数字按原次序排列组成一个新的正整数。对于给定的n位正整数d和正整数k,找出剩下数字组成的新数最小的删数方案。
- 应用贪心法求解删数问题
#include <iostream>
#include <string>
using namespace std;
int main()
{string N;int k,i;cin >> N >> k;while (k--){int len=N.length();for (i=0;i<len-1;i++)if (N[i]>N[i+1]){N.erase(N.begin()+i);break;}if (i==len-1)N.erase(N.end()-1); //删除最后数字}while(N[0]=='0'&&N.length()>1)N.erase(N.begin());cout << N << endl;return 0;
}
八、动态规划
-
- 动态规划求解最大连续子序列和问题
#include<iostream>
using namespace std;
int a[]={0,-2,11,-4,13,-5,-2};
int n=6;
int dp[20];
void maxsubsum()
{dp[0]=0;for(int j=1;j<=n;j++)dp[j]=max(dp[j-1]+a[j],a[j]);
}
void dispmaxsum()
{int maxj=1;for(int j=1;j<=n;j++)if(dp[j]>dp[maxj]) maxj=j;int k;for(k=maxj;k>=1;k--)if(dp[k]<=0) break;cout<<dp[maxj]<<endl;for(int i=k+1;i<=maxj;i++)cout<<a[i]<<" ";
}
int main()
{maxsubsum();dispmaxsum();return 0;
}
-
- 应用动态规划算法求解矩阵最小路径和问题
【问题描述】给定一个m行n列的矩阵,从左上角开始每次只能向右或者向下移动,最后到达右下角的位置,路径上的所有数字累加起来作为这条路径的路径和。编写一个实验程序求所有路径和中的最小路径和。例如,以下矩阵中的路径1→3→1→0→6→1→0是所有路径中路径和最小的,返回结果是12:
- 应用动态规划算法求解矩阵最小路径和问题
1 3 5 98 1 3 45 0 6 18 8 4 0
#include<iostream>
#include<vector>
#include<stdio.h>
using namespace std;
#define MAXM 100
#define MAXN 100
//问题表示
int a[MAXM][MAXN]={{1,3,5,9},{8,1,3,4},{5,0,6,1},{8,8,4,0}};
int m=4,n=4;
//求解结果表示
int ans; //最小路径长度
int dp[MAXM][MAXN];
int pre[MAXM][MAXN];
void Minpath() //求最小和路径ans
{ int i,j;dp[0][0]=a[0][0];for(i=1;i<m;i++) //计算第一列的值{ dp[i][0]=dp[i-1][0]+a[i][0];pre[i][0]=0; //垂直路径}for(j=1;j<n;j++) //计算第一行的值{ dp[0][j]=dp[0][j-1]+a[0][j];pre[0][j]=1; //水平路径}for(i=1;i<m;i++) //计算其他dp值for(j=1;j<n;j++){ if (dp[i][j-1]<dp[i-1][j]){ dp[i][j]=dp[i][j-1]+a[i][j];pre[i][j]=1;}else{ dp[i][j]=dp[i-1][j]+a[i][j];pre[i][j]=0;}}ans=dp[m-1][n-1];
}
void Disppath() //输出最小和路径
{ int i=m-1,j=n-1;vector<int> path; //存放反向最小路径vector<int>::reverse_iterator it;while (true){ path.push_back(a[i][j]);if (i==0 && j==0) break;if (pre[i][j]==1) j--; //同行else i--; //同列}printf(" 最短路径: ");for (it=path.rbegin();it!=path.rend();++it)printf("%d ",*it); //反向输出构成正向路径printf("\n 最短路径和:%d\n",ans);
}
int main()
{Minpath(); //求最小路径和printf("求解结果\n");Disppath(); //输出求最小路径与最小路径和return 0;
}
相关文章:

【算法设计与分析】STL容器、递归算法、分治法、蛮力法、回溯法、分支限界法、贪心法、动态规划;各类算法代码汇总
文章目录前言一、STL容器二、递归算法三、分治法四、蛮力法五、回溯法六、分支限界法七、贪心法八、动态规划前言 本篇共为8类算法(STL容器、递归算法、分治法、蛮力法、回溯法、分支限界法、贪心法、动态规划),则各取每类算法中的几例经典示例进行展示。 一、STL容…...
vue初识
第一次接触vue,前端的html,css,jquery,js学习也有段时间了,就照着B站的视频简单看了一些,了解了一些简单的用法,这边做一个记录。 官网 工具:使用VSCode以及Live Server插件(能够实时预览) 第…...

火山引擎入选《2022 爱分析 · DataOps 厂商全景报告》,旗下 DataLeap 产品能力获认可
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 2 月 9 日,国内领先的数字化市场研究与咨询机构爱分析发布了《2022 爱分析DataOps 厂商全景报告》(以下简称报告),报…...

java-spring_bean的生命周期
生命周期:从创建到消亡的完整过程初始化容器 1. 创建对象(内存分配 ) 2. 执行构造方法 3. 执行属性注入(set操作) 4. 执行bean初始化方法 使用bean 执行业务操作 关闭/销毁容器 1.执行bean销毁方法 bean销毁时机 容…...
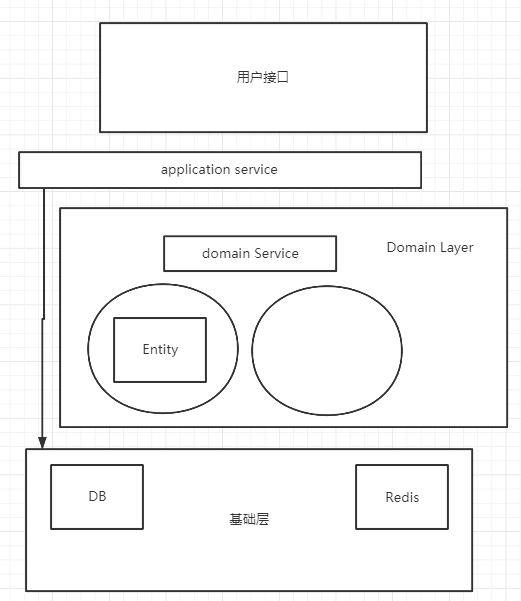
微服务相关概念
一、谈谈你对微服务的理解,微服务有哪些优缺点?微服务是由Martin Fowler大师提出的。微服务是一种架构风格,通过将大型的单体应用划分为比较小的服务单元,从而降低整个系统的复杂度。优点:1、服务部署更灵活࿱…...
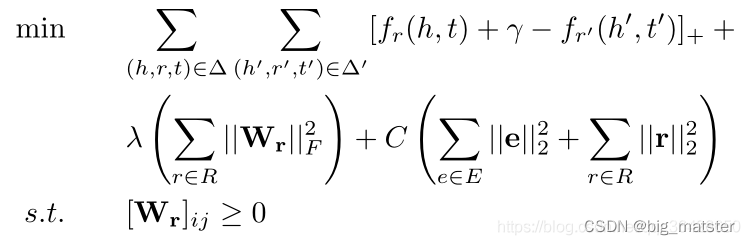
论文解读:(TransA)TransA: An Adaptive Approach for Knowledge Graph Embedding
简介 先前的知识表示方法:TransE、TransH、TransR、TransD、TranSparse等。的损失函数仅单纯的考虑hrh rhr和ttt在某个语义空间的欧氏距离,认为只要欧式距离最小,就认为h和th和th和t的关系为r。显然这种度量指标过于简单,虽然先…...

js将数字转十进制+十六进制(联动el-ui下拉选择框)
十进制与十六进制的整数转化一、十进制转十六进制二、十六进制转十进制三、联动demo一、十进制转十六进制 正则表达式: /^([0-9]||([1-9][0-9]{0,}))$/解析:[0-9]代表个位数,([1-9][0-9]{0,})代表十位及以上 二、十六进制转十进制 正则表达…...

关于RedissonLock的一些所思
关于RedissonClient.getLock() 我们一般的使用Redisson的方式就是: RLock myLock redissonClient.getLock("my_order");//myLock.lock();//myLock.tryLock();就上面的例子里,如果某个线程已经拿到了my_order的锁,那别的线程调用m…...

C++:倒牛奶问题
文章目录题目一、输入二、输出三、思路代码题目 农业,尤其是生产牛奶,是一个竞争激烈的行业。Farmer John发现如果他不在牛奶生产工艺上有所创新,他的乳制品生意可能就会受到重创! 幸运的是,Farmer John想出了一个好主…...
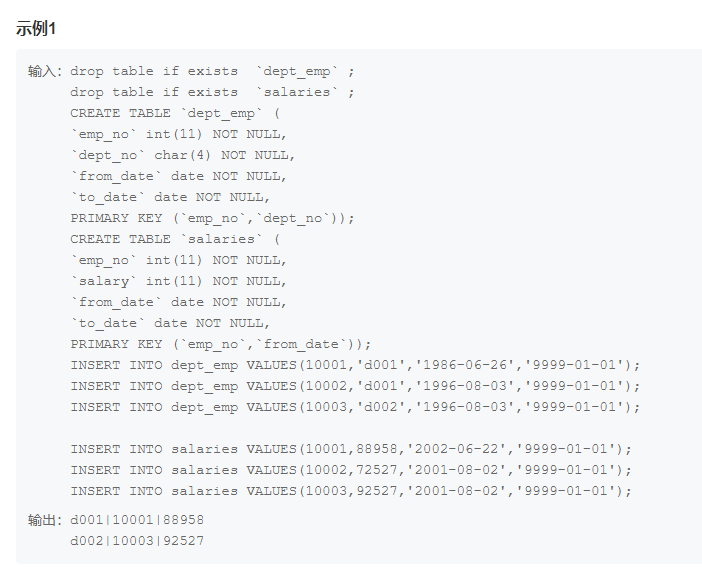
MySQL8.x group_by报错的4种解决方法
在我们使用MySQL的时候总是会遇到各种各样的报错,让人头痛不已。其中有一种报错,sql_modeonly_full_group_by,十分常见,每次都是老长的一串出现,然后带走你所有的好心情,如:LIMIT 0, 1000 Error…...

具有非线性动态行为的多车辆列队行驶问题的基于强化学习的方法
论文地址: Reinforcement Learning Based Approach for Multi-Vehicle Platooning Problem with Nonlinear Dynamic Behavior 摘要 协同智能交通系统领域的最新研究方向之一是车辆编队。研究人员专注于通过传统控制策略以及最先进的深度强化学习 (RL) 方法解决自动…...

TrueNas篇-硬盘直通
硬盘直通 在做硬盘直通之前,在trueNas(或者其他虚拟机)内是检测不到安装的硬盘的。 在pve节点查看硬盘信息 打开pve的shell控制台 输入下面的命令查看硬盘信息: ls -l /dev/disk/by-id/该命令会显示出实际所有的硬盘设备信息,其中ata代…...

手机子品牌的“性能战事”:一场殊途同归的大混战
在智能手机行业进入存量市场后,竞争更加白热化。当各国产手机品牌集体冲高端,旗下子品牌们也正厮杀正酣,显现出刀光剑影。处理器、屏幕、内存、价格等各方面无不互相对标,激烈程度并不亚于高端之争。源于OPPO的中端手机品牌realme…...
dockerfile自定义镜像安装jdk8,nginx,后端jar包和前端静态文件,并启动容器访问
dockerfile自定义镜像安装jdk8,nginx,后端jar包和前端静态文件,并启动容器访问简介centos7系统里面我准备的服务如下:5gsignplay-web静态文件内容如下:nginx.conf配置文件内容如下:Dockerfile内容如下:run.sh启动脚本内容如下:制作镜像并启动访问简介 通过用docker…...
MongoDB 全文检索
MongoDB 全文检索 全文检索对每一个词建立一个索引,指明该词在文章中出现的次数和位置,当用户查询时,检索程序就根据事先建立的索引进行查找,并将查找的结果反馈给用户的检索方式。 这个过程类似于通过字典中的检索字表查字的过…...

JS中声明变量,使用 var、let、const的区别
一、var 的使用 1.1、var 的作用域 1、var可以在全局范围声明或函数/局部范围内声明。当在最外层函数的外部声明var变量时,作用域是全局的。这意味着在最外层函数的外部用var声明的任何变量都可以在windows中使用。 2、当在函数中声明var时,作用域是局…...

汽车改装避坑指南:大尾翼
今天给大家讲一个改装的误区:大尾翼 很多车友看到一些汽车加了大尾翼,非常的好看,就想给自己的车也加装一个。 那你有没有想过,尾翼这东西你真的需要吗? 赛车为什么加尾翼?尾翼主要是给车尾部的一个压低提供…...

【Unity资源下载】POLYGON Dungeon Realms - Low Poly 3D Art by Synty
$149.99 Synty Studios 一个史诗般的低多边形资产包,包括人物、道具、武器和环境资产,用于创建一个以奇幻为主题的多边形风格游戏。 模块化的部分很容易在各种组合中拼凑起来。 包包含超过1,118个详细预制件。 主要特点 ◼ ◼ 完全模块化的地下城!包…...

知识汇总:Python办公自动化应该学习哪些内容
当前python自动化越来越受到欢迎,python一度成为了加班族的福音。还有大部分人想利用python自动化来简化工作,不知道从何处下手,所以,这里整理了一下python自动化过程中的各种办公场景以及需要用到的python知识点。 Excel办公自动…...

软件架构知识5-架构设计流程
一、识别复杂度 举例:设计一个亿级用户平台设计,直接对标腾讯的 QQ,按照腾讯 QQ的用户量级和功能复杂度进行设计,高性能、高可用、可扩展、安全等技术一应俱全,一开始就设计出了 40 多个子系统,然后投入大…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
