教你搞懂线段树,从基础到提高
秋名山码民的主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
🙏作者水平有限,如发现错误,还请私信或者评论区留言!
目录
- 前言
- 线段树逻辑概念
- 线段树的俩个重要用处
- 代码实现线段树
- 题目巩固
- 最后
前言
线段树算是比较难的一个数据结构,当时我高中提高组就没学懂,细数我学线段树也学了4遍,最早学的时候一脸懵逼,最近在刷题中发现其在蓝桥杯中也有考察,就寻思写一篇博客来巩固。
什么是线段树,线段树有什么用,线段树怎么写,能不能背过???
我认为对于打比赛的各位来说,线段树和前缀和一样,不能算做算法,它更多的是一种工具,一种时间复杂度为O(logn)的单点修改,区间查询的工具
线段树逻辑概念
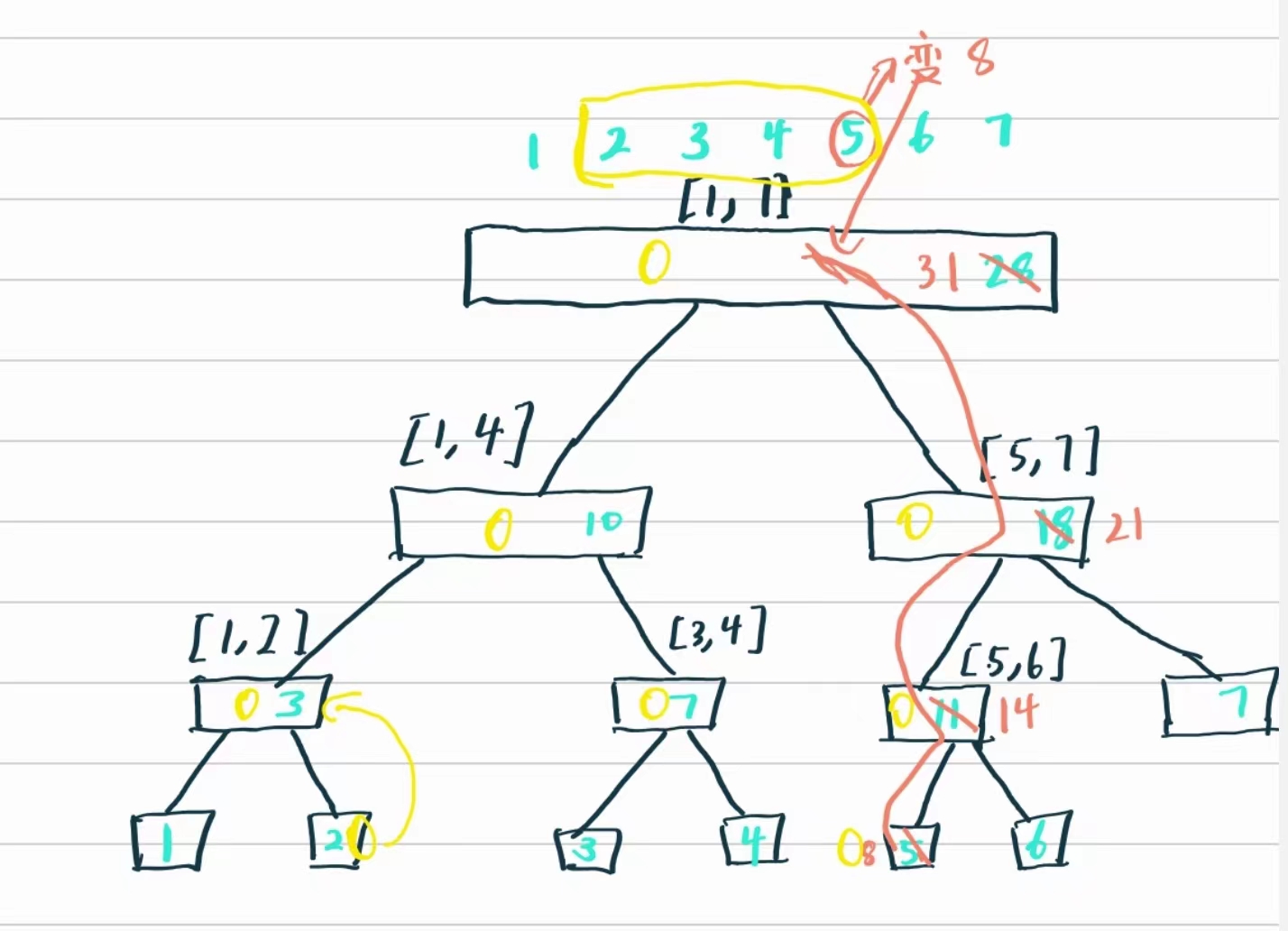
给定一个1~7的区间我们来维护它,将其转换为一个二叉树(线段树本身就是一个二叉树)
- 最上面的根的权值,为28,1~7的和
- 二叉树开分,左边为1~4的和为10,右边为5 ~ 6的和为21
- 1~4在开分,左边为3,右边为7 ,5 ~6开分,左边为14,右边为7
- 同上,直到不能再分
L,R:

class node{int l,r;int sum;
}
线段树的俩个重要用处
1. 单点修改
如上图我们将5变成8,其中要修改的为1~ 7,5~ 7,5~ 6,5,
2. 区间查询
如上图我们计算2 ~ 5区间,如果完全包含某个区间,则退出,否则进行递归,用黄圈表示需要递归的区间
- 1~7区间,递归左边,1 ~4区间,发现还没有被完全包含,进行左右俩边都递归,1 ~2,3 ~4,此刻,
3 ~4完全包含,不进行递归,继续递归1~ 2,2被完全包含 - 5~ 7区间,同上,进行递归
进行回溯区间,只算完全包含的区间,2+7+8 = 17
总结:
如果这个区间被完全包括在目标区间里面,直接返回这个区间的值
如果这个区间的左儿子和目标区间有交集,那么搜索左儿子
如果这个区间的右儿子和目标区间有交集,那么搜索右儿子
时间复杂度均为O(logn)
代码实现线段树
上面我们说线段树的俩个重要的用法,思考一下大概需要几个函数能实现?
- pushup:用子节点信息更新当前节点信息
- build:在一段区间上初始化线段树
- modify:修改
- query:查询
动态求连续区间和
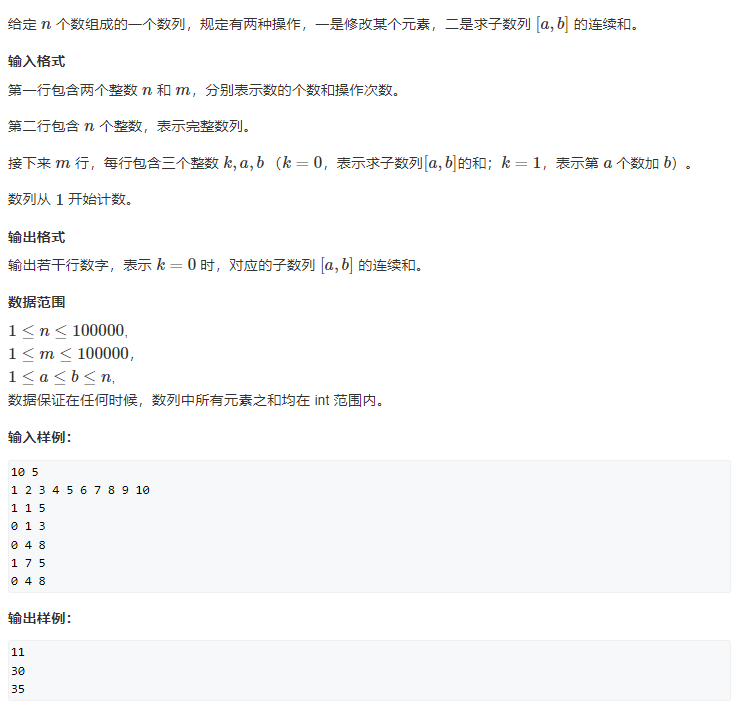
import java.io.*;/*** @Author 秋名山码神* @Date 2023/2/9* @Description*/
public class 动态求连续区间和 {static int n, k;static int[] a = new int[100100];static Node[] tr = new Node[400400];static class Node{int l, r, sum;Node(int l, int r, int sum) {this.l = l;this.r = r;this.sum = sum;}}public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));String[] cd = br.readLine().split(" ");n = Integer.parseInt(cd[0]);k = Integer.parseInt(cd[1]);String[] line = br.readLine().split(" ");for (int i=1;i<=n;i++)a[i] = Integer.parseInt(line[i-1]);build(1, 1, n);while (k-- > 0) {String[] li = br.readLine().split(" ");int k = Integer.parseInt(li[0]), l = Integer.parseInt(li[1]), r = Integer.parseInt(li[2]);if(k == 0) {bw.write(String.valueOf(query(1, l, r)));bw.write("\n");} elsemodify(1, l, r);}bw.flush();}static void pushUp(int u) {tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;}static void build(int u, int l, int r) {if(l == r) tr[u] = new Node(l , r, a[l]);else {tr[u] = new Node(l ,r, 0);int mid = l + r >> 1;build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);pushUp(u);}}static int query(int u, int l, int r) {if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;int mid = tr[u].l + tr[u].r >> 1, sum = 0;if(l <= mid) sum += query(u << 1, l, r);if(r > mid) sum += query(u << 1 | 1, l , r);return sum;}static void modify(int u, int x, int v) {if(tr[u].l == tr[u].r) tr[u].sum += v;else {int mid = tr[u].l + tr[u].r >> 1;if(x <= mid) modify(u << 1, x , v);else modify(u << 1 | 1, x, v);pushUp(u);}}
}题目巩固
区间和的个数
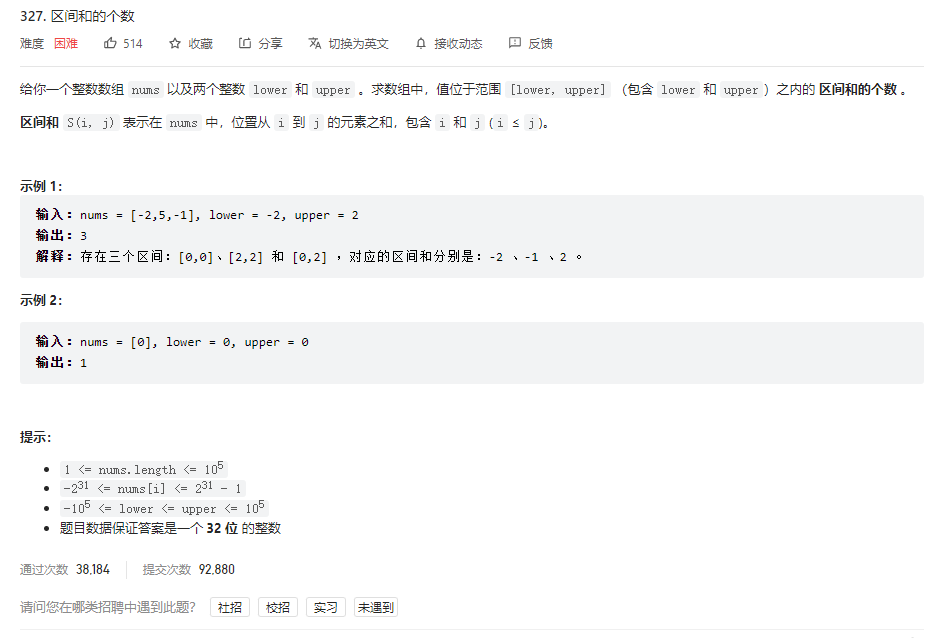
class Solution {public int countRangeSum(int[] nums, int lower, int upper) {int count = 0;int length = nums.length;long[] sums = new long[length + 1];for (int i = 0; i < length; i++) {sums[i + 1] = sums[i] + nums[i];}Set<Long> set = new HashSet<Long>();for (int i = 0; i <= length; i++) {long sum = sums[i];set.add(sum);set.add(sum - upper);set.add(sum - lower);}List<Long> sumsList = new ArrayList<Long>(set);Collections.sort(sumsList);Map<Long, Integer> ranks = new HashMap<Long, Integer>();int size = sumsList.size();for (int i = 0; i < size; i++) {ranks.put(sumsList.get(i), i);}SegmentTree st = new SegmentTree(size);for (int i = 0; i <= length; i++) {long sum = sums[i];int rank = ranks.get(sum);long minSum = sum - upper, maxSum = sum - lower;int start = ranks.get(minSum), end = ranks.get(maxSum);count += st.getCount(start, end);st.add(rank);}return count;}
}class SegmentTree {int length;int[] tree;public SegmentTree(int length) {this.length = length;this.tree = new int[length * 4];}public int getCount(int start, int end) {return getCount(start, end, 0, 0, length - 1);}public void add(int rank) {add(rank, 0, 0, length - 1);}private int getCount(int rangeStart, int rangeEnd, int index, int treeStart, int treeEnd) {if (rangeStart > rangeEnd) {return 0;}if (rangeStart == treeStart && rangeEnd == treeEnd) {return tree[index];}int mid = treeStart + (treeEnd - treeStart) / 2;if (rangeEnd <= mid) {return getCount(rangeStart, rangeEnd, index * 2 + 1, treeStart, mid);} else if (rangeStart > mid) {return getCount(rangeStart, rangeEnd, index * 2 + 2, mid + 1, treeEnd);} else {return getCount(rangeStart, mid, index * 2 + 1, treeStart, mid) + getCount(mid + 1, rangeEnd, index * 2 + 2, mid + 1, treeEnd);}}private void add(int rank, int index, int start, int end) {if (start == end) {tree[index]++;return;}int mid = start + (end - start) / 2;if (rank <= mid) {add(rank, index * 2 + 1, start, mid);} else {add(rank, index * 2 + 2, mid + 1, end);}tree[index] = tree[index * 2 + 1] + tree[index * 2 + 2];}
}
最后
看在博主这么努力,熬夜肝的情况下,给个免费的三连吧!

相关文章:

教你搞懂线段树,从基础到提高
秋名山码民的主页 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 🙏作者水平有限,如发现错误,还请私信或者评论区留言! 目录前言线段树逻辑概念线段树的俩个重要用处代码实现线段树题目巩固最后…...

C语言进阶——自定义类型:结构体
🌇个人主页:_麦麦_ 📚今日名言:生活不可能像你想象的那么好,也不会像你想象的那么糟。——莫泊桑《羊脂球》 目录 一、前言 二、正文 1结构体 1.1结构体的基础知识 1.2结构的声明 1.3特殊的声明 1.4结构体变量的…...

SpringSecurity学习笔记01
目录 一、课程介绍 二、框架概述 三、入门案例 四、基本原理(过滤器链) 五、基本原理(过滤器加载过程) 六、基本原理(两个重要的接口) 七、web权限方案-用户认证(设置用户名密码上) 八、…...
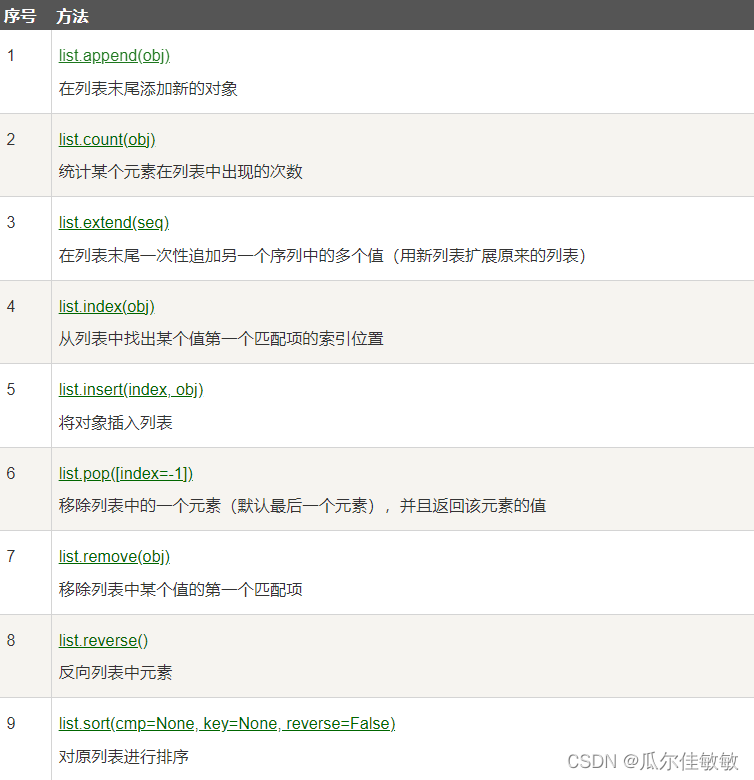
Python语言零基础入门教程(十一)
Python 列表(List) 序列是Python中最基本的数据结构。序列中的每个元素都分配一个数字 - 它的位置,或索引,第一个索引是0,第二个索引是1,依此类推。 Python有6个序列的内置类型,但最常见的是列表和元组。 序列都可以…...

现货白银基础知识
任何活动,任何项目,任何工作都离不开基础知识,这是肯定的。万丈高楼平地起,要想要简称百层高楼,首先得把低级打好!现货白银投资也是一样的道理,现在我们就来一起聊聊现货白银基础知识的问题&…...
数据库原理及应用基础知识点
数据库原理基础知识点大全数据库原理及应用1、数据库系统概述1.1 基本概念1.2 数据模型1.3 数据库系统的结构2、实体 -- 联系模型2.1 基本概念2.2 实体-联系图2.3 弱实体集3、关系数据模型3.1 关系数据库的结构3.2 从ER模型到关系模型3.3 关系操作、完整性约束、关系代数4、关系…...

【数据结构】栈(stack)
写在前面本篇文章开始讲解栈的有关知识,其实把顺序表和链表学好,那么这一章便不在话下,栈实际上就是顺序表或链表的一些特殊情况。用顺序表实现的栈叫做顺序栈用链表实现的栈叫做链栈文章的内容分为几个部分,希望读者能快速了解文…...
初识shell
文章目录一、shell基本知识1.1为什么学习和使用Shell编程1.2 什么是Shell1.2.1 shell的起源1.2.2 shell的功能1.3 shell的分类1.4 作为程序设计的语言——shell1.5 如何学好shell1.6 shell脚本的基本元素1.7 shell脚本编写规范1.8shell脚本的执行方式1.9 执行脚本的方法1.10 sh…...

程序员如何编写好开发技术文档 如何编写优质的API文档工作
编写技术文档,是令众多开发者望而生畏的任务之一。它本身是一件费时费力才能做好的工作。可是大多数时候,人们却总是想抄抄捷径,这样做的结果往往非常令人遗憾的,因为优质的技术文档是决定你的项目是否引人关注的重要因素。无论开…...

二级C语言操作例题(四十)
一、程序填空题 在此程序中,函数fun的功能是:在形参s所指字符串中寻找与参数c相同的字符,并在其后插入一个与之相同的字符,若找不到相同的字符则不做任何处理。 例如,若s所指字符串”baacda”,中c的字符为…...
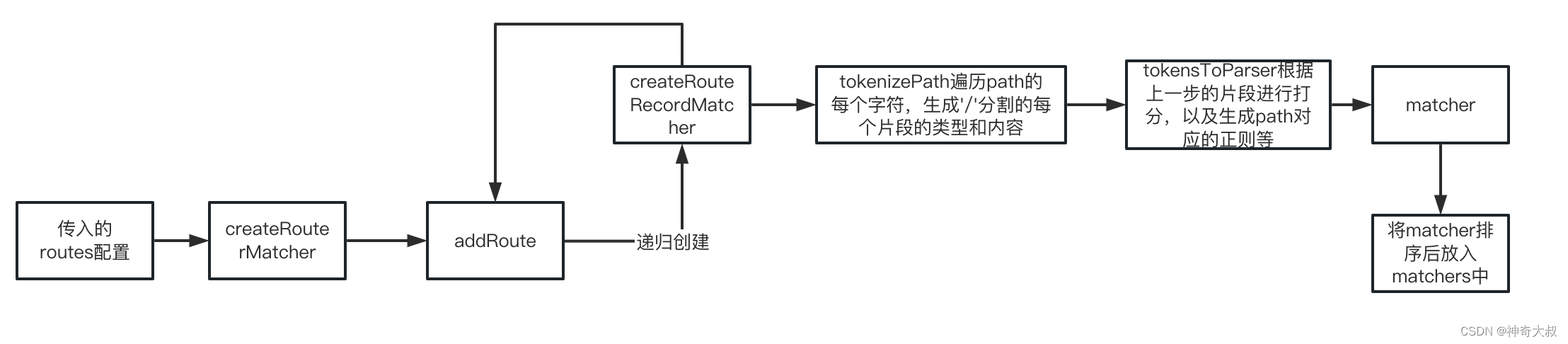
vue-router 源码解析(二)-创建路由匹配对象
文章目录基本使用导语createRouterMatcher 创建匹配路由记录addRoute 递归添加matchercreateRouteRecordMatcher 创建matchertokenizePath 解析pathtokensToParser 记录打分insertMatcher 将matcher排序总结基本使用 const routes [{path:"/",component: Demo2,nam…...

分布式新闻项目实战 - 10.Long类型精度丢失问题
怒发冲冠,凭阑处、潇潇雨歇。抬望眼,仰天长啸,壮怀激烈。三十功名尘与土,八千里路云和月。莫等闲、白了少年头,空悲切。 靖康耻,犹未雪。臣子恨,何时灭。驾长车,踏破贺兰山缺。壮志饥…...

如何将本地jar包安装到maven仓库
mvn install:install-file:主要是将本地自定义jar安装到maven仓库,然后在pom中可以直接通过dependency的方式来引用。 此命令有如参数: 命令说明-DgroupId自定义groupId设置groupId 名-DartifactId自定义artifactId设置该包artifactId名-Dversion自定义…...
C++:map和set的认识和简单使用/关联式容器
关联式容器 关联式容器即是用来存储数据的,并且存储的是<Key,Value>结构的键值对,在数据检索时效率比序列式容器高。 序列式容器也就是vector、list、queue等容器,因为其底层为线性序列的数据结构,里面存储的是…...

网络工程师一定要学会的知识点:OSPF,今天给大家详细介绍
1. OSPF 概念OSPF(Open Shortest Path First 开放式最短路径优先)是一种动态路由协议,属于内部网关协议(Interior Gateway Protocol,简称 IGP),是基于链路状态算法的路由协议。2. OSPF 的运行原理(1)OSPF 的…...
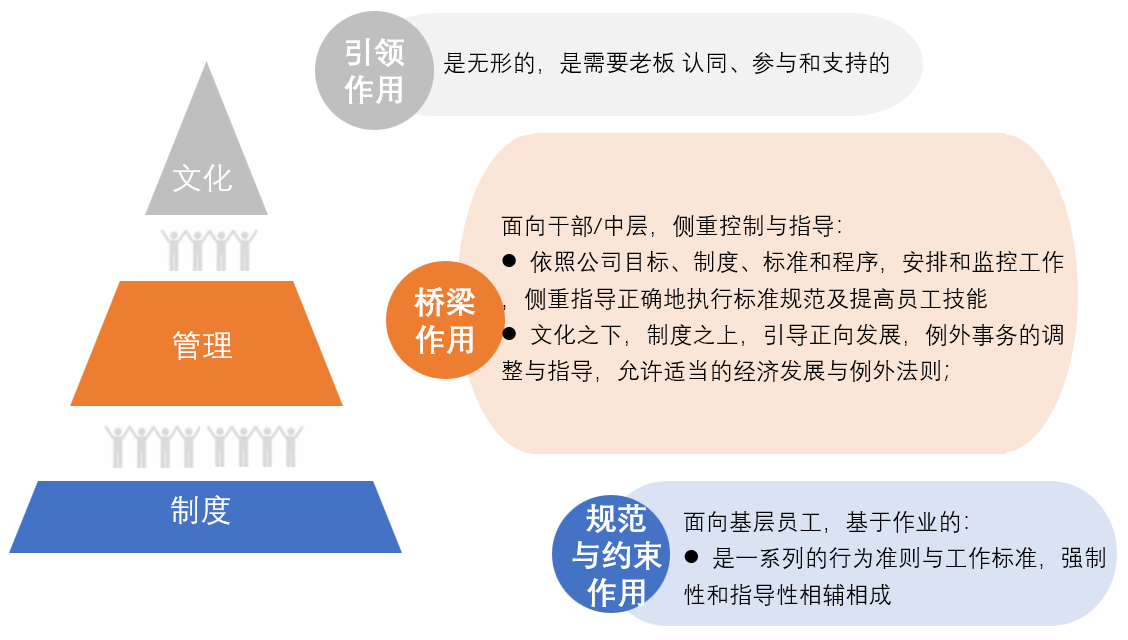
企业管理的三大基石及其关系
企业管理的三大基石三大基石是什么三大基石的关系制度:管理:文化:三大基石是什么 一个企业,不管它是属于哪种类型,影响员工行为的都有三种力量——制度、管理和文化,这是管理的三大基石。 三大基石的关系 …...

6个月软件测试培训出来后的感悟 —— 写给正在迷茫是否要转行或去学软件测试的学弟们
本人刚从某培训机构学习结束,现在已经上班一个月了。这篇文章我不会说太多的知识点,或噱人去培训机构学习的话语,仅作为一个普通打工者的身份,来写给那些对于软件测试未来发展、薪资待遇等不清楚的正在为家庭,解决信用…...

IoU Loss综述(IOU,GIOU,CIOU,EIOU,SIOU,WIOU)
边界框回归(BBR)的损失函数对于目标检测至关重要。它的良好定义将为模型带来显著的性能改进。大多数现有的工作假设训练数据中的样本是高质量的,并侧重于增强BBR损失的拟合能力。 一、L2-norm 最初的基于回归的BBR损失定义为L2-norm…...
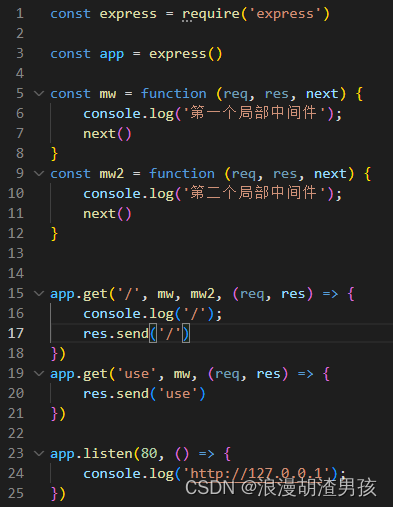
Node=>Express中间件 学习3
1.概念: 例:在处理污水的时候,一般都要经过三个处理环节,从而保证处理过后的废水,达到排放标准 处理污水的这三个中间处理环节,就可以叫中间件 2.中间件调用流程 当一个请求到达Express的服务器之后&#x…...
【STM32笔记】HAL库UART串口配置及重定向(解决接收中断与scanf不能同时工作的问题)
【STM32笔记】HAL库UART串口配置及重定向(解决接收中断与scanf不能同时工作的问题) 首先 要使用printf和scanf 必不可少的就是 #include <stdio.h>这里需要做的就是配置单片机的UART 并且使其能够被printf和scanf调用 打开异步工作模式 并且选择…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
