二进制枚举
一、左移:用来将一个数的各二进制位全部左移n位,低位以0补充,高位越界后舍弃。
n左移1位,n<<1,相当于2*n
1左移n位,1<<n,相当于2^n
二、右移:将一个数的各二进制位右移N位,移到右端的低位被舍弃,高位以符号位填充
n右移1位,n>>1,相当于|n/2|
x右移n位,x>>n,相当于|x/n|
三、常用操作
(n >> k) & 1,求n二进制下的第k位是0还是1,是1结果为真,是0结果为假。因为1的二进制数中只有第0位数是1,其余位数都是0。
n^=1,即n=n^1,能让n变成与原来相反的数(0或1)
n | (1 << k),能把n的第k位变成1
x=x&(x-1):用于消去x的最后一位
四、二进制状态压缩
二进制状态压缩是指讲一个长度为m的bool数组用一个m位二进制整数表示并存储的方法。利用下列位运算操作可以实现bool数组对应下标元素的存取。
取出整数n在二进制表示下的第k位 ( n >> k ) & 1
取出整数n在二进制表示下的第0~k-1位(后k位) n & ( ( 1 << k ) - 1 )
把整数n在二进制表示下的第k位取反 n ^ (1 << k)
对整数n在二进制表示下的第k位赋值1 n | ( 1 << k )
对整数n在二进制表示下的第k位赋值0 n & ( ~ ( 1 << k )
相关文章:

二进制枚举
一、左移:用来将一个数的各二进制位全部左移n位,低位以0补充,高位越界后舍弃。n左移1位,n<<1,相当于2*n1左移n位,1<<n,相当于2^n二、右移:将一个数的各二进制位右移N位&…...
2|数据挖掘|聚类分析|k-means/k-均值算法
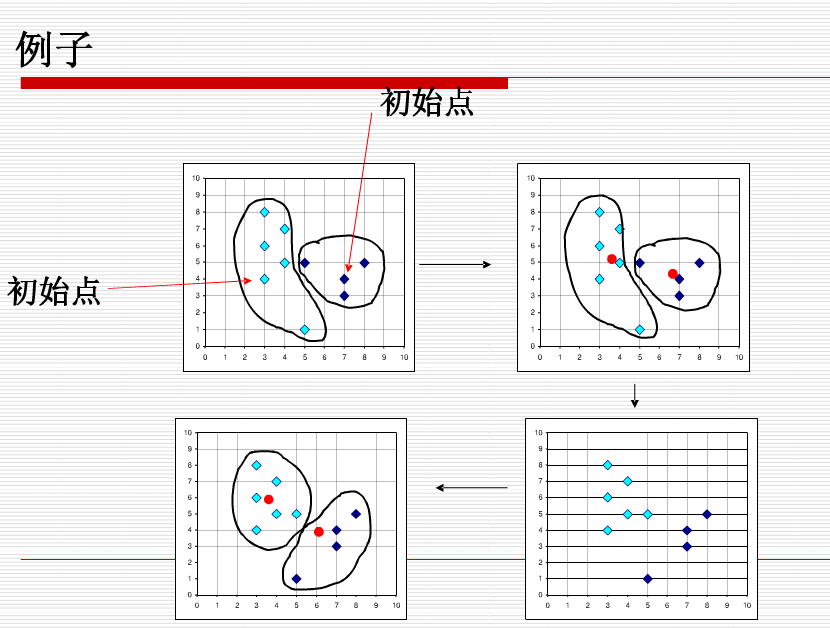
k-means算法k-means算法,也被称为k-平均或k-均值,是一种得到最广泛应用的聚类算法。算法首先随机选择k个对象,每个对象初始地代表了一个簇的平均值或中心。对剩余的每个对象根据其与各个簇中心的距离,将它赋给最近的簇。然后重新计…...
使用和制作动、静态库
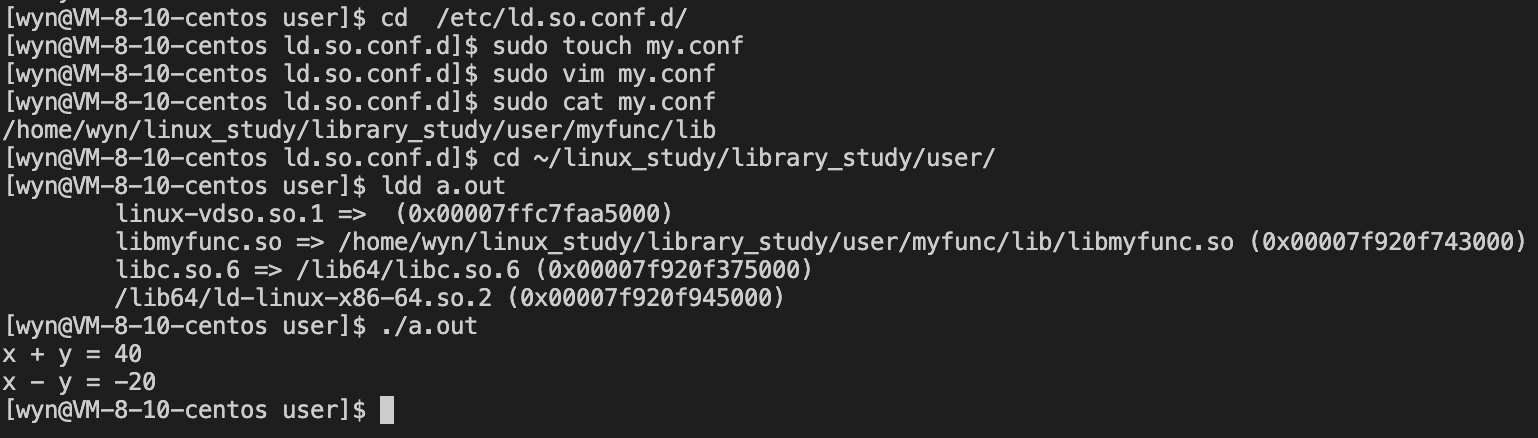
文章目录什么是库?静态库打包方式使用方式生成并执行可执行程序粗暴方式优化方式动态库不一样的.o文件打包方式使用方式生成可执行程序运行可执行程序无法运行时的解决方案动静态库与动静态链接什么是库? 从一开始的helloworld,到现在熟练使…...

【Java基础】023 -- 集合进阶(List、Set、泛型、树)
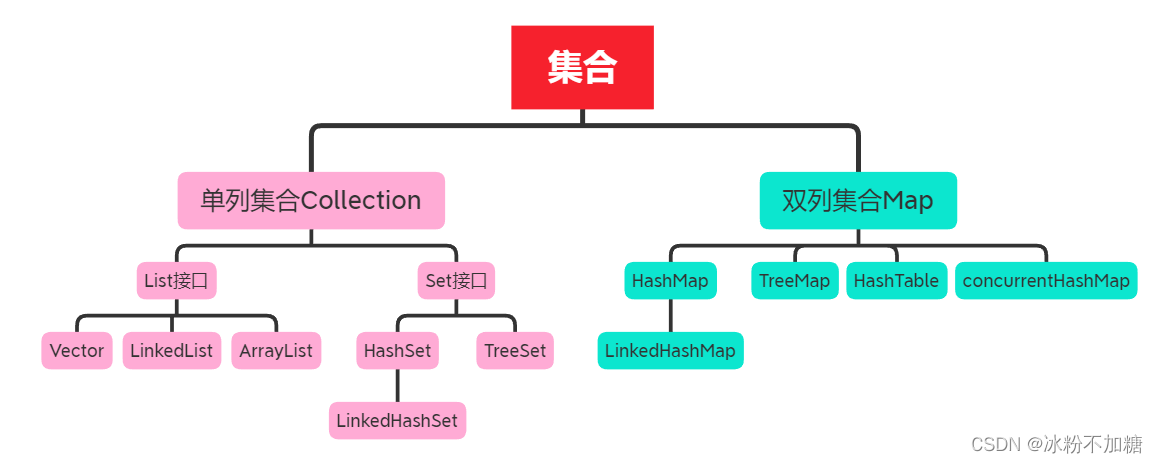
目录 一、集合的体系结构 1、单列集合(Collection) 二、Collection集合 1、Collection常见方法 ①、代码实现: ②、contains方法重写equals方法示例:(idea可自动重写) 2、Collection的遍历方式(…...
面试题整理01-集合详解
文章目录前言一、集合的整体结构单列集合接口:双列集合接口:二、单列集合详解1.List接口1.1 ArrayList集合特点:扩容:添加元素遍历1.2 LinkedList集合特点:添加元素:2.Set接口2.1 HashSet集合特点ÿ…...
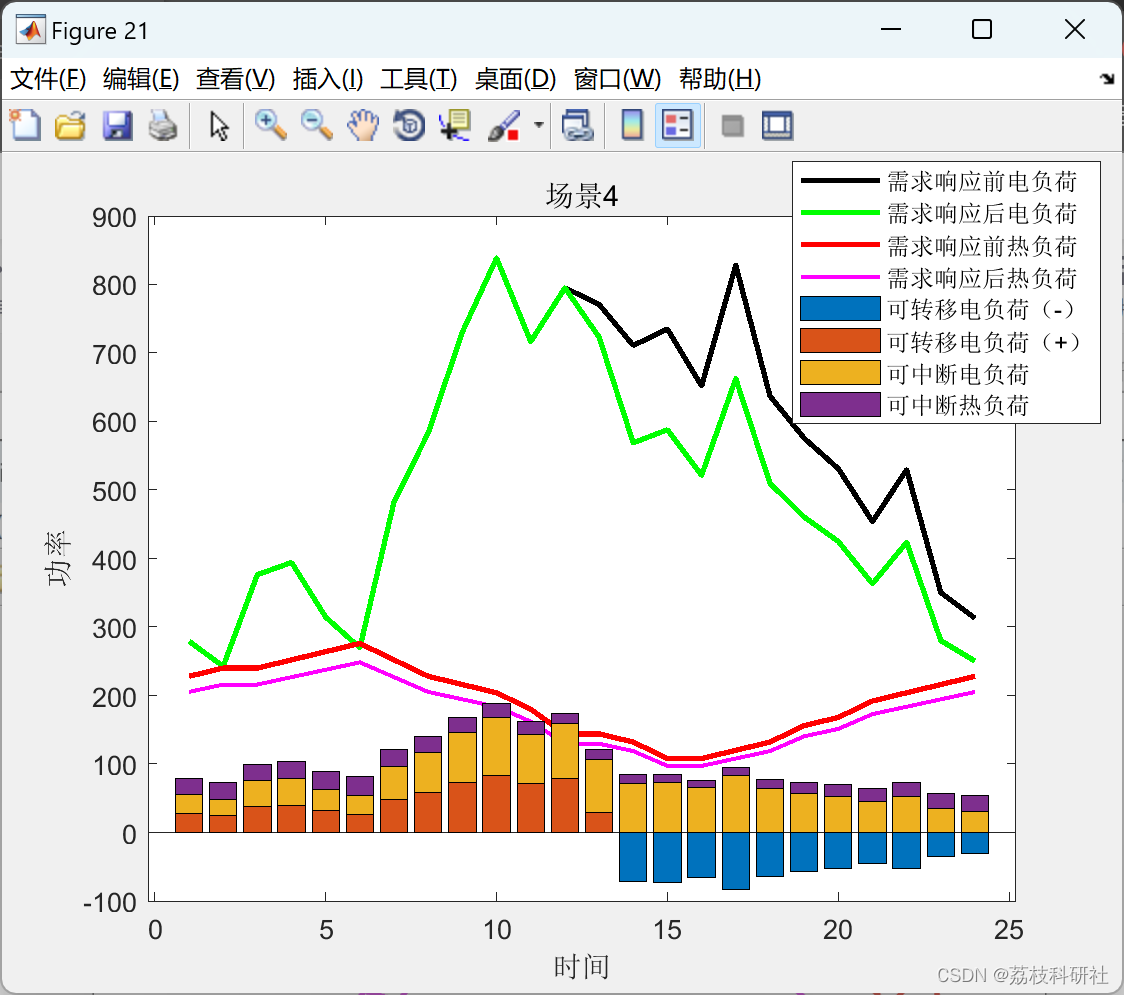
数据驱动的两阶段分布鲁棒(1-范数和∞-范数约束)的电热综合能源系统研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

ArcGIS网络分析之发布网络分析服务(二)
在上一篇中讲述了如何构建网络分析数据集,本篇将讲解如何发布网络分析服务。本文将使用上一篇中建立的网络数据集,下载地址在上一篇博文的最后已给出。 之前我们已经实现了基于ArcMap中的网络分析,但是仅仅支持本地是万万不够的,这里我们的目的就是将我们建好的网络分析图…...

js实现元素样式切换的基本功能
需求:用户第一次点击某些元素,改变元素的某些样式,比如背景颜色,字体颜色。用户第二次点击某些元素,恢复之前的样式。.....思路:准备一定量的div盒子,并取相同的类名<div class"box&quo…...

java 策略模式 + 工厂模式 实例
一 前言 经常听说各种设计模式,知道理论,也知道应该使用,但具体怎么用,什么时候用,使用的优点一直比较模糊,今天写一个项目中经常用到的模式,来具体理解。项目中经常用到工厂模式或者策略模式&…...
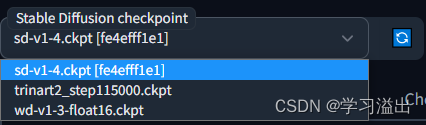
本地生成动漫风格 AI 绘画 图像|Stable Diffusion WebUI 的安装和部署教程
Stable Diffusion WebUI 的安装和部署教程1. 简介2. Windows安装环境3. 运行4. 模型下载链接5. 其他资源1. 简介 先放一张WebUI的图片生成效果图,以给大家学习的动力 :) 怎么样,有没有小小的心动?这里再补充一下&…...

华为OD机试 - 异常的打卡记录 | 备考思路,刷题要点,答疑 【新解法】
最近更新的博客 【新解法】华为OD机试 - 关联子串 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 停车场最大距离 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试 - 任务调度 | 备考思路,刷题要点,答疑,od Base 提供【新解法】华为OD机试…...
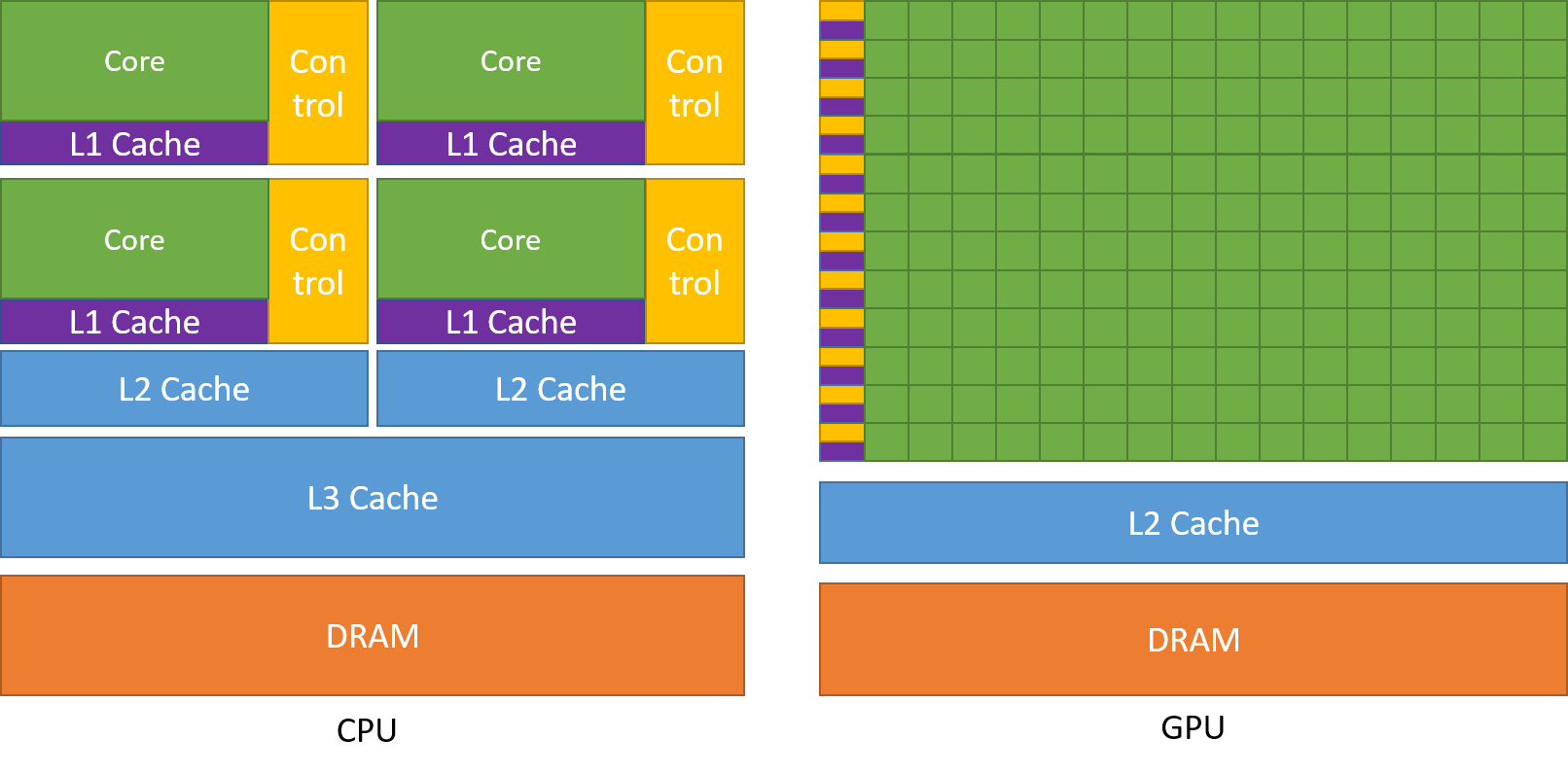
「机器学习笔记」之深度学习基础概念(基于Pytorch)
本文以 Pytorch 为线索,介绍人工智能和深度学习相关的一些术语、概念。 关于发展历史您也可以阅读深度学习神经网络之父 Jrgen Schmidhuber 所写的《Annotated History of Modern AI and Deep Learning(现代人工智能和深度学习的注释版历史)…...
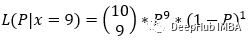
概率和似然
在日常生活中,我们经常使用这些术语。但是在统计学和机器学习上下文中使用时,有一个本质的区别。本文将用理论和例子来解释概率和似然之间的关键区别。 概率与似然 假设在一场棒球比赛中,两队的队长都被召集到场上掷硬币。获胜的队长将根据掷…...
前期软件项目评估偏差,如何有效处理?
1、重新评估制定延期计划 需要对项目进行重新评估,将新的评估方案提交项目干系人会议,开会协商一致后按照新的讨论结果制定计划,并实施执行。 软件项目评估偏差 怎么办:重新评估制定延期计划2、申请加资源 如果项目客户要求严格&a…...

Xline v0.2.0: 一个用于元数据管理的分布式KV存储
Xline是什么?我们为什么要做Xline? Xline是一个基于Curp协议的,用于管理元数据的分布式KV存储。现有的分布式KV存储大多采用Raft共识协议,需要两次RTT才能完成一次请求。当部署在单个数据中心时,节点之间的延迟较低&a…...

CompletableFuture
一、一个示例回顾Future 一些业务场景我们需要使用多线程异步执行任务,加快任务执行速度。JDK5新增了Future接口,用于描述一个异步计算的结果。虽然Future以及相关使用方法提供了异步执行任务的能力,但是对于结果的获取却是很不方便,我们必须使用Future.get()的方式阻塞调…...

面试不到10分钟就被赶出来了,问的实在是太变态了...
干了两年外包,本来想出来正儿八经找个互联网公司上班,没想到算法死在另一家厂子。 自从加入这家外包公司,每天都在加班,钱倒是给的不少,所以也就忍了。没想到11月一纸通知,所有人不许加班,薪资…...
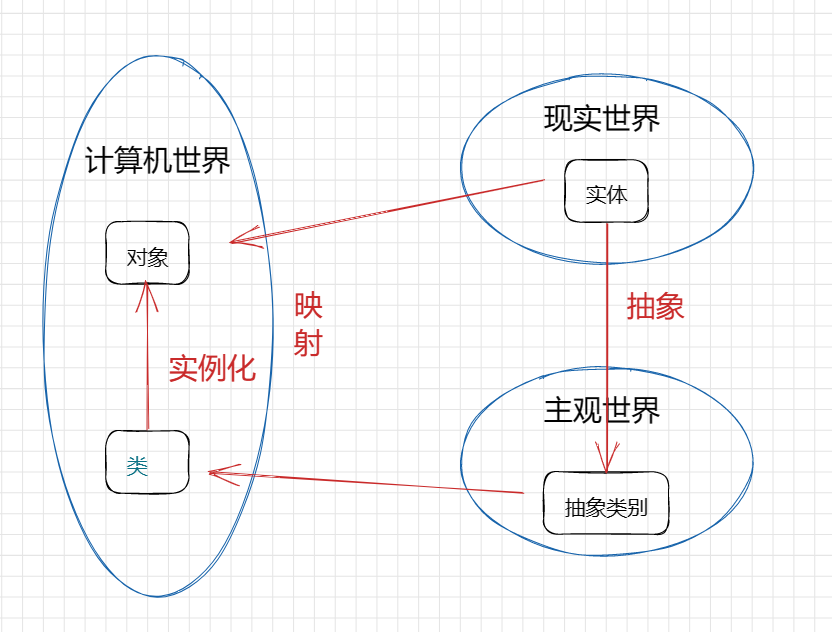
【C++】类与对象 (四)初始化列表 static成员 友元 内部类 匿名对象 拷贝对象时的一些编译器优化
前言 本章就是我们C中类与对象的终章了,不过本章的难度不大,都是类中一些边边角角的知识,记忆理解就行了,相信经过这么长时间的学习类与对象,你对面向对象也有了更加深的理解,最后我们学习完边边角角的一些…...

04:进阶篇 - 编译 CTK
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 在使用 CTK 之前,首先要进行编译。但要成功编译它,并不是一件很容易的事,这不仅取决于平台、Qt 的版本,也取决于编译器,以及所使用的 IDE。 平台(Linux、Windows)Qt 版本(4.x、5.x、6.x)编译器(MS…...

SQL73 返回所有价格在 3美元到 6美元之间的产品的名称和价格
描述有表Productsprod_idprod_nameprod_pricea0011egg3a0019sockets4b0019coffee15【问题】编写 SQL 语句,返回所有价格在 3美元到 6美元之间的产品的名称(prod_name)和价格(prod_price),使用 AND操作符&am…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
