LeetCode分类刷题----二叉树
二叉树
- 1.二叉树的递归遍历
- 144.二叉树的前序遍历
- 145.二叉树的后序遍历
- 94.二叉树的中序遍历
- 2.二叉树的迭代遍历
- 144.二叉树的前序遍历
- 145.二叉树的后序遍历
- 94.二叉树的中序遍历
- 3.二叉树的层序遍历
- 102.二叉树的层序遍历
- 107.二叉树的层序遍历||
- 199.二叉树的右视图
- 637.二叉树的层平均值
- 429.N叉树的层序遍历
- 515.在每个树行中找最大值
- 116.填充每个节点的下一个右侧节点指针
- 117.填充每个节点的下一个右侧节点指针||
- 104.二叉树的最大深度
- 111.二叉树的最小深度
- 4.翻转二叉树
- 226.翻转二叉树
- 5.对称二叉树
- 101.对称二叉树
- 572.另一棵树的子树
- 6.二叉树的最大深度
- 104.二叉树的最大深度
- 559.N叉树的最大深度
- 111.二叉树的最小深度
- 7.完全二叉树的节点个数
- 222.完全二叉树的节点个数
- 8.平衡二叉树
- 110.平衡二叉树
- 9.二叉树的所有路径
- 257.二叉树的所有路径
- 10.左叶子之和
- 404.左叶子之和
- 11.找树左下角的值
- 513.找树左下角的值
- 12.路径总和
- 112.路径总和
- 113.路径总和||
- 13.从中序与后序遍历序列构造二叉树
- 106.从中序与后序遍历序列构造二叉树
- 105.从前序与中序遍历序列构造二叉树
- 14.最大二叉树
- 654.最大二叉树
- 15.合并二叉树
- 617.合并二叉树
- 16.二叉搜索树中的搜索
- 700.二叉搜索树中的搜索
- 17.验证二叉搜索树
- 98.验证二叉搜索树
- 18.二叉搜索树的最小绝对差
- 530.二叉搜索树的最小绝对差
- 19.二叉搜索树中的众数
- 501.二叉搜索树中的众数
- 20.二叉树的最近公共祖先
- 236.二叉树的最近公共祖先
- 21.二叉搜索树的最近公共祖先
- 235.二叉搜索树的最近公共祖先
- 22.二叉搜索树中的插入操作
- 701.二叉搜索树中的插入操作
- 23.删除二叉搜索树中的节点
- 450.删除二叉搜索树中的节点
- 24.修剪二叉搜索树
- 669.修剪二叉搜索树
- 25.将有序数组转换为二叉搜索树
- 33.把二叉树转换为累加树
- 538.把二叉搜索树转换为累加树
1.二叉树的递归遍历
144.二叉树的前序遍历
思路:
前序遍历的顺序是,根节点,左孩子,右孩子
终止条件是当前节点为空。
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result=new ArrayList<Integer>();preorder(root,result);return result;}public void preorder(TreeNode root,List<Integer> result) {if(root==null) {return ;}result.add(root.val);preorder(root.left,result);preorder(root.right,result);}
}
145.二叉树的后序遍历
思路:
后续遍历就是最后遍历根节点。递归函数里传入左孩子和右孩子即可。
public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result=new ArrayList<Integer>();postorder(root, result);return result;}public void postorder(TreeNode root,List<Integer> result) {if(root==null) {return ;}postorder(root.left,result);postorder(root.right,result);result.add(root.val);}
94.二叉树的中序遍历

思路:
二叉树的中序遍历就是在中间遍历根节点。
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result=new ArrayList<Integer>();inorder(root, result);return result;}public void inorder(TreeNode root,List<Integer> result) {if(root==null) {return ;}inorder(root.left,result);result.add(root.val);inorder(root.right,result);}
}
2.二叉树的迭代遍历
144.二叉树的前序遍历
思路:
因为递归都是通过栈来实现的,所以我们这里也用栈来实现。
先序遍历的顺序是 中,左,右。
所以我们先让根节点进去,然后操作这个node节点,让它弹出来。然后再让右子节点进去,这样它就会后出来。这样一步步来处理。
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result=new ArrayList<>();Stack<TreeNode> stack=new Stack<>();if(root==null) {return result;}//先在栈中放入根节点stack.push(root);//当栈不为空时while(!stack.isEmpty()) {TreeNode node=stack.pop();result.add(node.val);//先放右节点,因为先进的会压在栈底if(node.right!=null) {stack.push(node.right);}if(node.left!=null) {stack.push(node.left);}}return result;}
145.二叉树的后序遍历

思路:
后续遍历的顺序是,左,右,中
所以可以通过先序遍历的代码,迭代改一下。
因为进栈的顺序是中,左,右,进入result的顺序就是中,右,左,所以再逆转result数组就可以实现左右中。
94.二叉树的中序遍历

思路:
因为加入栈的节点和要处理的节点不一样,所以我们用一个指针来控制。
让指针一直遍历左节点,然后把遍历过的节点加入栈。
当节点是空的时候,栈中弹出元素,并且操作这个元素。让指针指向右节点,看他有没有孩子。
public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result=new ArrayList<>();Stack<TreeNode> stack=new Stack<>();if(root==null) {return result;}TreeNode cur=root;while(cur!=null||!stack.isEmpty()) {if(cur!=null) {//找到最左边的节点,把遍历过的节点加入栈中stack.push(cur);cur=cur.left;}else {cur=stack.pop();result.add(cur.val);cur=cur.right;}}return result;}
3.二叉树的层序遍历
102.二叉树的层序遍历
思路:
层序遍历用队列这中数据结构来实现,先将根节点放入队列中,记录此时层数的值。然后弹出一个节点时,把这个节点的左右孩子加入到队列中。层数的元素个数来判断进入每层的节点。
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {Deque<TreeNode > deque=new LinkedList<TreeNode>();List<List<Integer>> result=new ArrayList<List<Integer>>();if(root!=null) {deque.offer(root);}while(!deque.isEmpty()) {List<Integer> index=new ArrayList<Integer>();//用来记录每一层的元素int len=deque.size();//len用来记录每一层的元素个数while(len-->0) {TreeNode node =deque.poll();index.add(node.val);if(node.left!=null) {deque.add(node.left);}if(node.right!=null) {deque.add(node.right);}}result.add(index);}return result;}
}
107.二叉树的层序遍历||
思路:
将正序遍历的结果逆转一下就行。
class Solution {public List<List<Integer>> levelOrderBottom(TreeNode root) {Deque<TreeNode > deque=new LinkedList<TreeNode>();List<List<Integer>> result=new ArrayList<List<Integer>>();if(root!=null) {deque.offer(root);}while(!deque.isEmpty()) {List<Integer> index=new ArrayList<Integer>();//用来记录每一层的元素int len=deque.size();//len用来记录每一层的元素个数while(len-->0) {TreeNode node =deque.poll();index.add(node.val);if(node.left!=null) {deque.add(node.left);}if(node.right!=null) {deque.add(node.right);}}result.add(index);}Collections.reverse(result);return result;}
}
199.二叉树的右视图
思路:
和前边一样一次遍历每个节点,当遍历到最后一个节点时,再把这个节点加入到结果中。
public List<Integer> rightSideView(TreeNode root) {Deque<TreeNode > deque=new LinkedList<TreeNode>();List<Integer> result=new ArrayList<Integer>();if(root!=null) {deque.offer(root);}while(!deque.isEmpty()) {int len=deque.size();//len用来记录每一层的元素个数while(len-->0) {TreeNode node =deque.poll();if(node.left!=null) {deque.add(node.left);}if(node.right!=null) {deque.add(node.right);}if(len==1) {result.add(node.val);}}}return result;}
637.二叉树的层平均值
思路:
将每层二叉树的和除以每层二叉树的元素个数即可。
class Solution {public List<Double> averageOfLevels(TreeNode root) {Deque<TreeNode > deque=new LinkedList<TreeNode>();List<Double> result=new ArrayList<Double>();if(root!=null) {deque.offer(root);}while(!deque.isEmpty()) {List<Integer> index=new ArrayList<Integer>();//用来记录每一层的元素Double sum=0.0;int len=deque.size();//len用来记录每一层的元素个数int levelsize=deque.size();while(len-->0) {TreeNode node =deque.poll();index.add(node.val);if(node.left!=null) {deque.add(node.left);}if(node.right!=null) {deque.add(node.right);}index.add(node.val);sum+=node.val;}result.add(sum/levelsize);}return result;}
}
429.N叉树的层序遍历
思路:
把以前的左右孩子节点换成一个数组来遍历,当遇到空节点时就算停止。
public List<List<Integer>> levelOrder(Node root) {Deque<Node > deque=new LinkedList<Node>();List<List<Integer>> result=new ArrayList<List<Integer>>();if(root!=null) {deque.offer(root);}while(!deque.isEmpty()) {List<Integer> index=new ArrayList<Integer>();//用来记录每一层的元素int len=deque.size();//len用来记录每一层的元素个数while(len-->0) {Node node =deque.poll();index.add(node.val);List<Node> childern=node.children;for(Node node1:childern) {if(node1!=null) {deque.add(node1);}}}result.add(index);}return result;}
515.在每个树行中找最大值
思路:
注意此时的max值要用Integer.MIN_VALUE来设置,因为可能出现比0小的情况。
public List<Integer> largestValues(TreeNode root) {Deque<TreeNode > deque=new LinkedList<TreeNode>();List<Integer> result=new ArrayList<Integer>();if(root!=null) {deque.offer(root);}while(!deque.isEmpty()) {int len=deque.size();//len用来记录每一层的元素个数int max=Integer.MIN_VALUE;while(len-->0) {TreeNode node =deque.poll();max=node.val>max?node.val:max;if(node.left!=null) {deque.add(node.left);}if(node.right!=null) {deque.add(node.right);}}result.add(max);}return result;}
116.填充每个节点的下一个右侧节点指针
思路:
遍历每一层的时候,先保留第一个节点,然后将这个top指针保留住,每次更新下一个节点就行。
public List<List<Integer>> levelOrder(Node root) {Deque<Node > deque=new LinkedList<Node>();List<List<Integer>> result=new ArrayList<List<Integer>>();if(root!=null) {deque.offer(root);}while(!deque.isEmpty()) {List<Integer> index=new ArrayList<Integer>();//用来记录每一层的元素int len=deque.size();//len用来记录每一层的元素个数while(len-->0) {Node node =deque.poll();index.add(node.val);List<Node> childern=node.children;for(Node node1:childern) {if(node1!=null) {deque.add(node1);}}}result.add(index);}return result;}
117.填充每个节点的下一个右侧节点指针||
思路:
和上边没有任何差别,思路一样。
public Node connect(Node root) {Deque<Node > deque=new LinkedList<Node>();List<Integer> result=new ArrayList<Integer>();if(root!=null) {deque.offer(root);}while(!deque.isEmpty()) {int len=deque.size();//len用来记录每一层的元素个数Node top=deque.pop();//将每层的头节点记录下来if(top.left!=null) {deque.add(top.left);}if(top.right!=null) {deque.add(top.right);}while(len-->1) {Node next =deque.poll();if(next.left!=null) {deque.add(next.left);}if(next.right!=null) {deque.add(next.right);}top.next=next;//将top节点指向下一个节点top=next;//自己变成top节点}}return root;}
104.二叉树的最大深度
思路:每层遍历了多少个就是一共有几层。
public int maxDepth(TreeNode root) {Deque<TreeNode > deque=new LinkedList<TreeNode>();List<Integer> result=new ArrayList<Integer>();if(root!=null) {deque.offer(root);}int dept=0;while(!deque.isEmpty()) {dept++;int len=deque.size();//len用来记录每一层的元素个数int max=Integer.MIN_VALUE;while(len-->0) {TreeNode node =deque.poll();max=node.val>max?node.val:max;if(node.left!=null) {deque.add(node.left);}if(node.right!=null) {deque.add(node.right);}}result.add(max);}return dept;}
111.二叉树的最小深度
思路:
当节点的左右节点都为空时,就代表这个节点为空了。
class Solution {public int minDepth(TreeNode root) {Deque<TreeNode > deque=new LinkedList<TreeNode>();List<Integer> result=new ArrayList<Integer>();if(root!=null) {deque.offer(root);}int dept=0;while(!deque.isEmpty()) {dept++;int len=deque.size();//len用来记录每一层的元素个数while(len-->0) {TreeNode node =deque.poll();if(node.left!=null) {deque.add(node.left);}if(node.right!=null) {deque.add(node.right);}if(node.left==null&&node.right==null) {return dept;}}}return dept;}
}
4.翻转二叉树
226.翻转二叉树
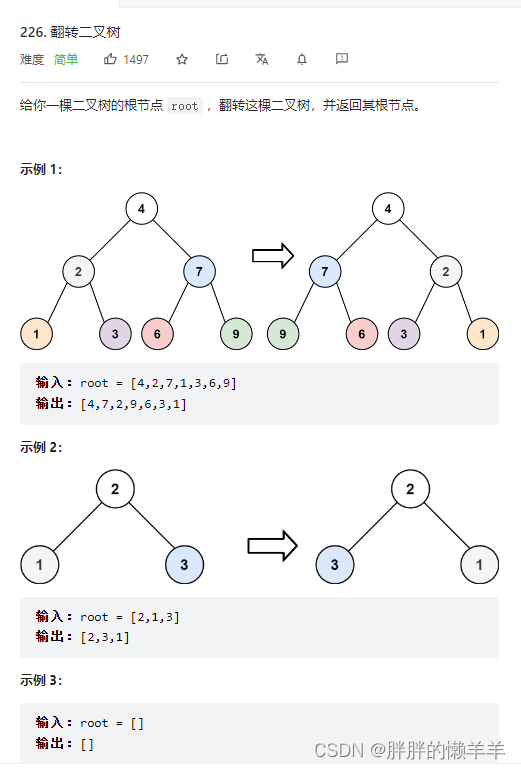
思路:
判断终止条件,结束条件就行,函数体中是翻转两个节点的左右孩子,可以先序遍历,也可以后序遍历。中序遍历则不行。
class Solution {public TreeNode invertTree(TreeNode root) {if(root==null) {return null;}invertTree(root.left);invertTree(root.right);swap(root);return root;}public void swap(TreeNode root) {TreeNode temp=root.left;root.left=root.right;root.right=temp;}}
5.对称二叉树
101.对称二叉树
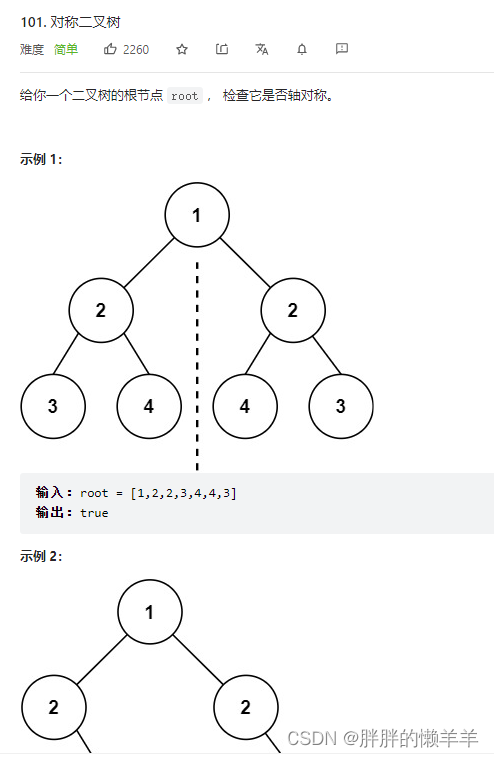
思路:
用递归的方式来进行比较,比较根节点的左右两个子树,判断出终止条件,当两边的值或者有一方为空节点时,都返回false。
运用后序遍历法,先比较外侧节点,再比较内侧节点。最后比较中间节点。
class Solution {public boolean isSymmetric(TreeNode root) {return compare(root.left,root.right);}public boolean compare(TreeNode left,TreeNode right) {if(left==null&&right!=null) {return false;}else if(left!=null&&right==null) {return false;}else if(left==null&&right==null) {return true;}else if(left.val!=right.val) {return false;}boolean outSide=compare(left.left,right.right);boolean inSide=compare(left.right,right.left);return outSide&&inSide;}
}
572.另一棵树的子树
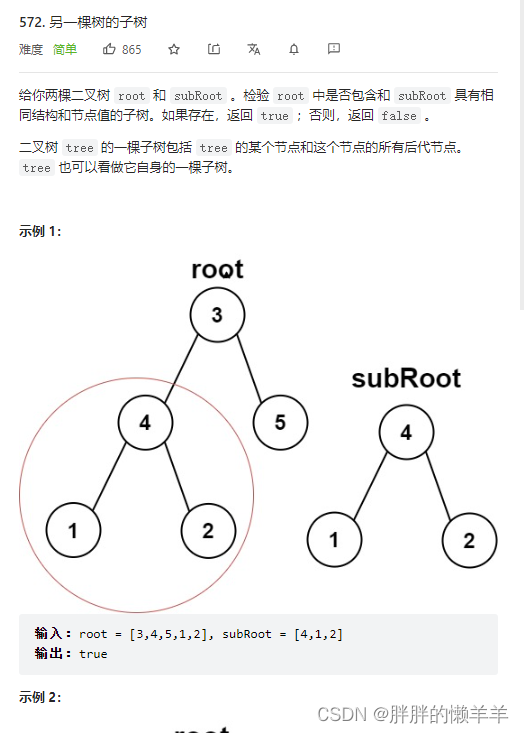
思路:
运用递归法判断,要判断好终止条件,然后写出比较两个子树是否一样的函数。判断,这棵树和比较的树是否一样,或者这颗树的左右子树和比较的树是否一样。这三个条件满足其中一个即可。
class Solution {public boolean compare(TreeNode left,TreeNode right) {if(left==null&&right!=null) {return false;}else if(left!=null&&right==null) {return false;}else if(left==null&&right==null) {return true;}else if(left.val!=right.val) {return false;}boolean outSide=compare(left.left,right.left);boolean inSide=compare(left.right,right.right);return outSide&&inSide;}public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(subRoot==null) {return true;}if(root==null) {return false;}return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot)||compare(root,subRoot);}
}
6.二叉树的最大深度
104.二叉树的最大深度
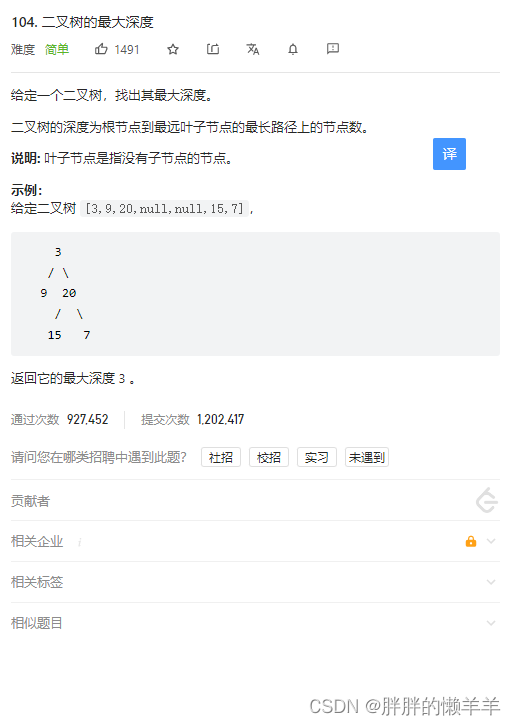
思路:
深度是从根节点往下属。而高度则是从下往上数。
所以,深度是先序遍历,中左右。
高度是后序遍历,左右中。
这里我们求出了根节点的高度,也就求出了二叉树的深度。
public int maxDepth(TreeNode root) {if(root==null) {return 0;}return 1+Math.max(maxDepth(root.left), maxDepth(root.right));}
559.N叉树的最大深度
思路:
递归思路,当遇到空节点时,深度为0。
然后每一次的最大节点就是当前层的孩子的最大节点。
最后return 1+max(children)。
public int maxDepth(Node root) {if(root==null) {return 0;}List<Node> children=root.children;int max=0;for(Node node:children) {max=Math.max(max,maxDepth(node));}return 1+max;}
111.二叉树的最小深度
思路:
这里的最小深度是一个节点的子树的最小深度,如果一个节点还有左节点或者右节点,那么此时它就不能称为一个最小节点。因为它有叶子节点就不能称为一个叶子。所以判断条件上,要分别判断,左子树为空右子树不为空,或左子树不为空,右子树为空,或者左右子树都不为空的情况。
class Solution {public int minDepth(TreeNode root) {if(root==null) {return 0;}int leftDepth=minDepth(root.left);int rightDepth=minDepth(root.right);if(root.left==null&&root.right!=null) {return 1+rightDepth;}if(root.left!=null&&root.right==null) {return 1+leftDepth;}return 1+Math.min(leftDepth, rightDepth);}
}
7.完全二叉树的节点个数
222.完全二叉树的节点个数
思路:
普通解法:运动递归。
class Solution {public int countNodes(TreeNode root) {if(root==null) {return 0;}return countNodes(root.left)+countNodes(root.right)+1;}
}
公式解法:
完全二叉树的满二叉树节点个数是2^n-1。
所以这时候当遇到的节点是满二叉树时,直接用公式求解。
public int countNodes(TreeNode root) {if(root==null) {return 0;}TreeNode left=root.left;TreeNode right=root.right;int leftDept=0;int rightDept=0;while(left!=null) {left=left.left;leftDept++;}while(right!=null) {right=right.right;rightDept++;}if(leftDept==rightDept) {return (2<<leftDept)-1;}return countNodes(root.left)+countNodes(root.right)+1;}
8.平衡二叉树
110.平衡二叉树
思路:
判断左右子树的高度。判断左子树是不是平衡二叉树,如果不是,返回-1.
判断右子树是不是平衡二叉树,如果不是,返回-1.
如果两棵子树的高度差超过1,直接返回-1.
class Solution {public boolean isBalanced(TreeNode root) {if(depth(root)==-1) {return false;}return true;}public int depth(TreeNode root) {if(root==null) {return 0;}//求左子树的高度int leftdepth=depth(root.left);if(leftdepth==-1) {return -1;}int rightdepth=depth(root.right);if(rightdepth==-1) {return -1;}int result;if(Math.abs(leftdepth-rightdepth)>1) {return -1;}else {return 1+Math.max(leftdepth, rightdepth);} }
}
9.二叉树的所有路径
257.二叉树的所有路径
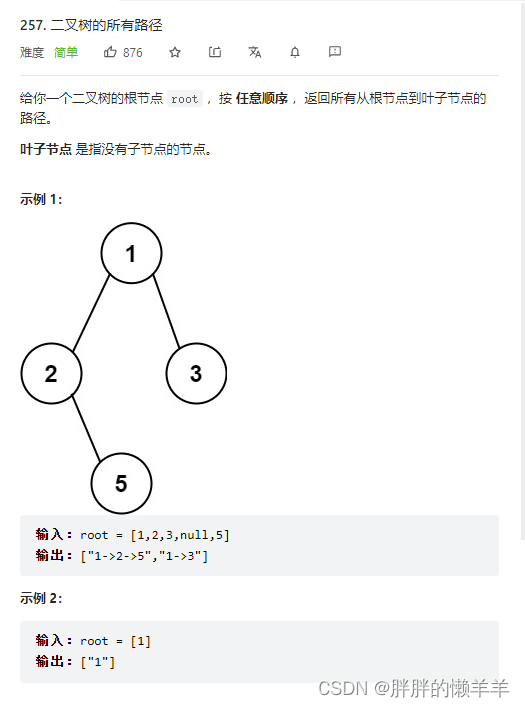
思路:
递归法,先序遍历,中左右。
每次碰到一个节点,把它放入路径中。
如果这个是叶子节点,就可以输入了。
如果不是叶子节点,就继续去递归,递归完之后把最后一个元素弄出来。这就是回溯法。
class Solution {public List<String> binaryTreePaths(TreeNode root) {List<String> result=new ArrayList<String>();if(root==null) {return result;}List<Integer> paths=new ArrayList<Integer>();traversal(root,paths,result);return result;}public void traversal(TreeNode root,List<Integer>paths,List<String> result) {paths.add(root.val);//如果遇到了叶子节点,就要考虑输出了。if(root.left==null&&root.right==null) {StringBuilder path=new StringBuilder();for(int i=0;i<paths.size()-1;i++) {path.append(paths.get(i)).append("->");}path.append(paths.get(paths.size()-1));result.add(path.toString());return ;}//如果左节点不为空if(root.left!=null) {traversal(root.left,paths,result);//进行回溯操作,把最后一个节点弹出去paths.remove(paths.size()-1);}//如果右节点不为空if(root.right!=null) {traversal(root.right,paths,result);paths.remove(paths.size()-1);}}}
10.左叶子之和
404.左叶子之和
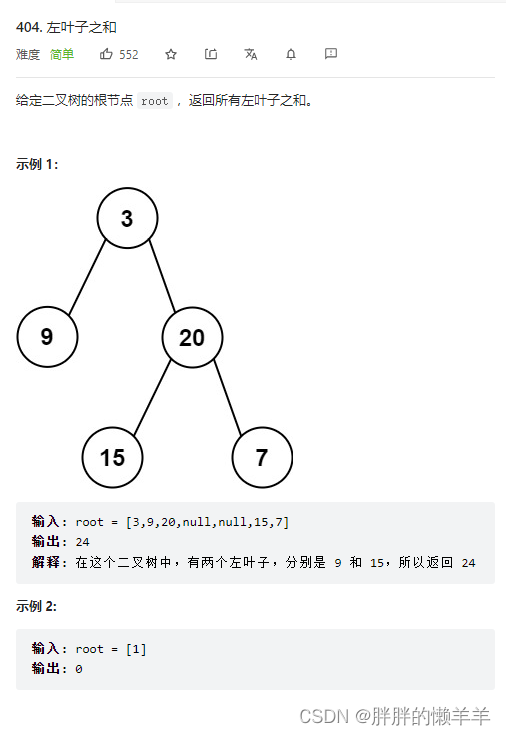
思路:
如果遇到空节点,返回null。
总和是左子树的左节点之和加上右子树的左节点之和。
判断左节点时要从它的父节点找,当父节点有左节点时并且左节点没有左右孩子节点。就可以了。
class Solution {public int sumOfLeftLeaves(TreeNode root) {if(root==null) {return 0;}int leftSum=sumOfLeftLeaves(root.left);int rightSum=sumOfLeftLeaves(root.right);int middle=0;if(root.left!=null&&root.left.left==null&&root.left.right==null) {middle=root.left.val;}return middle+leftSum+rightSum;}
}
11.找树左下角的值
513.找树左下角的值
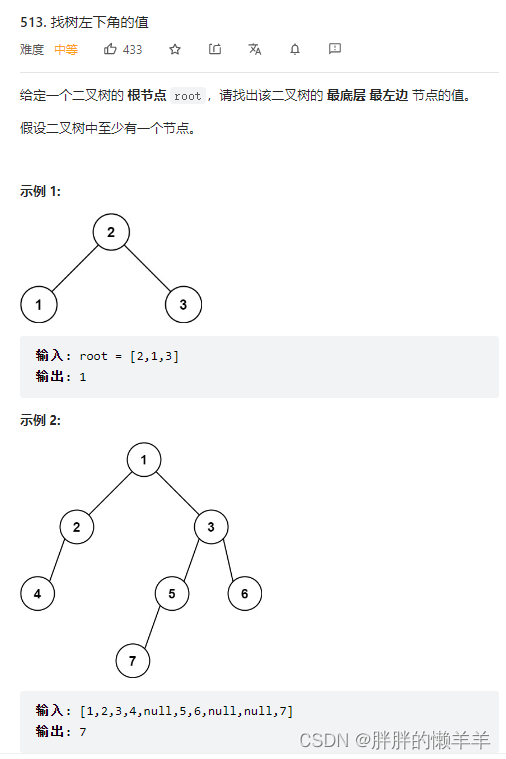
思路:
用迭代法比较简单。
这里使用递归法。用一个额外变量记录最大深度。用额外变量记录result。当找到叶子节点时,判断此时是不是最大深度,如果是,更新value值,因为是先进行左节点遍历,所以会先找到最大层数的左节点。
class Solution {private int Deep = -1;private int value = 0;public int findBottomLeftValue(TreeNode root) {value=root.val;findLeftValue(root,0);return value;}public void findLeftValue(TreeNode root,int dept) {if(root==null) {return ;}//找到叶子节点if(root.left==null&&root.right==null) {if(dept>Deep) {Deep=dept;value=root.val;}}//先找左节点if(root.left!=null) {dept++;findLeftValue(root.left,dept);dept--;//用到了回溯找完左节点再退回去找右节点}if(root.right!=null) {dept++;findLeftValue(root.right,dept);dept--;}}
}
12.路径总和
112.路径总和
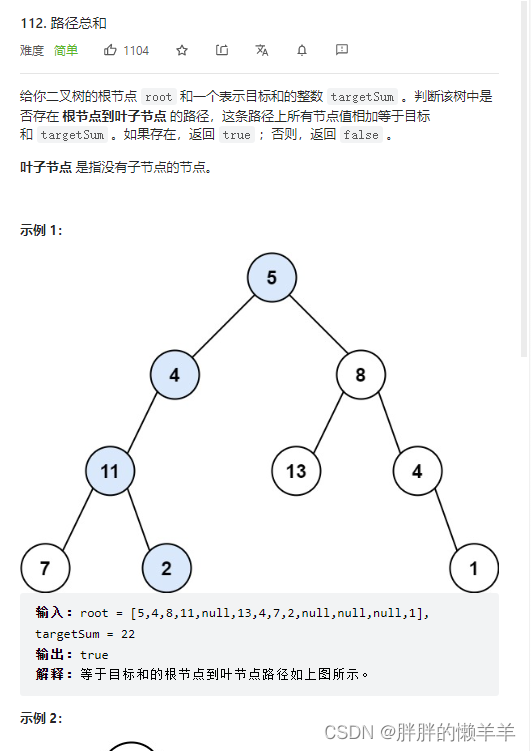
思路:
这道题只是判断有没有对应的路径满足条件,所以不需要做输出处理。
当遍历到一个节点时,需要减去这个节点的值,最后当遍历到叶子节点时,判断数值是不是0即可。
public boolean hasPathSum(TreeNode root, int targetSum) {if(root==null) {return false;}//当弹出去的时候就相当于了回溯的过程targetSum-=root.val;if(root.left==null&&root.right==null) {return targetSum==0;}if(root.left!=null) {boolean left=hasPathSum(root.left,targetSum);//当判断左子树满足条件时,才会直接返回true,所以当是false的时候不会直接终止函数if(left) {return true;}}if(root.right!=null) {boolean right=hasPathSum(root.right,targetSum);if(right) {return true;}}return false;}113.路径总和||
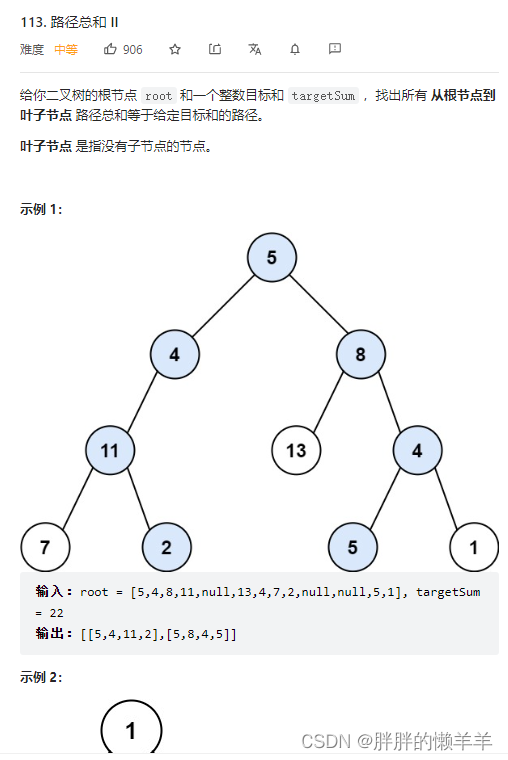
思路:
把所有的路径都遍历一遍,就是不需要返回值,把结果数组放入res里面即可。注意要有回溯操作。
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {List<List<Integer>> res=new ArrayList<>();if(root==null) return res;List<Integer> path=new LinkedList<>();preorderdfs(root,targetSum,res,path);return res;}public void preorderdfs(TreeNode root, int targetsum, List<List<Integer>> res, List<Integer> path) {path.add(root.val);//遇到了叶子节点if(root.left==null&&root.right==null) {//找到了和为targetSum的路径if(targetsum-root.val==0) {res.add(new ArrayList<>(path));}return ;}if(root.left!=null) {preorderdfs(root.left, targetsum-root.val, res, path);//回溯path.remove(path.size()-1);}if(root.right!=null) {preorderdfs(root.right,targetsum-root.val,res,path);path.remove(path.size()-1);}}
13.从中序与后序遍历序列构造二叉树
106.从中序与后序遍历序列构造二叉树
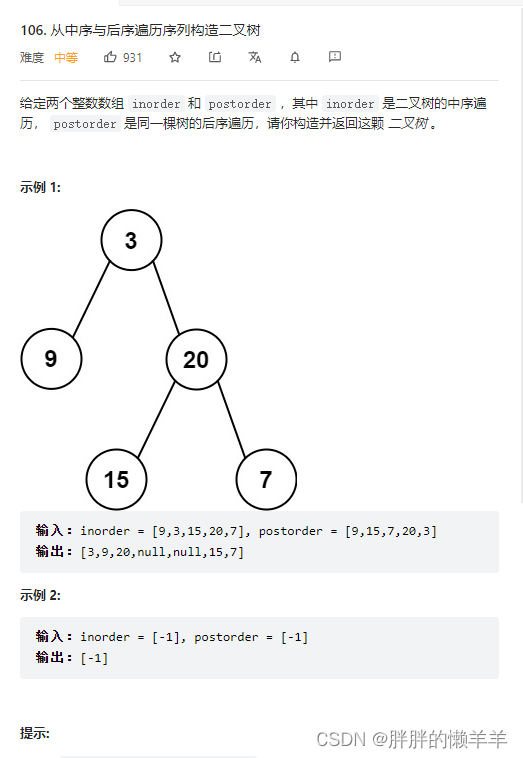
思路:
1.找到后序遍历的最后一个节点就是根节点。
2.根据根节点去切割中序遍历,可以找到左子树和右子树的范围。
3.根据中序遍历中左子树和右子树的范围,可以找到后序遍历中的左子树和右子树。
4.然后再进行递归求解,中序遍历的左子树和后序遍历的左子树这又是一个新的条件。所以可以继续求解。
Map<Integer,Integer> map;public TreeNode buildTree(int[] inorder, int[] postorder) {map=new HashMap<>();for(int i=0;i<inorder.length;i++) {//用map保存中序序列的数值对应位置map.put(inorder[i], i);}return findNode(inorder,0,inorder.length,postorder,0,postorder.length);}public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {if(inBegin>=inEnd||postBegin>=postEnd) {return null;}//找到中序遍历中根节点的位置int rootIndex=map.get(postorder[postEnd-1]);TreeNode root=new TreeNode(inorder[rootIndex]);//根据根节点的位置确定中序遍历总左子树的数量int lengthofLeft=rootIndex-inBegin;root.left=findNode(inorder,inBegin,rootIndex,postorder,postBegin,postBegin+lengthofLeft);//左子树分别在中序和后序的位置root.right=findNode(inorder,rootIndex+1,inEnd,postorder,postBegin+lengthofLeft,postEnd-1);//右子树分别在中序和后序的位置return root;}
105.从前序与中序遍历序列构造二叉树
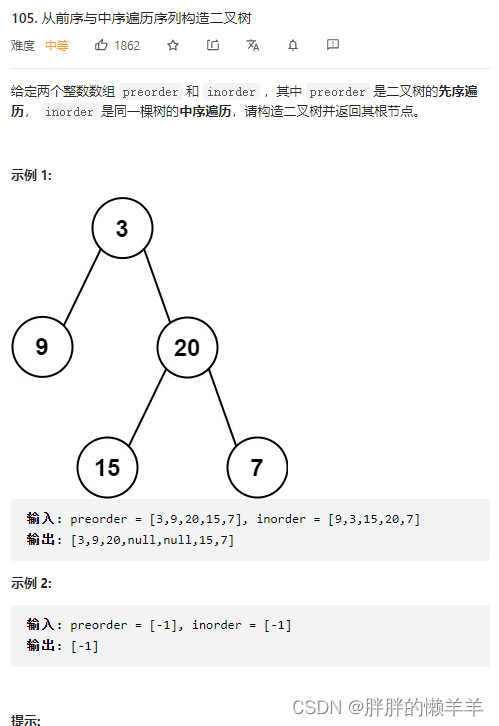
思路:
和后序中序生成二叉树一样。
依靠先序第一个节点找到根节点。然后再根据根节点在中序上找,找到位置就可以分出左子树和右子树。
这样两种遍历方式的左右子树都分出来了。最后就递归生成即可。
Map<Integer,Integer>map;public TreeNode buildTree(int[] preorder, int[] inorder) {map=new HashMap<>();//把中序遍历中每个元素出现的位置存起来for(int i=0;i<inorder.length;i++) {map.put(inorder[i],i);}return findNode(preorder,0,preorder.length,inorder,0,inorder.length);}public TreeNode findNode(int[] preorder,int preBegin,int preEnd,int[] inorder, int inBegin, int inEnd) {//参数范围都是前闭后开if(preBegin>=preEnd||inBegin>=inEnd) {return null;}int rootIndex=map.get(preorder[preBegin]);//找到根节点在中序遍历的位置TreeNode root=new TreeNode(inorder[rootIndex]);//找到左子树的数量int lengthOfLeft=rootIndex-inBegin;root.left=findNode(preorder,preBegin+1,preBegin+1+lengthOfLeft,inorder,inBegin,inBegin+lengthOfLeft);root.right=findNode(preorder,preBegin+1+lengthOfLeft,preEnd,inorder,rootIndex+1,inEnd);return root;}
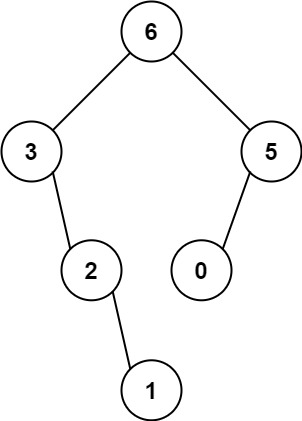
14.最大二叉树
654.最大二叉树
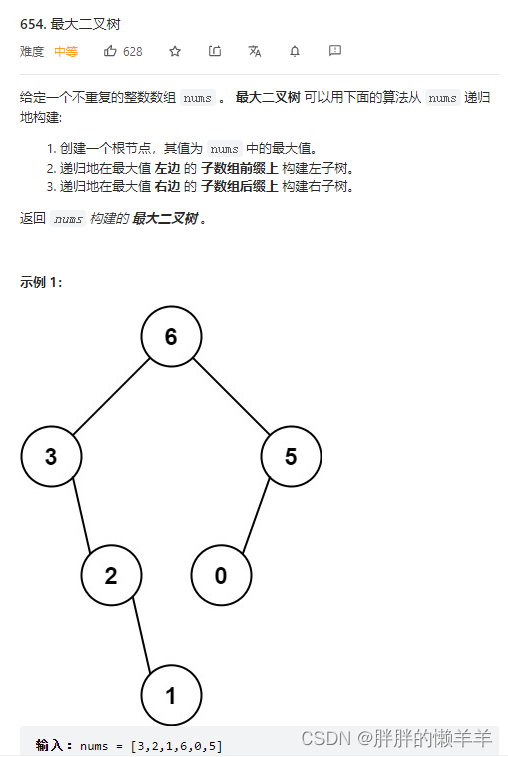
思路:
递归函数里要确定终止条件。
1.当区间里没有元素时,直接返回null。
2.当区间里只有一个元素时,直接构造一个节点。
3.找到这个区间里的最大值和最大元素下标。
4.用最大值创建一个节点。根据最大元素下标去切分剩下的数组。来生成左子树和右子树。
public TreeNode constructMaximumBinaryTree(int[] nums) {return constructMaximumBinaryTree1(nums,0,nums.length);}public TreeNode constructMaximumBinaryTree1(int[] nums,int leftIndex,int rightIndex) {//判断终止条件,如果区间里边没有元素了直接返回if(leftIndex>=rightIndex) {return null;}//如果区间里边只有一个元素,那么直接返回这个节点if((rightIndex-leftIndex)==1) {return new TreeNode(nums[leftIndex]);}//找到区间里最大的元素和下标。找最大的元素构造根节点,找到下标用来切分数组int maxValue=nums[leftIndex];int maxIndex=leftIndex;for(int i=leftIndex+1;i<rightIndex;i++) {if(nums[i]>maxValue) {maxValue=nums[i];maxIndex=i;}}//用这个最大的元素来构造根节点TreeNode root=new TreeNode(maxValue);//递归去找左子树root.left=constructMaximumBinaryTree1(nums,leftIndex,maxIndex);root.right=constructMaximumBinaryTree1(nums,maxIndex+1,rightIndex);return root;}15.合并二叉树
617.合并二叉树

思路:
用递归来做,当左子树是空时,返回右子树。
当右子树是空时,返回左子树。
然后合并之后的树等于左子树和右子树两个数的继续合并。
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if(root1==null) {return root2;}if(root2==null) {return root1;}root1.val+=root2.val;root1.left=mergeTrees(root1.left,root2.left);root1.right=mergeTrees(root1.right,root2.right);return root1;}
16.二叉搜索树中的搜索
700.二叉搜索树中的搜索
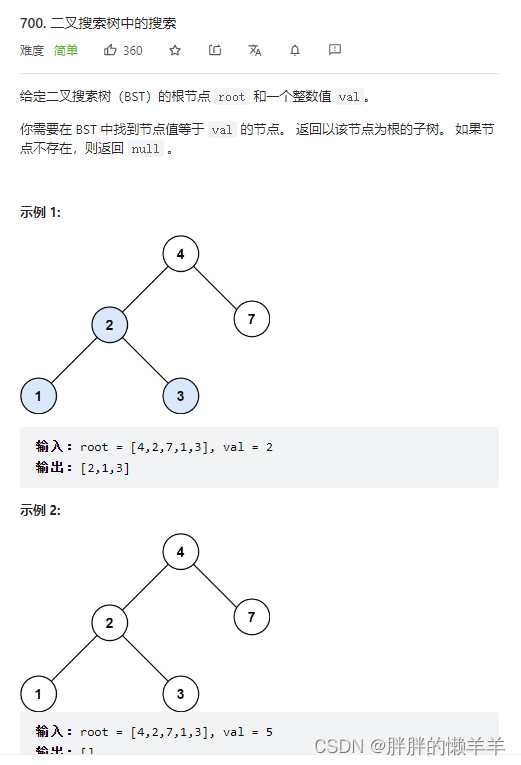
思路:
终止条件:当遇到的节点是空时,或者遇到的节点的值等于目标值时,返回这个节点。
根据二叉搜索树的特点,
递归里的逻辑:当节点的值比目标值小时,向右子树查找。当节点的值比目标值大时,向左子树查找。
public TreeNode searchBST(TreeNode root, int val) {//终止条件if(root==null||root.val==val) {return root;}//递归里的逻辑TreeNode node=null;if(root.val>val) {node=searchBST(root.left,val);}else if(root.val<val) {node=searchBST(root.right,val);}return node;}17.验证二叉搜索树
98.验证二叉搜索树
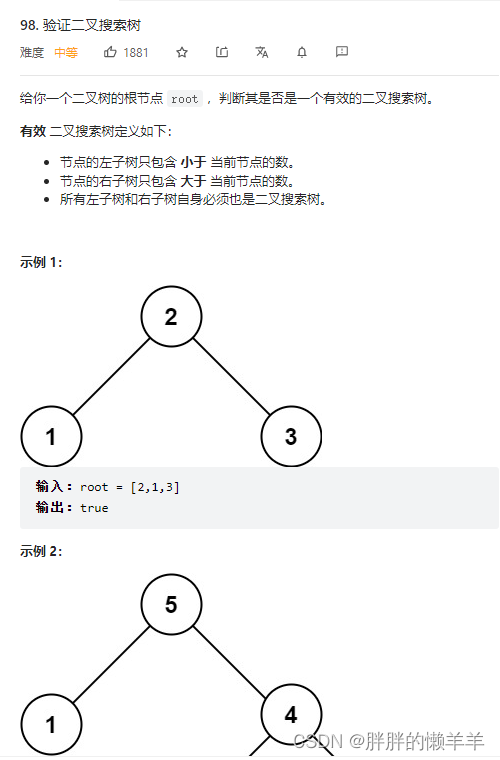
思路:
用一个指针去记录左边的节点,当这个节点不等于null并且数值大于等于中间的节点的时候,就判断出了它不是二叉搜索树。返回false。
public TreeNode pre;public boolean isValidBST(TreeNode root) {//当节点为空的时候if(root==null) {return true;}//判断左边是不是二叉搜索树boolean left=isValidBST(root.left);if(!left) {return false; }//判断中间是不是二叉搜索树if(pre!=null&&pre.val>=root.val) {return false;}pre=root;boolean right=isValidBST(root.right);return left&&right;}
18.二叉搜索树的最小绝对差
530.二叉搜索树的最小绝对差
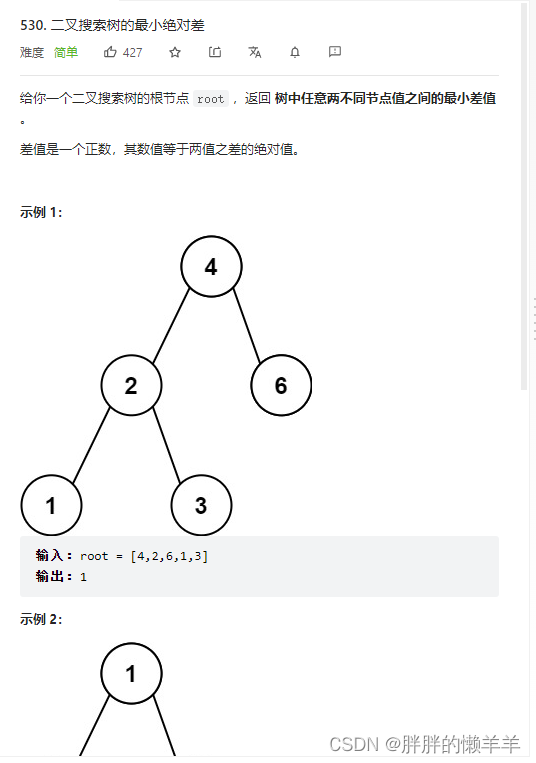
思路:
定义两个指针,一个前指针,一个后指针,两个指针一步一步的走,采用中序遍历的方式,如果一步一步的走,将每次最小的差值记录下来。
class Solution {public int result=Integer.MAX_VALUE;TreeNode pre1;public int getMinimumDifference(TreeNode root) {if(root==null) return 0;traversal(root);return result;}public void traversal(TreeNode root) {if(root==null) {return ;}//采用中序遍历traversal(root.left);if(pre1!=null) {result=(root.val-pre1.val)<result?(root.val-pre1.val):result;}pre1=root;traversal(root.right);}
}
19.二叉搜索树中的众数
501.二叉搜索树中的众数

思路:
有一个maxcount变量来记录出现最大的次数。count记录当前数字出现的数。如果前指针和后指针不相等时,count等于1,代表出现一次。然后每次相等的时候count++。
当count=maxcount的时候,把结果更新进去,如果count大于maxcount了只需要清空结果集里的元素然后把后面的元素加进去即可。
List<Integer> res=new ArrayList<Integer>();int maxCount=0;int count=0;TreeNode pre2=null;public int[] findMode(TreeNode root) {if(root==null) {return res.stream().mapToInt(x->x).toArray() ;}findMode(root.left);if(pre==null||root.val!=pre.val) {count=1;}else {count++;}//更新结果以及maxCountif(count>maxCount) {res.clear();res.add(root.val);maxCount=count;}else if(count==maxCount) {res.add(root.val);}pre=root;findMode(root.right);return res.stream().mapToInt(x->x).toArray() ;}
20.二叉树的最近公共祖先
236.二叉树的最近公共祖先
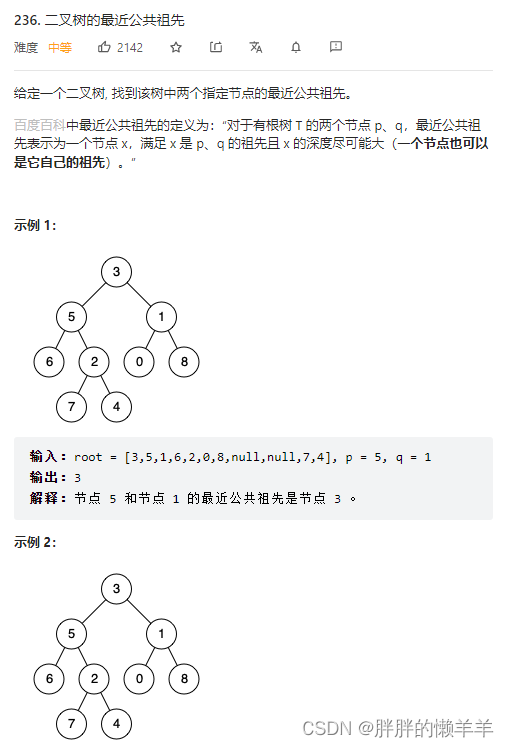
思路:
终止条件:当节点为空时或者左节点找到了目标节点,或者右节点找到了目标节点。
采用后序遍历的方法。
先看左子树有没有目标值,再看右子树有没有目标值。
如果左子树和右子树都有了目标值,直接返回root。
如果两个子树中仅有一个有目标值,返回这个子树即可。
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root==null||root==p||root==q) {//递归条件结束,当有一个节点找到p或q时,递归结束return root;}//采用后序遍历TreeNode left=lowestCommonAncestor(root.left,p,q);TreeNode right=lowestCommonAncestor(root.right,p,q);//当两个节点都没找到时if(left==null&&right==null) {return null;}else if(left==null&&right!=null) {//当右节点找到一个目标值时,左节点没有找到,返回右节点return right;}else if(left!=null&&right==null) {//当左节点找到一个目标值时,右节点没有找到,返回左节点return left;}else {return root;//当两个节点都找到了目标值,直接返回root}}
21.二叉搜索树的最近公共祖先
235.二叉搜索树的最近公共祖先
思路:
当根节点为空时返回null。
当根节点的数值大于目标节点的数值时。往左子树查找,如果左子树不为空,直接返回左子树即可。
当根节点的数值小于目标节点的数值时。往右子树查找,如果右子树不为空,直接返回右子树即可。
如果根节点的数值在两个节点之间。那么返回这个节点即可。
public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) {//二叉搜索树因为知道了节点大小,所以搜索起来会方便很多。if(root==null) {return null;}if(root.val>p.val&&root.val>q.val) {//说明根节点的数值比两个目标值大,所以结果在左边TreeNode left=lowestCommonAncestor2(root.left,p,q);if(left!=null) {//如果左节点不等于null,直接返回即可return left;}}if(root.val<p.val&&root.val<q.val) {//说明根节点的数值比两个目标值小,所以结果在右边TreeNode right=lowestCommonAncestor2(root.right,p,q);if(right!=null) {//如果右节点不等于null,直接返回即可。return right;}}return root;}
22.二叉搜索树中的插入操作
701.二叉搜索树中的插入操作
思路:用递归法,当遇到空节点时,直接生成节点,然后返回这个节点。这样递归函数返回到上一层时,让左子树的节点指向这个节点。
public TreeNode insertIntoBST(TreeNode root, int val) {//当遇到的节点为空时,构造新的节点if(root==null) {TreeNode children=new TreeNode(val);return children;}//如果节点的值比目标值大,往左子树去插if(root.val>val) {root.left=insertIntoBST(root.left,val);}//如果节点的值比目标值小,往右子树去插if(root.val<val) {root.right=insertIntoBST(root.right,val);}return root;}
23.删除二叉搜索树中的节点
450.删除二叉搜索树中的节点
思路:
把5种情况理清楚就可以了。
public TreeNode deleteNode(TreeNode root, int key) {/*** 分为五种情况,key没有找到* 删除叶子节点* 删除节点有左子树,直接让它指向左子树即可* 删除节点有右子树,直接让它指向右子树即可* 删除节点左右子树都有,找到右子树的最小节点的值,然后让这个子树的左节点指向它即可。*/if(root==null) {return null;}if(root.val==key) {//找到了节点if(root.left==null&&root.right==null) {//删除叶子节点return null;}else if(root.left!=null&&root.right==null) {//删除节点有左子树return root.left;}else if(root.left==null&&root.right!=null) {//删除节点有右子树return root.right;}else {TreeNode cur=root.right;//找到右子树的最左边的节点while(cur.left!=null) {cur=cur.left;}cur.left=root.left;return root.right;}}//告诉节点规则,让它在哪个方向去找Keyif(root.val>key) {root.left=deleteNode(root.left,key);}else if(root.val<key) {root.right=deleteNode(root.right,key);}return root;}
24.修剪二叉搜索树
669.修剪二叉搜索树
思路:
当修剪到叶子节点时,节点比左边界要小,返回这个节点修剪后的右子树给上一个节点。节点比右边界要大,返回这个节点修剪后的左子树给上一个节点。如果这个节点恰好在两个中间,那么直接返回这个节点即可。
public TreeNode trimBST(TreeNode root, int low, int high) {//当遇到空节点,返回nullif(root==null) {return null;}//当遇见的节点比左边界的值要小,让右子树去剪枝,返回右子树if(root.val<low) {TreeNode right=trimBST(root.right,low,high);return right;}//当遇见的节点比右边界的值要大,让左子树去剪枝,返回左子树if(root.val>high) {TreeNode left=trimBST(root.left,low,high);return left;}//当遇见的节点在两个边界点之间。分别对左右两个子树减枝即可root.left=trimBST(root.left,low,high);root.right=trimBST(root.right,low,high);return root;}
25.将有序数组转换为二叉搜索树
思路:
用递归的方式,找到中间节点,然后生成这个节点,递归去遍历左右区间。
public TreeNode sortedArrayToBST(int[] nums) {return sortedArray(nums,0,nums.length-1);}public TreeNode sortedArray(int[]nums,int left,int right) {//运用中节点,递归去处理,采用左闭右闭区间if(left>right) {return null;}int mid=(left+right)/2;TreeNode root=new TreeNode(nums[mid]);root.left=sortedArray(nums,left,mid-1);root.right=sortedArray(nums,mid+1,right);return root;}
33.把二叉树转换为累加树
538.把二叉搜索树转换为累加树
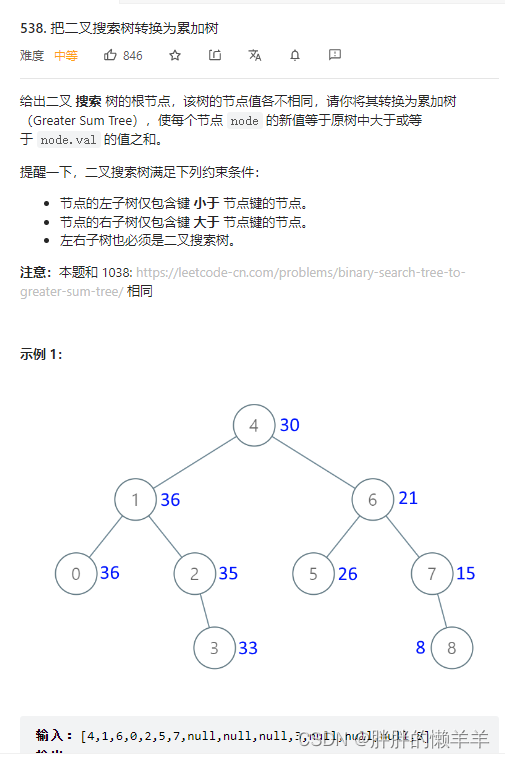
思路:
用右中左的顺序去遍历,把前一个节点的值记录好,然后顺序更新即可。
int pre3=0;public TreeNode convertBST(TreeNode root) {//右中左的顺序去遍历,然后每次更新pre的树枝即可.if(root==null) {return null;}convertBST(root.right);//中间节点的逻辑root.val+=pre3;pre3=root.val;convertBST(root.left);return root;}
相关文章:

LeetCode分类刷题----二叉树
二叉树1.二叉树的递归遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历2.二叉树的迭代遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历3.二叉树的层序遍历102.二叉树的层序遍历107.二叉树的层序遍历||199.二叉树的右视图637.二叉树的层平均…...
)
Zipkin : Golang 微服务全链路监控(三)
Zipkin : Golang 微服务全链路监控(三) Golang 微服务全链路监控实现 broker-service -> auth-service -> postgres dbzipkin 监控:需代码入侵 使用 zipkin 库的 serverMiddleware,其通过 Http 跟踪(trace&am…...
5.3 BGP路由黑洞
5.2.3实验3:BGP路由黑洞 1. 实验目的 熟悉BGP路由黑洞的应用场景掌握BGP水平分割的配置方法2. 实验拓扑 实验拓扑如图5-3所示: 图5-3:BGP路由黑洞 3. 实验步骤 配置IP地址 R1的配置 <Huawei>syst...
STM32 DFU模式烧录代码
什么是DFU? dfu的本质是isp,usb接口的isp,在系统编程,进入isp的方式我们先了解 如下图 boot0为高电平 boot1为低电平即可进入isp模式。 熟悉的场景 在我们使用flymcu软件下载代码时,本质也是isp 串口接口的isp。 傻瓜使用方式…...
松下PLC通过fpwin上传写入MRTC模块方法
目录 PLC程序上传方法 加密模块使用 PLC程序上传方法 手动将PLC模式设置为prog模式查看PLC是否设置为禁止上传查询指示灯是否变蓝,变蓝则需要将PLC禁止上传功能取消。 3.当上述动作操作完成后,将PLC程序导入到PLC中。为了配合加密程序使用,…...

就业大山之下的网络安全:安逸的安服仔
从去年开始,各个互联网大厂就接二连三的放出了裁员消息,整个互联网行业好像都处于寒冬状态。微博、小米、滴滴、知乎、拼多多等在内的一大批互联网知名企业,也相继传出“人员优化”的消息。 除了国内市场的萧条,国外市场也是不容…...
JavaWeb3-线程的3种创建方式7种写法
目录 1.方式一:继承Thread(2种写法) 写法①(常规): a.使用jconsole观察线程 b.启动线程——start方法 PS:(常见面试题)start 方法与 run 方法的区别: 写…...

驱动调试手段
文章目录 前言一、通过sysfs调试LCD查看电源:查看 pwm 信息查看管脚信息总结前言 本文记录在驱动中常用的调试手段 提示:以下是本篇文章正文内容,下面案例可供参考 一、通过sysfs 系统起来之后可以读取 sysfs 一些信息,来协助调试 示例: 调试LCD 输入如下命令 cat /…...

[RK3568 Android12] 音频及路由
1:概述(耳机 ,hdmiin ,板载喇叭) 在开发板上面,系统注册了三个音频输出通道,如下: [ 2.280612] ALSA device list: [ 2.280622] #0: rockchip,rk809-codec [ 2.280630] #1: ROCKCHIP,SPDIF [ 2.280638] #2: rockchip,hdmi console:/proc/asound # cat pcm …...

C++——C++11 第一篇
目录 统一的列表初始化 {}初始化 decltype 编辑 nullptr STL中一些变化 右值引用和移动语义 左值引用和右值引用 总结 左值引用优缺点 右值引用(将亡值) 拷贝赋值和移动赋值 万能引用|完美转发 移动构造和移动赋值注意…...
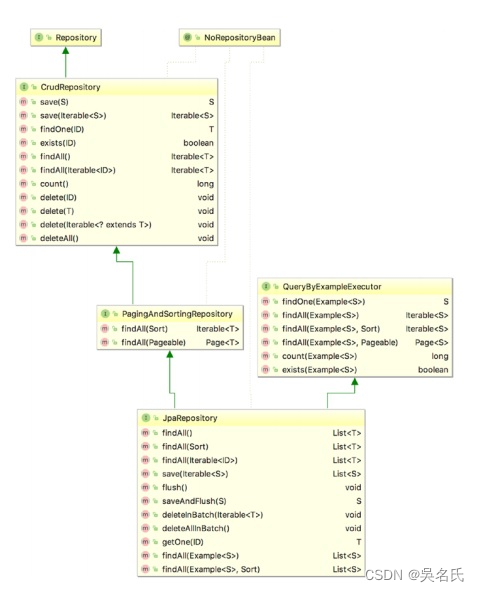
Spring Data JPA 中 CrudRepository 和 JpaRepository 的区别
1 问题描述Spring Data JPA 中,CrudRepository 和 JpaRepository 有何区别?当我在网上找例子的时候,发现它们可以互相替换使用。它们有什么不同呢?为什么你习惯用其中的一个而不是另一个呢?2 CrudRepository 和 JpaRep…...

推荐几款好用的数据库管理工具
本文主要介绍几款常用的数据库管理软件(客户端),包括开源/免费的、商用收费的,其中有一些是专用于 MySQL 数据库的,例如 MySQL Workbench、phpMyAdmin,有一些是支持多种 SQL、NoSQL 数据库的,例…...

DPDK — 性能优化手段
目录 文章目录 目录硬件布局层面的优化操作系统层面的优化Linux 操作系统版本应用程序层面的优化Cache 优化内存对齐内存预取SIMD 报文批处理DDIO使用高级 CPU 指令集硬件布局层面的优化 DPDK 在硬件布局层面的优化,主要体现在以下几个方面: CPU 频率的高低:CPU 频率越高,…...

Fedora Linux未来五年规划
Fedora 委员会一直致力于起草战略计划,以帮助 Fedora Linux 更好地发展。近日 Fedora 委员会公布了一份 “《未来五年的 Fedora Linux 》” 战略计划草案,这份草案里面包含了他们的雄心壮志:每周将 Fedora 的活跃贡献者人数增加一倍。 Fedora…...
【C++之容器篇】map和set常见函数接口的使用与剖析
目录前言一、set1. 简介2. 成员类型3. 构造函数(1) set()(2)set(InputIterator first,InputIterator last)(3)使用4. 拷贝构造函数和赋值运算符重载5. empty()6. size()7. insert()(1)pair<iterator,bool> insert(const K& key)(2)iterator insert(iterator pos,cons…...
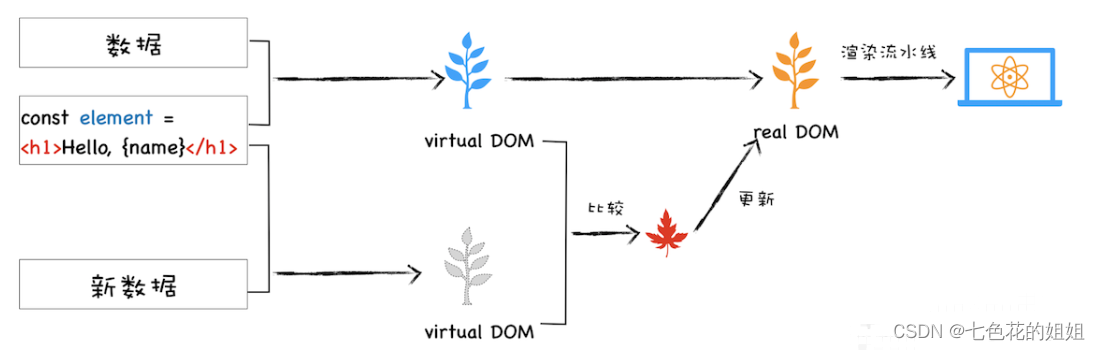
虚拟DOM是什么
参考文章做的总结,如有不足之处请指正! 在讲虚拟dom之前,先讲讲,为什么前端操作dom会导致页面性能降低? 先说几个概念 有助于后面的理解 什么是 JavaScript 引擎? JavaScript引擎是一个专门处理JavaScript脚…...
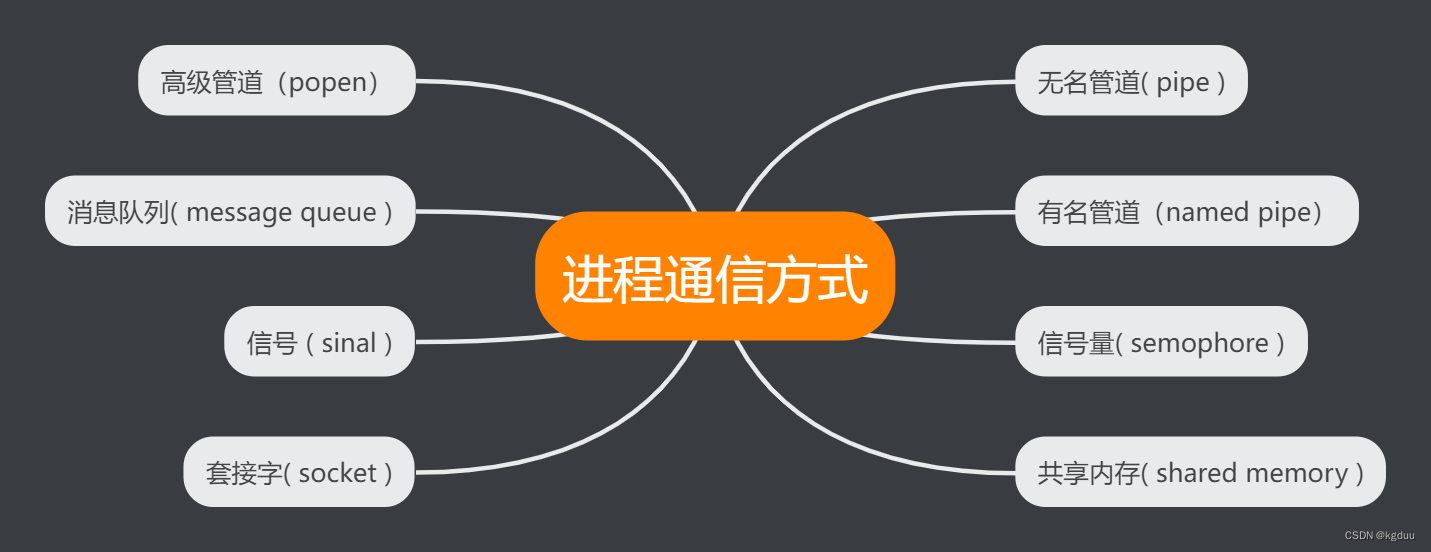
进程通信方式
无名管道( pipe ): 管道是一种半双工的通信方式,数据只能单向流动,而且只能在具有亲缘关系的进程间使用。进程的亲缘关系通常是指父子进程关系。高级管道(popen): 将另一个程序当做一个新的进程在当前程序进…...
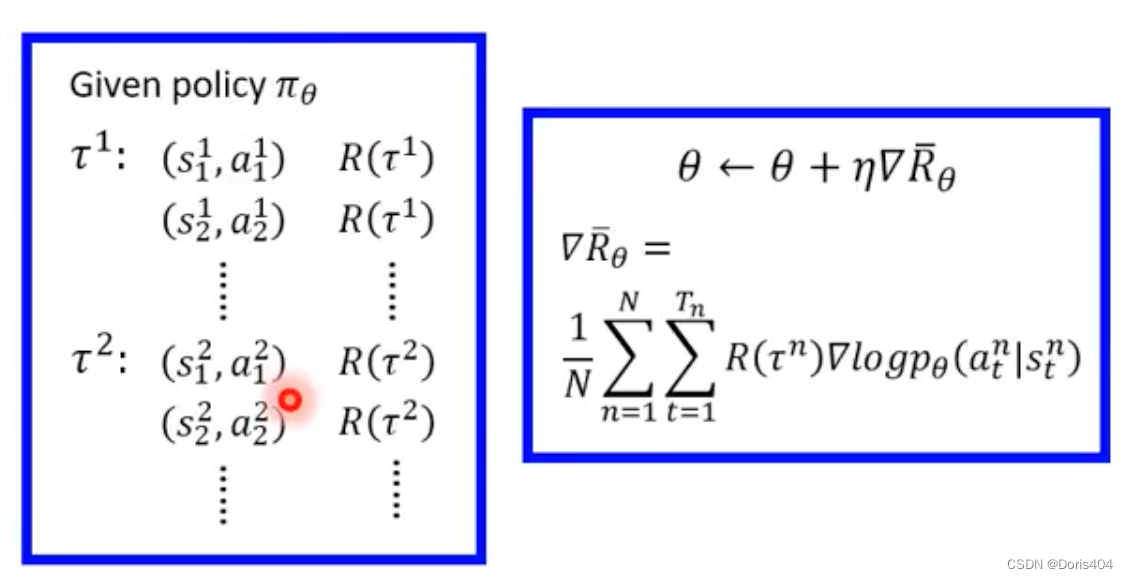
强化学习基础知识
强化学习是一种机器学习方法,通过agent与environment的互动,学习适当的action policy以取得更大的奖励reward。本篇博客介绍强化学习的基础知识,与两类强化学习模型。 目录强化学习的基础设定policy based 强化学习的目标3个注意事项实际训练…...
LeetCode230218_148、654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 nums 构建的 最大二叉树…...

WordPress 是什么?.com 和 .org 的 WordPress 有什么差异?
本篇文章会介绍这次WordPress 5.8核心版本所带来的其中一项新功能:内存块小工具(Widget)此次更新把小工具编辑设定的页面也改成用「内存块编辑」的概念,就跟内置的「古腾堡」编辑器一样,把所有元件都内存块化ÿ…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
