The 22nd Japanese Olympiad in Informatics (JOI 2022/2023) Final Round 题解
交题:https://cms.ioi-jp.org/documentation
A
给一个序列 a1,⋯,ana_1,\cdots,a_na1,⋯,an。
执行nnn个操作,第iii个操作为找出第iii个数前离其最近且与它相同的数的位置,把这两个数之间的数全部赋值aia_iai。求最后的序列。
考虑第iii个操作执行完后,iii之前每个数一定是连续出现正好一段或不出现。
#include<bits/stdc++.h>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define ForkD(i,k,n) for(int i=n;i>=k;i--)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=next[p])
#define Lson (o<<1)
#define Rson ((o<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,0x3f,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define MEMx(a,b) memset(a,b,sizeof(a));
#define INF (0x3f3f3f3f)
#define F (1000000007)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define vi vector<int>
#define pi pair<int,int>
#define SI(a) ((a).size())
#define Pr(kcase,ans) printf("Case #%d: %lld\n",kcase,ans);
#define PRi(a,n) For(i,n-1) cout<<a[i]<<' '; cout<<a[n]<<endl;
#define PRi2D(a,n,m) For(i,n) { \For(j,m-1) cout<<a[i][j]<<' ';\cout<<a[i][m]<<endl; \}
#pragma comment(linker, "/STACK:102400000,102400000")
#define ALL(x) (x).begin(),(x).end()
#define gmax(a,b) a=max(a,b);
#define gmin(a,b) a=min(a,b);
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
ll mul(ll a,ll b){return (a*b)%F;}
ll add(ll a,ll b){return (a+b)%F;}
ll sub(ll a,ll b){return ((a-b)%F+F)%F;}
void upd(ll &a,ll b){a=(a%F+b%F)%F;}
inline int read()
{int x=0,f=1; char ch=getchar();while(!isdigit(ch)) {if (ch=='-') f=-1; ch=getchar();}while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar();}return x*f;
}
int a[201000];
map<int,pair<int,int> > h;
int main()
{
// freopen("A.in","r",stdin);
// freopen(".out","w",stdout);int n=read();For(i,n) a[i]=read(); stack <pair<pair<int,int> , int > > st;For(i,n) {if(st.empty() || !h.count(a[i]) || h[a[i]] ==mp(0,0) ) {st.push(mp(mp(i,i),a[i]));h[a[i]]=mp(i,i);}else {while(!st.empty()) {auto p=st.top();st.pop();if(p.se==a[i]) {h[p.se]=mp(p.fi.fi,i);st.push(mp(h[p.se],a[i]));break;}else {h[p.se]=mp(0,0);}}}}while(!st.empty()) {auto p=st.top();st.pop();Fork(i,p.fi.fi,p.fi.se) a[i]=p.se;}For(i,n) cout<<a[i]<<endl;return 0;
}B
给nnn个点对,每个点对(x,y)(x,y)(x,y)可以覆盖S=(a,b)∣b<=y,∣a−x∣<=y−bS={(a,b)|b<=y,|a-x|<=y-b}S=(a,b)∣b<=y,∣a−x∣<=y−b。问取多少个点对能覆盖所有点对。
经典题
#include<bits/stdc++.h>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define ForkD(i,k,n) for(int i=n;i>=k;i--)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=next[p])
#define Lson (o<<1)
#define Rson ((o<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,0x3f,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define MEMx(a,b) memset(a,b,sizeof(a));
#define INF (0x3f3f3f3f)
#define F (1000000007)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define vi vector<int>
#define pi pair<int,int>
#define SI(a) ((a).size())
#define Pr(kcase,ans) printf("Case #%d: %lld\n",kcase,ans);
#define PRi(a,n) For(i,n-1) cout<<a[i]<<' '; cout<<a[n]<<endl;
#define PRi2D(a,n,m) For(i,n) { \For(j,m-1) cout<<a[i][j]<<' ';\cout<<a[i][m]<<endl; \}
#pragma comment(linker, "/STACK:102400000,102400000")
#define ALL(x) (x).begin(),(x).end()
#define gmax(a,b) a=max(a,b);
#define gmin(a,b) a=min(a,b);
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
ll mul(ll a,ll b){return (a*b)%F;}
ll add(ll a,ll b){return (a+b)%F;}
ll sub(ll a,ll b){return ((a-b)%F+F)%F;}
void upd(ll &a,ll b){a=(a%F+b%F)%F;}
inline int read()
{int x=0,f=1; char ch=getchar();while(!isdigit(ch)) {if (ch=='-') f=-1; ch=getchar();}while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar();}return x*f;
}
int n;
vector<pair<int,int> > v;
int main()
{
// freopen("B.in","r",stdin);
// freopen(".out","w",stdout);int n=read();For(i,n) {int a=read(),b=read();v.pb(mp(b-a,a+b));}sort(ALL(v));stack<pair<int,int> > st; for(int i=0;i<n;i++) {auto now=v[i];while(!st.empty()){auto t=st.top();if(t.fi<=now.fi && t.se <=now.se) {st.pop(); }else break;}st.push(now);}cout<<SI(st)<<endl;return 0;
}C
考虑n*n的四连通矩阵,每次可以上下左右走一个。
格子上有颜色(黑、白),且只有白色能走。现在你希望令2个白色格子连通。一次操作为把n∗nn*nn∗n的矩阵赋值为白色。问至少几次操作实现目标。
#include<bits/stdc++.h>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define ForkD(i,k,n) for(int i=n;i>=k;i--)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=next[p])
#define Lson (o<<1)
#define Rson ((o<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,0x3f,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define MEMx(a,b) memset(a,b,sizeof(a));
#define INF (0x3f3f3f3f)
#define F (1000000007)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define vi vector<int>
#define pi pair<int,int>
#define SI(a) ((a).size())
#define Pr(kcase,ans) printf("Case #%d: %lld\n",kcase,ans);
#define PRi(a,n) For(i,n-1) cout<<a[i]<<' '; cout<<a[n]<<endl;
#define PRi2D(a,n,m) For(i,n) { \For(j,m-1) cout<<a[i][j]<<' ';\cout<<a[i][m]<<endl; \}
#pragma comment(linker, "/STACK:102400000,102400000")
#define ALL(x) (x).begin(),(x).end()
#define gmax(a,b) a=max(a,b);
#define gmin(a,b) a=min(a,b);
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
ll mul(ll a,ll b){return (a*b)%F;}
ll add(ll a,ll b){return (a+b)%F;}
ll sub(ll a,ll b){return ((a-b)%F+F)%F;}
void upd(ll &a,ll b){a=(a%F+b%F)%F;}
inline int read()
{int x=0,f=1; char ch=getchar();while(!isdigit(ch)) {if (ch=='-') f=-1; ch=getchar();}while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar();}return x*f;
}
int r,c,n,sx,sy,tx,ty;
int dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
bool inside(int x,int y) {return 1<=x && x<=r &&1<=y &&y<=c;
}
vector<string> a;
bool state(int x,int y){return a[x-1][y-1]=='#';
}
pair<int,int> dis[6000000+10];
int id(int x,int y) {return c*(x-1)+y;
}
void pri(pair<int,int> p) {printf("(%d,%d)",p.fi,p.se);
}
void pri(vector<pair<int,int> > v) {for(auto a:v) {pri(a);cout<<":";int x=a.fi,y=a.se;pri(dis[id(x,y)]);cout<<" ";}cout<<endl;
}
void bfs() {vector<pair<int,int> > q0,qa,qb;int nowdis=0;For(i,r*c) dis[i]=mp(INF,INF);dis[id(sx,sy)]=mp(0,n);q0.pb(mp(sx,sy));while(SI(q0)) {int nxdis=nowdis+1;// relax q0for(int i=0;i<SI(q0);i++) {auto t=q0[i];int x=t.fi,y=t.se;auto now_dis=dis[id(x,y)];Rep(di,4) {int nx=x+dir[di][0],ny=y+dir[di][1];if(!inside(nx,ny)) continue;if(dis[id(nx,ny)]!=mp(INF,INF)) continue;int sta=state(nx,ny);if(sta==0) { //whitedis[id(nx,ny)] = now_dis;q0.pb(mp(nx,ny));}}} // q0 -> qaRep(i,SI(q0)) {qa.pb(q0[i]);}Rep(i,SI(qa)) {auto t=qa[i];int x=t.fi,y=t.se;auto now_dis=dis[id(x,y)];Rep(di,2) {int nx=x+dir[di][0],ny=y+dir[di][1];if(!inside(nx,ny)) continue;if(dis[id(nx,ny)]!=mp(INF,INF)) continue;int sta=state(nx,ny);if(now_dis.fi==nowdis) {dis[id(nx,ny)] = mp(nxdis,1);}else if(now_dis.se+1<=n){dis[id(nx,ny)] = mp(nxdis,now_dis.se+1);}else continue;qa.pb(mp(nx,ny));}}//qa -> abRep(i,SI(qa)) {qb.pb(qa[i]);}Rep(i,SI(qb)) {auto t=qb[i];int x=t.fi,y=t.se;auto now_dis=dis[id(x,y)];Fork(di,2,3) {int nx=x+dir[di][0],ny=y+dir[di][1];if(!inside(nx,ny)) continue;if(dis[id(nx,ny)]!=mp(INF,INF)) continue;int sta=state(nx,ny);if(now_dis.fi==nowdis) {dis[id(nx,ny)]=mp(nxdis,n+1);}else if(now_dis.fi==nxdis && now_dis.se<n && n+1<=2*n ) {dis[id(nx,ny)]=mp(nxdis,n+1);}else if(now_dis.fi==nxdis && now_dis.se==n && n+2<=2*n ) {dis[id(nx,ny)]=mp(nxdis,n+2);}else if(now_dis.fi==nxdis && now_dis.se>n && now_dis.se+1<=2*n ) {dis[id(nx,ny)]=mp(nxdis,now_dis.se+1);}else continue;qb.pb(mp(nx,ny));}}
//
// cout<<nowdis<<endl;
// cout<<"q0"<<endl;
// pri(q0);
// cout<<"qa"<<endl;
// pri(qa);
// cout<<"qb"<<endl;
// pri(qb);
// //ab -> qc(q0)q0.resize(0);for(int i=0;i<qb.size();i++) {auto t=qb[i];int x=t.fi,y=t.se;auto now_dis=dis[id(x,y)];if(now_dis.fi==nxdis)q0.pb(qb[i]);}qa.resize(0),qb.resize(0);nowdis++;}
// For(i,r) {
// For(j,c) pri(dis[id(i,j)]),putchar(' ');
// puts("");
// }cout<<dis[id(tx,ty)].fi<<endl;}
int main()
{
// freopen("C.in","r",stdin);
// freopen(".out","w",stdout);cin>>r>>c>>n;
// For(i,r) For(j,c) cout<<id(i,j)<<' ';cin>>sx>>sy>>tx>>ty;For(i,r) {string s;cin>>s;a.pb(s);}bfs();return 0;
}D Cat Exercise
给一个nnn个节点的树,点权aia_iai。
执行如下操作:
- 选取点权最大的点
- 删除这个点及其相连的边,若有剩余连通块中取一个,跳回1。否则结束。
问操作1取的点权的和最大值。
相关文章:
 Final Round 题解)
The 22nd Japanese Olympiad in Informatics (JOI 2022/2023) Final Round 题解
交题:https://cms.ioi-jp.org/documentation A 给一个序列 a1,⋯,ana_1,\cdots,a_na1,⋯,an。 执行nnn个操作,第iii个操作为找出第iii个数前离其最近且与它相同的数的位置,把这两个数之间的数全部赋值aia_iai。求最后的序列。 考虑第…...

openEuler RISC-V 成功适配 VisionFive 2 单板计算机
近日,RISC-V SIG 成功在 VisionFive 2 开发板上适配欧拉操作系统,目前最新版本的 openEuler RISC-V 22.03 V2 镜像已在 VisionFive 2 开发板上可用,这是 openEuler 推动 RISC-V 生态演进的又一新进展。下载链接https://mirror.iscas.ac.c…...
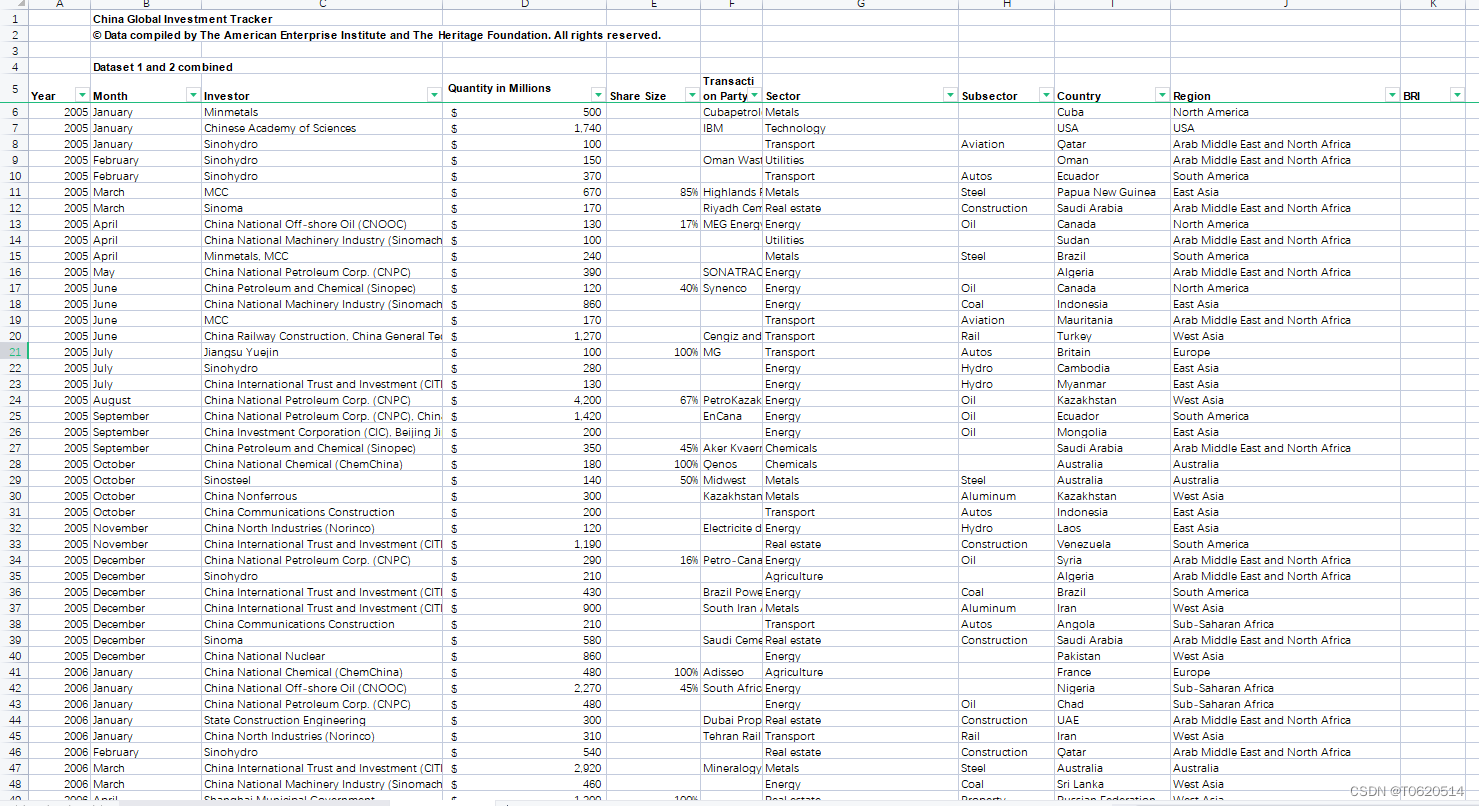
2005-2022中国企业对外直接投资、OFDI海外投资明细、中国全球投资追踪数据CGIT(含非建筑施工类问题投资)
中国全球投资跟踪”(China Global Investment Tracker),数据库,美国企业研究所于1月28日发布。数据库显示,2005年以来,中国对外投资和建设总额已接近2万亿美元。该数据库是唯一一套涵盖中国全球投资和建设的…...
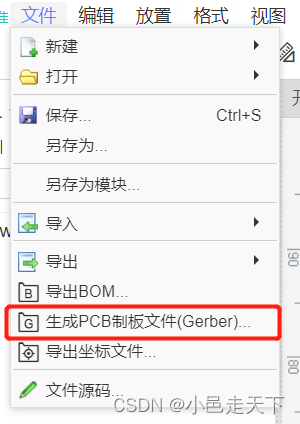
PCB学习笔记——使用嘉立创在线绘制原理图与PCB
嘉立创软件地址:https://lceda.cn/ 新建工程-新建原理图,在元件库中可以搜索元器件,可以直接放置在原理图上。 原理图绘制完成后,保存文件,设计-原理图转PCB,可以直接生成对应的PCB,设置边框&…...

【C++】类型转化
🌈欢迎来到C专栏~~类型转化 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤&…...

Mybatis -- resultMap以及分页
查询为null问题 要解决的问题:属性名和字段名不一致 环境:新建一个项目,将之前的项目拷贝过来 1、查看数据库的字段名 2、Java中的实体类设计 public class User { private int id; //id private String name; //姓名 private String passwo…...
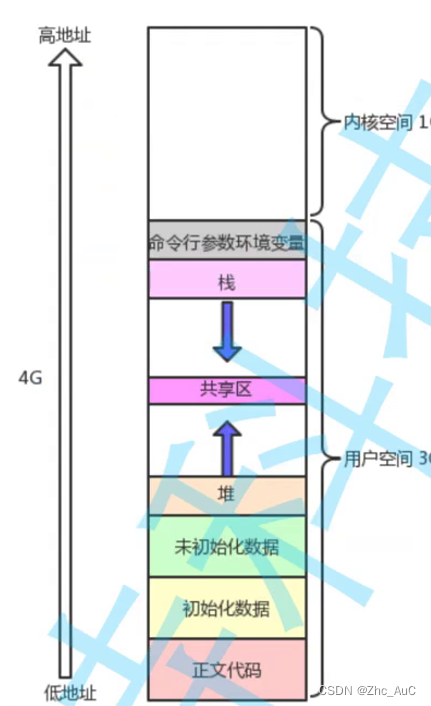
Linux之进程
一.冯诺依曼体系 在计算机中,CPU(中央处理器)是不直接跟外部设备直接进行通信的,因为CPU处理速度太快了,而设备的数据读取和输入有太慢,而是CPU以及外设直接跟存储器(内存)打交道&am…...

结构体——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容是结构体噢,之前我们在初始C语言中其实就已经学习过了结构体的知识,但是不是很全面,这次,我们也只是稍微详细一点,敬请期待小雅兰之后的博客ÿ…...

CCNP350-401学习笔记(51-100题)
51、Which statement about a fabric access point is true?A. It is in local mode and must be connected directly to the fabric edge switch. B. It is in local mode and must be connected directly to the fabric border node C. It is in FlexConnect mode and must …...
C语言学习_DAY_4_判断语句if_else和分支语句switch_case【C语言学习笔记】
高质量博主,点个关注不迷路🌸🌸🌸! 目录 1.案例引入 2.if判断语句的语法与注意事项 3.switch多分支语句的语法与注意事项 前言: 书接上回,我们已经学习了所有的数据类型、运算符,并且可以书写…...
)
实验07 赫夫曼编码及综合2022(带程序填空)
A. 【程序填空】赫夫曼编码题目描述给定n个叶子的权值,根据这些权值构造huffman树,并输出huffman编码参考课本第6.6节的算法6.12,注意算法中数组访问是从位置1开始赫夫曼构建中,默认左孩子权值不大于右孩子权值如果遇到两个孩子权…...
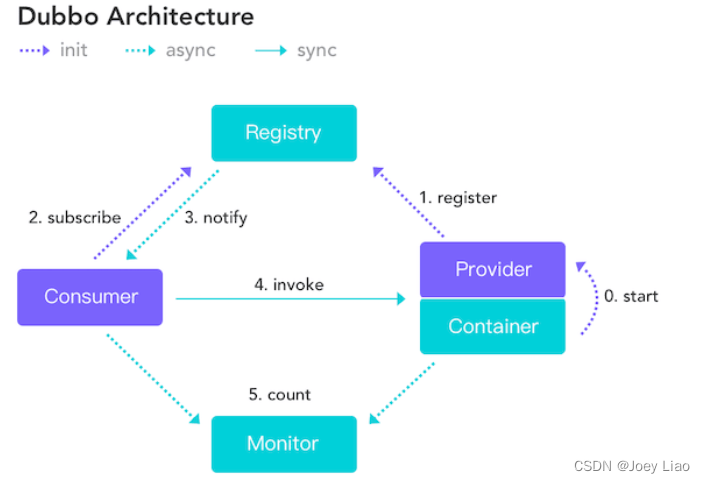
分布式 CAP BASE理论
文章目录CAP简介不是所谓的“3 选 2”CAP 实际应用案例BASE简介BASE 理论的核心思想总结CAP 简介 在理论计算机科学中,CAP 定理(CAP theorem)指出对于一个分布式系统来说,当设计读写操作时,只能同时满足以下三点中的…...

三调地类筛选器,Arcgis地类筛选
三调地类在使用是,需要分类统计,这个可以用于筛选; 标准地类筛选 农用地: DLBM IN(0303,0304,0306,0402,0101,0102,0103,0201,0201K,0202,0202K,0203,0203K,0204,0204K,0301,0301K,0302,0302K,0305,0307,0307K,0401,0403,0403K…...
)
华为OD机试 - 密室逃生游戏(Python)
密室逃生游戏 题目 小强增在参加《密室逃生》游戏,当前关卡要求找到符合给定 密码 K(升序的不重复小写字母组成) 的箱子, 并给出箱子编号,箱子编号为 1~N 。 每个箱子中都有一个 字符串 s ,字符串由大写字母、小写字母、数字、标点符号、空格组成, 需要在这些字符串中…...

白话C#之委托
一、什么是委托? 书本上是这样来定义委托的: 委托是一种动态调用方法的类型,属于引用型。委托是对方法的抽象和封装。委托对象实质上代表了方法的引用(即内存地址)。委托通常是委托某个方法来实现具体的功能。当我们调…...
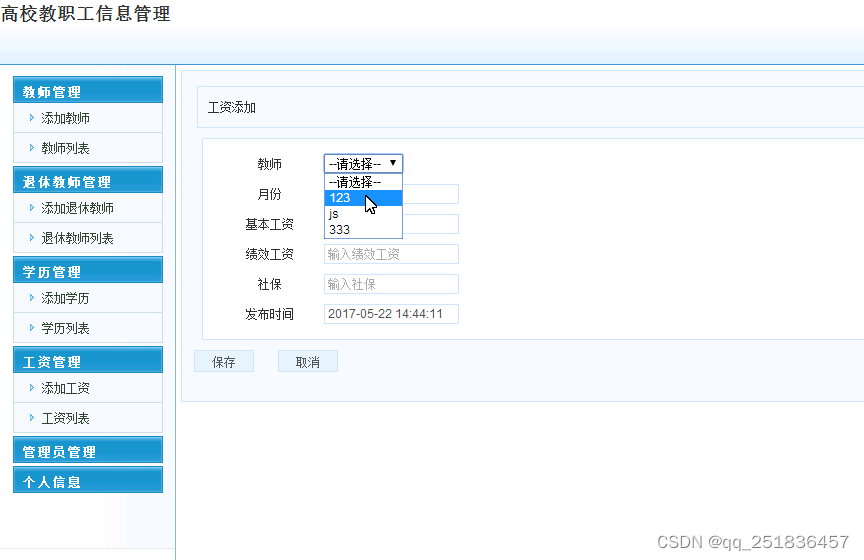
jsp高校教职工管理系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 jsp 高校教职工管理系统 是一套完善的web设计系统,对理解JSP java编程开发语言有帮助mvc模式 serlvetdaobean方式开发,系统具有完整的源代码和数据库,系统主要采用B/S模式 开发。开发环境为TOMCAT7.0,Myeclipse8.5开发&#…...

2023年数学建模美赛A题(A drought stricken plant communities)分析与编程
2023年数学建模美赛A题(A drought stricken plant communities)分析与编程 2023年数学建模美赛D题(Prioritizing the UN Sustainability Goals)分析与编程 特别提示: 1 本文介绍2023年美赛题目,进行深入分析…...

Delphi 中自定义鼠标指针图像
Dephi中的鼠标指针是可以自由定义的,如果是使用系统提供的图标,那么直接通过可视控件的Cursor属性赋值就可以。例如设置Form的鼠标为 crHourGlass 沙漏:Form1.Cursor : crHourGlass;也可以在设计期(IDE环境中)直接更改…...

【计算机网络】物理层
文章目录物理层的基本概念传输媒体同轴电缆双绞线光纤电力线电磁波红外线可见光传输方式串行传输和并行传输同步传输和异步传输单工,半双工以及全双工通信编码与调制常用编码不归零编码归零编码曼彻斯特编码差分曼彻斯特编码基本调制混合调制信道的极限容量奈氏准…...
)
华为OD机试 - 最少停车数(Python)
最少停车数 题目 特定大小的停车场 数组cars表示 其中1表示有车0表示没车 车辆大小不一,小车占一个车位(长度1) 货车占两个车位(长度2) 卡车占三个车位(长度3) 统计停车场最少可以停多少辆车 返回具体的数目 输入 整型字符串数组cars 其中1表示有车0表示没车 数组长度 <…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
