【每日一题Day122】LC1237找出给定方程的正整数解 | 双指针 二分查找
找出给定方程的正整数解【LC1237】
给你一个函数
f(x, y)和一个目标结果z,函数公式未知,请你计算方程f(x,y) == z所有可能的正整数 数对x和y。满足条件的结果数对可以按任意顺序返回。尽管函数的具体式子未知,但它是单调递增函数,也就是说:
f(x, y) < f(x + 1, y)f(x, y) < f(x, y + 1)函数接口定义如下:
interface CustomFunction { public:// Returns some positive integer f(x, y) for two positive integers x and y based on a formula.int f(int x, int y); };你的解决方案将按如下规则进行评判:
- 判题程序有一个由
CustomFunction的9种实现组成的列表,以及一种为特定的z生成所有有效数对的答案的方法。- 判题程序接受两个输入:
function_id(决定使用哪种实现测试你的代码)以及目标结果z。- 判题程序将会调用你实现的
findSolution并将你的结果与答案进行比较。- 如果你的结果与答案相符,那么解决方案将被视作正确答案,即
Accepted。
说真的 我看了评论区才看懂题目的
暴力
-
思路:双重循环枚举每个可能的xxx和yyy,通过
customfunction.f(x, y)求出运算结果,如果结果等于zzz,那么加入结果集中;由于函数是单调递增函数,因此如果结果大于zzz时,退出循环。 -
实现
class Solution {public List<List<Integer>> findSolution(CustomFunction customfunction, int z) {List<List<Integer>> res = new ArrayList<>();for (int i = 1; i <= 1000; i++){for (int j = 1; j <= 1000; j++){int num = customfunction.f(i, j);if (num == z){res.add(Arrays.asList(i, j));}else if (num > z){break;}}}return res;} }-
复杂度
- 时间复杂度:O(C2)O(C^2)O(C2),CCC为x和y的取值范围,本题中为100010001000
- 空间复杂度:O(1)O(1)O(1)
-
二分查找
-
思路:由于函数为单调递增函数,因此可以固定xxx,二分查找yyy,二分查找的上限为1,下限为1000,假定运算结果为numnumnum
- 如果num==znum==znum==z,那么将结果添加至结果集
- 如果num>znum>znum>z,那么yyy向左边查询,right = mid - 1
- 如果num==znum==znum==z,那么yyy向右边查询,left = mid + 1
-
实现
/** // This is the custom function interface.* // You should not implement it, or speculate about its implementation* class CustomFunction {* // Returns f(x, y) for any given positive integers x and y.* // Note that f(x, y) is increasing with respect to both x and y.* // i.e. f(x, y) < f(x + 1, y), f(x, y) < f(x, y + 1)* public int f(int x, int y);* };*/class Solution {public List<List<Integer>> findSolution(CustomFunction customfunction, int z) {List<List<Integer>> res = new ArrayList<>();for (int i = 1; i <= 1000; i++){int jL = 1, jR = 1000;while (jL <= jR){int mid = (jL + jR) / 2;int num = customfunction.f(i, mid);if (num == z){res.add(Arrays.asList(i, mid));break;}else if (num > z){jR = mid - 1;}else{jL = mid + 1;}}}return res;} }-
复杂度
- 时间复杂度:O(ClogC)O(ClogC)O(ClogC),CCC为x和y的取值范围,本题中为100010001000
- 空间复杂度:$O(1) $
-
双指针
-
思路:当x1<x2x_1<x_2x1<x2时,如果f(x1,y1)=f(x2,y2)=zf(x_1,y_1)=f(x_2,y_2)=zf(x1,y1)=f(x2,y2)=z,那么此时y1>y2y_1>y_2y1>y2,因此可以从小到大枚举xxx,从大到小枚举yyy,那么可以固定xxx,在上次循环的yyy值作为起始值,找到本次的yyy。
-
实现
class Solution {public List<List<Integer>> findSolution(CustomFunction customfunction, int z) {List<List<Integer>> res = new ArrayList<>();int j = 1000;for (int i = 1; i <= 1000; i++){while (j >= 1 && customfunction.f(i, j) > z){j--;}if (j >= 1 && customfunction.f(i, j) == z){res.add(Arrays.asList(i, j));}}return res;} }-
复杂度
- 时间复杂度:O(C)O(C)O(C),CCC为x和y的取值范围,本题中为100010001000
- 空间复杂度:$O(1) $
-
相关文章:

【每日一题Day122】LC1237找出给定方程的正整数解 | 双指针 二分查找
找出给定方程的正整数解【LC1237】 给你一个函数 f(x, y) 和一个目标结果 z,函数公式未知,请你计算方程 f(x,y) z 所有可能的正整数 数对 x 和 y。满足条件的结果数对可以按任意顺序返回。 尽管函数的具体式子未知,但它是单调递增函数&#…...
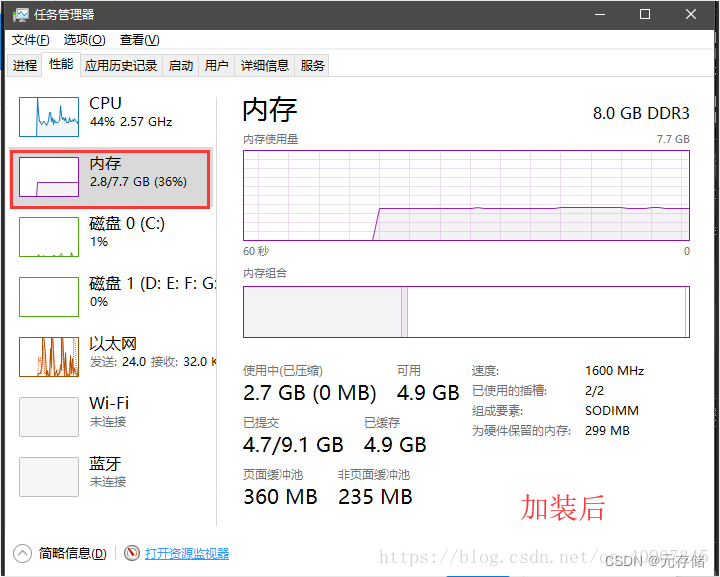
笔记本加装固态和内存条教程(超详细)
由于笔记本是几年前买的了,当时是4000,现在用起来感到卡顿,启动、运行速度特别慢,就决定换个固态硬盘,加个内存条,再给笔记本续命几年。先说一下加固态硬盘SSD的好处:1.启动快 2.读取延迟小 3.写…...

【Python】字典 - Dictionary
字典 - Dictionarykeys()values()items()get()获取文件中指定字符的个数进阶版:获取所有单词的频数进阶版:获取所有字符的频数函数内容keys()输出字典中的所有键values()输出字典中的所有值items()以元组的形式输出键值对get()获取字典中指定键的值 keys…...
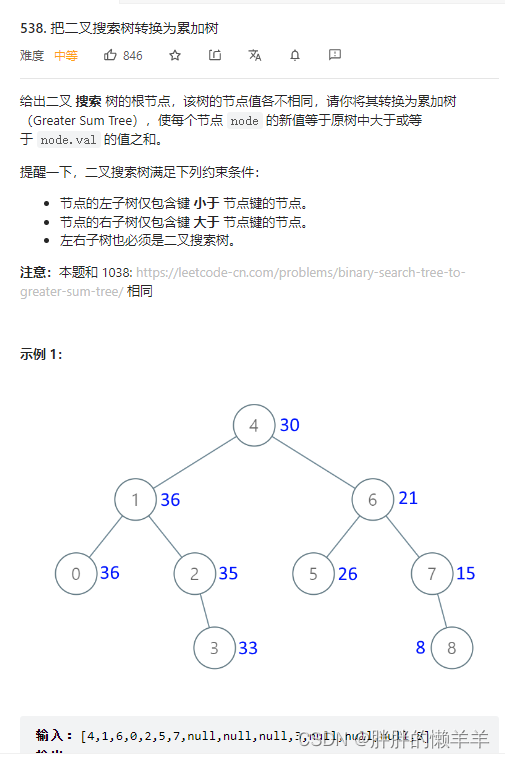
LeetCode分类刷题----二叉树
二叉树1.二叉树的递归遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历2.二叉树的迭代遍历144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历3.二叉树的层序遍历102.二叉树的层序遍历107.二叉树的层序遍历||199.二叉树的右视图637.二叉树的层平均…...
)
Zipkin : Golang 微服务全链路监控(三)
Zipkin : Golang 微服务全链路监控(三) Golang 微服务全链路监控实现 broker-service -> auth-service -> postgres dbzipkin 监控:需代码入侵 使用 zipkin 库的 serverMiddleware,其通过 Http 跟踪(trace&am…...
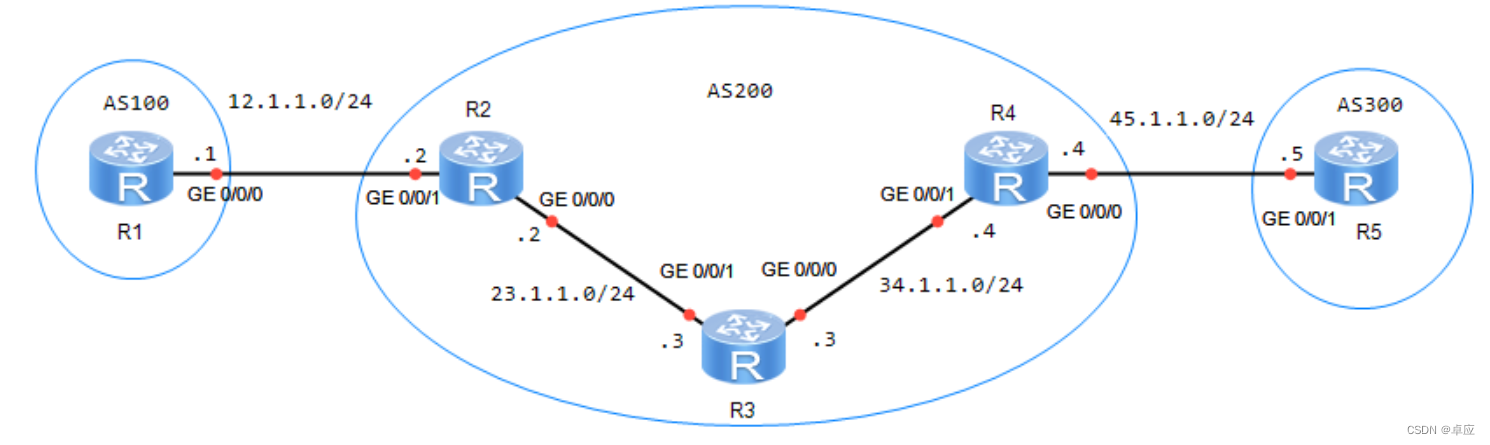
5.3 BGP路由黑洞
5.2.3实验3:BGP路由黑洞 1. 实验目的 熟悉BGP路由黑洞的应用场景掌握BGP水平分割的配置方法2. 实验拓扑 实验拓扑如图5-3所示: 图5-3:BGP路由黑洞 3. 实验步骤 配置IP地址 R1的配置 <Huawei>syst...
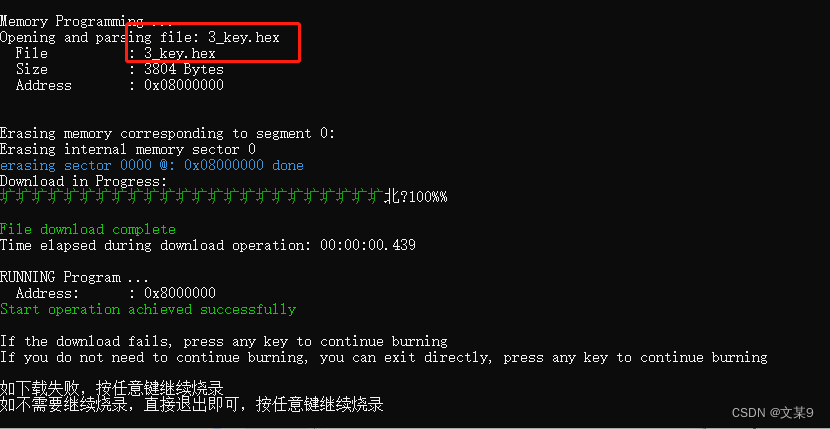
STM32 DFU模式烧录代码
什么是DFU? dfu的本质是isp,usb接口的isp,在系统编程,进入isp的方式我们先了解 如下图 boot0为高电平 boot1为低电平即可进入isp模式。 熟悉的场景 在我们使用flymcu软件下载代码时,本质也是isp 串口接口的isp。 傻瓜使用方式…...
松下PLC通过fpwin上传写入MRTC模块方法
目录 PLC程序上传方法 加密模块使用 PLC程序上传方法 手动将PLC模式设置为prog模式查看PLC是否设置为禁止上传查询指示灯是否变蓝,变蓝则需要将PLC禁止上传功能取消。 3.当上述动作操作完成后,将PLC程序导入到PLC中。为了配合加密程序使用,…...

就业大山之下的网络安全:安逸的安服仔
从去年开始,各个互联网大厂就接二连三的放出了裁员消息,整个互联网行业好像都处于寒冬状态。微博、小米、滴滴、知乎、拼多多等在内的一大批互联网知名企业,也相继传出“人员优化”的消息。 除了国内市场的萧条,国外市场也是不容…...
JavaWeb3-线程的3种创建方式7种写法
目录 1.方式一:继承Thread(2种写法) 写法①(常规): a.使用jconsole观察线程 b.启动线程——start方法 PS:(常见面试题)start 方法与 run 方法的区别: 写…...

驱动调试手段
文章目录 前言一、通过sysfs调试LCD查看电源:查看 pwm 信息查看管脚信息总结前言 本文记录在驱动中常用的调试手段 提示:以下是本篇文章正文内容,下面案例可供参考 一、通过sysfs 系统起来之后可以读取 sysfs 一些信息,来协助调试 示例: 调试LCD 输入如下命令 cat /…...

[RK3568 Android12] 音频及路由
1:概述(耳机 ,hdmiin ,板载喇叭) 在开发板上面,系统注册了三个音频输出通道,如下: [ 2.280612] ALSA device list: [ 2.280622] #0: rockchip,rk809-codec [ 2.280630] #1: ROCKCHIP,SPDIF [ 2.280638] #2: rockchip,hdmi console:/proc/asound # cat pcm …...

C++——C++11 第一篇
目录 统一的列表初始化 {}初始化 decltype 编辑 nullptr STL中一些变化 右值引用和移动语义 左值引用和右值引用 总结 左值引用优缺点 右值引用(将亡值) 拷贝赋值和移动赋值 万能引用|完美转发 移动构造和移动赋值注意…...
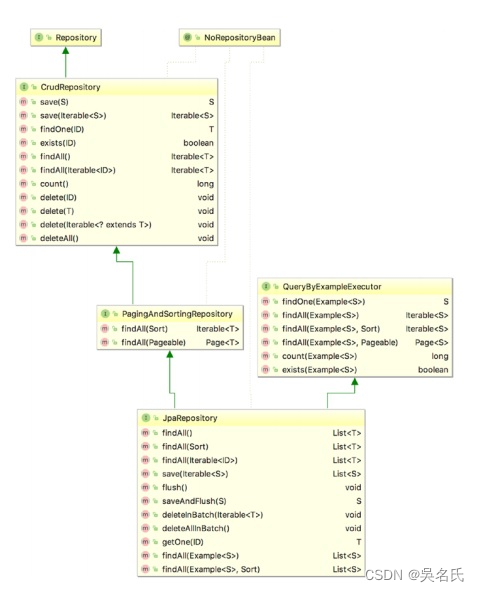
Spring Data JPA 中 CrudRepository 和 JpaRepository 的区别
1 问题描述Spring Data JPA 中,CrudRepository 和 JpaRepository 有何区别?当我在网上找例子的时候,发现它们可以互相替换使用。它们有什么不同呢?为什么你习惯用其中的一个而不是另一个呢?2 CrudRepository 和 JpaRep…...

推荐几款好用的数据库管理工具
本文主要介绍几款常用的数据库管理软件(客户端),包括开源/免费的、商用收费的,其中有一些是专用于 MySQL 数据库的,例如 MySQL Workbench、phpMyAdmin,有一些是支持多种 SQL、NoSQL 数据库的,例…...

DPDK — 性能优化手段
目录 文章目录 目录硬件布局层面的优化操作系统层面的优化Linux 操作系统版本应用程序层面的优化Cache 优化内存对齐内存预取SIMD 报文批处理DDIO使用高级 CPU 指令集硬件布局层面的优化 DPDK 在硬件布局层面的优化,主要体现在以下几个方面: CPU 频率的高低:CPU 频率越高,…...

Fedora Linux未来五年规划
Fedora 委员会一直致力于起草战略计划,以帮助 Fedora Linux 更好地发展。近日 Fedora 委员会公布了一份 “《未来五年的 Fedora Linux 》” 战略计划草案,这份草案里面包含了他们的雄心壮志:每周将 Fedora 的活跃贡献者人数增加一倍。 Fedora…...
【C++之容器篇】map和set常见函数接口的使用与剖析
目录前言一、set1. 简介2. 成员类型3. 构造函数(1) set()(2)set(InputIterator first,InputIterator last)(3)使用4. 拷贝构造函数和赋值运算符重载5. empty()6. size()7. insert()(1)pair<iterator,bool> insert(const K& key)(2)iterator insert(iterator pos,cons…...
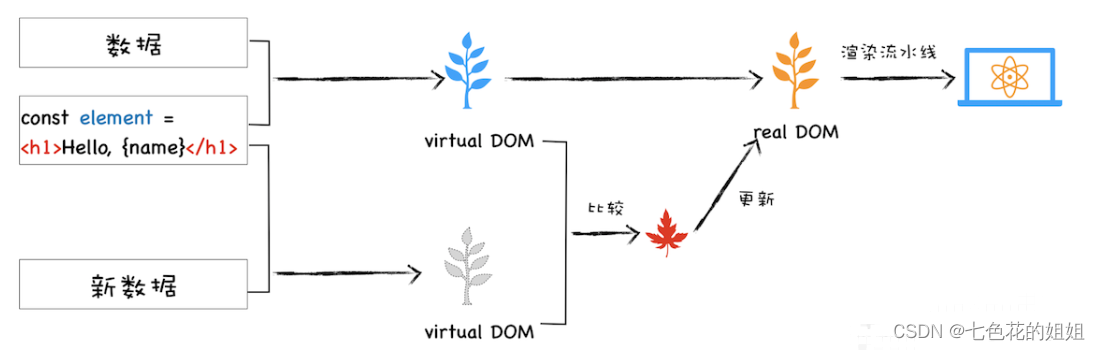
虚拟DOM是什么
参考文章做的总结,如有不足之处请指正! 在讲虚拟dom之前,先讲讲,为什么前端操作dom会导致页面性能降低? 先说几个概念 有助于后面的理解 什么是 JavaScript 引擎? JavaScript引擎是一个专门处理JavaScript脚…...
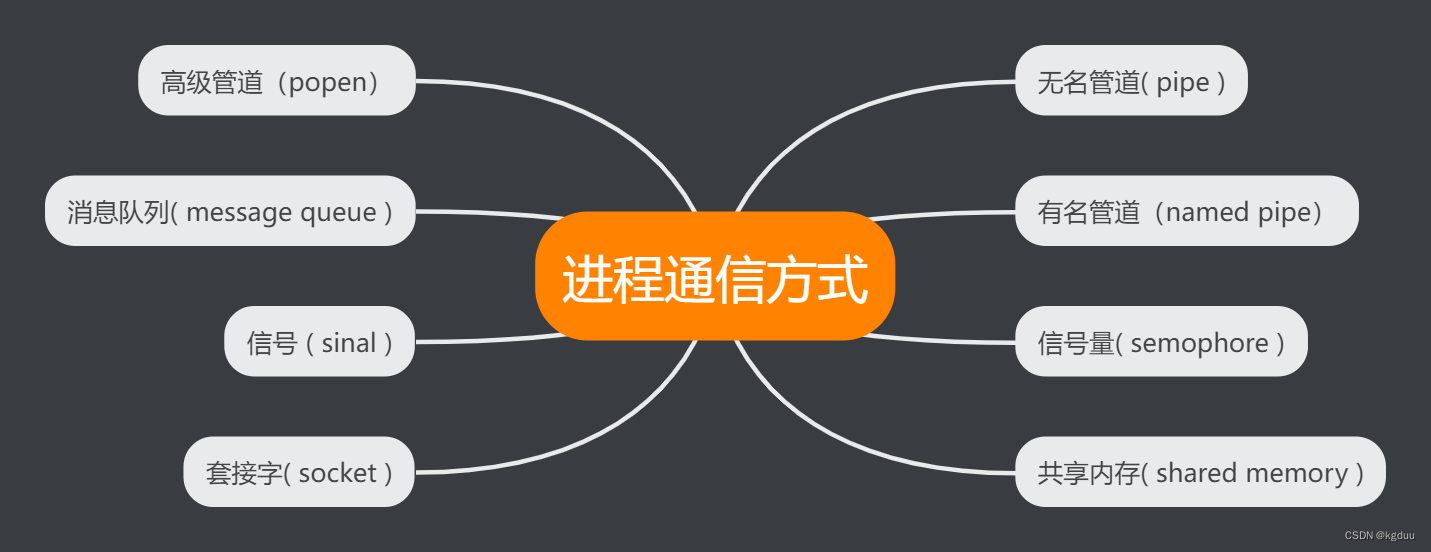
进程通信方式
无名管道( pipe ): 管道是一种半双工的通信方式,数据只能单向流动,而且只能在具有亲缘关系的进程间使用。进程的亲缘关系通常是指父子进程关系。高级管道(popen): 将另一个程序当做一个新的进程在当前程序进…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...
