剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
摘要
剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
一、双指针解析
考虑定义双指针 i , j分列数组左右两端,循环执行:
- 指针 i从左向右寻找偶数;
- 指针 j从右向左寻找奇数;
- 将偶数nums[i]和奇数 nums[j]交换。
可始终保证:指针 i左边都是奇数,指针j右边都是偶数 。
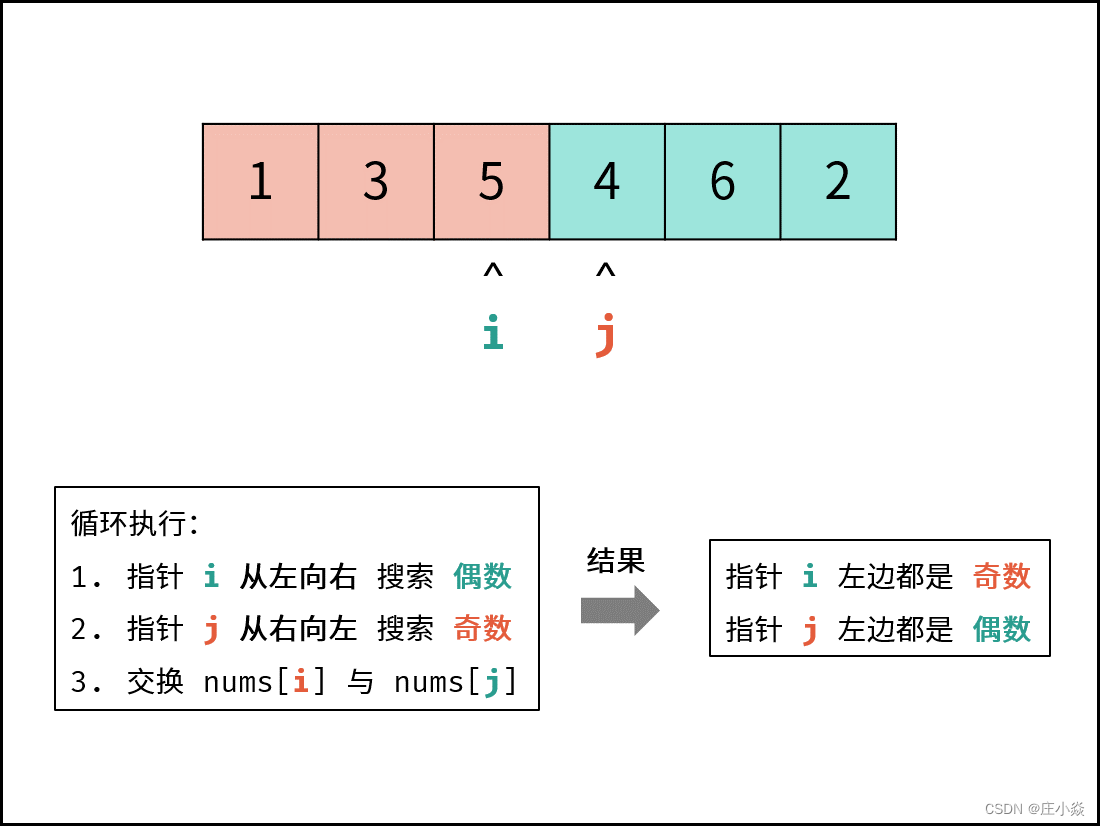
算法流程:
- 初始化:i, j双指针,分别指向数组 nums左右两端;
- 循环交换: 当 i=j时跳出;
- 指针i遇到奇数则执行 i=i+1跳过,直到找到偶数;
- 指针j遇到偶数则执行 j=j−1跳过,直到找到奇数;
- 交换 nums[i]和 nums[j]值;
- 返回值:返回已修改的 nums数组
class Solution {public int[] exchange(int[] nums) {int left = 0, right = nums.length - 1;while (left < right) {while (left < right && nums[left] % 2 == 1) {left++;}while (left < right && nums[right] % 2 == 0) {right--;}if (left < right) {int temp = nums[left];nums[left] = nums[right];nums[right] = temp;left++;right--;}}return nums;}
}复杂度分析:
- 时间复杂度 O(N): N为数组 nums长度,双指针 i, j共同遍历整个数组。
- 空间复杂度 O(1) : 双指针i, j使用常数大小的额外空间。
博文参考
《leetcode》
相关文章:

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
摘要 剑指 Offer 21. 调整数组顺序使奇数位于偶数前面 一、双指针解析 考虑定义双指针 i , j分列数组左右两端,循环执行: 指针 i从左向右寻找偶数;指针 j从右向左寻找奇数;将偶数nums[i]和奇数 nums[j]交换。 可始终保证&…...
实用版ChatBing论文阅读助手教程+新测评
实用版ChatBing论文阅读助手新测评 AI进化(更新)的速度太快了!距离我上次的【Chat嘴硬!基于NewBing的论文调研评测报告】,才四天,它已经进化到快能用的地步了! 这次是我刷B站看到热门推荐&…...
Linux生产者消费模型
1.生产者消费者模型 1.1 为何要使用生产者消费者模型 生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题。生产者和消费者彼此之间不直接通讯,而通过阻塞队列来进行通讯,所以生产者生产完数据之后不用等待消费者处理,直接…...
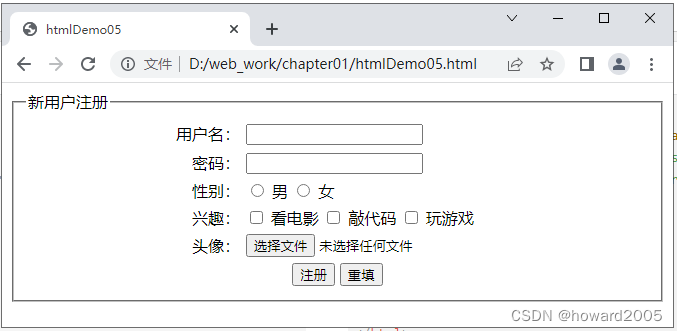
动态网站开发讲课笔记01:网页开发基础
文章目录零、本讲学习目标一、HTML基础(一)HTML简介1、HTML2、HTML语言的基本格式3、<!DOCTYPE>声明4、html标签5、head标签6、body标签7、编写第一个网页8、关于编写HTML文件的工具9、HTML标签概述(1)单标签(2&…...

互联网新时代要到来了(三)什么是ChatGPT?
什么是ChatGPT? tips:资料来自百度百科、openAi、CSDN博主「琦在江湖飘」、Info写作社区、CSDN博主「夕小瑶」等网页资料。 1.什么是ChatGPT? ChatGPT(全名:Chat Generative Pre-trained Transformer),…...
)
华为OD机试 - 环中最长子串(Python)
环中最长子串 题目 给你一个字符串s,首尾相连成一个环形, 请你在环中找出o字符出现了偶数次最长子字符串的长度. 备注: 1 <= s.lenth <= 5x10^5 s只包含小写英文字母 输入 输入是一个小写字母组成的字符串 输出描述 输出是一个整数 示例一 输入 alolobo输出 6说…...
安全—08day
ApabilitiesapabilitiesLinux Capabilities线程的 capabilitiesPermitted 允许Effective 有效InheritableBoundingAmbient文件的 capabilitiesPermittedInheritableEffective运行 execve() 后 capabilities 的变化案例分析方法一、依次执行如下命令方法二、iptables端口转发方案…...

【看表情包学Linux】进程地址空间 | 区域和页表 | 虚拟地址空间 | 初识写时拷贝
🤣 爆笑教程 👉 《看表情包学Linux》👈 猛戳订阅 🔥 💭 写在前面:本章核心主题为 "进程地址空间",会通过验证 Linux 进程的地址空间来开头,抛出 "同一个值能有不同内…...

响应式编程(Reactive Programming)介绍
什么是响应式编程? 在互联网上有着一大堆糟糕的解释与定义。Wikipedia 一如既往的空泛与理论化。Stackoverflow 的权威答案明显不适合初学者。Reactive Manifesto 看起来是你展示给你公司的项目经理或者老板们看的东西。微软的 Rx terminology"Rx Observables LINQ S…...

你不知道的美化列表的两种方案-<ul/><ol/>
大家好,我是半夏👴,一个励志更文1000篇沙雕程序员.如果喜欢我的文章,可以关注➕ 点赞 一起学习交流前端,成为更优秀的工程师~ CSS为什么这么难学?一定是你方法不对!!! 只要一杯奶茶,CSS任你学。学透CSS,拒绝切图仔!!! 学透CSS传送门 文章目录 学透CSS传送门前言li…...

2023年浙江理工大学MBA招生考试初试成绩查询及复查的通知
根据往年的情况,2023浙江理工大学MBA考试初试成绩可能将于2月21日下午两点公布,为了广大考生可以及时查询到自己的分数,杭州达立易考教育为大家汇总了信息。 一、成绩查询考生可登录中国研究生招生信息网“全国硕士研究生招生考试初试成绩查询…...
SVNH数据(.mat格式)转为图像(.png)matlab代码
一、获取SVNH数据数据集集地址-http://ufldl.stanford.edu/housenumbers/提供两种格式的数据:1.Format 1,图像形式,压缩包2.Format 2, .mat格式的数据10 classes, 1 for each digit. Digit 1 has label 1, 9 has label 9 and 0 ha…...

【总结】vim教程与详细命令总结,该来的躲不掉啊晕
B站|公众号:啥都会一点的研究生 目录写在前面vim的工作模式普通模式编辑模式命令模式命令大全,最详细(建议收藏)光标的移动插入模式 - 插入/追加文本编辑文本选择文本(可视化模式)可视化模式命令剪切, 复制…...
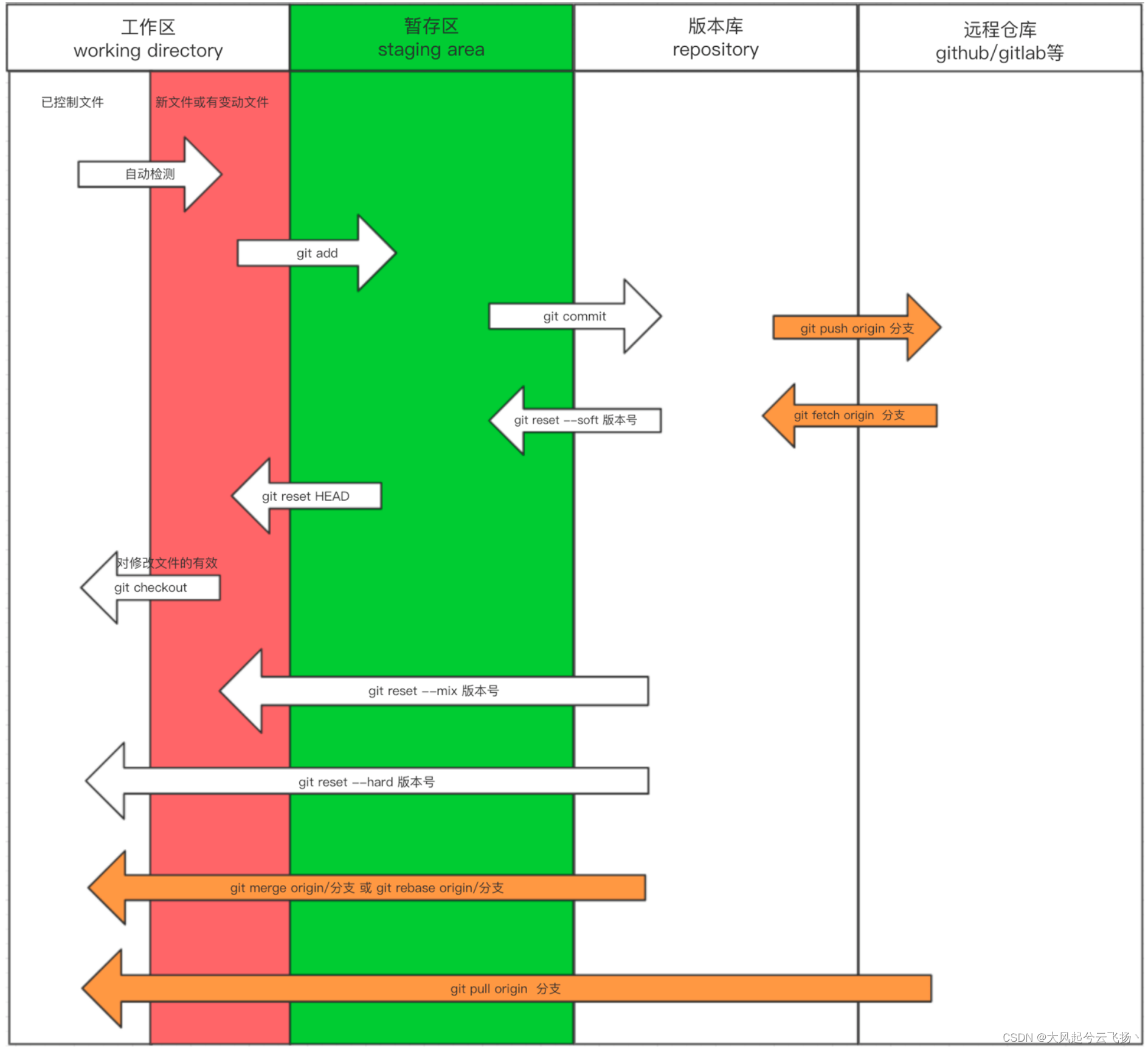
git基础使用
Git安装 去安装>> 正式开始 进入要管理的目录,执行命令 git init 查看管理目录下的状态 git status 注:新增文件和修改过后的文件都是红色 管理指定文件(红变绿) 指定文件:git add 文件名 当前目录下所有&…...

基于 RANSAC 的地面分割与聚类算法
文章目录 前言 一、算法原理 参考文献 二、代码实现 1.头文件 2.源文件...
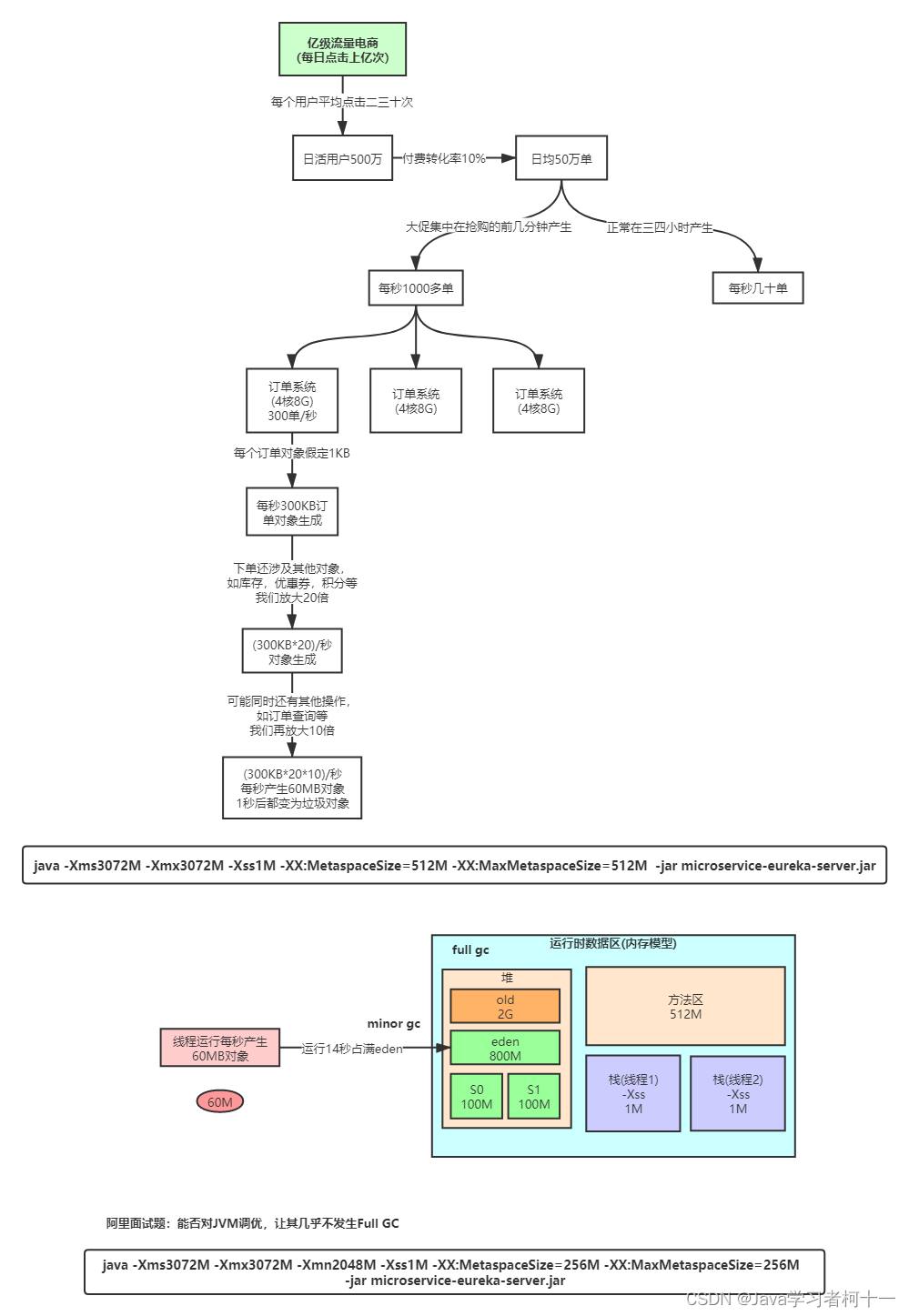
JVM内存模型深度剖析与优化
1. Java语言的跨平台特性 2. JVM整体结构及内存模型 堆存放着对象信息每个线程都会分配一块属于自己的内存空间(栈空间) 每个方法都会分配一块内存空间(栈桢),上图 compute()方法 和 main()方法 都会分配到各自的栈桢空…...

软件性能测试定义中文
From Wiki软件性能测试在软件质量保证中,性能测试通常是一种测试实践,用于确定系统在特定工作负载下的响应能力和稳定性方面的表现。它还可以用于调查、测量、验证或验证系统的其他质量 属性,例如可扩展性、可靠性和资源使用。性能测试是性能…...

2023情人节正经性生活调研报告
省时查报告-专业、及时、全面的行研报告库省时查方案-专业、及时、全面的营销策划方案库【免费下载】2023年1月份热门报告合集ChatGPT的发展历程、原理、技术架构及未来方向2023年,如何科学制定年度规划?《底层逻辑》高清配图今天给大家带来丁香医生最新…...

22- 隐马尔科夫HMM (NLP自然语言算法) (算法)
HMM模型 : from hmmlearn.hmm import GaussianHMM model GaussianHMM(n_components3,n_iter100000, covariance_type diag) model.fit(X) 1、马尔科夫链 有向图模型(贝叶斯网络):用有向图表示变量间的依赖关系; 无向图模型&…...

gRPC是什么,怎么用
RPC是什么 RPC是指远程过程调用,也就是说两台服务器A,B,一个应用部署在A服务器上,想要调用B服务器上应用提供的函数/方法,由于不在一个内存空间,不能直接调用,需要通过网络来表达调用的语义和传…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
